压电圆环晶片堆的径向振动分析
- 格式:pdf
- 大小:356.96 KB
- 文档页数:5
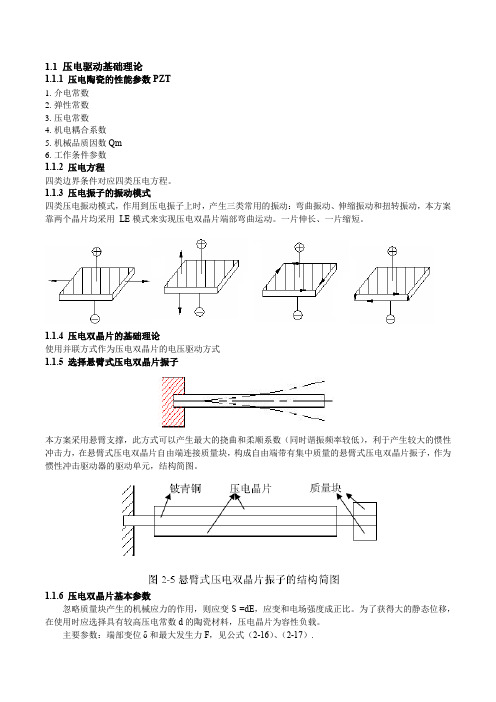

压电晶片工作原理压电晶片是一种应变敏感的材料,它能将机械能转化为电能,同时也能将电能转化为机械能。
其主要工作原理是基于压电效应和反压电效应。
压电效应指的是某些晶体材料在外部施加应力时,产生电荷极化现象。
这种材料称为压电材料。
常见的压电材料有石英、岩石陶瓷和固体聚合物等。
在压电晶片中,通常使用的是压电陶瓷材料,如铅锆钛酸钪(PZT)。
压电效应的原理可以通过晶格结构进行解释。
在没有应力作用时,压电晶片的晶格处于对称无序状态,正负电荷呈均匀分布。
当外部施加应力时,晶格结构发生畸变,导致正负电荷不再均匀分布,而是趋向于聚集在压力的一侧或拉伸的一侧。
这样就形成了一个电荷极化矢量,即电偶极矩。
当应力解除时,晶格恢复对称无序状态,电荷分布也恢复均匀,这个过程称为反压电效应。
在正压作用下,压电晶片的正压面上会产生正电荷,而负压面上会产生负电荷。
这种正负电荷的不对称分布会引起电势差,即产生电压。
如果将两个电极连接到压电晶片的两个面上,就可以测量到电荷的变化。
压电晶片还可以通过逆向作用,即电能转化为机械能。
当外部电场施加到压电晶片上时,由于电场的作用,晶体会发生电荷重排,导致压电晶片的尺寸变化。
这种尺寸变化可以作用于机械装置,例如振动器、压电陶瓷的振动支座或驱动器等。
这样,压电晶片就能将电能转化为机械能。
逆压电效应是压电晶片在声学、声纳、振动发生器等领域应用的基础。
总体而言,压电晶片的工作原理是基于压电效应和反压电效应。
通过施加或施加到压电晶片上的应力或电场,可以在晶片中产生电荷分布的不对称性,从而形成电势差或引起尺寸变化。
这种能够相互转换机械能和电能的特性,使得压电晶片在传感、驱动和控制等领域有着广泛的应用。

( 实验报告)姓名:____________________单位:____________________日期:____________________编号:YB-BH-004578压电式传感器测振动实验报告Experimental report on vibration measurement with piezoelectric压电式传感器测振动实验报告一、实验目的:了解压电传感器的测量振动的原理和方法。
二、基本原理:压电式传感器由惯性质量块和受压的压电片等组成。
(观察实验用压电加速度计结构)工作时传感器感受与试件相同频率的振动,质量块便有正比于加速度的交变力作用在晶片上,由于压电效应,压电晶片上产生正比于运动加速度的表面电荷。
三、需用器件与单元:振动台、压电传感器、检波、移相、低通滤波器模板、压电式传感器实验模板。
双踪示波器。
四、实验步骤:1、压电传感器装在振动台面上。
2、将低频振荡器信号接入到台面三源板振动源的激励源插孔。
3、将压电传感器输出两端插入到压电传感器实验模板两输入端,与传感器外壳相连的接线端接地,另一端接R1。
将压电传感器实验模板电路输出端Vo1,接R6。
将压电传感器实验模板电路输出端V02,接入低通滤波器输入端Vi,低通滤波器输出V0与示波器相连。
3、合上主控箱电源开关,调节低频振荡器的频率和幅度旋钮使振动台振动,观察示波器波形。
4、改变低频振荡器的频率,观察输出波形变化。
光纤式传感器测量振动实验一、实训目的:了解光纤传感器动态位移性能。
二、实训仪器:光纤位移传感器、光纤位移传感器实验模块、振动源、低频振荡器、通信接口(含上位机软件)。
三、相关原理:利用光纤位移传感器的位移特性和其较高的频率响应,用合适的测量电路即可测量振动。
四、实训内容与操作步骤1、光纤位移传感器安装如图所示,光纤探头对准振动平台的反射面,并避开振动平台中间孔。
2、根据“光纤传感器位移特性试验”的结果,找出线性段的中点,通过调节安装支架高度将光纤探头与振动台台面的距离调整在线性段中点(大致目测)。

压电材料的参数及压电方程一、压电方程对于压电材料的性能,我们有以下四个方面的考虑:1、压电材料是弹性体,它在力学效应上服从胡克定律,即应力τ和应变e之间服从弹性关系:τ=ce或e=sτ式中c为弹性模量,又称弹性刚度常数或弹性劲度常数,表示物体产生单位应变所需的力;s为弹性顺从系数,又称弹性柔顺常数,表示材料的应力与应变之间的关系并且s=1/c上述关系式的物理意义是:在弹性限度内,弹性体的应力与应变成正比。
2、压电材料是铁电体,它在电学效应中,其电学参数-电场强度E和电位移强度D之间服从介电关系式:E=βD或D=εE,式中ε为电容率,又称介电常数(单位:法/米),它反映材料的介电性质,对压电体则反映其极化性质,与压电体附上电极所构成的电容有关,即电容C=εA/t,式中A为两极板相对面积,t为两极间距离或者说是压电晶片的厚度,因而与压电体的电阻抗有关。
介电常数ε常用相对介电常数εr表示,其值等于同样电极情况下介质电容与真空电容之比:εr=C介/C真空=ε介/ε真空(ε真空=8.85x10-2法/米)β为介电诱导系数,又称介电隔离率,它表示电介质的电场随电位移矢量变化的快慢,并且β=1/ε,不过这个系数一般较少使用。
上述介电关系式的物理意义就是:当一个电介质处于电场E中时,电介质内部的电场可以用电位移D表示。
3、压电材料在磁学效应中有:B=μH,式中B为磁感应强度,H为磁场强度,μ为磁导率4、压电材料在热学效应中有:Q=φσ/ρc,式中Q为热量;φ为温度;σ为熵;ρ为介质密度;c为材料比热。
对于压电体,我们通常不考虑磁学效应并且认为在压电效应过程中无热交换(当然这并不确实,而仅仅是在简化分析时略去这两方面)。
因此,一般只考虑前面所述的力学效应和电学效应,而且还必须同时考虑它们之间存在的相互作用。
把两个力学量--应力τ和应变e与两个电学量--电场强度E和电位移强度D联系在一起,描述它们之间相互作用的表达式就是所谓的压电方程。

压电陶瓷薄圆片振子的厚度剪切振动第16卷第堋199d年1月压电与&声光voL16No.2AprilI994压电陶瓷薄圆片振子的厚度剪切振动林书玉(陕西师范丈学应用声学研究所.西安.?10063)1m1一擒耍本文研兜了切向极化压电陶瓷薄图片的厚度剪切振动.即扭转振动.利用压电方程及运动方程.推出了振子的机电等效电路.得出了振子扭转振动的输入电阻抗.并推出了其共振及反共振掇率方程.由于振子的扭转振动与其截面形状有关.因此.本文提出了振子的截面扭转系数的概念.并给出了实心及空心圜盘的截面扭转系数.本文理论对于扭转振动换能器设计理论的研兜.以及压电陶瓷振子振动模式的系列研兜具有一定的指导意义.关蕾调厚度剪切振动,扭转振动.截面扭转系数.压电陶瓷一-———一___——一—一,'ThicknessShearVibrationofPiezoelectricCeramicThinDiscsLtnshuyu(InApplkd^∞?ShaanxlTcmmUnlvendty?710063?且n)AIMm.actInthisp.1pH.b_shear60Il0rtors~lv/bat.ionofp~zoelectrieceramicthindj0∞was雠I坩i0d.Basedonthepiezoeleel~iCandwaveequati(ms?1heek吐rcm咖I.ica1equivalentc/rcuRand1hereoIIanceandfe9onancefzeq~encyequatlort~welederived-andtheinputelectricimped ancewa3ob-mined.11皓conceptofcn嘴}洲0ntoc~onalcoefficientwasintroducedandthef嚣ul蚀ofcircularandannu-tarcr衄轴cIion鼻wefegiven-Theth∞fy/sofcertain哪nirI|州n憾fortd曙ignofto~onalt埔nsdIIc啪andthestudyofV胁b∞mode.er妇ofpiezoelectricoeratTIicvibra~ms. KeywordsthicknessSlllt~ffvibration.onaIvibration?cram-sectionto~ionaJcoefficient.p/ ezoelecu'icceramics1引言压电陶瓷振子是超声换能器,陶瓷滤波器,压电传感器,压电陀螺等器件的主要组成部分,而关于压电陶瓷振子振动模式的研究则是设计这些器件的理论基础.压电陶瓷振子的振动模式很多,其中包括伸缩振动模式本文1993年12月27日收到以及剪切振动模式等.关于振子的伸缩振动模式以及矩形振子的厚度剪切振动,已经有了比较系统的设计理.但是对于圆形振子的厚度剪切振动即扭转振动.尚缺乏系统的设计理论.随着科学技术的发展.一些新的超声应用技术.例如,超声电机,超声旋转加工,超声疲劳试验以及超声环焊等得到了压电与声光1994年迅速的发展.在这些技术中需要扭转振动超声换能器,而扭转振动超声换髓器的换能元件多为切向极化的压电陶瓷圆片,其振动模式就是圆片的厚度剪切振动,即扭转振动.因此,为了合理设计扭转振动超声换能器,必须对压电陶瓷圆片振子的厚度剪切振动进行系统的理论研究.另一方面,压电陶瓷圆片振子的厚度剪切振动模式属于压电陶瓷振子众多振动模式的一种,为了保证振子振动模式研究理论的完整性,作为一种补充,也必须研究压电陶瓷圆片振子的厚度剪切振动,即扭转振动.本文从压电陶瓷振子的基本方程,即压电和运动方程出发,对压电陶瓷圆片振子的厚度剪切振动进行了研究,得出了振子扭转角及扭矩的分布规律,推出了振子的机电等效线路及频率方程,提出了截面扭转系数的概念,对于扭转振动换能器的进一步研究及振子振动模式理论的进一步完善,具有一定的指导意义.2切向极化压电陶瓷薄圆片的厚度剪切振动分析夸压电陶瓷薄圆片振子的半径及厚度分别为和,授化方向沿圆周的切向,即口方向,电极涂在振子的上下两主平面上,工作时振子的外加激励电场方向沿着=轴,如图1所示,其中箭头所示方向表示振子的极化方向. OSC表示外加激励源.对于压电陶瓷薄圆片的厚度剪切振动,由于横向尺寸即振子的半径远大于其厚度,而厚度与剪切波波长可相比拟,因此,可以只考虑沿厚度方向的传播波,而把振子的横向看成是陛受夹的,故只有应变分量8≠0,而其它应变分量都等于零.另外,由于假定振子材料是绝缘的,没有漏泄电流,同时忽略边缘效应,因此有一n一0,≠0,等=0,当选择应变及电位移D作为自变量时,可得以下压电方程:=c☆一^l;(1):=一15+ID(2)式中,及为切向应力及应变;及且为电位移及电场强度的轴向分量,以为恒电位移下的弹性刚度常数;s是压电劲度常数;为恒应变下的介电隔离率.令为压电陶瓷剪切振动的扭转角,在薄圆片的条件下,扭转角与切应变的关系为:=r(3)式中,r表示振子中任一点的半径.由于压电陶瓷振子的振动由电路及机械运动两部分决定,因此下面分别进行研究.图1切向极化压电陶瓷薄圆片2.t振予的机械运动方程式振子振动时,其内部任一横截面处的扭矩由下式决定:一Ⅱ?础(4)式中,8表示压电陶瓷圆片振子的横截面积, 把式(1)代入式(4),利用瓯的表达式(3)积分后,可得:一如JP一^sD,W(5)式中,j,一/,2称为振子的截面授惯性矩;一对于振子内部厚为如的任一微分元,其力矩平衡方程为:=.㈣式中,0一r加一Ⅱp出?掰='=为振子内厚为出部分的转动惯量.把式(5)代入式(6),利用aD=/az一0,可得振子的运动方程为:磐:(7)一第2期压电陶瓷薄圜片振子的厚度剪切振动式中m一(c/P)"为压电陶瓷薄圆片中的剪切渡的传播速度,也就是扭转波的传播速度对于简谐振动,令妒一(=)",代入式(7)可得:)一0(8)式中,一q为剪切波波数.由式(8)的解可得压电陶瓷薄圆片振子扭转振动的扭转角分布为:一(Asink,z+Bcosk,z)e~(9)式中,A,B为待定常数,可由振子的边界条件决定,令及忱为振子两端面的扭转角,由此可得以下边界条件:10一1,1一一(10)把式(9)代入式(10)可得待定常数A和口为:A一一丝!e--ja",口一一(11)slnktl把式(11)代入式(9)可得扭转角的分布规律为;一—~p]—si—nk—,(—l--.z_)---—~p—]si—nkjz(12)smag把式(12)代入式(5)可得扭矩的分布函数为:一一~sl,k,9]e~sk'(1--z)'-FePze~sk'z一15DW(13)令Mt和Mz分别为振子两端面的外加力矩,即MI一0一一M1,MI=一M2(I4)把式(13)代入式(14)可得以下运动方程:^f1一cj^—qhco五skd4广-一q~z1_,n.15D;W(15) 2=砖,,-塑±si堕n/.-竺,/!塑+^15D,W(16)2.2压电陶瓷薄圃片振子的电路状态方程式把式(2)两边沿振子的横截面取面积分可得;Els一一h|88+fir,1D8-L17)把8一r譬代入上式积分后可得:B一一耋+鼠(I8)式中,8为振动的横截面积.由式(18)可得振子两端的电压为:—E~dz=--h-s如+(19)因为振子两端面的扭转角分别为和,故j—(2.)把式(20)代入式(I9)可得:一,s(+)+D,l(21)令流过振子的电流为j,它与电荷量口,电位移D;之间的关系为:等一瑚一(22)由式(22)求出D;后代入式(21)可得:一(+)+所,丽1(23)利用式(23)解出电流j可得:l=~oV--n(+如)(24)式中,一却-,一脚z,和为振子两端面的扭转角速度{一为振子厚度剪切振动的截止电容;一!为振子厚度剪切振动模式的机电转换系数.式(24)就是振子的电路状态方程式.2.3振子的机电等效因把式(21)的两边乘以机电转换系数可得:一(,+鼽),+(25)由n的表达式可得:his一硝L(26)把的表达式及式(26)代入式(25)可得:一(+南瓦+.^s(27)由式(27)可得:,..!D,h,s一一(+孟(28)把式(28)代入运动方程式(15)~(16)可得: ,r业+一(+z彘'29)压电与声光=蹦,+一(+)(30)裁羁砖=娼.可得如l=t令z一,称为压电陶瓷薄圆片振子厚度剪切振动或扭转振动的特性声阻抗,可把式(29)~式(30)化为:^f=(一)(+南)+jz_tg等?+(31):=(南一彘)(,+弘ftg?+(32)利用式(24),式(31)~(32)三式可得压电陶瓷圆片振子厚度剪切振动的机电等效图,见图2,其中zt=弘flg譬一z:=丽mr,很显然,图2与压电陶瓷细棒纵向振动的机电等效图,薄一图2压电陶瓷薄圜片振子厚度剪切振动的机电等效图片厚度伸缩以及矩形薄片的厚度剪切振动的机电等效图是类似的.由此可以看出,压电陶瓷薄圆片的厚度剪切振动模式是一种刚度振动模式,即纵效应振动.因为振子激发电场的方向平行于剪切波的传播方向.另外,由剪切波的传播方向垂直于质点的振动方向(切向),故振子中的波动是一种横渡2.4压电陶瓷薄圊片振子厚度剪切振动的频率方程当振子的两端不受外加力矩作用时,即振子自由振动时,外加力矩^f及Ⅳz等于零.此时,由图2可得振子的输入电阻抗z'为:㈣,式中,s磊h;sW为压电陶瓷薄圆片振子厚度剪切振动的机电耦合系数.令一嚣为振子的截面扭转系数,很显然,该系数仅与振子的截面形状及尺寸有关.由,及的定义式,对于实心圆片=詈;对于内外半径分别为n和n.的空心圆片,=兰尝妄,由的定义式可把机电再干r'田刚慰xA口|L电耦合系数Hs化为:=—:(34)庸【谁f由式(33)可得振子的频率方程.当Z.=0时,振子的共振频率方程为:tg1一(5).—;÷=0(35)2当z'一..时,振子的反共振频率方程为:tgk,l=∞(36)由上述分析可以看出,由于振子的厚度剪切振动模式是一种刚度振动模式,因此其传播速度,共振频率方程等都与振子的电学边界条件以及压电常数有关.如果压电陶瓷振子的机电耦合系数码s比较小,即压电效应较弱,作为一种近似,可把振子的共振及反共振频率近似看为相等的.5结论本文研究了切向极化压电陶瓷圆片的厚度剪切振动,所得结果对于扭转振动超声换能器的设计及计算以及压电陶瓷振子振动模式的系统研究具有一定的指导意义,具体结论如下:本文得出了压电陶瓷薄圆片振子的机电等效图及频率方程;b.引入了振子截面扭转系数的概念,该(下转第4】页)第2期氧化锌压电薄膜传感器设计理论研究(上接第36页)系数仅与振子的截面形状及几何尺寸有关} c.压电陶瓷薄圆片振子的厚度剪切振动即扭转振动是一种刚度振动筷式,即纵效应振动,而传播的是一种横波Id.本文理论适用于压电陶瓷薄圆片,即要求振子的半径远大于其厚度.参考文献1张沛霖.张仲渊.压电测量.北京:国防工业出版社.19832栾桂冬.张金铎.王仁乾.压电换能器和换能器阵.北京z北京大学出版社,19903王矜奉.姜祖桐.石瑞大.压电振动,北京科学出版杜.1989。

1.1压电材料概述 1.1.1压电效应1880年法国物理学家皮埃尔和雅各居里兄弟在研究石英晶体的物理性质时 发现:当沿着晶片的某些方向施加作用力使晶片发生变形后, 晶片上相对的两个 表面会出现等量的正负电荷,电荷的密度与施加的力的大小有关, 这种现象称为 压电现象,具有压电现象的介质称为压电体。
压电效应反应了晶体的弹性性能与介电性能之间的耦合。
当对压电陶瓷施加一个与极化方向平行的压力F ,如图1.1( a )所示,陶瓷片将产生压缩变形,片 内的正、负束缚电荷之间的距离变小,极化强度也变小。
因此,原来吸附在电极 上的自由电荷,有一部分被释放,片内的正、负电荷之间的距离变大,极化强度 也变大,因此电极上又吸附一部分自由电荷而出现充电现象。
这种由机械效应转变为电效应的现象就是压电效应。
压电效应包括正压电效应和逆压电效应。
如图 所示: 图1.1压电效应示意图:(a )正压电效应(b )负压电效应正压电效应:当压电晶体在外力作用下发生形变时,在它的某些相对应的面 上产生异号电荷,这种没有电场作用,只是由于形变产生的极化现象称为正压电 效应。
逆压电效应:当压电晶体施加一电场时,不仅产生了极化,同时还产生了形 变,这种由电场产生形变的现象称为逆压电效应。
1.1.2压电陶瓷的诞生与发展具有压电效应性能的陶瓷称为压电陶瓷, 1942年美国麻省理工学院绝缘研究室发现,在钛酸钡铁电陶瓷上施加直流高压电场,使其自发极化沿电 场方向择优取第一章绪论向,除去电场后仍能保持一定的剩余极化,使它具有压电效应,从此诞生了压电陶瓷。
钛酸钡(BaTiO s )陶瓷的发现促进了压电材料的发展,它不但使压电材料从一些单晶体材料发展到压电陶瓷等多晶体材料,而且在压电性能上也有了大幅度提高。
当今广泛应用的压电陶瓷是PZT,即Pb Zr,Ti O3压电陶瓷,其压电效应强,稳定性好。
它是由美国学者B.贾菲等人于1954年发现的PbZrO3 - PbTiO3二元系固溶体压电陶瓷,其机械品质因数约为钛酸钡(BaTiO 3)陶瓷的两倍。