noip2002 提高组 复赛试题及参考程序(pascal)

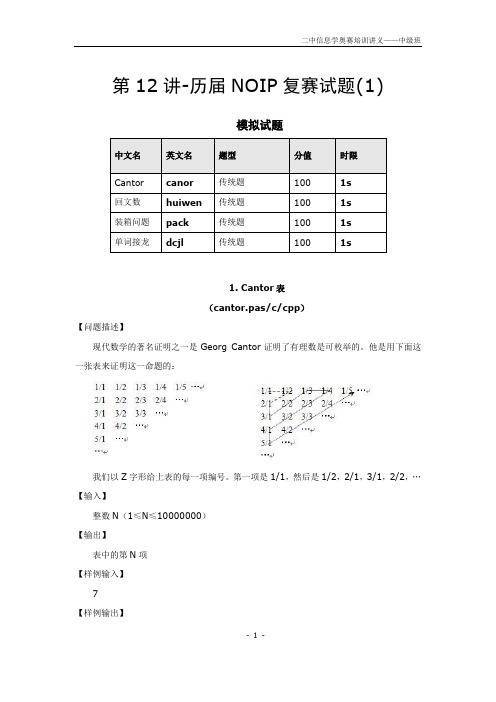
第12讲-历届NOIP复赛试题(1)模拟试题1. Cantor表（cantor.pas/c/cpp）【问题描述】现代数学的著名证明之一是Georg Cantor证明了有理数是可枚举的。

他是用下面这一张表来证明这一命题的：我们以Z字形给上表的每一项编号。

第一项是1/1，然后是1/2，2/1，3/1，2/2，…【输入】整数N（1≤N≤10000000）【输出】表中的第N项【样例输入】7【样例输出】- 1 -1/4【分析】基础题，模拟。

首先确定所在斜行，然后针对奇数行和偶数行进行计算。

【参考代码】varn,x:longint ;beginassign(input,'cantor.in');reset(input);assign(output,'cantor.out');rewrite(output);readln(n);x:=0;repeat//确定所在的斜行inc(x);n:=n-x ;until n<=0;if x mod2=0then write((x+n),'/',(1-n))//确定如何输出else writeln((1-n),'/',(x+n));close(input);close(output );end.2. 回文数（huiwen.pas/c/cpp）【问题描述】若一个数（首位不为零）从左向右读与从右向左读都一样，我们就将其称之为回文数。

例如：给定一个10进制数56，将56加56（即把56从右向左读），得到121是一个回文数。

又如：对于10进制数87：STEP1：87+78 = 165 STEP2：165+561 = 726STEP3：726+627 = 1353 STEP4：1353+3531 = 4884在这里的一步是指进行了一次N进制的加法，上例最少用了4步得到回文数4884。

写一个程序，给定一个N（2<=N<=10，N=16）进制数M，求最少经过几步可以得到回文数。

第十届全国信息学奥林匹克分区联赛（NOIP2004）复赛试题（提高组竞赛用时：3小时）1、津津的储蓄计划(Save.pas／dpr／c／cpp)【问题描述】津津的零花钱一直都是自己管理。

每个月的月初妈妈给津津300元钱，津津会预算这个月的花销，并且总能做到实际花销和预算的相同。

为了让津津学习如何储蓄，妈妈提出，津津可以随时把整百的钱存在她那里，到了年末她会加上20％还给津津。

因此津津制定了一个储蓄计划：每个月的月初，在得到妈妈给的零花钱后，如果她预计到这个月的月末手中还会有多于100元或恰好100元，她就会把整百的钱存在妈妈那里，剩余的钱留在自己手中。

例如11月初津津手中还有83元，妈妈给了津津300元。

津津预计11月的花销是180元，那么她就会在妈妈那里存200元，自己留下183元。

到了11月月末，津津手中会剩下3元钱。

津津发现这个储蓄计划的主要风险是，存在妈妈那里的钱在年末之前不能取出。

有可能在某个月的月初，津津手中的钱加上这个月妈妈给的钱，不够这个月的原定预算。

如果出现这种情况，津津将不得不在这个月省吃俭用，压缩预算。

现在请你根据2004年1月到12月每个月津津的预算，判断会不会出现这种情况。

如果不会，计算到2004年年末，妈妈将津津平常存的钱加上20％还给津津之后，津津手中会有多少钱。

【输入文件】输入文件save.in包括12行数据，每行包含一个小于350的非负整数，分别表示1月到12月津津的预算。

【输出文件】输出文件save.out包括一行，这一行只包含一个整数。

如果储蓄计划实施过程中出现某个月钱不够用的情况，输出-X，X表示出现这种情况的第一个月；否则输出到2004年年末津津手中会有多少钱。

【样例输入1】29023028020030017034050908020060【样例输出1】-7【样例输入2】29023028020030017033050908020060【样例输出2】1580【问题描述】在一个果园里，多多已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。

第八届全国青少年信息学奥林匹克联赛(NOIP2002)试题(普及组PASCAL语言二小时完成)全部试题答案均要求写在答卷纸上,写在试卷纸上一律无效一.选择一个正确答案代码(A/B/C/D,填入每题的括号内(每题1.5分,多选无分,共30分)1)微型计算机的问世是由于( ) 的出现。

A) 中小规模集成电路 B) 晶体管电路 C) (超)大规模集成电路 D) 电子管电路2)下列说法中正确的是( ) 。

A) 计算机体积越大,其功能就越强B) CPU的主频越高,其运行速度越快C) 两个显示器屏幕大小相同,则它们的分辨率必定相同D)点阵打印机的针数越多,则能打印的汉字字体越多3)Windows98中,通过查找命令查找文件时,若输入F*.? , 则下列文件( ) 可以被查到。

A) F.BAS B) FABC.BAS C) F.C D) EF.4)CPU处理数据的基本单位是字,一个字的字长( ) 。

A) 为8个二进制位 B) 为16个二进制位C) 为32个二进制位 D) 与芯片的型号有关5)资源管理器的目录前图标中增加"+"号,这个符号的意思是( ) 。

A) 该目录下的子目录已经展开 B) 该目录下还有子目录未展开C) 该目录下没有子目录 D) 该目录为空目录,6)下列哪一种程序设计语言是解释执行的( ) 。

A) Pascal B) GWBASIC C) C++ D) FORTRAN7)启动WORD的不正确方法是( ) 。

A) 单击Office工具栏上的Word图标B) 单击"开始"→"程序"→WordC) 单击"开始"→"运行",并输入Word按回车D) 双击桌面上的"Word快捷图标"8)多媒体计算机是指( ) 计算机。

A) 专供家庭使用的 B) 装有CDROM的C) 连接在网络上的高级 D) 具有处理文字、图形、声音、影像等信息的9)在树型目录结构中,不允许两个文件名相同主要是指( ) 。

第十二届全国信息学奥林匹克分区联赛（NOIP2006）复赛试题（提高组竞赛用时：3小时）关于竞赛中不同语言使用限制的说明一．关于使用Pascal语言与编译结果的说明1．对于Pascal语言的程序，当使用IDE和fpc编译结果不一致时，以fpc的编译结果为准。

2．允许使用数学库(uses math子句)，以及ansistring。

但不允许使用编译开关（最后测试时pascal的范围检查开关默认关闭：{$R-,Q-,S-}），也不支持与优化相关的选项。

二．关于C++语言中模板使用的限制说明1．允许使用的部分：标准容器中的布尔集合，迭代器，串，流。

相关的头文件：<bitset > <iterator > <string > <iostream >2．禁止使用的部分：序列：vector，list，deque序列适配器：stack, queue, priority_queue 关联容器：map, multimap, set, multiset 拟容器：valarray 散列容器：hash_map, hash_set, hash_multimap, hash_multiset 所有的标准库算法相关头文件：<vector > <list > <deque > <stack > <map > <set > <algorithm >1．能量项链(energy.pas/c/cpp)【问题描述】在Mars星球上，每个Mars人都随身佩带着一串能量项链。

在项链上有N颗能量珠。

能量珠是一颗有头标记与尾标记的珠子，这些标记对应着某个正整数。

并且，对于相邻的两颗珠子，前一颗珠子的尾标记一定等于后一颗珠子的头标记。

因为只有这样，通过吸盘（吸盘是Mars人吸收能量的一种器官）的作用，这两颗珠子才能聚合成一颗珠子，同时释放出可以被吸盘吸收的能量。

NOI’ 95“同创杯”全国青少年信息学（计算机）奥林匹克竞赛分区联赛复赛试题（高中组）（上机编程，完成时间：210 分钟）<1>编码问题：设有一个数组A:ARRAY[0..N-1] OF INTEGER；数组中存放的元素为0～N-1 之间的整数，且A[i]≠ A[j]（当i≠ j时）。

例如： N=6 时，有：此时，数组 A 的编码定义如下：A[0] 的编码为0；A[i] 的编码为：在A[0] ，A[1]∴上面数组 A 的编码为：A= （ 4，3， 0， 5，1， 2），， A[i-1] 中比 A[i] 的值小的个数（B= （0， 0，0，3，1， 2）i=1 ，2，， N-1 ）程序要求解决以下问题：①给出数组 A 后，求出其编码。

②给出数组 A 的编码后，求出 A 中的原数据。

<2> 灯的排列问题：设在一排上有 N 个格子（ N≤ 20），若在格子中放置有不同颜色的灯，每种灯的个数记为 N 1， N2， N k（ k 表示不同颜色灯的个数）。

放灯时要遵守下列规则：①同一种颜色的灯不能分开；②不同颜色的灯之间至少要有一个空位置。

例如： N=8 （格子数）R=2 （红灯数）B=3 （蓝灯数）放置的方法有：R-B 顺序R R B B BR R B B BR R B B BR R B B BR R B B BR R B B BB-R顺序B B B BBBBBBBBBBBBBBR RRRBRRRRRRRR放置的总数为12 种。

数据输入的方式为：NP1（颜色，为一个字母）P2N1（灯的数量）N2Q（结束标记， Q 本身不是灯的颜色）程序要求：求出一种顺序的排列方案及排列总数。

<3> 设有一个四层的积木块，1～ 4 层积木块的数量依次为：5， 6，7， 8如下图所示放置：815851691423414326其中，给出第三层与第四层所标示的数字，并已知第三层的数据是由第四层的数据计算出来的。

NOIP2002复习资料作者：徐沛来2002．11．23NOIP2002复习资料作者徐沛来第一章 Pascal函数与技巧一、常用函数与过程：* abs(x):y取x的绝对值，x与y可为整型或实型。

* append(f:text)用赋给f的文件名打开存在的外部文件。

如果不存在给定的文件，产生错误。

如果f已经存在，就先关闭再重新打开它。

当前文件指针指向文件尾。

* frac(x):y取x的小数部分，x与y均为实型。

* int(x):y取x的整数部分，x与y均为实型，常写成trunc(int(x)).* random(x):y在0-x之间的整数中随机找一个整数，x与y均为整型。

* sin(x):y; cos(x):y; arctan(x):y; exp(x):y; ln(x):y均与数学运算一致,三角函数返回的均为弧度,转换成角度即乘以Pi除以180.* copy(str,n1,n2):substr从字符串str中取从第n1个字符开始长度为n2个字符的子串substr.n1和n2是整型表达式，如果n1大于s的长度，则返回空字符串。

如果指定的n2大于第n1个字符后剩下的字符数，则返回剩下的字符串。

* pos(substr,str):num查找substr是否为str的子串，若是则返回substr在str中的起始位置，若否则返回0.* val(str,int,code)将字串str转为数值型数据存入int, 如果字符串无效，其中非法字符的下标放在Code 中；否则，code为零。

* str(num,str)将num表达式转成字符串str。

* delete( str,n1,n2)从原字符串str中删去一个从n1开始长度为n2的子串，如果Index比s长，不删除任何字符。

如果指定的Count大于从第1ndex大到结尾的字符数，删除剩余部分。

NOIP2002复习资料 作者 徐沛来* Insert(Source ：String ；Var S ：String ；Index ：Integer)Source 是字符串表达式。

第八届全国青少年信息学奥林匹克联赛（NOIP2002）初赛试题（提高组PASCAL语言二小时完成）审定：全国青少年信息学奥林匹克竞赛科学委员会主管：中国科协、教育部主办：中国计算机学会承办：江苏省科协青少年科技中心●●全部试题答案均要求写在答卷纸上，写在试卷纸上一律无效●●一．选择一个正确答案代码（A/B/C/D），填入每题的括号内（每题1.5分，多选无分，共30分）1．微型计算机的问世是由于（）的出现。

A）中小规模集成电路B）晶体管电路C）（超）大规模集成电路D）电子管电路2．中央处理器（CPU）能访问的最大存储器容量取决于（）。

A）地址总线B）数据总线C）控制总线D）实际内存容量3．十进制书11/128可用二进制数码序列表示为：（）。

A）1011/1000000 B）1011/100000000 C）0.001011 D）0.00010114．算式（2047）10 －（3FF）16 ＋（2000）8的结果是（）。

A）（2048）10B）（2049）10C）（3746）8D）（1AF7）165．已知x =（0.1011010）2，则[ x / 2 ]补=（）2 。

A）0.1011101 B）11110110 C）0.0101101 D）0.1001106．IPv4地址是由（）位二进制数码表示的。

A）16 B）32 C）24 D）87．计算机病毒传染的必要条件是：（）。

A）在内存中运行病毒程序B）对磁盘进行读写操作C）在内存中运行含有病毒的可执行的程序D）复制文件8．在磁盘上建立子目录有许多优点，下列描述中不属于建立子目录优点的是（）。

A）便于文件管理B）解决根目录中目录项个数有限问题C）加快文件查找速度D）节省磁盘使用空间9．在使用E-mail前，需要对Outlook进行设置，其中ISP接收电子邮件的服务器称为（）服务器。

A）POP3 B）SMTP C）DNS D）FTP10．多媒体计算机是指（）计算机。

Day1铺地毯【问题描述】为了准备一个独特的颁奖典礼，组织者在会场的一片矩形区域（可看做是平面直角坐标系的第一象限）铺上一些矩形地毯。

一共有n 张地毯，编号从1 到n。

现在将这些地毯按照编号从小到大的顺序平行于坐标轴先后铺设，后铺的地毯覆盖在前面已经铺好的地毯之上。

地毯铺设完成后，组织者想知道覆盖地面某个点的最上面的那张地毯的编号。

注意：在矩形地毯边界和四个顶点上的点也算被地毯覆盖。

【输入】输入文件名为 carpet.in。

输入共 n+2 行。

第一行，一个整数 n，表示总共有n 张地毯。

接下来的 n 行中，第i+1 行表示编号i 的地毯的信息，包含四个正整数a，b，g，k，每两个整数之间用一个空格隔开，分别表示铺设地毯的左下角的坐标（a，b）以及地毯在x轴和y 轴方向的长度。

第 n+2 行包含两个正整数x 和y，表示所求的地面的点的坐标（x，y）。

【输出】输出文件名为 carpet.out。

输出共 1 行，一个整数，表示所求的地毯的编号；若此处没有被地毯覆盖则输出-1。

【输入输出样例 1】【输入输出样例说明】如下图，1 号地毯用实线表示，2 号地毯用虚线表示，3 号用双实线表示，覆盖点（2，2）的最上面一张地毯是3 号地毯。

【输入输出样例 2】【输入输出样例说明】如上图，1 号地毯用实线表示，2 号地毯用虚线表示，3 号用双实线表示，点（4，5）没有被地毯覆盖，所以输出-1。

【数据范围】对于 30%的数据，有n≤2；对于 50%的数据，0≤a, b, g, k≤100；对于 100%的数据，有0≤n≤10,000，0≤a, b, g, k≤100,000。

【一句话题意】给定n个按顺序覆盖的矩形，求某个点最上方的矩形编号。

【考察知识点】枚举【思路】好吧我承认看到图片的一瞬间想到过二维树状数组和二维线段树。

置答案ans=-1，按顺序枚举所有矩形，如果点在矩形内则更新ans。

注意题中给出的不是对角坐标，实际上是(a,b)与(a+g,b+k)。

全国信息学奥林匹克分区联赛（NOIP）复赛提高组试题第一届全国信息学奥林匹克分区联赛（NOIP1995）复赛试题（提高组竞赛用时：3.5小时）1、编码问题设有一个数组A:ARRAY[0..N-1]OFINTEGER；数组中存放的元素为0～N-1之间的整数，且A[i]≠A[j]（当i≠j时）。

例如：N=6时，有：A=（4，3，0，5，1，2）此时，数组A的编码定义如下：A[0]的编码为0；A[i]的编码为：在A[0]，A[1]，…，A[i-1]中比A[i]的值小的个数（i=1，2，…，N-1）∴上面数组A的编码为：B=（0，0，0，3，1，2）程序要求解决以下问题：①给出数组A后，求出其编码。

②给出数组A的编码后，求出A中的原数据。

2、灯的排列问题设在一排上有N个格子（N≤20），若在格子中放置有不同颜色的灯，每种灯的个数记为N1，N2，……N k（k表示不同颜色灯的个数）。

放灯时要遵守下列规则：①同一种颜色的灯不能分开；②不同颜色的灯之间至少要有一个空位置。

例如：N=8（格子数）；R=2（红灯数）；B=3（蓝灯数），放置的方法有：R-B顺序B-R顺序放置的方法总数为12种。

数据输入的方式为：NP1（颜色，为一个字母）N1（灯的数量）P2 N2……Q（结束标记，Q本身不是灯的颜色）程序要求：求出一种顺序的放置（排列）方案及放置（排列）方案总数。

3、积木块上的数字设有一个四层的积木块，1～4层积木块的数量依次为：5，6，7，8，如下图所示放置：其中，给出第三层与第四层所标示的数字，并已知第三层的数据是由第四层的数据计算出来的。

计算的方法是：第三层的某个数据A是由第四层相邻的两个数据B，C经过某种计算后产生的：计算所用到的计算符为：+，-，⨯，且无优先级之分（自左向右计算），运算符最多为2个。

如：3+4⨯5=35 5⨯4+3=23可以看出，上图中的第三层的数据是由第四层的数据用以下计算公式计算出来的：A=B⨯C+B也就是：8=2⨯3+2，15=3⨯4+3，……14=2⨯6+2程序要求：给出第四层与第三层的数据后，将第一、二层的每块积木标上相应的数据，并输出整个完整的积木图及计算公式。

NOIP 提高组初赛历年试题及答案阅读题篇程序写果（共 4 ，每 8 分，共 32 分）程序的最好方法并非是依次从到尾。

程序不像迷，我无法从末尾几找到答案，也不像一本引人入的籍，只需直接翻到褶最多的那几，我就能找到最精彩的片断。

因此我在程序，最好逐一考察研究每一段代，搞清楚每一段代的来去脉，理解每一段代在程序中所起的作用，而形成一个虚的程序构，并以此基来行。

1、分：高入手，逐深入，正确理解程序。

2、写注解：固化、、提已有的理解成果。

3、先模：根据代序跟踪量，模运算。

4、找律：先模几次循后，找出背后的律。

5、看功能：从代构和运算果判断程序功能。

6、猜算法：有不知道算法，通构和函数猜一猜。

7、方法：了解程序本后，一个熟悉的方法。

大多数人来，写程序是令人开心的一件事情，人的程序却很痛苦，很恐惧，宁愿自己重写一遍。

其到好的程序，就像一篇美文，令人心神怡，豁然开朗，因背后是一个人的思，甚至整个人生。

人的程序不可以巩固自己的知，启自己的思，提升自己的修养，你收，其，也是在学、在、在工作中的最重要、最常用的基本功。

如果写程序是把自己的思化代，程序就是把代化你理解的人的思。

当你程序有烈的代入感，像演一，真正入到的精神世界，面部表情也随之日丰富起来。

祝你！你通关了！之，看得多，得多，拼得多，你就考得多⋯⋯NOIP2011-1 ．#include <iostream>#include <cstring>using namespace std;const int SIZE = 100;int main(){int n,i,sum,x,a[SIZE];cin>>n;memset(a,0,sizeof(a));for(i=1;i<=n;i++){cin>>x;a[x]++;}i=0;sum=0;while(sum<(n/2+1)){i++;sum+=a[i];}cout<<i<<endl;return 0;}输入：114 5 6 6 4 3 3 2 3 2 1一步步模拟，注意输出的是sum超出循环条件时的i 值（中位数），而不是sum ，也不是a[x]输出： 3NOIP2011-2 ．#include <iostream> using namespace std; int n;void f2(int x,int y); void f1(int x,int y){if(x<n)f2(y,x+y);}void f2(int x,int y){cout<<x<<' ';f1(y,x+y);}int main(){cin>>n;f1(0,1);return 0;}输入： 30此为简单的递归题，依次输出f2(x,y)中的x值，注意边界条件时f1(x,y)的x>=30咦！这不是隔一个输出一个的Fibonacci吗？输出： 1 2 5 13 34NOIP2011-3 ．#include <iostream>using namespace std; const int V=100;int n,m,ans,e[V][V];bool visited[V];void dfs(int x,intlen){int i;visited[x]= true;if(len>ans)ans=len;for(i=1;i<=n;i++)if( (!visited[i]) &&(e[x][i]!=-1) ) dfs(i,len+e[x][i]);visited[x]=false;}int main(){int i,j,a,b,c;cin>>n>>m;for(i=1;i<=n;i++)for(j=1;j<=m;j++)e[i][j]=-1;for(i=1;i<=m;i++){cin>>a>>b>>c;e[a][b]=c;e[b][a]=c;}for(i=1;i<=n;i++)visited[i]=false;ans=0;for(i=1;i<=n;i++)dfs(i,0);cout<<ans<<endl;return 0;}输入：4 61 2 102 3 203 4 304 1 401 3 502 4 60一看就知这是深搜算法（DFS ），输入是个四个顶点的无向图（邻接矩阵如下）：如len>ans，则 ans=len，可以说明这是个在图中用DFS找最长的路径的程序。