圆 系
关 置
与 圆
的 位
2008 新北京新奥运
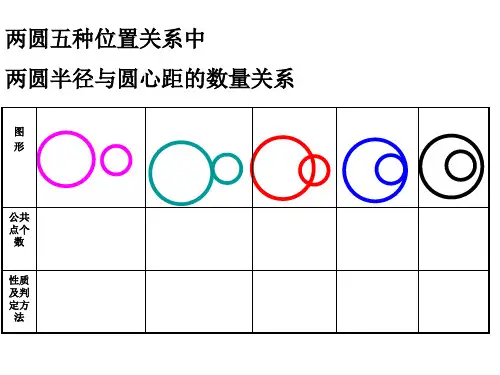
认真观察 观察结果
外离:两圆无公共点,并且每个圆上的点都在另 一个圆的外部时,叫两圆外离
切点
外切:两圆有一个公共点,并且除了公共点外, 每个圆上的点都在另一个圆的外部时,叫两 圆外切
相交:两圆有两个公共点时,叫两圆相交 切点
内切:两圆有一个公共点,并且除了公共点外,一个 圆上的点都在另一个圆的内部时,叫两圆内切
已知:⊙O1和⊙O2的半径分别2cm和4cm,当圆心 距O1O2分别为下列数值时,判断两圆位置关系.
(1)0cm (2)8 cm
特例
内含:两圆无公共点,并且一个圆上的点都在另一 个圆的内部时,叫两圆内含
圆心距:两圆心之间的距离
外离
外切
相交
内切
内含同心圆
圆
外离
与
相离
圆 的
内含
位
外切
置
相切
关
系
内切
相交
两圆位置关系的性质与判定:
演示
0
两圆外离
位置关系
R―r
性质
d 和R、 r关系
Rr
d >R+ r
两圆外切
d =R+ r
两圆相交
判断: 1 两圆无公共点,两圆一定外离 ( )
已知:⊙O1和⊙O2的半径分别2cm和4cm,当圆心距O1O2 分别为下列数值时,判断两圆位置关系.
(1)2cm (2)4 cm 3 6 cm
判断: 2 当两圆圆心距大于半径之差 时,两圆相交( )
判断: 3 已知两圆相切R=7, r=2则圆心距等于9 ( )
同 心 圆 两圆内切 内
含;R+ r