- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
BC=4cm,以C为圆心,r为半径的圆与AB 有怎样的位置关系?为什么? (1)r=2cm;(2)r=2.4cm (3)r=3cm.
B
4
D
d
C
A
3
.
解:过C作CD⊥AB,垂足为D
在△ABC中,
AB= AC2 BC2 32 42 5
根据三角形的面积公式有
1CD AB1ACBC
2
2
∴ C D A C B C 342.4(c)m
B
(1) r=2cm
D
(2) r=4cm
(3) r=2.5cm
A
●
M
C
.
B
3、如图,在Rt△ABC中,∠C=90°,AB=5cC m,
AC=3cm,以C为圆心的圆与AB
相切,则这个圆的半径是
12cm。 5
A
4、直线L 和⊙O有公共点,则直线L与⊙O( D ). A、相离;B、相切;C、相交;D、相切或相交。
dr
直线和圆相交
d< r
∟ ∟
r d
r d
直线和圆相切
d= r
直线和圆相离 位置关系
.
d> r
数量关系
总结: 判定直线 与圆的位置关系的方法有两____种:
(1)根据定义,由___直___线___与___圆__的__ 公共点 的个数来判断;
(2)根据性质,由__圆__心__到___直__线__的__距__离d与半径r 的关系来判断。
在实际应用中,常采用第二种方法判定。
.
小试牛刀
1、已知圆的直径为13cm,设直线和圆心的距离为d : 1)若d=4.5cm ,则直线与圆 相交 , 直线与圆有__2__个公共点. 2)若d=6.5cm ,则直线与圆_相__切___, 直线与圆有___1_个公共点. 3)若d= 8 cm ,则直线与圆_相__离___, 直线与圆有__0__个公共点.
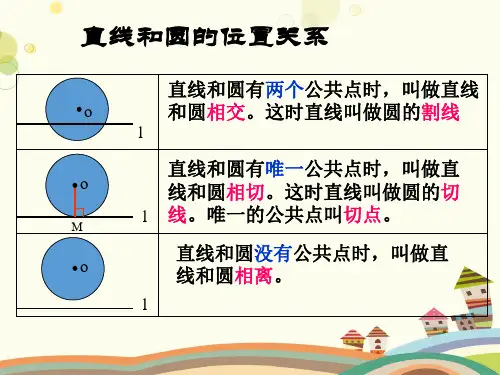
(3)直线和圆没有公共点时, 叫做直线和圆相离。
.
O
l
相交
O
A
l
相切
O
l
相离
上述变化过程中,除了公共点的个数发生了变化, 还有什么量在改变?你能否用数量关系来判别直线 与圆的位置关系?
.
相关知识点回忆
直线外一点到这条直线 的垂线段的长度叫点到直线 的距离。
.A
D
a
.
二、直线和圆的位置关系
(用圆心o到直线l的距离d与圆的半径r的关系来区分)
B
∵CD是⊙O的切线,A是切点,OA是⊙O的半径,
∴CD⊥OA. ●O
C 温馨提示:切线的性质是证明两线垂直的重要根据;
A
D
作过切点的半径是常用的辅助线之一.
.
例1: 在 Rt△ABC中,∠C=90°,斜边AB=8cm,AC=4cm. (1)以C为圆心作圆,当半径为多长时,
AB与⊙C相切? (2)以点C为圆心,分别以2cm和4cm的长为半
.
(2)以点C为圆心,分别以2cm,4cm为半径作两 个圆,这两个圆与AB分别有怎样的位置关系?
解:(2)由(1)可知,圆心到AB的距离 d= 2 3 cm,所以
当r=2cm时,d>r,AB与⊙C相离;
当r=4cm时,d<r,AB与⊙C相交.
.
例2:在Rt△ABC中,∠C=90°,AC=3cm,
2、已知⊙O的半径为5cm, 圆心O与直线AB的距离为d, 根据 条件填写d的范围:
1)若AB和⊙O相离, 则 d > 5cm
;
2)若AB和⊙O相切, 则 d = 5cm ; 3)若AB和⊙O相交,则 0cm≤ d < 5cm.
.
●O 相交
●O 相切
●O 相离
• 上面的三个图形是轴对称图形吗?如果是,你能 画出它们的对称轴吗?
直线和圆的位置关系
.
A C
点和圆的位置关系有几种?
点到圆心的距离为d, B 圆的半径为r,则:
点在圆外 点在圆上 点在圆内
位置关系
.
d>r; d=r; d<r.
数量关系
同学们,在我们的生活中到处都 蕴含着数学知识,下面老师请同 学们欣赏美丽的
海上日出
从海上日出这种自然现象中可以抽象出哪 些基本的几何图形呢?
径作两个圆,这两个圆与AB分别有怎样的 位 置关系?
A
4cm
D 8 cm
C
B
.
解:(1)过点C作CD⊥AB于D.
∵AB=8cm,AC=4cm.
cosA AC1. AB 2
∴∠A=60°.
A D
┐
C
B
C A D sC A i n 4 s6 i0 n 0 2 3 c.m
因此,当半径长为 2 3 cm时,AB与⊙C相切.
AB 5
D
d
即圆心C到AB的距离d=2.4cm
所以 (1)当r=2cm时, 有d>r, 因此⊙C和AB相离。
.
(2)当r=2.4cm时,有d=r, 因此⊙C和AB相切。
D
d
(3)当r=3cm时,有d<r, 因此,⊙C和AB相交。
.
D
d
自我检验
1、已知:圆的直径为13cm,如果直线和圆心 的距离为以下值时,直线和圆有几个公共点? 为什么?
.
拓展 已知⊙A的直径为6,点A的坐标为 (-3,-4),则x轴与⊙A的位置关系是 _相__离__, y轴与⊙A的位置关系是_相__切__。
(1) 4.5cm A、0 个;
答案:C B、1个; C、2个;
(2) 6.5cm A、0 个;
(3) 8cm
答案:B B、1个; C、2个; 答案:A
A、0 个; B、1个; C、2个;
.
2、如图,已知∠BAC=30度,M为AC 上一点,且AM=5cm,以M为圆心、 r为半径的圆与直线AB有怎样的 位置关系?为什么?
.
.
请同学们利用手中的工具再现海上 日出的整个情景。
在再现过程中,你认为直线与圆的 位置关系可以分为哪几类?
你分类的依据是什么?
.
一、直线与圆的位置关系
(用公共点的个数来区分) (1)直线和圆有两个公共点, 叫做直线和圆相交, 这条直线叫圆的割线, 这两个公共点叫交点。
(2)直线和圆有唯一个公共点, 叫做直线和圆相切, 这条直线叫圆的切线, 这个公共点叫切点。
•直径AB与直线CD要么垂直,要么不垂直.
假设AB与CD不垂直,过点O作一条直径垂直于CD,垂足为M,
B
则OM<OA,即圆心到直线CD的距离小于
⊙O的半径,因此,CD与⊙O相交.这与已
知条件“直线与⊙O相切”相矛盾.
●O
所以CD与AB垂直.
C
AM D
.
切线的性质
圆的切线垂直于过切点的直径.
如图
线CD与⊙O相切于点A,直径AB与直线CD有怎样 的位置关系?说说你的理由.
• 直径AB垂直于直线CD.
B
小颖的理由是:
∵右图是轴对称图形,AB是对称轴,
∴沿直线AB对折图形时,AC与AD重合,因
●O
此,∠BAC=∠BAD=90°
C
A
D
.
探索切线的性质
• 小亮的理由是: