第12讲:完美贝叶斯均衡
- 格式:pptx
- 大小:361.24 KB
- 文档页数:97



纯策略贝叶斯纳什均衡例题引言:纯策略贝叶斯纳什均衡是博弈论中常用的概念之一,它可以用于分析多方参与的决策问题。
本文将通过一个例题来解释纯策略贝叶斯纳什均衡的概念及应用。
例题背景:假设有两家咖啡店,分别是A店和B店。
每天早晨,两家咖啡店都需要决定自己的咖啡价格。
同时,消费者也需要决定去哪家咖啡店购买。
假设消费者根据市场情况作出购买决策。
A店和B店的利润与消费者选择有关。
情景一:A店设置较高的价格,B店设置较低的价格。
这种情况下,消费者更愿意选择购买B店的咖啡。
B店的利润将最大化,而A店的利润将最小化。
情景二:A店和B店都设置较低的价格。
这种情况下,消费者会更加倾向于选择购买A店的咖啡。
A店的利润将最大化,而B店的利润将最小化。
情景三:A店和B店都设置较高的价格。
这种情况下,消费者没有购买的动力,两家咖啡店的利润都会很低。
分析与求解:我们可以将上述情景转化为一个博弈论的模型,其中A店和B店是两个决策者,他们需要根据对方的策略来决定自己的策略。
消费者的选择将影响两家咖啡店的利润。
根据纯策略贝叶斯纳什均衡的概念,我们需要确定每个决策者的策略组合,以获得最优的结果。
在这个例题中,我们需要确定A店和B店的咖啡价格。
假设A店有80%的机会成为消费者的首选,B店有20%的机会。
根据这个信息,我们可以得到以下策略组合:情景一:A店设置高价格,B店设置低价格。
情景二:A店设置低价格,B店设置低价格。
情景三:A店设置高价格,B店设置高价格。
然后我们可以计算每种策略组合下两家咖啡店的利润,并找出使两家咖啡店利润最大化的策略组合。
结论:通过计算,我们可以得到以下结果:情景一:A店设置高价格,B店设置低价格。
这种情况下,A店的利润最大化,B店的利润最小化。
因此,纯策略贝叶斯纳什均衡的结果是,A店设置高价格,B店设置低价格时,两家咖啡店的利润最优化。
扩展思考:本例题中我们假设了A店有80%的机会成为消费者的首选,B店有20%的机会。


博弈论——策略互动的艺术_哈尔滨工业大学中国大学mooc课后章节答案期末考试题库2023年1.观察如下的一个博弈树,【图片】下面结论正确的是()。
答案:该博弈实质上是一个二人同时进行的博弈,其中参与人1的策略集为{a,b},参与人2的策略集为{c, d}2.关于纳什均衡、子博弈完美均衡、完美贝叶斯均衡三个概念,下面说法正确的是()。
答案:完美贝叶斯均衡一定是子博弈完美均衡3.关于博弈论纳什均衡的论述,下列说法中,()是正确的。
答案:纳什均衡中任意一个参与人的对应策略,一定是关于该均衡中其他参与人在均衡中的策略或策略组合的最佳应对(best reply)4.下面例子,()不属于博弈行为。
答案:樵夫在森林砍柴,樵夫和树木的关系5.再考虑孩子教育博弈问题,假设博弈支付矩阵如下所示孩子认真学习沉迷游戏母亲溺爱e, 21, f冷酷的爱a, bc, d如果在博弈均衡情况下,孩子的均衡策略是“认真学习”和“沉迷游戏”策略的完全非退化随机化(孩子均以严格正概率选择这两个策略),且博弈只存在一个纳什均衡,那么下面表述为真的选项是( )答案:母亲也必须对“溺爱”和“冷酷的爱”进行完全非退化的随机化(以严格正概率选择“溺爱”和“冷酷的爱”)6.考虑如下的孩子教育博弈,支付矩阵如下(a,b,c均大于0)孩子认真学习沉迷游戏母亲溺爱3, 21, 3冷酷的爱a, bc, d如果希望博弈均衡为(冷酷的爱,认真学习),那么a~d需要满足的条件为()答案:a≥3且b≥d7.对于如下图所示的博弈【图片】若参与人1选择行动L、M和R的概率分别为0.2,0.3和0.5,那么根据“策略-信念”的一致性要求,当博弈到达参与人2的信息集时,下面选项正确的是()。
答案:参与人2认为她在左边决策节点的概率和右边节点的概率分别为0.4和0.6 8.目前新能源汽车在世界范围内处于方兴未艾的状态,关于新能源汽车行业,从博弈“竞合”角度,下面说法合理的是()(可多选)答案:提升电动汽车电池续航能力会增加汽车的价值_适度的国内竞争,会有利于我国新能源汽车行业的发展_在相对偏僻的商场增设充电桩,会实现商场和新能源汽车销售企业的共赢9.关于博弈“竞合”的表述,最为贴切的表述是()答案:竞合的含义是,竞争与合作同时存在的过程10.下面选项哪个不属于破解囚徒困境的方法()答案:事先制定君子协定11.改变博弈的PARTS法中,S的含义是()答案:Scope 博弈的范围12.下面关于博弈树的说法,正确的是()。


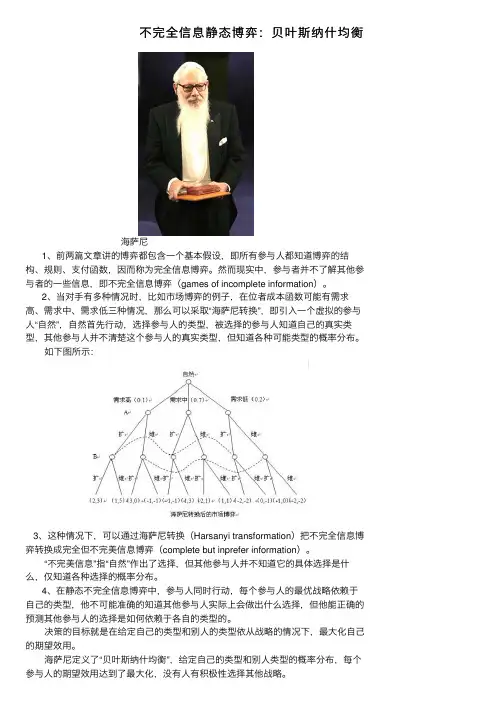
不完全信息静态博弈:贝叶斯纳什均衡海萨尼1、前两篇⽂章讲的博弈都包含⼀个基本假设,即所有参与⼈都知道博弈的结构、规则、⽀付函数,因⽽称为完全信息博弈。
然⽽现实中,参与者并不了解其他参与者的⼀些信息,即不完全信息博弈(games of incomplete information)。
2、当对⼿有多种情况时,⽐如市场博弈的例⼦,在位者成本函数可能有需求⾼、需求中、需求低三种情况,那么可以采取“海萨尼转换”,即引⼊⼀个虚拟的参与⼈“⾃然”,⾃然⾸先⾏动,选择参与⼈的类型,被选择的参与⼈知道⾃⼰的真实类型,其他参与⼈并不清楚这个参与⼈的真实类型,但知道各种可能类型的概率分布。
如下图所⽰:3、这种情况下,可以通过海萨尼转换(Harsanyi transformation)把不完全信息博弈转换成完全但不完美信息博弈(complete but inprefer information)。
“不完美信息”指“⾃然”作出了选择,但其他参与⼈并不知道它的具体选择是什么,仅知道各种选择的概率分布。
4、在静态不完全信息博弈中,参与⼈同时⾏动,每个参与⼈的最优战略依赖于⾃⼰的类型,他不可能准确的知道其他参与⼈实际上会做出什么选择,但他能正确的预测其他参与⼈的选择是如何依赖于各⾃的类型的。
决策的⽬标就是在给定⾃⼰的类型和别⼈的类型依从战略的情况下,最⼤化⾃⼰的期望效⽤。
海萨尼定义了“贝叶斯纳什均衡”,给定⾃⼰的类型和别⼈类型的概率分布,每个参与⼈的期望效⽤达到了最⼤化,没有⼈有积极性选择其他战略。
5、举个例⼦,某⼀市场原来被A企业所垄断,现在B企业考虑是否进⼊。
B企业知道,A企业是否允许它进⼊,取决于A企业阻挠B企业进⼊所花费的成本。
如果阻挠的成本⾼,A企业的最优战略是默许B进⼊。
如果阻挠的成本低,A企业的最优战略是阻挠。
⽀付矩阵如下表所⽰:B企业并不知道A企业的阻挠成本是⾼还是低。
这⾥,某⼀参与⼈本⼈知道、其他参与⼈不知道的信息称为私⼈信息。

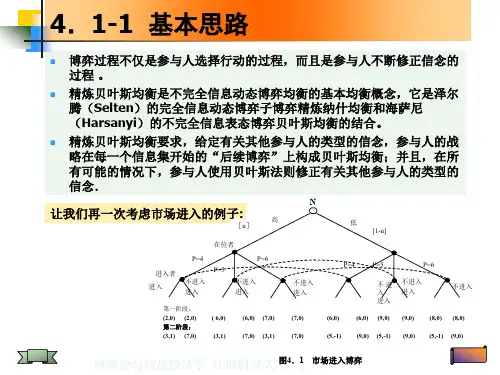
第十二章贝叶斯纳什均衡及其精炼前两章讨论的是完全信息条件下的博弈,给出了博弈的基本分析框架。
本章将讨论不完全信息下的博弈行为,包括不完全信息静态博弈和不完全信息动态博弈。
12.1不完全信息博弈与贝叶斯纳什均衡一、不完全信息博弈完全信息博弈指博弈中的参与人对所有其他参与人的支付(偏好)函数有完全的了解,并且支付函数是所有参与人的共同知识(common knowledge)的博弈。
反之,不满足完全信息博弈假设的博弈称为不完全信息博弈。
二、海萨尼(Harsanyi)转换在博弈中,信息不完全使得博弈参与人必须预测其他参与人的类型。
至于“类型”概念,以两个企业博弈的例子说明。
假设参与人1为在位者企业,参与人2为进入者企业。
进入者依据在位者的生产成本高低选择是否进入该行业,高则进,低则不进。
但是进入者不知道在位者的成本是高还是低。
因此,进入者必须预测在位者的成本“类型”,究竟是高成本的还是低成本的。
海萨尼提出通过引入“自然”概念解决这个问题。
即由自然实现行动,确定其他参与人的类型,从而转换成我们已讨论过的扩展式动态博弈结构。
即通过自然选择类型,实现不完全信息向完全信息的转换,我们称之为海萨尼转换。
在本例中,通过自然选择在位者的成本类型,进入者再针对高成本或低成本进行是否进入的博弈决策。
应当指出,通过自然选择类型的划分,不仅是针对支付函数而言的,其包括参与人所拥有的所有个人信息,如战略空间和信息集等等。
通过上述分析可知道,不完全信息意味着,至少有一个参与人拥有多种类型,否则就成为完全信息博弈。
用表示参与人的一个特定类型,表示参i θi i Θ与人所有可能类型的集合,,并假定i i i Θ∈θ取自某个客观的分布函数。
n i i 1}{=θ),,(1n P θθL为简化起见,假定只有参与人本人观察到自i 己的类型,其他人都不能察到。
但依据海萨尼i θi θ公理,我们假定分布函数是所有参与),,(1n P θθL 人的共同知识,就是说,在博弈开始时,所有参与人关于自然行动的信念是相同的。

论述完美贝叶斯均衡的
定义
完美贝叶斯均衡是一种多人博弈模型,其中所有参与者都独立地做出
最佳决定,以获得最大的利益。
在这种博弈模型中,每个参与者都分
析了他们的行为生成的期望价值,对其进行优化,以获得最大的利润。
该概念可以抽象表示为:一种状况下,当一个人采取了一个行为,其
他人改变自己行为以使自己的利益最大化,并最终达到一种合作平衡。
完美贝叶斯均衡提出的假设是,如果一个参与者的行为可以影响到其
它参与者的利润,那么对他们来说,当他们考虑总利润(以及对其他
参与者的影响)时,他们会选择一种有利于其本身利润和有益于其他
参与者的行为。
因此,这种博弈模型最终可以使所有参与者获得最大
利益。
完美贝叶斯均衡名词解释
嘿,你知道啥是完美贝叶斯均衡不?这可不是个简单的概念啊!咱就说,它就像是一场精彩刺激的游戏里的致胜策略。
比如说,你和朋友玩猜硬币正反面的游戏。
你得根据各种信息去判断朋友会出正面还是反面,这就是在寻找一种平衡。
完美贝叶斯均衡就是在这种复杂的情况下,大家都能做出最明智的选择。
想象一下,在一个商业竞争的场景里,各个公司就像在棋盘上的棋子。
它们要根据对手的行动、市场的变化等等因素来决定自己的下一步。
这时候,完美贝叶斯均衡就是那个能让它们在竞争中站稳脚跟的法宝。
它可不是随随便便就能达到的哦!这需要对各种信息的精准把握和分析。
就好像你要去一个陌生的地方,你得知道路线、天气、当地的风俗习惯等等,才能顺利到达目的地。
再比如,谈恋爱的时候,你和对方的互动也是一种微妙的平衡。
你要根据对方的反应、情绪来调整自己的行为,这也是一种类似完美贝叶斯均衡的状态呀!
完美贝叶斯均衡真的很神奇,它在很多领域都有着重要的作用。
不管是经济、政治,还是我们的日常生活,都能看到它的影子。
它就像是一个隐藏的规则,默默地影响着一切。
总之,完美贝叶斯均衡可不是一般的概念,它是复杂系统中的智慧结晶。
你现在是不是对它有了更深刻的理解呢?我觉得啊,了解它真的能让我们在面对各种情况时更加从容和明智!。
贝叶斯准则法
贝叶斯的统计学中有一个基本的工具叫贝叶斯法则、也称为贝叶斯公式,尽管它是一个数学公式,但其原理毋需数字也可明了。
如果你看到一个人总是做一些好事,则那个人多半会是一个好人。
这就是说,当你不能准确知悉一个事物的本质时,你可以依靠与事物特定本质相关的事件出现的多少去判断其本质属性的概率。
用数学语言表达就是:支持某项属性的事件发生得愈多,则该属性成立的可能性就愈大。
贝叶斯法则又被称为贝叶斯定理、贝叶斯规则是概率统计中的应用所观察到的现象对有关概率分布的主观判断(即先验概率)进行修正的标准方法。
所谓贝叶斯法则,是指当分析样本大到接近总体数时,样本中事件发生的概率将接近于总体中事件发生的概率。
但行为经济学家发现,人们在决策过程中往往并不遵循贝叶斯规律,而是给予最近发生的事件和最新的经验以更多的权值,在决策和做出判断时过分看重近期的事件。
面对复杂而笼统的问题,人们往往走捷径,依据可能性而非根据概率来决策。
这种对经典模型的系统性偏离称为“偏差”。
由于心理偏差的存在,投资者在决策判断时并非绝对理性,会行为偏差,进而影响资本市场上价格的变动。
但长期以来,由于缺乏有力的替代工具,经济学家不得不在分析中坚持贝叶斯法则。
贝叶斯优化准则贝叶斯优化(Bayesian optimization)是一种用于优化目标函数的迭代式方法,其目标是在尽可能少的迭代次数内找到函数的全局最优解或局部最优解。
贝叶斯优化通过在参数空间中建立目标函数的后验模型,并使用这个模型来指导下一步的参数选择,以在每次迭代中寻找最有希望的参数值。
以下是贝叶斯优化的几个关键要素和步骤:1.先验模型:贝叶斯优化首先需要选择一个先验模型来表示目标函数的未知性质。
通常采用高斯过程(Gaussian Process, GP)作为先验模型,因为它能够提供目标函数的一个联合分布的先验估计。
2.采样:在初始阶段,通过在参数空间中随机采样来收集一些观察数据点。
这些数据点用于拟合高斯过程的初始参数,从而构建目标函数的后验模型。
3.建模:基于初始采样数据,使用高斯过程拟合目标函数的后验模型。
高斯过程会给出目标函数在每个参数点的概率分布,包括均值和方差。
4.选择下一个采样点:利用后验模型,通过一种称为采样策略(Acquisition Function)的方法来选择下一个最有希望的参数值。
采样策略通常会权衡探索未探索区域(Exploration)和利用已知信息(Exploitation)之间的平衡,以在参数空间中找到最可能包含最优解的区域。
5.观察:根据采样策略选择的参数值,观察目标函数在该点的实际值,并将这个观察结果添加到已有的数据集中。
6.更新模型:使用新的观察数据,更新高斯过程的参数,进而更新目标函数的后验模型。
这样就可以在下一轮迭代中更准确地预测目标函数在参数空间中的行为。
7.重复迭代:重复以上步骤,直到达到预设的停止条件,如达到最大迭代次数、收敛到一个满意的解或达到预设的目标精度为止。
贝叶斯优化的主要优点之一是能够在相对较少的迭代次数内找到全局最优解或局部最优解,尤其在参数空间维度较高、目标函数计算代价较高的情况下效果显著。
其核心思想是通过在参数空间中动态地收集观察数据并更新模型,来逐步地探索和优化目标函数的全局形状。