杠杆的基础计算题复习课程
- 格式:doc
- 大小:322.00 KB
- 文档页数:18

杠杆平衡状态复习题带答案杠杆平衡状态是物理学中一个重要的概念,它涉及到力和力臂的平衡。
以下是关于杠杆平衡状态的复习题及答案。
题目一:定义题请简述什么是杠杆的平衡状态。
答案:杠杆的平衡状态是指杠杆处于静止或匀速转动的状态,此时杠杆上作用的所有力矩之和为零。
题目二:计算题在一个杠杆系统中,已知力F1=200N,力臂L1=0.5m,另一端的力F2=500N,力臂L2=2m。
请计算杠杆是否处于平衡状态,并求出未知力的大小。
答案:根据杠杆平衡条件,力矩平衡公式为 \( F1 \times L1 = F2\times L2 \)。
代入已知数值,\( 200N \times 0.5m = 500N \times L2 \),解得 \( L2 = 0.2m \)。
由于L2小于2m,所以杠杆处于平衡状态,未知力的大小为 \( F2 = 500N \)。
题目三:判断题如果一个杠杆的两端分别挂有重量不同的物体,且杠杆处于平衡状态,那么这两个物体的重量之比一定等于它们到支点的距离之比。
答案:正确。
根据杠杆平衡条件,物体的重量(力)和它们到支点的距离(力臂)的乘积必须相等,即 \( m1g \times d1 = m2g \times d2 \),其中\( m \)是质量,\( g \)是重力加速度,\( d \)是到支点的距离。
因此,\( \frac{m1}{m2} = \frac{d2}{d1} \)。
题目四:应用题一个小孩在玩跷跷板,他的质量为40kg,坐在距离支点2m的位置。
如果要保持跷跷板平衡,一个质量为60kg的大人应该坐在距离支点多远的位置?答案:首先计算小孩对杠杆的力矩,\( 40kg \times 9.8m/s^2\times 2m = 784Nm \)。
设大人到支点的距离为 \( d \) 米,大人对杠杆的力矩为 \( 60kg \times 9.8m/s^2 \times d \)。
根据平衡条件,\( 784Nm = 60kg \times 9.8m/s^2 \times d \),解得 \( d\approx 1.3m \)。

初中杠杆试题讲解教案教学目标:1. 知识与技能:通过讲解和练习,使学生掌握杠杆的基本概念、杠杆的平衡条件以及杠杆的应用。
2. 过程与方法:培养学生运用杠杆原理解决实际问题的能力。
3. 情感、态度和价值观:激发学生对物理学科的兴趣,培养学生的探究精神。
教学重点:1. 杠杆的基本概念:支点、动力、阻力、动力臂、阻力臂。
2. 杠杆的平衡条件:F1L1 = F2L2。
3. 杠杆的应用:剪刀、钳子、撬棍等。
教学难点:1. 杠杆平衡条件的理解和应用。
2. 判断动力臂和阻力臂的长度。
教学准备:1. 教具:杠杆模型、剪刀、钳子、撬棍等。
2. 教学材料:PPT、黑板、粉笔。
教学过程:一、导入(5分钟)1. 谈话:同学们,你们在生活中见过哪些杠杆?它们是如何工作的?2. 学生回答:剪刀、钳子、撬棍等。
3. 教师总结:今天我们就来学习杠杆的基本原理和应用。
二、讲解杠杆的基本概念(10分钟)1. 讲解支点、动力、阻力、动力臂、阻力臂的定义。
2. 示例:剪刀、钳子、撬棍等,指出它们的支点、动力、阻力、动力臂、阻力臂。
三、讲解杠杆的平衡条件(15分钟)1. 讲解杠杆的平衡条件:F1L1 = F2L2。
2. 示例:剪刀剪东西时,如何判断力的大小关系?3. 学生练习:判断钳子、撬棍等工具在使用过程中,力的大小关系。
四、讲解杠杆的应用(10分钟)1. 讲解剪刀、钳子、撬棍等工具的原理和应用。
2. 学生练习:设计一个简单的杠杆系统,验证杠杆的平衡条件。
五、试题讲解(15分钟)1. 讲解历年中考中的杠杆题目,分析解题思路和方法。
2. 学生练习:解答给出的杠杆题目。
六、总结(5分钟)1. 回顾本节课所学内容,引导学生总结杠杆的基本概念、平衡条件和应用。
2. 强调杠杆在生活中的重要性,激发学生的学习兴趣。
教学反思:本节课通过讲解和练习,使学生掌握了杠杆的基本概念、平衡条件以及应用。
在讲解过程中,注意引导学生通过实际例子去理解和应用杠杆原理,提高了学生的学习兴趣和动手能力。





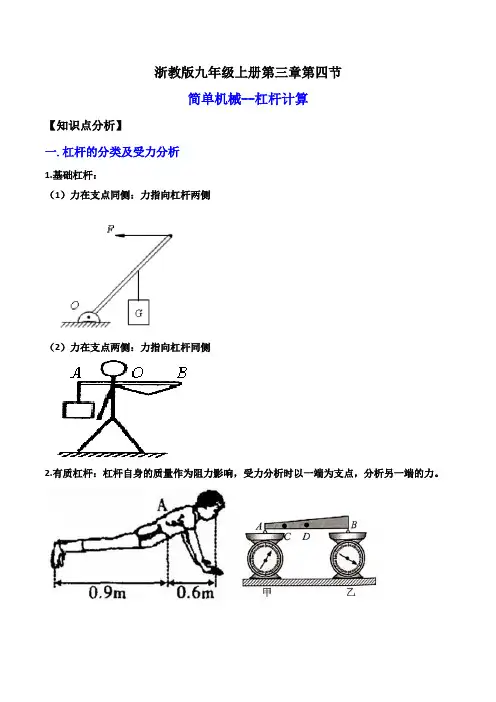
浙教版九年级上册第三章第四节简单机械--杠杆计算【知识点分析】一.杠杆的分类及受力分析1.基础杠杆:(1)力在支点同侧:力指向杠杆两侧(2)力在支点两侧:力指向杠杆同侧2.有质杠杆:杠杆自身的质量作为阻力影响,受力分析时以一端为支点,分析另一端的力。
3.多杠杆:在进行受力分析时发现一个杠杆的力在另一个杠杆有着相反的作用效果时,即为多个杠杆结合使用4.多力臂:对于同一个杠杆,有着多个力共同作用得到一个平衡的效果,或原已平衡的杠杆动态分析5.结合类杠杆:杠杆结合浮力进行受力分析,杠杆与压力压强结合,按照杠杆平衡原理和基础受力分析一起结合解题【例题分析】一、选择题1.小明用独轮车搬运砖头,车箱和砖头的总质量是120kg ,独轮车的有关尺寸如图所示,下列说法正确的是( )A .独轮车是费力杠杆B .动力臂是90cmC .阻力臂是0.3mD .匀速推车时,人手竖直向上的力F 是400N 【答案】C【解析】ABC .由图可知,支点在车轮的轴上,力F 为动力,所以动力臂的长度 L 1 =90cm+30cm=120cm=1.2m 阻力是G ,阻力臂的长度 L 2 =30cm =0.3mA .1︰4B .4︰1C .1︰5D .5︰1【答案】C【解析】如图所示,根据杠杆平衡条件1122Fl F l =可得AC G AB F ⨯=⨯,已知CB =4AC ,则动力F 跟物重G 之比为155F AC AC ACG AB AC CB AC ====+A .②③B .①④C .②③④D .①③【答案】A【解析】①杠杆左端悬挂质量为2kg 的A 物体,如图乙所示,L 1︰L 2=2︰1,由杠杆平衡条件可得12L mg L F ⨯=解得B 端绳对杠杆的拉力 1222kg 10N/kg=40N L F mg L =⨯=⨯⨯ 则B 对地面的压力变化了40N ,由Fp S=可得,B 的底面积 322230610Pa 40N 1m 100210c Pa m F S p -⨯-⨯∆====∆ 故①错误;②若A 物体的质量增加1kg ,B 端绳对杠杆的拉力 ()()12221kg 10N/kg=60N L F m m g L ''=⨯+=⨯+⨯ B 静止时对地面的压力为 322B B 610Pa 10m 60N=F p S F -'==⨯⨯=此时B 物体对地面的压强恰好为0,故②正确;③若移动支点O 的位置,使L 1︰L 2=3︰1时,由杠杆平衡条件 12L mg L F ''⨯= 解得B 端绳对杠杆的拉力 1232kg 10N/kg=60N L F mg L ''=⨯=⨯⨯ B 物体恰好被拉离地面,故③正确;④若图中B 物体竖直切割15并拿走,B 对地面的压力为 BB 48N 5F F F '=⨯-= B 对地面的压强为 B B228N800Pa 10mF p S -''=== B 对地面的压强变为切割前的0.4倍,故④错误; 综上,A 正确,BCD 错误。



杠杆及其计算考点一:杠杆1.定义:在力的作用下能绕着固定点转动的硬棒。
杠杆可以是直的,亦可以是弯的,硬棒理解为不可变形的棒。
2.杠杆有关的名词(1)杠杆绕着转动的固定点叫支点,用符号O表示。
(2)使杠杆转动的力叫动力,用符号F1表示。
(3)阻碍杠杆转动的力叫阻力,用符号F2表示。
(4)从支点到动力作用线的距离叫动力臂, 用符号l1表示。
(5)从支点到阻力作用线的距离叫阻力臂, 用符号l2表示。
注意:动力和阻力的方向并不一定相反,但动力和阻力的作用效果一定是相反的,动力和阻力可以在支点的两侧,也可以在支点的同侧。
(同侧异向,异侧同向)3.力臂的画法:一定点 (支点),二划线 (力的作用线),三从点 (支点)向线 (力的作用线)引垂线,支点到垂足的距离即为力臂,标上相应的符号。
注意:力臂必定过支点,注意作图时用虚线大括号或者实线箭头。
考点二:杠杆平衡条件1.杠杆平衡的定义 :在力的作用下 ,如果杠杆处于静止状态或绕支点匀速转动,我们就说杠杆平衡了。
注意杠杆平衡并不是必须杠杆水平。
2.探究杠杆平衡条件的实验实验步骤:①调节杠杆两端的平衡螺母,使杠杆在不挂钩码时,保持水平并静止,达到平衡状态。
②在杠杆两侧挂上不同数量的钩码,通过改变钩码的位置或数量,使杠杆重新在水平位置平衡。
③测量多组数据。
实验方法:控制变量法【注意】①调节杠杆时,要使杠杆在水平位置平衡,主要是为了便于直接从杠杆上读出力臂;②利用弹簧测力计方向要始终沿竖直方向。
③实验过程中,不能再调节平衡螺母。
④实验至少做三次,防止实验结果的偶然性。
3. 杠杆的平衡条件动力×动力臂=阻力×阻力臂;即F1l1=F2l2,这个平衡条件是阿基米德发现的,被称为杠杆原理。
4.作图根据杠杆平衡条件考点三:杠杆分类分类结构特征特点应用举例省力杠杠动力臂大于阻力臂省力、费距离撬棒、铡刀、动滑轮、羊角锤、钢丝钳、手推车、花枝剪刀等费力杠杆动力臂小于阻力臂费力、省距离缝纫机踏板、理发剪刀、钓鱼竿、起重臂等等臂杠杆动力臂等于阻力臂不省力不费力天平、定滑轮注意:判断杠杆类型需要结合生活实际考虑此杠杆的目的是省力还是省距离,然后判断是省力杠杆还是费力杠杆。
1.用一撬棍撬石头,石头对棍的阻力为1000N ,动力臂为150cm,阻力臂为15cm,求人所用的力。
N N F F cmcm l l F F :10010001.01.01.015015211221=⨯=====可得解2.已知动力臂是阻力臂的20倍,阻力为20000牛,只需几牛的动力就可以克服阻力?N N F F l l F F :100020000201201201211221=⨯====可得解3.一重为1000N 的重物挂在杠杆支点左侧20厘米处,小明最多只有500N 的力气,在支点右侧30厘米处能否使利用杠杆举起重物,如不能,还要将杠杆加长多少厘米?cmcm cm l cm N cm N F GL l Gl l F ,cm N cm N 10304040500201000,20100030500121211=-==⨯===⨯<⨯加可得根据所以小明不能举起重物4.有一横截面是长方形的重物,横截面长宽比为4:3,重物重为1000N ,要使其沿支点转动,至少要几牛的动力?N N l Gl F Gl Fl 。
,l ,,,:400521000221453412212=⨯====⨯=可得由动力最小臂最大沿对角线方向拉时动力重力的力臂由图可知线长为根据勾股定理可知对角则宽为设长方形长为解5.有一杠杆,动力臂为20厘米,阻力臂为5厘米,用40的力,能克服多大的对杠杆的阻力?6.OB 为轻质杠杆,OA=60cm ,AB=20cm 。
在杠杆的B 端挂一个所受重力为60N 的重物,要使杠杆在水平位置上平衡,在A 点加一个多大的竖直向上的拉力?N cm cm cm N OAOB G F OB G OA :F 8060)2060(60=+⨯=⨯=⨯=⨯得解7.如图是一台手动小水泵的示意图。
当竖直向下作用在手柄OB 的力F 1为40牛顿时,水泵提起一定量的水,手柄长OB=50厘米,这时它与水平面夹角为300,阻力臂长OC=14厘米。
求:(1)动力臂L 1;(2)这时提起水的重量G 。
8.如图是建筑工地搬运泥土的独轮车,车身和泥土的总重力G =1200牛。
要在A 点用最小的力抬起独轮NN F F cm cm l l F F 160404441205121221=⨯=====得由N cm cm N L FL G GL FL cm cm OB L :7.123143.4340)2(3.43502323)1(21211=⨯====⨯=⨯=得解车,此力的方向应是竖直向上、大小为300牛。
(写出计算过程)9.轻质杠杆的支点为O ,力臂OA =0.2m ,OB =0.4m.在A 端挂一体积为10-3m 3的物体,B 端施加一竖直向下、大小为10N 的拉力,杠杆恰能在水平位置平衡。
求:①物体所受重力; ②物体的密度(g =10N/kg )。
10.某人用一根轻质木棒挑一重为120牛的物体站在水平地面上,木棒AB 保持水平,棒长AB=1.2米,重物悬挂处离肩膀距离BO=0.8米,则人的肩膀对木棒的支持力为360牛。
若肩膀与B 端的距离变小,则肩膀的支持力将变小(填“变大”、“变小”或“不变”)。
[ 提示,为了保持杠杆平衡,手得给杠杆一个向下的压力。
]11.灯重30 N ,灯挂在水平横杆的C 端,O 为杠杆的支点,水平杆OC 长2 m ,杆重不计,BC 长0.5 m ,绳子BD 作用在横杆上的拉力是多少?(∠DBO=30°)3333/10210/1020)2(202.04.010)1(m Kg m Kg N N gV G V m N mm N OA OB F G OA G OB F ⨯=⨯====⨯=⨯=⨯=⨯-ρ得解N cm cm N OA OC G F OC G OA F cm OA OA ,4050214010050=⨯⨯=⨯=⨯=⨯=得由根据勾股定理可知力臂为通过作图可知最大的动12.将质量为10kg 的铁球放在不计重力的木板OB 上的A 处,木板左端O 处可自由转动,在B 处用力F 竖直向上抬着木板,使其保持水平,已知木板长1m ,AB 长20 cm ,求F 的大小.13.为了保证起重机在起重时不会翻倒,起重机右边配有一个重物M.现测得重物M的质量为4t ,AB为10m ,BC为4m ,CD为1m .(g=10N /㎏) 问:该起重机可起吊的最大物重为多少?(起重机本身的重不计)14.直角轻棒ABO ,可绕O 点自由转动,AB=30厘米,OB=40厘米,现在OB 中点C 处挂一重物G=100牛,欲使OB 在与墙面垂直的位置上保持平衡,则在A 点至少应加多大的力?Ncm cm cm N OB OA G F OA G OB F NKg N Kg mg G 80100)20100(100100/1010:=-⨯=⨯=⨯=⨯=⨯==得由解Nmm m N AB BD G G BD G AB G N Kg N Kg mg G B 2000010)14(4000040000/10400021212=+⨯=⨯=⨯=⨯=⨯==得由最大物重点即将摔倒时的物重为起重机摔倒时的支点是的方向竖直向下使的作用点得向右移动所以可得由方向竖直向上得由则令解211221122122634)2(42111232121)1(:,F OA ,F N F OB F OA OB F OA F 。
N ,N OBOA F F OB F OA F ,OB AB ,OA ==⨯=⨯=⨯=⨯=+⨯=⨯=⨯=⨯=+===15.一轻质杠杆可绕O 点转动,在杠杆的A 点和B 端分别作用两个力F 1、F 2,已知OA :AB=1:2.求 ①若F 1=12牛,方向竖直向下,为使杠杆保持水平平衡,求作用在B 端的力F 2的最小值和方向。
②若F 1减为6牛,方向变为竖直向上,若不改变上题中F 2的大小,又如何使杠轩在水平位置平衡。
16.如图,AB是一个质量不计的杠杆,支点为O,杠杆AB两端分别挂有甲、乙两个物体,杠杆平衡,已知甲物体的质量是1.5千克,乙物体的质量为4.5千克,AB长2米,则支点O应距A点多少米。
(g=10N/Kg)17.轻杆AB 可绕支点O 自由转动,A 端所悬挂的物体重640牛。
站在水平地面上重500牛的人用竖直向下的力拉轻杆的B 端,此时轻杆AB 在水平位置上平衡,如图所示。
如果BO=2AO ,人的一只鞋的鞋底面积为180cm 2,则人对B 点的拉力为多少 ? 此人对地面的压强是多少?F 1 .5.1,5.1,231315.45.1:m A O m OA m OB OA ,OA OB OA OB G G Kg Kg m m g m g m G G 点离所以支点解得又因为所以根据杠杆平衡条件可知由解乙甲乙甲乙甲乙甲==+======33434341418122,12,81,81.02.0:PS g V G G G F G F A G G G F OA OB G F G G V V g V g V G G Vg mg G A A A A A A A A B A B A A B B A B A B A ===-=-==⨯===========ρρρρ对地面的压力由杠杆的平衡条件可知所以由于解法二18如图所示,杠杆在水平位置平衡, A.B 为同种材料制成的正方体,边长分别为0.2m 和0.1m ,且已知OA:OB=1:2,物体A 对地面的压强为6000pa ,则A 的密度为多少?Pa m N S F P N N N F G F N N G F AO BO F G B A B B A 5000101802180180320500320264022:24=⨯⨯===-=-======-人对地面的压力得由解333332/104/)1.022.0(10240)2()2(222240)2.0(60002:m Kg m Kg V V g F V V g g V g V gm g m G G F G F N m Pa PS F A G OAOB G F OB G OA F B A B A B AB A B A A A A B B A B A ⨯=⨯-⨯=-=-=-=-=-=-==⨯===⨯=⨯=⨯ρρρρ所以对地面的压力为得由解Pa mN S F P A N N N F G F A N cm cm cm N OA OC G F OA OC G F ,C B N N N F F G N cm cm N OA OB G F ,OA OB G F ,N m Pa PS F A A A B A B A A A B A B A 400010300120120120240120201030602409015090203060150103005000:2424=⨯===-=-==+⨯=⨯===+=+==⨯=⨯===⨯⨯==--对地面的压强此时对地面的压力此时物体得由杠杆也处于静止平衡处时挂在当物体所以因为杠杆平衡对地面的压力物体解:由杠杆平衡条件可得解19.如图所示,杠杆在水平位置平衡,OA=20厘米,OB=30厘米,BC=10厘米,物体A 的底面积为300厘米2,物体B 重60牛,地面对物体A 的压强为5000帕,如果将挂物体B 的悬点移至C 点,此时地面对物体A 的压强为多少帕?20.如图,O为杠杆AB的支点,OA:OB=2:3,物块甲和物块乙分别挂在杠杆的A、B两端,杠杆平衡,已知物块甲、物块乙的体积之比是2:1,物块甲的密度ρ甲=6×103千克/米3,物块乙的密度ρ乙是多少。
4.如图所示装置中,O为轻质杠杆AB支点,AO:OB=3:2,A端用细绳连接物体M,B端用细绳悬挂物体N,物体N浸没在水中,此时杠杆恰好在水平位置平衡。
已知物体N的体积为5×10﹣4m3,物体N 的密度为4×103kg/m3,g取10N/kg,绳子的重力忽略不计。
求:(1)物体N的质量m N;(2)物体N所受的浮力F N;(3)物体M的重力G M。
5.如图所示,小明爷爷的质量为m=60kg,撬棍长BC=1.2m,其中O为支点,OB=AC=0.2m。
当小明爷爷用力F1作用于A点时,恰能撬动重为G1=1200N的物体。
g取10N/kg,求:(1)作用力F1的大小;(2)保持支点位置不变,F1的方向保持不变,小明爷爷所能撬动的最大物体重G m。
6.如图所示,一根轻质直杠杆在水平位置保持平衡,左端挂100牛的物体G1,其力臂L1为0.6米,右端挂200牛的物体G2,求:(1)右端物体G2的力臂L2。
(2)若在右端增加200牛的物体,要使杠杆再次水平平衡,支点应向哪端移动多少距离。
7.如图所示的轻质杠杆,0A=30厘米,OB的长度为20厘米,若挂在B点物体重力为30牛。