全等三角形判定复习 PPT(公开课)

N 明方法与前题基本相同,只
须证明⊿ABN≌⊿BCM
A
C
B
变式4:如图,⊿ABD,⊿ACE都是正三角形, 求证CD=BE
D
A
E
B
C
分析:此题实质上是把题目中的条件B,A,C三点改为 不共线,证明方法与前题基本相同.
变式6:如图,分别以⊿ABC的边AB,AC为一边 画正方形AEDB和正方形ACFG,连结CE,BG.
求证BG=CE
E
分析:此题是把两个三
角形改成两个正方形而
D
A
G 以,证法类同
FBBiblioteka C小结:1.证明两个三角形全等，要结合题目的条件 和结论，选择恰当的判定方法
2.全等三角形，是证明两条线段或两个角相 等的重要方法之一，证明时
①要观察待证的线段或角，在哪两个可能全等的三 角形中。
②分析要证两个三角形全等，已有什么条件，还缺 什么条件。
AB=CB
A
AD=CD
BD=BD
_
=
P
∴ △ABD≌△CBD(SSS)
B
D
∴∠ABD=∠CBD
_
=
在△ABP和△CBP中
C
AB=BC
∠ABP=∠CBP
BP=BP
∴ △ABP ≌ △CBP(SAS)
∴PA=PC
例4。已知:如图AB=AE,∠B=∠E，BC=ED AF⊥CD 求证：点F是CD的中点
分析：要证CF=DF可以考虑CF 、 DF所在的两个三角形全等，为此可 添加辅助线构建三角形全等 ，如何 添加辅助线呢?
知识结构图
性质
全等三角形对应边相等 全等三角形对应角相等
全 全等 等三 形角
形

例2(2023金华):如图,
A,E,B,D在同一直线上,
AB=DE,AC=DF,AC ∥ DF,
在ΔABC和ΔDEF,
(1)
求证: ΔABC≌ΔDEF;
F
AB=DE(已知) ∠A=∠D(已证) AC=DF (已知) ∴ΔABC≌ΔDEF(SAS)
A
E
B
D
C
经典例题:
证明:∵AC=2DB,AE=EC (
B
准备条件 指出范围 列举条件 得出结论
例讲解1：
如图，已知AD∥ BC，AD=BC.你能阐明△ABC与 △CDA全等吗？你能阐明AB=CD，AB∥CD吗？ 为何?
证明：∵ AD∥ BC，（已知）
∴ ∠DAC=∠BCA。
D
C
（两直线平行，内错角相等）
在△ADC和△CBA中，
∵ AD=BC（已知）
A B
A
C
2 1
B
D
E
C
第2题
D
想一小想明：旳设计方案：先在池塘旁取一种能 如直图接线到段达AAB和是B处一旳种点池C塘，连旳结长A度C并，延长至
目D前点想，测使A量C这=D个C池，塘连结旳B长C并度延，长在至E点，
水使上BC测=量EC不，以连便结，ED你，有用什米尺么测好出旳DE旳长， 措这施个较长以度便就地等于把A池，塘B两旳点长旳度距测离量。请你阐 出明来理吗由？。想想看。AC=DC
D
C A
∴∠B＝∠C（全等三角形
相应角相等）
B
DE C
3.如图，∠B＝∠E，AB＝EF，BD＝
EC，那么△ABC与 △FED全等吗？ F
为何？ AC∥FD吗？为何？
C 42
B 13 D

例子1：如图，在△AEC和△ADB中，已 知AE=AD，AC=AB，请说明△AEC ≌ △ADB的理由。
解：在△AEC和△ADB中
C
_A_E__=__A_D_(已知)
D
∠A= ∠A( 公共角)
A
E
B
_A_C___=_A__B_(已知)
∴ △AEC≌△ADB（ SAS ）
例2：如图，AC=BD，∠CAB= ∠DBA，
第十二章 全等三角形
三角形全等的判定（3）
— ASA AAS
一、知识梳理: 三角形全等判定方法1
三边对应相等的两个三角形全等（可以简写
为“边边边”或“SSS”）。
A
用符号语言表达为：
在△ABC和△ DEF中
B
C
AB=DE
D
BC=EF
CA=FD
∴ △ABC ≌△ DEF（SSS） E
F
例1：如图．△ＡＢＣ是一个钢架，ＡＢ＝ＡＣ， ＡＤ是连接Ａ与ＢＣ中点Ｄ的支架．
1O
B
2
∠A= ∠B (已知）
D OA=OB (已证）
∠1= ∠2 (对顶角相等） ∴ △AOC≌△BO（ASA）
例2： 已知：点D在AB上，点E在AC上，BE 和CD相交于点O,AB=AC, ∠B= ∠C
求证： ∴△ADC≌△AEB AD=AE.
证明：在△ADC和△AEB中
A
∠A= ∠A (公共角）
∴ Rt△ACB≌Rt△ADB (HL). ∴BC=BD
(全等三角形对应边相等).
小结
一般三角形 全等的识别 S.S.S S.A.S A.S.A A.A.S 直角三角形 H.L 全等的识别 灵活运用各种方法证明直角三角形全等

全等三角形的性质
1.全等三角形对应边相等，对应角相等
2.全等三角形的面积相等，周长相等 3.全等三角形对应边上的高线、中线、角 平分线分别相等
考点精炼
2、ＢＥ与ＣＤ相交于Ｏ，已知ＡＤ＝ＡＥ， ∠ＡＤＣ＝∠ＡＥＢ，图中有几对全等三角 形，说明理由。
Ａ
△ AEB ≌ △ADC （ASA）
Ｂ
Ｄ
Ｏ
2图
Ｅ Ｃ
Ａ Ｄ Ｂ Ｃ
SAS
1图
Ｅ
考点精炼
2、ＢＥ与ＣＤ相交于Ｏ，已知ＡＤ＝ＡＥ，∠ＡＤＣ＝ ∠ＡＥＢ，图中有几对全等三角形，说明理由。
Ａ
△BOD≌ △COE （AAS）
Ｂ
Ｄ
Ｏ
2图
Ｅ Ｃ
考点精炼
1、ＢＥ与ＣＤ相交于Ｏ，已知ＡＤ＝ＡＥ，∠ＡＤＣ＝ ∠ＡＥＢ，图中有几对全等三角形，说明理由。
Ａ △BDC≌ △CEB
A Eห้องสมุดไป่ตู้B
O
D
F
C
二：利用全等三角形证明线的垂直关系
例：如图：BF是Rt△ABC的角平分线，∠ACB=90°， CD是高，BF与CD交于点E，EG∥AC交AB于G 求证：FG⊥AB
证明：∵BF平分∠ABC
A G F
C 3 E 4 D 1 2 B
∴∠1＝∠2 ∵CD⊥AB ∴∠3+∠ABC=90° ∴BG=BC （全等三角形的对应边相等） 又 ∵∠ACB＝90° ∴∠A+∠ABC=90° 在△BFG与△BFC中 ∴∠3＝∠A BG=BC 又∵EG∥AC ∠1＝∠2 ∴∠A＝∠4 BF=BF ∴∠3＝∠4 ∴△BFG≌△BFC （SAS） 在△BEG与△BEC中 ∠1＝∠2 ∴∠FGB=∠FCB=90° ∠3＝∠4 （全等三角形的对应角相等） BE＝BE ∴FG⊥AB ∴△BEG≌△BEC （AAS）

7.如图（5）∠CAE=∠BAD，∠B=∠D，
AC=AE，△ABC与△ADE全等吗？为什么？
B
解：∵ ∠CAE=∠BAD(已知)
E
D
∴ ∠CAE+∠BAE=∠BAD+∠BAE
C
A
(等量加等量，和相等) 即∠BAC=∠DAE
在△ABC和△ADE中，
∠B=∠D(已知)
∠BAC=∠DAE(已证)
AC=AE(已知)
典型例题:
例1 :如图,点B在AE上, ∠CAB=∠DAB,要使 ΔABC≌ΔABD,可补充的 一个条件是∠ACB=B=∠AEA=DC∠D.BEA
C
A
B E
D
分析：现在我们已知 A→∠CAB=∠DAB
S→ AB=AB(公共边) .
①用SAS,需要补充条件 AB=AC, ②用ASA,需要补充条件 ∠CBA=∠DBA, ③用AAS,需要补充条件 ∠C=∠D, ④此外,补充条件 ∠CBE=∠DBE也可以(?)
要使△ABD≌△ACD， • 根据“SAS”需要添加条件 AB=AC ； • 根据“ASA”需要添加条件∠BDA=∠CDA • 根据“AAS”需要添加条件 ∠B=∠C
D
C
； ；
友情提示：添加条件的题目.首先要 找到已具备的条件,这些条件有些是 题目已知条件 ,有些是图中隐含条件.
8
认 识 到 了 贫 困户贫 困的根 本原因 ，才能 开始对 症下药 ，然后 药到病 除。近 年来国 家对扶 贫工作 高度重 视，已 经展开 了“精 准扶贫 ”项目
12
D
E
M
N
B
C
创造条件！ ？ 6
认 识 到 了 贫 困户贫 困的根 本原因 ，才能 开始对 症下药 ，然后 药到病 除。近 年来国 家对扶 贫工作 高度重 视，已 经展开 了“精 准扶贫 ”项目

1 A
2
下列条件:①A①BA=BA=EA,②E
D
BC=ED,③∠C=∠D,④
在ΔABC和ΔAED中
∠B=∠E,其中能使
AC=AD
ΔABC≌ΔAED的条件有
∠BAC=∠EAD
( )个. A.4 B.3 C.2 D.1
AB=AE
∴ΔABC≌ΔAED(SAS)
可编辑课件PPT
12
C
E
例2 (2006湖北十堰):如图, 已知∠1=∠2,AC=AD,增加 B
1 A
2
下列条件:①AB=AE,②
D
BC=ED,③∠C=∠D,④
在ΔABC和ΔAED中
∠∠BB=∠=∠EE,其, 中能使
AC=AD
ΔABC≌ΔAED的条件有
∠BAC=∠EAD
( )个.
A.4 B.3 C.2 D.1
∠B=∠E
∴ΔABC≌ΔAED(AAS)
可编辑课件PPT
15
例3 (2007金华):如图,
AB=A’B’
BC=B’C’
B
C B’
C’
AC=A’C’
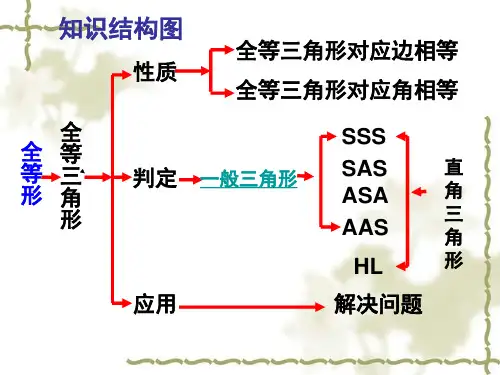
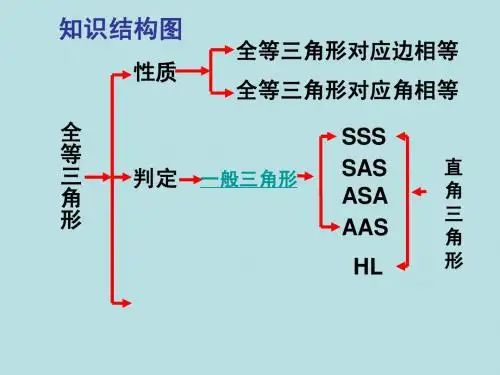
全等三角形对应边相等，对应角相等
可编辑课件PPT
3
三、全等三角形的判定
1、判定1：两边和它们的夹角对应 相等的两个三角形全等。简称“边 角边 ”（SAS）。 2、判定2：两角和它们的夹边对应 相等的两个三角形全等。简称“角 边 角”（ASA）
可编辑课件PPT
16
∵AB=CD(已知) ∴ AB+BC=CD+BC, 即
AC=BD.
知,AB=CD,CE=DF,AE=BF, 在ΔACE和ΔBDF中
则AE∥BF吗?为A 什么?

复习目的与意义
加深对全等三角形判 定定理的理解和掌握
为后续学习相似三角 形、三角函数等知识 点打下基础
2024/1/29
提高运用全等三角形 判定定理解决问题的 能力
4
复习内容与范围
01
02
03
04
全等三角形的定义和性 质
2024/1/29
全等三角形的五种判定 方法：SSS、SAS、ASA、 AAS、HL
角边角（ASA）和角角边（AAS） 判定法
2024/1/29
14
角边角（ASA）和角角边（AAS）判定法原理
角边角（ASA）原理
两个三角形中，如果两个角及它们所 夹的一边分别相等，那么这两个三角 形全等。
角角边（AAS）原理
两个三角形中，如果两个角及其中一个 角的对边分别相等，那么这两个三角形 全等。
2024/1/29
应试技巧指导
总结中考中解答全等三角 形相关问题的应试技巧， 如审题、画图、标注和检 查等。
模拟试题训练
提供针对中考的全等三角 形模拟试题，进行实战演 练和巩固提高。
25
07
总结回顾与展望未来
2024/1/29
26
பைடு நூலகம்
本次复习内容总结回顾
全等三角形的定义和性质
全等三角形是指两个三角形在形状和大小上完全相同。全等三角形的对应边相等，对应角相 等。
2024/1/29
解决问题的策略
掌握观察、分析、归纳和猜想等解 决问题的基本策略，并能够灵活运 用。
创新思维的培养
通过一题多解、多题一解和变式训 练等方式，培养创新思维和发散性 思维。
24
历年中考真题解析与应试技巧指导
中考真题解析

好的△ ′′′剪下来，放到△ 上，它们全等吗？
画一个△ ′′′，使′′ = ，′’ =
，∠′ = ∠：
（1）画∠′ = ∠；
（2）在射线′上截取′′ = ，在
射线′上截取′′ = ；
（3）连接′′.
【结论】两边和它们的夹角分别相等的三角形全等。也就是说，三角形的两
⫽ .
∠4. 求证：∠5 = ∠6.
∵ ∠1 = ∠2，∠3 = ∠4， = ，
根据易证△ ≌△ ，
∴有 = ，
又∵ ∠3 = ∠4， = ，
则可根据判定△ ≌△ ，
故∠5 = ∠6.
知识梳理
例4：如图，、交于点，、为上两点， = ， =
就全等了.如果满足斜边和一条直角边分别相等，这两个直
角三角形全等吗？
教学新知
探索5：任意画出一个△，使∠=90°.再画一个 △ ′’’，使
∠′=90°，′′=，′′=.把画好的△′′′剪下来，放
到△上，它们全等吗？
画 一 个 △ ′′′ ， 使 ∠′ = 90° ， ′′ =
求证 = .
∵⊥，⊥
∴∠与∠都是直角
在R △ 和Rt △ 中，
=
=
∴ △ ≌ △ （）
∴ = .
知识梳理
知识点1：“边边边”（或“SSS”）
1.三边分别相等的两个三角形全等（可以简写成“边边边”
两个三角形全等吗？上述六个条件中，有些条件是相关的.
能否在上述六个条件中选择部分条件，简捷地判定两个三角
形全等呢？
探索1：先任意画出一个△ ABC.再画一个△ A′B′C′，使△ ABC与
△ A′B′C′满足上述六个条件中的一个（一边或一角分别
相等）或两个（两边、一边一角或两角分别相等）.你

例、如图，已知AB=AC，AD=AE，AB、DC相交
于点M，AC、BE相交于点N，∠1=∠2，试说明：
（1） △ABE ≌ △ACD （2）AM=AN A
12
D
E
M
N
B
C
创造条件！ ？
7
一、挖掘“隐含条件”判全等
AD
1.如图（1），AB=CD，AC=BD，则
△ABC≌△DCB吗?说说理由
B 图（1） C
E
D
∴ ∠CAE+∠BAE=∠BAD+∠BAE
C
A
(等量加等量，和相等) 即∠BAC=∠DAE
在△ABC和△ADE中， ∠B=∠D(已知) ∠BAC=∠DAE(已证)
AC=AE(已知)
12
∴△ABC≌ △ADE (AAS)
典型例题:
例6 :如图,已知,AB=CD, CE=DF,AE=BF, 则AE∥DF吗?为什么?
第4讲 全等三角形的判定
1
知识点
定义：能够
的两个三角形
全 等
对应元素：对应_____、对应
三 性质：全等三角形的对应边
角 形
全等三角形的
、
、对应 。
、
。
也对应相等。
判定： 、
、
、
。
全等三角形的画图:
利用直尺和圆规，根据 、 、 的
方法都可画出与已知三角形全等的三角形。
2
三角形全等的4个种判定公理：
AC=DC
A
B
∠ACB=∠DCE
BC=EC
C
△ACB≌△DCE(SAS)
E
D
AB=DE
16
典型例题:
例8 :如图在 ΔABC中, AD⊥BC于D,BE⊥AC 于E,AD交BE于F, 若BF=AC,那么∠ABC 的大小是( )

课堂小结
边角边公理 角边角公理 边边边公理 角角边公理
作业：课本P115 1~8
小结
为了规范事业单位聘用关系，建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ，保障 用人单 位和职 工的合 法权益
角角边公理（AAS）
有两角和其中一角的对边对 应相等的两个三角形全等
小结
课前热身
已知：如图，AB=DC，AD=BC. 求证： ∠A= ∠C.
例1
已知：如右图，AB、CD相交于点O， AC∥DB,OC = OD, E、F为 AB上两点，
且AE = BF. 求证：CE=DF.
A
C
E
F
D
.
例2
A
如右图， 已知：AB=AD，CB=CD.
求证：AC⊥BD.
B
O
D
C
已知：△ABC的顶点和△DBC 的顶点A和D在BC的同旁, AB =DC, AC = DB, AC和DB相交 于点O.
求证：OA =OD.
练习一
继再 续接 学再 习厉 新， 知让 识我 吧们
教学重难点
教学重点：能让学生选择适当判定方法 判定两三角形全等。
教学难点：培养学生有条理的分析、推 理能力，并写出证明过程。
前面的知识你忘记了吗？
让我们一起来 复习一下吧
我们学过几种三角形的全等判定呢？（4种）
边角边公理 角边角公理 边边边公理 角角边定理
为了规范事业单位聘用关系，建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ，保障 用人单 位和职 工的合 法权益
为了规范事业单位聘用关系，建立和 完善适 应社会 主义市 场经济法权益

注意事项
在证明过程中，需要注意两边和所夹 的角分别相等的条件必须同时满足， 且所夹的角必须是两边的夹角，否则 不能得出全等的结论。
角边角（ASA）判定定理证明
基本思路
证明方法
注意事项
如果两个三角形有两个角和它们的夹边 分别相等，则这两个三角形全等。
可以通过构造法或者余弦定理来证明。 构造法可以构造出两个三角形，然后通 过证明它们有两个角和夹边分别相等来 得出它们全等的结论。余弦定理可以通 过三角形的边角关系来证明两个三角形 有两个角和夹边分别相等，从而得出它 们全等的结论。
注意事项
在证明过程中，需要注意两个角和其 中一个角的对边分别相等的条件必须 同时满足，否则不能得出全等的结论。 同时，AAS和ASA的区别在于所给的条 件不同，但都可以用来判定两个三角 形是否全等。
04
全等三角形的应用举例
Chapter
在几何证明中的应用
证明线段相等
通过证明两个三角形全等，可以推出它们对应的边相等，从而证 明线段相等。
全等三角形的判定ppt课件完整版
目录
• 引言 • 全等三角形的判定方法 • 全等三角形判定定理的证明 • 全等三角形的应用举例 • 实验操作与探究 • 全等三角形判定的拓展与延伸
01
引言
Chapter
三角形的定义与性质回顾
三角形的定义
由不在同一直线上的三条线段首尾顺 次相接所组成的图形。
三角形的分类
在证明过程中，需要注意两个角和夹边 分别相等的条件必须同时满足，且所夹 的边必须是两个角的夹边，否则不能得 出全等的结论。
角角边（AAS）判定定理证明
基本思路
证明方法
如果两个三角形有两个角和其中一个 角的对边分别相等，则这两个三角形 全等。