当前位置：文档之家 › 全等三角形的判定一课件.ppt

全等三角形的判定一课件.ppt

  • 格式：ppt
  • 大小：650.00 KB
  • 文档页数：18

下载文档原格式

  / 18

合集下载

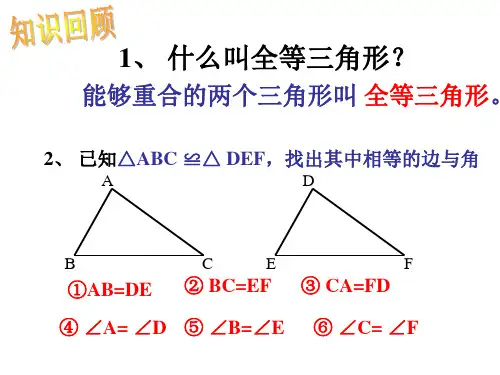
三角形全等的判定一课件

三角形全等的判定一课件

1
B
2
A D C
E
小结
1.学习了本节课以后,你有哪些收获? 2.你还有什么疑惑?
作业
课本90页,练习第1,2题 习题15.2 2
思考
学习本节课后,我们知道已知两边及其夹角这三对 元素对应相等,就可以判断两三角形全等,那么两个三 角形具备其他三组元素对应相等,他们是否也能得到 两个三角形全等?
∵ ∠DAC＝∠BCA(已证) AC＝CA(公共边)
∴△ADC≌△CBA(SAS)
B
准备条件 指出范围 列举条件 得出结论
证明的书写步骤：
①准备条件：证全等时要用的间接 条件要先证好；
②三角形全等书写三步骤： 写出在哪两个三角形中 摆出三个条件用大括号括起来 写出全等结论
活动二
下列图形中,若用SAS证两个三角形全等,至少还需 要添加什么条件?
D
A
B
C
如果AB之间不能直接测量,你能测出AB之 间的距离吗?
范例学习
例2 如图,在湖泊的岸边有A、B两点，难以直接量出A、 B两点间的距离，你能设计一种量出A、B两点之间距离 的方案吗？说明你这样设计的理由。
A
B’
C
B A’
解:在岸上取可以直接到达A,B的一点C,连接AC,延长AC到点A’,使A’C=AC;连接BC到 点B’,使B’C=BC.连接A’B’,量出A’B’的长度. 由于△ABC≌△A’B’C’(SAS),所以AB=A’B’(全等三角形的对应边相等)因而,A’B’的长度 就是A,B两点之间的距离.
根据三角形的内角和为180度，则第三角一定确定， 所以当三内角对应相等时，两个三角形不一定全等
两个条件 一个条件 ①两角； ①一角； ②两边；

全等三角形判定ppt课件

全等三角形判定ppt课件

若两个三角形全等，则它们的周长也 相等。
对应角相等
在全等三角形中，任意两个对应 的角都相等。
若两个三角形全等，则它们的内 角和也相等，且均为180度。
可以通过测量两个三角形的三个 内角来判断它们是否全等。
面积相等
若两个三角形全等，则它们的面积也相等。 可以通过计算两个三角形的面积来判断它们是否全等。
1 2
定义
两边和它们的夹角分别相等的两个三角形全等。
图形语言
若a=a'，∠B=∠B'，b=b'，则⊿ABC≌⊿A'B'C'。
3
符号语言
∵a=a'，∠B=∠B'，b=b'，∴⊿ABC≌⊿A'B'C'（ SAS）。
角边角判定法（ASA）
01
02
03
定义
两角和它们的夹边分别相 等的两个三角形全等。
图形语言
实例1
证明两个三角形全等并求出未知 边长
实例2
利用全等三角形判定方法证明两个 四边形面积相等
实例3
利用全等三角形判定方法解决一个 实际问题，如测量一个不可直接测 量的距离
06
总结与展望
判定全等三角形的方法总结
三边分别相等的两个三角形全等。这是最基本的判定 方法，通过比较三角形的三边长度来确定两个三角形
证明过程
可以通过AAS（角角边）全等条件进行证明，即 如果两个三角形有两个角和其中一个角的对边分 别相等，则这两个三角形全等。这也是一种常用 的全等三角形判定方法。
实际应用举例
在实际应用中，角角边判定法常用于解决与角度 和边长有关的问题。例如，在建筑设计中，如果 需要确保两个建筑结构的角度和边长完全相等， 就可以利用角角边判定法来进行验证。

人教版《三角形全等的判定》PPT全文课件

人教版《三角形全等的判定》PPT全文课件
知识回顾
问题探究
课堂小结
随堂检测
活动2
0
探究一：探索三角形全等的条件
建立模型，探索发现
只给定一条边相等：
只给定一个角相等：
3cm
3cm
3cm
30°
30°
30°
满足一个条件相等时，两个三角形不一定全等.
知识回顾
问题探究
课堂小结
随堂检测
活动3
0
探究一：探索三角形全等的条件
问题：两个三角形满足六个条件中的两个条件，两个三角形全等吗？两个条件有几种情况?
证明：连接AC，
【解题过程】
如图, 在四边形ABCD中, AB=AD, CB=CD, 求证:∠B=∠D.
∴∠B=∠D．(全等三角形对应角相等)
【思路点拨】先连接AC, 由于AB=AD, CB=CD, AC=AC, 利用SSS可证△ABC≌△ADC, 于是∠B=∠D. 要求学生从“形”思维到“质”的思维飞跃, 实现将“文字语言”, “图形语言”转化为“符号语言”.
∥
∵BC=DE, ∴BC+CD=DE+CD. 即BD=CE.
【数学思想】 数形结合思想，分类讨论思想.
∴ ∠ADB＝∠FEC，AD=EF (全等三角形对应角相等) ∴AD∥EF(同位角相等，两直线平行)
在△ABD和△FCE中
∴△ABD≌△FCE (SSS).
知识回顾
问题探究
课堂小结
随堂检测
例4
0
探究三：利用三角形全等的判定“SSS”解决问题
△ABC是一个钢架，AB=AC，AD是连接点A与BC中点D的支架，请问AD⊥BC吗？请说明理由．
在△ABD和△ADC中，
∴△ABD≌△ACD (SSS).

三角形全等的判定ppt课件

三角形全等的判定ppt课件

知4－讲
1. 基本事实：两角和它们的夹边分别相等的两个三角形全 等(可以简写成“角边角”或“ASA”).
感悟新知
2. 书写格式：如图12 . 2-8， 在△ ABC 和△ A′B′C′ 中， ∠ B= ∠ B′， BC=B′C′， ∠ C= ∠ C′， ∴△ ABC ≌△ A′B′C′( ASA).
第十二章 全等三角形
12.2 三角形全等的判定
感悟新知
知识点 1 基本事实“边边边”或“SSS”
知1－讲
1. 基本事实：三边分别相等的两个三角形全等(可以简写成 “边边边”或“SSS”). 这个基本事实告诉我们：当三角形的三边确定后， 其形状、大小也随之确定. 这是说明三角形具有稳定性的 依据.
感悟新知
感悟新知
知5－练
例5 如图12.2-11，AB=AE，∠ 1= ∠ 2，∠ C= ∠ D． 求证：△ ABC ≌△ AED．
感悟新知
思路引导：
知5－练
感悟新知
知5－练
技巧点拨：判定两个三角形全等，可采用执果 索因的方法，即根据结论反推需要的条件. 如本 题还缺少∠ BAC= ∠ EAD，需利用已知条件∠ 1= ∠ 2 进行推导.
感悟新知
知2－练
③以点M′为圆心，以MN 长为半径作弧，在∠ BAC 内 部交②中所画的弧于点N′； ④过点N′作射线DN′交BC 于点E． 若∠ B=52°，∠C=83°，则∠ BDE= ___4_5_°__.
感悟新知
知识点 3 基本事实“边角边”或“SAS”
知3－讲
1. 基本事实：两边和它们的夹角分别相等的两个三角形全 等(可以简写成“边角边”或“SAS”).
感悟新知
解：∵∠BAD＝∠EAC， ∴∠BAD＋∠CAD＝∠EAC＋∠CAD， 即∠BAC＝∠EAD.

完整版三角形全等的判定ppt课件

完整版三角形全等的判定ppt课件
12.5 三角形全等的判定
初二（5、6）班
1
1、 什么叫全等三角形？
能够重合的两个三角形叫 全等三角形。
2、 已知△ABC ≌△ DEF，找出其中相等的边与角
A
D
①AB=DE ④ ∠A= ∠D
② BC=EF ⑤ ∠B=∠E
③ CA=FD ⑥ ∠C= ∠F
B
CE
F
全等三角形性质：
全等三角形的对应边相等，对应角相等。
40
例 如图，有一池塘，要测池塘两端A、B的距离，
可先在平地上取一个不经过池塘可以直接到达点A 和B
的点C，连接AC并延长至D，使CD =CA，连接BC 并延
长至E，使CE =CB，连接ED，那么量出DE的长就是A，
B的距离．为什么？
A
B
1
C
2
E
D
41
证明：在△ABC 和△DEC 中，
AC = DC（已知），
(4) 两角一边 ?
27
3.角边角公理(ASA)：
两角和它们的夹边分别相等的两个三角形全等.简 写成“角边角”或“ASA ”
A
几何语言：
在△ABC 和△ A′B′ C′中，
B
∠A =∠A′
AB = A′B′
∠B =∠B′
∴ △ABC ≌△ A′B′ C′（ASA）． B′
C A′
C′
28
4.角角边公理(AAS)：
AB =AC ，
∵ BD =CD ， B
D
C
AD =AD ，
∴ △ABD ≌ △ACD （ SSS ）．
32
证明的书写步骤：
①准备条件：证全等时要用的条件要先证好； ②三角形全等书写三步骤：

直角三角形全等的判定.ppt

直角三角形全等的判定.ppt

⑵ 在射线C´M上取段B´C´=BC;
⑶ 以B´为圆心,AB为半径画弧，交 射线C´N于点A´; ⑷ 连接A´B´. 现象： 两个直角三角形能重合。 说明： 当一个直角三角形的一条直角边和 斜边确定后， 那么它的形状和大小 也被确定.
∟ ∟
M
B´ B´
C´ ´
判定公理：
有斜边和一条直角边对应相等的 条件1 条件2
∟ C´
M
B´
亲自实践
把你所画的三角形撕出来， 与原三角形进行比较，看是否 能重合？
请你动手画一画
任意画出一个Rt△ABC,∠C=90°。再画 一个Rt△A´B´C´，使得∠C´= 90°， B´C´=BC，A´B´= AB。
按照下面的步骤画一画 ⑴ 作∠MC´N=90°; B
A
∟ C N A´ A´
SA 可判定全等； 则利用 A AS 可判定全等； 则利用 A AS 可判定全等；
则利用 A
AS 可判定全等；
⑤若测得AC=DE，∠A=∠D，AB=DE，
AS
可判定全等；
情境问题2:
A D
B
C
E
F
如果工作人员只带了一条皮尺，能 完成这项任务吗？
情境问题2:
工作人员是这样做的，他测量了每个三角 形没有被遮住的直角边和斜边， 发现它们分 对于两个直角三角形，若满足 别对应相等，于是他就肯定“两个直角三角 一条直角边和一条斜边对应相等时， 形是全等的”。你相信他的结论吗？ 这两个直角三角形全等吗？ A
通过刚才的探索，发现工作人员 的做法 是完全正确的。
两个直角三角形全等.
前提
直角三角形全等的判定方法：
斜边和一条直角边对应相等的两个直角三角 形全等. 简写：“斜边、直角边”或 “HL” A' A

《三角形全等的判定》全等三角形PPT课件

《三角形全等的判定》全等三角形PPT课件
好的△ ′′′剪下来，放到△ 上，它们全等吗？
画一个△ ′′′，使′′ = ，′’ =
，∠′ = ∠：
（1）画∠′ = ∠；
（2）在射线′上截取′′ = ，在
射线′上截取′′ = ；
（3）连接′′.
【结论】两边和它们的夹角分别相等的三角形全等。也就是说，三角形的两
⫽ .
∠4. 求证：∠5 = ∠6.
∵ ∠1 = ∠2，∠3 = ∠4， = ，
根据易证△ ≌△ ，
∴有 = ，
又∵ ∠3 = ∠4， = ，
则可根据判定△ ≌△ ，
故∠5 = ∠6.
知识梳理
例4：如图，、交于点，、为上两点， = ， =
就全等了.如果满足斜边和一条直角边分别相等，这两个直
角三角形全等吗？
教学新知
探索5：任意画出一个△，使∠=90°.再画一个 △ ′’’，使
∠′=90°，′′=，′′=.把画好的△′′′剪下来，放
到△上，它们全等吗？
画 一 个 △ ′′′ ， 使 ∠′ = 90° ， ′′ =
求证 = .
∵⊥，⊥
∴∠与∠都是直角
在R △ 和Rt △ 中，
=
=
∴ △ ≌ △ （）
∴ = .
知识梳理
知识点1：“边边边”（或“SSS”）
1.三边分别相等的两个三角形全等（可以简写成“边边边”
两个三角形全等吗？上述六个条件中，有些条件是相关的.
能否在上述六个条件中选择部分条件，简捷地判定两个三角
形全等呢？
探索1：先任意画出一个△ ABC.再画一个△ A′B′C′，使△ ABC与
△ A′B′C′满足上述六个条件中的一个（一边或一角分别
相等）或两个（两边、一边一角或两角分别相等）.你

全等三角形的判定PPT课件共34张

全等三角形的判定PPT课件共34张
24
2024/1/30
06
判定全等三角形的注意事项
25
准确理解全等三角形的定义和性质
2024/1/30
全等三角形的定义
两个三角形如果三边及三角分别对应 相等，则称这两个三角形全等。
全等三角形的性质
全等三角形的对应边相等，对应角相 等；全等三角形的周长、面积相等； 全等三角形的对应边上的中线、高线 、角平分线分别相等。
结论
三边分别相等的两个三角 形全等，简称“SSS”。
16
SAS判定法的证明
已知条件
两边和它们的夹角分别相 等的两个三角形。
2024/1/30
证明过程
将其中一个三角形旋转至 与另一个三角形两边重合 ，由于夹角相等，因此两 个三角形全等。
结论
两边和它们的夹角分别相 等的两个三角形全等，简 称“SAS”。
示例
若三角形ABC和三角形DEF中，∠A=∠D，∠B=∠E ，BC=EF，则三角形ABC全等于三角形DEF。
2024/1/30
14
2024/1/30
04
判定方法的证明与推导
15
SSS判定法的证明
01
02
03
已知条件
三边分别相等的两个三角 形。
2024/1/30
证明过程
通过平移或旋转其中一个 三角形，使得两个三角形 的三边分别重合，从而证 明两个三角形全等。
2024/1/30
在计算三角形面积时，如果知道两个三角形全等，那么可以直接得出它们的面积相 等。
9
2024/1/30
03
全等三角形的判定方法
10
边边边判定法（SSS）
定义
三边分别相等的两个三角形全等 。

《三角形全等的判定》-完整版课件

《三角形全等的判定》-完整版课件
观察这些图片，你能看出形状、大小完全一样的几 何图形吗？
你能再举出生活中的一些类似例子吗？
请同学们把一块三角尺按在纸板上， 画下图形后，比较观察这两个三角形 有何关系？从同一张底片冲洗出来的 两张尺寸相同的照片上的图形，放在 一起也能够完全重合吗？
全等三角形的概念
全等三角形： 能够完全重合的两个三角
全等三角形对应角相等．
B
C
请说出目前判定三角形全 等的4种方法：
SAS，ASA，AAS，SSS
问题 任意画一个Rt△ABC，使∠C =90°，再画 一个Rt△A＇B＇C＇，使∠C＇=90°，B＇C＇=BC， A＇B＇=AB，然后把画好的Rt△A＇B＇C＇剪下来放到 Rt△ABC上，你发现了什么？
F
C
B
E
L
从上面的图形中可以看出，若已知 ∠A=60°，∠B=80°，相信你一 定可以求出△ABC的各个角的大小： ∠D=__6_0_°_，∠E=_8_0_°_， 40° ∠F=___．
已知：如图，△ABC ≌△DEF． （1）若DF =10 cm，则AC 的长为 10 cm ； （2）若∠A =100°，则：
C1
比眼力：找全等．
8
Ⅰ 30o
9
8Ⅱ 30o
5
8 30o
8Ⅲ
5 30o
Ⅴ 8
8Ⅵ 30o8
8 Ⅶ
30o 9
Ⅳ8 5
8 Ⅷ
5
如图，有一池塘，为测量池塘两端A、B的距
离，设计了如下方案：如图，先在平地上取 一个可直接到达A、B的点C，再连结AC、
BC并分别延长AC至D、BC至E，使CD=CA，
CE=CB，最后测得DE的距离即为AB的 长．你知道其中的道理吗？

三角形全等的判定ppt课件

三角形全等的判定ppt课件
追问1：这个尺规作图的方法利用了上节课中的哪个知识点？
追问2：根据前面的操作，你能探究到什么结论？
例1. 如图，有一池塘，要测池塘两端A、B的距离，可先在平 Nhomakorabea上取一个可以
直接到达A和B的点C，连接AC并延长到D，使CD＝CA，连接BC并延长到E，
使CE＝CB．连接DE，那么量出DE的长就是A、B的距离，为什么?
如图，两根长度为12米的绳子，一端系在旗杆上，另一端分别固定在地面两
个木桩上，两个木桩离旗杆底部的距离相等吗？
解：BD=CD
在Rt△ABD 和 Rt△ACD 中，
AB=AC
AD=AD

∴Rt△ABD≌Rt△ACD(HL)
∴ BD=CD
例1.如图，AC⊥BC，BD⊥AD，AC =BD．求证：BC =AD．
（1）
AD = BC
（ HL ）；
（2）
AC = BD
（ HL ）；
（3） ∠DAB = ∠CBA
（ AAS ）；
（4） ∠DBA = ∠CAB
（ AAS ）．
D
A
C
B
对于两个直角三角形，除了直角相等的条件，还要满足几个条件，这两个三
特殊方法
角形就全等了？
HL定理
SSS
一
般
方
法
SAS
AAS
AAS
直角三角形全等
问题:三角分别相等的两个三角形全等吗？
追问:证明两个三角形全等的方法有哪些？
评价3.如图，AB⊥BC，AD⊥DC，垂足分别为B，D，∠1=∠2.
求证：AB=AD.
∵AB⊥BC，AD⊥DC，
∴∠B=∠D=90°，
在△ABC和△ADC中，

13.3 全等三角形的判定 - 第1课时课件(共18张PPT)

13.3 全等三角形的判定 - 第1课时课件(共18张PPT)
使用几何拼接条探究三个元素相等的三角形是否全等？1.用绿色、蓝色、橙色拼条为边长作2个三角形，把两个三角形比较，它们能重合吗？2.用红色、蓝色、黄色拼条为边长作2个三角形，把两个三角形比较，它们能重合吗？
三角相等：
三边相等：
基本事实一
如果两个三角形的三边对应相等，那么这两个三角形全等.
基本事实一可简记为“边边边”或“SSS”.
拓展提升
1.如图，已知AB=AE，AD=AC，BC=ED，BC，DE交于点O.求证：∠BAD=∠EAC.
证明：在△BAC和△EAD中，AB＝AE，AC＝AD，BC＝ED．∴△BAC≌△EAD（SSS）．∴∠BAC=∠EAD.∴∠BAC－∠DAC=∠EAD－∠DAC，即∠BAD=∠EAC.
归纳小结
能够完全重合的两个三角形叫做全等三角形.
全等三角形的性质：全等三角形的对应边相等，对应角相等.
探究一
新知探究
知识点1 边边边
通过作图探究一个元素相等能否判定两个三角形全等？
一条边相等：
一个角相等：
探究二
通过几何拼接条探究两个元素相等的三角形是否全等？
两条边相等：
两个角相等：
一边一角相等：
探究三
探究四
知识点2 三角形的稳定性
用拼接条制作三角形和四边形框架,并拉动它们，你发现了什么？
三角形的形状和大小是固定不变的，而四边形的会改变.
三角形所具有的这一性质叫做三角形的稳定性.四边形具有不稳定性.
在生活中，我们经常会看到应用三角形稳定性的例子.
在生活中，我们也经常会看到应用四边形不稳定性的例子.
随堂练习
1.已知：如图，AB=EF，AC=ED，BF=CD.求证：∠A=∠E.
证明：∵BF=CD，∴BF+FC=CD+FC∴BC=FD∵AB=EF，AC=ED∴△ABC≌△EFD（SSS）∴∠A=∠E.

《三角形全等的判定》课件

《三角形全等的判定》课件
《三角形全等的判定》
知识回顾
1.什么叫全等三角形？
能够完全重合的两个三角形叫做全等三角形.
A
2.三边分别相等的两个三角形全等(可以
简写成“边边边”或“SSS”).
符号语言表示：在△ABC和△A'B'C'中，B
C
AB=A'B'，
A'
AC=A'C'，
BC=B'C'，
∴△ABC≌△A'B'C' (SSS). B'
C'
3.两边和它们的夹角分别相等的两个三角形全等（可以
简写成“边角边”或“SAS”）.
A
符号语言表示：在△ABC和△A′B′C′中，
AB=A′B′， ∠B=∠B′， BC=B′C′，
B
C
A'
∴△ABC≌△A′B′C′(SAS). B'
C'
4.两角和它们的夹边分别相等的两个三角形全等（可以
简写成“角边角”或者“ASA”）.
FE
BE=CF，
A
B
∴Rt△ABE≌Rt△DCF（HL）. ∴AE=DF.
随堂练习
1.已知，在Rt△ABC和Rt△A′B′C′中，∠C=∠C′=90〫，
有如下几个条件：①AC=A′C′，∠A=∠A′；②AC=A′C′， AB=A′B′；③AC=A′C′，BC=B′C′；④ AB=A′B′，
∠A=∠A′.其中，能判定Rt△ABC≌Rt△A′B′C′的条件的
需寻找的条件
可证直角与已知锐角的夹边对 应相等或者与锐角（或直角）
的对边对应相等
可证一直角边对应相等或证一 锐角对应相等
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

三角形的一个内角为30 ,一条边为3cm
30◦ 3cm
30◦ 3cm
30◦ 3cm
如果三角形的两个内角分别是30 ,50 时
30◦
50◦
30◦
50◦
如果三角形的两边分别为4cm，6cm 时
4cm 6cm
4cm 6cm
30◦ 3cm
30°
只给两个条
件作出三角
30◦ 3cm
30◦ 3cm
形，不能保
已知：△ABC 求作：△DEF,使DE=AB,∠E=∠B,EF=BC 将所作的△DEF与△ABC叠一叠，看看它们是否完全 重合？由此你能得到什么结论？
A
B
C
全等三角形判定方法一(基本事实)
两边和它们的夹角对应相等的 两个三角形全等。简记为“边角 边”或“SAS”(S表示边，A表示 角）。
范例学习
B
C 应边相等)
小结：
1.今天我们经历了画图验证两个三角形全等的过程， 探索出两个三角形全等的方法之一“两边和它们的夹角对 应相等的两个三角形全等”，我们可以利用它来判别两个 三角形是否全等。
2.我们可以通过证明三角形全等的方法来证明线段相 等或角相等。
３.证明两个三角形全等的思路：首先分析条件，观 察已经具备了什么条件，然后以已具备的条件为基础，根 据全等三角形的判定方法，来确定还需要证明哪些边或角 对应相等，再设法证明这些边和角相等。
例3 (2006湖北黄冈):如图, (已知) ∴DDBB==EECC 又∵ AC∥ DB(已知)
AC∥ DB, AC=2DB,E是AC ∠D∠BDEB=E∠=C∠ECBEB(两直线平行,
的中点,求证:BC=DE
内错角相等)
A
∵BBEE==EEBB(公共边)
∴ ΔDBE≌ΔCEB(SAS) ∴
D
E
BC=DE (全等三角形的对
14.2 三角形全等的判定 （一）
问题引入
小伟作业本上画的三角形被墨迹污染了， 他想画一个与原来完全一样的三角形，他该 怎么办？请你帮助小伟想一个办法，并说明 你的理由？
注意：与原来完全一样的三 角形，即是与原来三角形全 等的三角形。
想一想： 要画一个三角形与小伟画的三角形全等。
需要知道几个与边或角的大小有关的条件？ 只知道一个条件（一角或一边）行吗？两个 条件呢？三个条件呢？
证所画出的
三角形一定
50°
30°
50° 全等。
4cm 6cm
6cm 4cm
（1）三边相等 （2) 三角相等 （3）两边一角(两边和它们的夹角；两边和其中一边 的对角） （4）两角一边（两角和它们的夹边；两角和其中一角 的对边）
我们今天专题研究有两条边和它们的夹角对应相等的 两个三角形是否全等？
做一做：
例:已知:如图,AD∥BC AD＝BC
D
求证: △ADC≌△CBA
A
证明:∵AD∥BC(已知) ∴∠DAC＝∠BCA(两直线平行,内错角相等) 在△ADC和△CBA中, AD＝BC(已知) ∠DAC＝∠BCA(已证) AC＝CA(公共边) ∴△ADC≌△CBA(SAS)
C
B
准备条件 指出范围
列举条件 得出结论
想一解想：：先在池塘旁取一个能直接到达A和B 如处图的线点段C，AB连是结一AC个并池延塘长的至D长点度，，使 现A在C=想D测C，量连这结个BC池并塘延的长长至度E点，，在使BC=EC， 水连上结测ED量，不测方出便DE，的你长有，这什个么长好度的就等于A，
方B法两点较的方距便离地。把池塘的长度测量
出来吗？想想看。
AC=DC
B
∠ACB=∠DCE
A
BC=EC
C
△ACB≌△DCE(SAS)
D
AB=DE（全等三角形的对应边相等）
E
例题讲解1：
如图，已知AD∥ BC，AD=BC.你能说明△ABC与△CDA全 等吗？你能说明AB=CD，AB∥CD吗？为什么?
证明：∵ 等）
AD∥ BC，（已知）
D
C
∴ ∠DAC=∠BCA。
让我们一个 △ A’B’C’，使△ A’B’C’满足 上述六个条件中的一个或两个，你画 出的△ A’B’C’与△ A’B’C’全 等吗？
做一做：
（1）只给出一个条件（一条边或一个角） 画三角形时，画出的三角形一定全等吗？
3cm 45◦
3cm
3cm
45◦
45◦
（2）给出两个条件画三角形时，有几种可能 的情况？每种情况下作出的三角形一定全等吗？
按下面的条件画三角形，画完后小组内交流， 看所画的三角形是否全等。(其它条件不确定） 1)三角形的一个内角为30°，一条边为3cm; 2) 三角形的两个内角分别为30°和45°; 3）三角形的两条边分别为4cm和6cm.
（两直线平行，内错角相等）
在△ADC和△CBA中，
∵ AD=BC（已知）
A
B
∠DAC=∠BCA （已证）
AC=CA（公共边）
∴ △ABC≌△CDA（SAS）
∴ AB=CD(全等三角形的对应边相等）
∠BAC=∠DCA （全等三角形的对应角相
∴ AB∥CD(内错角相等，两直线平行）
典型例题:
证明:∵AC=2DB,AE=EC