濮良贵机械设计第九版课后 习题答案.(DOC)

第三章 机械零件的强度习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ，取循环基数60105⨯=N ，9=m ，试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN3-2已知材料的力学性能为MPa260=s σ，MPa1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

[解] )170,0('A )0,260(C得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为：D =72mm ，d =62mm ，r =3mm 。

如用题3-2中的材料，设其强度极限σB =420MPa ，精车，弯曲，βq =1，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.14554==d D ，067.0453==d r ，查附表3-2，插值得88.1=ασ，查附图3-1得78.0≈σq ，将所查值代入公式，即查附图3-2，得75.0=σε；按精车加工工艺，查附图3-4，得91.0=σβ，已知1=q β，则根据()()()29.60,67.141,0,260,34.72,0D C A 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ，应力幅MPa 20a =σ，试分别按①C r =②Cσ=m ，求出该截面的计算安全系数ca S 。

[解] 由题3-4可知35.2,2.0MPa,260MPa,170s 1-====σσK Φσσ（1）C r =工作应力点在疲劳强度区，根据变应力的循环特性不变公式，其计算安全系数 （2）C σ=m工作应力点在疲劳强度区，根据变应力的平均应力不变公式，其计算安全系数第五章螺纹连接和螺旋传动习题答案5-5图5-49是由两块边板和一块承重板焊接的龙门起重机导轨托架。

第三章 机械零件的强度习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ，取循环基数60105⨯=N ，9=m ，试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσN MPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ，MPa 1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

[解] )170,0('A )0,260(C 012σσσΦσ-=- σΦσσ+=∴-1210 MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ 得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4圆轴轴肩处的尺寸为：D=72mm，d=62mm，r=3mm。

如用题3-2中的材料，设其强度极限σB=420MPa，精车，弯曲，βq=1，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.14554==dD，067.0453==dr，查附表3-2，插值得88.1=ασ，查附图3-1得78.0≈σq，将所查值代入公式，即()()69.1188.178.0111k=-⨯+=-α+=σσσq查附图3-2，得75.0=σε；按精车加工工艺，查附图3-4，得91.0=σβ，已知1=qβ，则35.211191.0175.069.1111k=⨯⎪⎭⎫⎝⎛-+=⎪⎪⎭⎫⎝⎛-+=qσσσσββεK()()()35.267.141,67.141,0,260,35.2170,0DCA∴根据()()()29.60,67.141,0,260,34.72,0DCA按比例绘出该零件的极限应力线图如下图3-5如题3-4中危险截面上的平均应力MPa20m=σ，应力幅MPa20a=σ，试分别按①C r =②C σ=m ，求出该截面的计算安全系数ca S 。

第三章 机械零件的强度习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ，取循环基数60105⨯=N ，9=m ，试求循环次数N分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσN MPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ，MPa 1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

[解] )170,0('A )0,260(C 012σσσΦσ-=-Θ σΦσσ+=∴-121MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-3一圆轴轴肩处的尺寸为：D =72mm ，d =62mm ，r =3mm 。

材料为40CrNi ，设其强度极限σB =900MPa ，屈服极限750MPa s σ=试计算周健的弯曲有效应力集中系数k σ。

[解] 因1.16D d =，0.048rd=，查附表3-2，插值得 1.995σα=，查附图3-1得78.0≈σq ，将所查值代入公式，即()()k 1110.78 1.9951 1.896σσσq α=+-=+⨯-=3-4圆轴轴肩处的尺寸为：D =54mm ，d =45mm ，r =3mm 。

如用题3-2中的材料，设其强度极限σB =420MPa ，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.14554==d D ，067.0453==d r ，查附表3-2，插值得88.1=ασ，查附图3-1得78.0≈σq ，将所查值代入公式，即()()69.1188.178.0111k =-⨯+=-α+=σσσq查附图3-2，得0.7σε=；按精车加工工艺，查附图3-4，得91.0=σβ，已知1=q β，则k 11 1.691111 2.510.70.911σσσσq K εββ⎛⎫⎛⎫=+-=+-⨯= ⎪ ⎪⎝⎭⎝⎭()()()170141.670,,260,0,141.67,2.512.51A C D ∴根据()()()0,67.73,260,0,141.67,56.44A C D 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ，应力幅MPa 20a =σ，试分别按①C r =②C σ=m ，求出该截面的计算安全系数ca S 。

第三章 机械零件的强度习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ，取循环基数60105⨯=N ，9=m ，试求循环次数N分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσN MPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ，MPa 1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

[解] )170,0('A )0,260(C 012σσσΦσ-=- σΦσσ+=∴-121MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-3一圆轴轴肩处的尺寸为：D =72mm ，d =62mm ，r =3mm 。

材料为40CrNi ，设其强度极限σB =900MPa ，屈服极限750MPa s σ=试计算周健的弯曲有效应力集中系数k σ。

[解] 因1.16D d =，0.048rd=，查附表3-2，插值得 1.995σα=，查附图3-1得78.0≈σq ，将所查值代入公式，即()()k 1110.78 1.9951 1.896σσσq α=+-=+⨯-=3-4圆轴轴肩处的尺寸为：D =54mm ，d =45mm ，r =3mm 。

如用题3-2中的材料，设其强度极限σB =420MPa ，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.14554==d D ，067.0453==d r ，查附表3-2，插值得88.1=ασ，查附图3-1得78.0≈σq ，将所查值代入公式，即()()69.1188.178.0111k =-⨯+=-α+=σσσq查附图3-2，得0.7σε=；按精车加工工艺，查附图3-4，得91.0=σβ，已知1=q β，则k 11 1.691111 2.510.70.911σσσσq K εββ⎛⎫⎛⎫=+-=+-⨯= ⎪ ⎪⎝⎭⎝⎭()()()170141.670,,260,0,141.67,2.512.51A C D ∴根据()()()0,67.73,260,0,141.67,56.44A C D 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ，应力幅MPa 20a =σ，试分别按①C r =②C σ=m ，求出该截面的计算安全系数ca S 。

第三章 机械零件的强度习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ，取循环基数60105⨯=N ，9=m ，试求循环次数N分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσN MPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ，MPa 1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

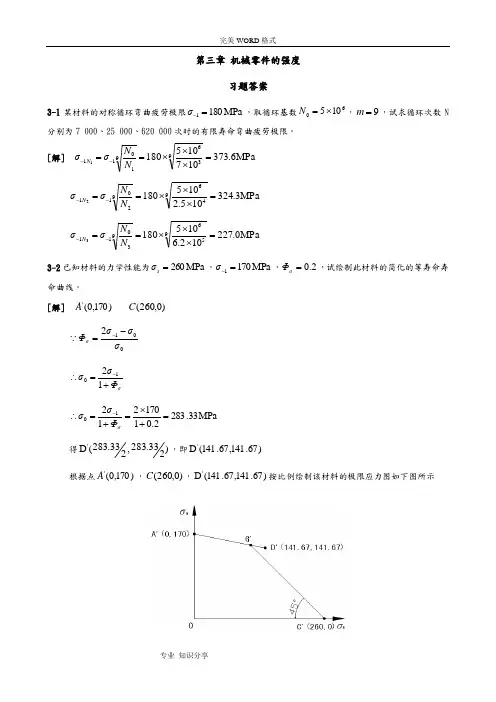
[解] )170,0('A )0,260(C 012σσσΦσ-=- σΦσσ+=∴-121MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-3一圆轴轴肩处的尺寸为：D =72mm ，d =62mm ，r =3mm 。

材料为40CrNi ，设其强度极限σB =900MPa ，屈服极限750MPa s σ=试计算周健的弯曲有效应力集中系数k σ。

[解] 因1.16D d =，0.048rd=，查附表3-2，插值得 1.995σα=，查附图3-1得78.0≈σq ，将所查值代入公式，即()()k 1110.78 1.9951 1.896σσσq α=+-=+⨯-=3-4圆轴轴肩处的尺寸为：D =54mm ，d =45mm ，r =3mm 。

如用题3-2中的材料，设其强度极限σB=420MPa ，试绘制此零件的简化等寿命疲劳曲线。

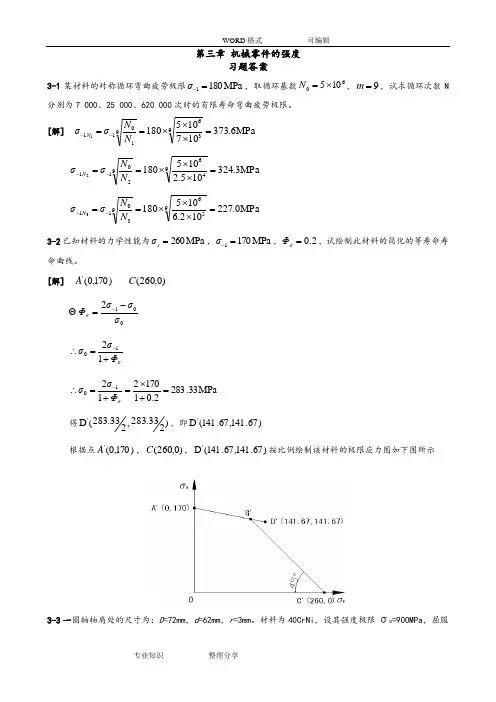
[解] 因2.14554==d D ，067.0453==d r ，查附表3-2，插值得88.1=ασ，查附图3-1得78.0≈σq ，将所查值代入公式，即()()69.1188.178.0111k =-⨯+=-α+=σσσq查附图3-2，得0.7σε=；按精车加工工艺，查附图3-4，得91.0=σβ，已知1=q β，则k 11 1.691111 2.510.70.911σσσσq K εββ⎛⎫⎛⎫=+-=+-⨯= ⎪ ⎪⎝⎭⎝⎭()()()170141.670,,260,0,141.67,2.512.51A C D ∴根据()()()0,67.73,260,0,141.67,56.44A C D 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ，应力幅MPa 20a =σ，试分别按①C r =②C σ=m ，求出该截面的计算安全系数ca S 。

第三章 机械零件的强度习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ，取循环基数60105⨯=N ，9=m ，试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσN MPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ，MPa 1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

[解] )170,0('A )0,260(C 012σσσΦσ-=- σΦσσ+=∴-121MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-3一圆轴轴肩处的尺寸为：D =72mm ，d =62mm ，r =3mm 。

材料为40CrNi ，设其强度极限σB =900MPa ，屈服极限750MPa s σ=试计算周健的弯曲有效应力集中系数k σ。

[解] 因1.16D d =，0.048rd=，查附表3-2，插值得 1.995σα=，查附图3-1得78.0≈σq ，将所查值代入公式，即()()k 1110.78 1.9951 1.896σσσq α=+-=+⨯-=3-4圆轴轴肩处的尺寸为：D =54mm ，d =45mm ，r =3mm 。

如用题3-2中的材料，设其强度极限σB=420MPa ，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.14554==d D ，067.0453==d r ，查附表3-2，插值得88.1=ασ，查附图3-1得78.0≈σq ，将所查值代入公式，即()()69.1188.178.0111k =-⨯+=-α+=σσσq查附图3-2，得0.7σε=；按精车加工工艺，查附图3-4，得91.0=σβ，已知1=q β，则k 11 1.691111 2.510.70.911σσσσq K εββ⎛⎫⎛⎫=+-=+-⨯= ⎪ ⎪⎝⎭⎝⎭()()()170141.670,,260,0,141.67,2.51 2.51A C D ∴ 根据()()()0,67.73,260,0,141.67,56.44A C D 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ，应力幅MPa 20a =σ，试分别按①C r =②C σ=m ，求出该截面的计算安全系数ca S 。

WORD 格式 可编写第三章 机械部件的强度习题答案3-1 某资料的对称循环波折疲倦极限σ1180MPa ，取循环基数 N 0 5 106 ， m 9 ，试求循环次数 N分别为 7 000 、 25 000 、 620 000 次时的有限寿命波折疲倦极限。

[ 解 ]σ1N 1σ1 9N 0 180 95 106373.6MPaN 17 103σ1N 2σ1 9 N 018095 106324.3MPaN 22.5 10 4σ1N 3σ19 N 018095 106227.0MPaN 36.2 10 53-2 已知资料的力学性能为 σs260MPa ， σ1 170MPa ， Φσ 0.2 ，试绘制此资料的简化的等寿命寿命曲线。

[ 解 ]A ' (0,170)C( 260,0)σ1σΦσ2 0σ0σ2σ11 Φσσ2σ1 2 170283.33MPa1 Φσ 1 0.2得 D '(283.332 ,283.332) ，即 D ' (141.67,141.67)依照点 A ' (0,170) ， C (260,0) ， D ' (141.67,141.67) 按比率绘制该资料的极限应力求以以下列图所示3-3 一圆轴轴肩处的尺寸为： D =72mm ， d =62mm ， r =3mm 。

资料为 40CrNi ，设其强度极限σB=900MPa ，信服WORD 格式可编写极限 σ750MPa 试计算周健的波折有效应力集中系数k 。

s[解] 因D1.16 ，r0.048 ，查附表 3-2 ，插值得σ1.995 ，查附图 3-1 得 q σ0.78 ，将所查值dd代入公式，即k σ 1 q σ σ 1 1 0.78 1.995 1 1.8963-4 圆轴轴肩处的尺寸为： D =54mm ， d =45mm ， r =3mm 。

如用题 3-2 中的资料，设其强度极限σ B=420MPa ，试绘制此部件的简化等寿命疲倦曲线。

西北工业大学蒲良贵主编《机械设计》新版第九版齿轮章节例题课堂讲解及习题解答（与原来第八版数表图均有不同）上海工程技术大学机械设计教研室陆宁编写sm n d v t /.311==1t226.2650.221==Fa Fa Y Ysa sa Y Y教材例题:试设计一对齿轮,输入功率P 1=10kw,小齿轮转速N1=960r/min,齿数比u=3.2,传动平稳,转向不变,c 齿轮相对于轴承为非对称布置.MPa H 540][1=σMPaH 523][2=σMPa F 57.303][1=σMPaF 86.238][2=σ初选Z1=24 Z2=77O14=β7级精度14634.901=d 2=m 4632.45/Z 11→==m d 圆整：以下不再赘述以下是教材计算题的解答过程10/29/201510-6 设计铣床中的一对直齿圆柱齿轮，已知P1=7.5kw ，n1=1450r/min,小齿轮相对于其轴的支撑为非对称布置，传动比要求u=2.08。

有轻微冲击，试设计这对齿轮。

补充条件：初选Kt=1.8 ，小齿轮齿数Z1=26，大齿轮齿数Z2=54.许用应力为：Mpa Mpa Mpa Mpa F F H 213][,220][,599][,600][2121H ====σσσσ补充作业（斜齿轮）前10-6习题中其他条件不变，按斜齿轮设计，初设螺旋角O 10=β8.10)625.2/(146/=⨯=h b 按轻微冲击，查表10-2得1.25K A =查图10-815.1=v K 查表10-34.1K K F ==ααH 查表10-43755.1=βH K 查图10-131.31K F =β载荷系数为：2.64k k K K K 2.77k k K K K F F V A F H H V A H ====βαβα查图10-2047.2=H z 钢材8.189=E z。

第三章机械零件的强度习题答案3-1某材料的对称循环弯曲疲劳极限，取循环基数，，试求循环次数N分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解]3-2已知材料的力学性能为，，，试绘制此材料的简化的等寿命寿命曲线。

[解]得，即根据点，，按比例绘制该材料的极限应力图如下图所示3-3一圆轴轴肩处的尺寸为：D=72mm，d=62mm，r=3mm。

材料为40CrNi，设其强度极限σB=900MPa，屈服极限试计算周健的弯曲有效应力集中系数。

[解] 因，，查附表3-2，插值得，查附图3-1得，将所查值代入公式，即3-4圆轴轴肩处的尺寸为：D=54mm，d=45mm，r=3mm。

如用题3-2中的材料，设其强度极限σB=420MPa，试绘制此零件的简化等寿命疲劳曲线。

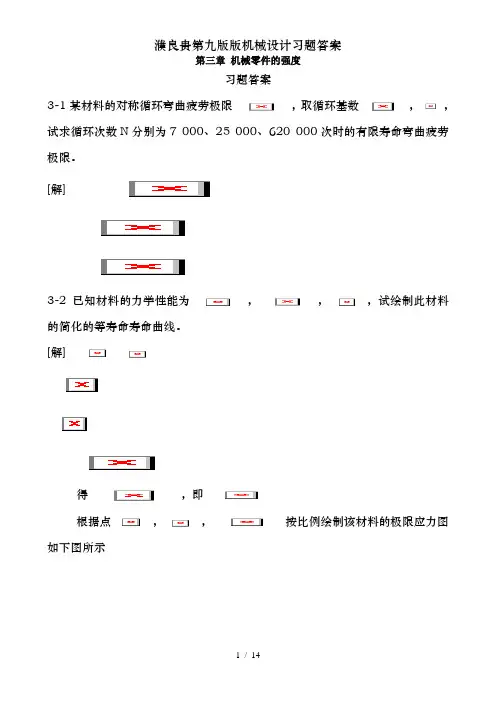
[解] 因，，查附表3-2，插值得，查附图3-1得，将所查值代入公式，即查附图3-2，得；按精车加工工艺，查附图3-4，得，已知，则根据按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力，应力幅，试分别按①②，求出该截面的计算安全系数。

[解] 由题3-4可知（1）工作应力点在疲劳强度区，根据变应力的循环特性不变公式，其计算安全系数（2）工作应力点在疲劳强度区，根据变应力的平均应力不变公式，其计算安全系数第五章螺纹连接和螺旋传动5-6 已知一个托架的边板用6个螺栓及相邻的机架相连接。

托架受一及边板螺栓组的垂直对称轴线相平行、距离为250mm、大小为60kN的载荷作用。

现有如图5-50所示的两种螺栓布置形式，设采用铰制孔用螺栓连接，试问哪一种布置形式所用的螺栓直径最小？为什么？[解] 螺栓组受到剪力F和转矩，设剪力F分在各个螺栓上的力为，转矩T 分在各个螺栓上的分力为（a）中各螺栓轴线到螺栓组中心的距离为r，即r=125mm由（a）图可知，最左的螺栓受力最大（b）方案中由（b）图可知，螺栓受力最大为第八章带传动8-1 V带传动的，带及带轮的当量摩擦系数，包角，初拉力。

第三章 机械零件的强度欧阳家百（2021.03.07）习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ，取循环基数60105⨯=N ，9=m ，试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ，MPa 1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

[解] )170,0('A )0,260(C得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为：D =72mm ，d =62mm ，r =3mm 。

如用题3-2中的材料，设其强度极限σB =420MPa ，精车，弯曲，βq =1，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.14554==d D ，067.0453==d r ，查附表3-2，插值得88.1=ασ，查附图3-1得78.0≈σq ，将所查值代入公式，即查附图3-2，得75.0=σε；按精车加工工艺，查附图3-4，得91.0=σβ，已知1=q β，则根据()()()29.60,67.141,0,260,34.72,0D C A 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ，应力幅MPa20a =σ，试分别按①C r =②C σ=m ，求出该截面的计算安全系数ca S 。

[解] 由题3-4可知35.2,2.0MPa,260MPa,170s 1-====σσK Φσσ （1）C r =工作应力点在疲劳强度区，根据变应力的循环特性不变公式，其计算安全系数 （2）C σ=m工作应力点在疲劳强度区，根据变应力的平均应力不变公式，其计算安全系数第五章 螺纹连接和螺旋传动习题答案5-5 图5-49是由两块边板和一块承重板焊接的龙门起重机导轨托架。

第三章 机械零件的强度习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ，取循环基数60105⨯=N ，9=m ，试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσN MPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ，MPa 1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

[解] )170,0('A )0,260(C 012σσσΦσ-=- σΦσσ+=∴-1210 MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ 得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为：D =72mm ，d =62mm ，r =3mm 。

如用题3-2中的材料，设其强度极限σB =420MPa ，精车，弯曲，βq =1，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.14554==d D，067.0453==d r ，查附表3-2，插值得88.1=ασ，查附图3-1得78.0≈σq ，将所查值代入公式，即()()69.1188.178.0111k =-⨯+=-α+=σσσq查附图3-2，得75.0=σε；按精车加工工艺，查附图3-4，得91.0=σβ，已知1=q β，则35.211191.0175.069.1111k =⨯⎪⎭⎫ ⎝⎛-+=⎪⎪⎭⎫ ⎝⎛-+=qσσσσββεK ()()()35.267.141,67.141,0,260,35.2170,0D C A ∴ 根据()()()29.60,67.141,0,260,34.72,0D C A 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ，应力幅MPa 20a =σ，试分别按①C r =②C σ=m ，求出该截面的计算安全系数ca S 。

机械设计课后习题答案濮良贵第三章机械零件的强度p45习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-ζ，取循环基数60105?=N ，9=m ，试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111===--N N ζζN M P a 3.324105.2105180946920112===--N N ζζNM P a 0.227102.6105180956930113===--N N ζζN 3-2已知材料的力学性能为MPa 260=s ζ，MPa 1701=-ζ，2.0=ζΦ，试绘制此材料的简化的等寿命寿命曲线。

[解])170,0('A)0,260(C012ζζζΦζ-=-ζΦζζ+=∴-1210M P a 33.2832.0117021210=+?=+=∴-ζΦζζ 得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为：D =72mm ，d =62mm ，r =3mm 。

如用题3-2中的材料，设其强度极限σB =420MPa ，精车，弯曲，βq =1，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.145 54==dD ，067.0453==d r，查附表3-2，插值得88.1=αζ，查附图3-1得78.0≈ζq ，将所查值代入公式，即()()69.1188.178.0111k =-?+=-α+=ζζζq查附图3-2，得75.0=ζε；按精车加工工艺，查附图3-4，得91.0=ζβ，已知1=q β，则35.211191.0175.069.1111k = ??-+= ??-+=q ζζζζββεK ()()()35.267.141,67.141,0,260,35.2170,0D C A ∴根据()()()29.60,67.141,0,260,34.72,0D C A 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =ζ，应力幅MPa 20a =ζ，试分别按①C r =②C ζ=m ，求出该截面的计算安全系数ca S 。

第三章 机械零件的强度习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ，取循环基数60105⨯=N ，9=m ，试求循环次数N分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσN MPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ，MPa 1701=-σ，2.0=σΦ，试绘制此材料的简化的等寿命寿命曲线。

[解] )170,0('A )0,260(C 012σσσΦσ-=-Θ σΦσσ+=∴-121MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-3一圆轴轴肩处的尺寸为：D =72mm ，d =62mm ，r =3mm 。

材料为40CrNi ，设其强度极限σB =900MPa ，屈服极限750MPa s σ=试计算周健的弯曲有效应力集中系数k σ。

[解] 因1.16D d =，0.048rd=，查附表3-2，插值得 1.995σα=，查附图3-1得78.0≈σq ，将所查值代入公式，即()()k 1110.78 1.9951 1.896σσσq α=+-=+⨯-=3-4圆轴轴肩处的尺寸为：D =54mm ，d =45mm ，r =3mm 。

如用题3-2中的材料，设其强度极限σB=420MPa ，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.14554==d D ，067.0453==d r ，查附表3-2，插值得88.1=ασ，查附图3-1得78.0≈σq ，将所查值代入公式，即()()69.1188.178.0111k =-⨯+=-α+=σσσq查附图3-2，得0.7σε=；按精车加工工艺，查附图3-4，得91.0=σβ，已知1=q β，则k 11 1.691111 2.510.70.911σσσσq K εββ⎛⎫⎛⎫=+-=+-⨯= ⎪ ⎪⎝⎭⎝⎭()()()170141.670,,260,0,141.67,2.51 2.51A C D ∴根据()()()0,67.73,260,0,141.67,56.44A C D 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =σ，应力幅MPa 20a =σ，试分别按①C r =②C σ=m ，求出该截面的计算安全系数ca S 。