勾股定理_经典题型(偏难)复习过程

CA BDBAC DB专题复习：勾股定理1、勾股定理考点一、勾股定理定义：直角三角形两直角边的平方和等于斜边的平方。

解释：如果直角三角形两直角边分别为a，b，斜边为c，那么a2+b2=c2(古时候把直角三角形中较短边叫做“勾”，较长的直角边为“股”，斜边称为“弦”)典型例题例题1、（1）在直角三角形ABC中，AC=5，BC=12，求AB的长。

（2）在直角三角形ABC中，AB=25，AC=20，求BC的长。

常见的勾股数：3，4，5；5，12，13；6，8，10等技巧总结：利用勾股定理，在直角三角形中，已知两边可求第三边；一般情况下，用a，b 表示直角边，c表示斜边，则有a2+b2=c2，还可以有其他形式的变式。

例题2、一个零件的的形状如图所示，已知AC=3，AB=4，BD=12,求CD的长.例题3、如图所示，已知三角形ABC中，AB=10，BC=21，AC=17，求BC边上的高。

技巧总结：有时某些线段不可以直接写出来，可以用数学转化的思想，构造直角三角形，再求出答案，也可以用勾股定理建立方程去求。

例题4、如图，台风过后某小学的旗杆在B处断裂，旗杆顶部A落在离旗杆底部点C8米处，已知旗杆长16米，则旗杆是在距底部多少米处断裂？技巧总结：要用勾股定理的变形公式。

例题5、已知：在△ABC 中，∠C=90°，∠A 、∠B 、∠C 的对边为a 、b 、c 。

求证：a 2＋b 2=c 2。

技巧总结：分析：左右两边的正方形边长相等，则两个正方形的面积相等。

左边S=4×21ab ＋c 2，右边S=（a+b ）2，左边和右边面积相等，即4×21ab ＋c 2=（a+b ）2 对应的课堂练习：1. 下列说法正确的是（ ）A .若 a 、b 、c 是△ABC 的三边，则a 2＋b 2＝c 2B .若 a 、b 、c 是Rt △ABC 的三边，则a 2＋b 2＝c 2C .若 a 、b 、c 是Rt △ABC 的三边， 90=∠A ，则a 2＋b 2＝c 2D .若 a 、b 、c 是Rt △ABC 的三边， 90=∠C ，则a 2＋b 2＝c 22. △ABC 的三条边长分别是a 、b 、c ，则下列各式成立的是（ ） A ．c b a =+ B.c b a >+ C.c b a <+ D.222c b a =+ 3．一个直角三角形中，两直角边长分别为3和4，下列说法正确的是（ ） A ．斜边长为25 B ．三角形周长为25C ．斜边长为5D ．三角形面积为20 4．在R t A B C ∆中， 90=∠C ， （1）如果a =3，b =4，则c = ； （2）如果a =6，b =8，则c = ； （3）如果a =5，b =12，则c = ；(4) 如果a =15，b =20，则c = .5．如图,三个正方形中的两个的面积S 1＝25，S 2＝144，则另一个的面积S 3为_______1．如图，直角△ABC 的主要性质是：∠C=90°，（用几何语言表示）⑴两锐角之间的关系： ；⑵若D 为斜边中点，则斜边中线 ；⑶若∠B=30°，则∠B 的对边和斜边： ；⑷三边之间的关系： 。

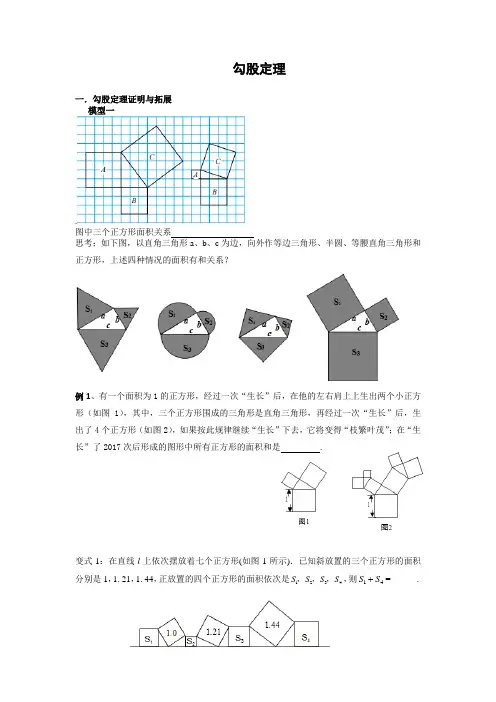
勾股定理一．勾股定理证明与拓展 模型一. 图中三个正方形面积关系思考：如下图，以直角三角形a 、b 、c 为边，向外作等边三角形、半圆、等腰直角三角形和正方形，上述四种情况的面积有和关系？例1、有一个面积为1的正方形，经过一次“生长”后，在他的左右肩上上生出两个小正方形（如图1），其中，三个正方形围成的三角形是直角三角形，再经过一次“生长”后，生出了4个正方形（如图2），如果按此规律继续“生长”下去，它将变得“枝繁叶茂”；在“生长”了2017次后形成的图形中所有正方形的面积和是 .变式1：在直线l 上依次摆放着七个正方形(如图1所示)．已知斜放置的三个正方形的面积分别是1，1. 21，1. 44，正放置的四个正方形的面积依次是1234S S S S ，，，，则41S S =______.变式2：如图，四边形ABCD中，AD∥BC，∠ABC+∠DCB=90°，且BC=2AD，以AB、BC、DC为边向外作正方形，其面积分别为S1、S2、S3，若S1=3，S3=9，求S2.（变式2）（变式3）变式3：如图，Rt△ABC 的面积为10cm2，在AB 的同侧，分别以AB，BC，AC 为直径作三个半圆，则阴影部分的面积为．（难题）如图，是小明为学校举办的数学文化节设计的标志，在△ABC 中，∠ACB＝ 90°，以△ABC 的各边为边作三个正方形，点G 落在HI 上，若AC＋BC＝6，空白部分面积为10.5，则阴影部分面积模型二外弦图DCBA内弦图GFEH例题2.四年一度的国际数学大会于2002年8月20日在北京召开，大会会标如图所示，它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形，若大正方形的面积为13，每个直角三角形两直角边的和是5。

求中间小正方形的面积为__________;变式1：如图，是用4个全等的直角三角形与1个小正方形镶嵌而成的正方图案，已知大正方形面积为25，小正方形面积为1，若用x 、y 表示直角三角形的两直角边（x y >），下列四个说法：①2225x y +=，②2x y -=，③2125xy +=，④9x y +=．其中说法正确的有___________（填序号）.(变式1) (变式2)变式2：如图,正方形ABCD 的边长为10，AG=CH=8，BG=DH=6，连接GH ，则线段GH 的长 为变式3：我国汉代数学家赵爽为了证明勾股定理，创制了一副“弦图”，后人称为“赵爽弦图”（如图5），图6是由弦图变化得到的，他是由八个全等的直角三角形拼接而成。

初中数学期末复习勾股定理重点题型分类+解析初中数学期末复习勾股定理重点题型分类+解析！_梯子_正方形_的底部题型一：利用勾股定理进行线段计算如果单独考查勾股定理，通常是给我们送分的，非常简单，我们只有熟记勾股定理的公式、常见的勾股数，以及常见的特殊rt△的三边比例，即可以轻松解出题目。

【例1】一驾2.5米长的梯子靠在一座建筑物上，梯子的底部离建筑物0.7米，如果梯子的顶部滑下0.4米，梯子的底部向外滑出多远（其中梯子从ab位置滑到cd位置）？【分析】本题是常见的梯子滑动问题，是勾股定理结合实际问题产生的题型。

英对实际问题，我们需要实际问题抽象成简单的几何图形，再利用勾股定理解答。

题目要求梯子的底部滑出多远，就要求梯子原先顶部的高度ao，且三角形aob，三角形cod均为直角三角形．可以运用勾股定理求解．解：在直角三角形aob中，根据勾股定理ab 2=ao 2+ob 2，可以求得：oa= =2.4米，现梯子的顶部滑下0.4米，即oc=2.4-0.4=2米，且cd=ab=2.5米，所以在直角三角形cod中，即do= =1.5米，所以梯子的底部向外滑出的距离为1.5米-0.7米=0.8米．答：梯子的底部向外滑出的距离为0.8米．题型二：勾股定理的证明过程勾股定理的证明过程同样是勾股定理的一个常考点。

因此我们同样要熟知勾股定的常见证明过程。

这个需要同学们查看课本，回忆整个证明过程。

下面给出常见的考题类型。

【例2】《勾股圆方图》是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形（如图（1））．设每个直角三角形中较短直角边为a，较长直角边为b，斜边为c。

（1）利用图（1）面积的不同表示方法验证勾股定理．（2）实际上还有很多代数恒等式也可用这种方法说明其正确性．试写出图（2）所表示的代数恒等式：（）；（3）如果图（1）大正方形的面积是13，小正方形的面积是1，求（a+b）2的值．【分析】（1）如图（1），根据四个全等的直角三角形的面积+阴影部分小正方形的面积=大正方形的面积，代入数值，即可证明；（2）5个矩形，长宽分别为x，y；两个边长分别为y的正方形和两个边长为x的正方形，可以看成一个长宽为x+2y，2x+y的矩形；（3）利用（1）的结论进行解答．解：（1）图（1）中的大正方形的面积可以表示为c 2，也可表示为（b-a）2+4× ab∴（b-a）2+4× ab=c 2化简得b 2-2ab+b 2+2ab=c 2∴当∠c=90°时，a 2+b 2=c 2；（2）（x+y）（x+2y）=x 2+3xy+2y 2（3）依题意得 a2+ b2＝ c2＝13 ( b− a) 2＝1 则2ab=12∴（a+b） 2=a 2+b 2+2ab=13+12=25，即（a+b） 2=25．中考数学答题要点归纳，考前看这一篇就够了！中考数学复习9种题型答题模板+易错题练习，含答案！初中数学7-9年级，21个逢考必出的知识点，初中三年都适用！初中数学7-9年级，必考应用题分类+数量关系大全！初中数学复习，整式运算的几何背景与应用，常考题型解析！。

勾股定理的题型与解题方法一、知识点1、勾股定理：直角三角形两直角边a 、b 的平方和等于斜边c 的平方。

（即：a 2+b 2=c 2） 2、勾股定理的逆定理：如果三角形的三边长：a 、b 、c 有关系a 2+b 2=c 2，那么这个三角形是直角三角形。

3、满足222c b a =+的三个正整数，称为勾股数。

二、典型题型题型1、求线段的长度例1、如图，在△ABC 中，∠ACB=90º， CD ⊥AB ，D 为垂足，AC=6cm,BC=8cm. 求① △ABC 的面积； ②斜边AB 的长；③斜边AB 上的高CD 的长。

练习1、等腰三角形的，腰长为25，底边长14，则底边上的高是________，面积是_________。

2、一个直角三角形的三边长为连续偶数，则它的各边长为________。

3、一根旗杆在离地9米处断裂，旗杆顶部落在离旗杆底部12米处，旗杆折断之前有多高为_________。

4、直角三角形两直角边分别为5厘米、12厘米，那么斜边上的高是（ ）A 、6厘米；B 、 8厘米；C 、 80/13厘米；D 、 60/13厘米；5、直角三角形中两条直角边之比为3：4，且斜边为20cm ，求（1）两直角边的长（2）斜边上的高线长题型2、判断直角三角形例2、如图己知13,12,4,3,====⊥AD CD BC AB BC AB 求四边形ABCD 的面积DABC1．下列各组线段中，能构成直角三角形的是（ ）A ．2，3，4B ．3，4，6C ．5，12，13D ．4，6，72. 三角形的三边为a 、b 、c ，由下列条件不能判断它是直角三角形的是（ ）A ．a :b :c=8∶16∶17B ． a 2-b 2=c 2C ．a 2=(b+c)(b-c) D ． a :b :c =13∶5∶12 3. 三角形的三边长为ab c b a 2)(22+=+,则这个三角形是( )A . 等边三角形B . 钝角三角形C . 直角三角形D . 锐角三角形.4、已知：如图，四边形ABCD 中，AB=20，BC=15，CD=7，AD=24，∠B=90°，求证：∠A+∠C=180°。

勾股定理复习一．知识归纳 １．勾股定理内容：直角三角形两直角边的平方和等于斜边的平方；表示方法：如果直角三角形的两直角边分别为a ，b ，斜边为c ，那么222a b c += ２.勾股定理的证明勾股定理的证明方法很多，常见的是拼图的方法 用拼图的方法验证勾股定理的思路是①图形通过割补拼接后，只要没有重叠，没有空隙，面积不会改变②根据同一种图形的面积不同的表示方法，列出等式，推导出勾股定理 常见方法如下：方法一：4EFGH S S S ∆+=正方形正方形ABCD，2214()2ab b a c ⨯+-=，化简可证． cbaHG F EDCB A方法二：bacbac cabcab四个直角三角形的面积与小正方形面积的和等于大正方形的面积．四个直角三角形的面积与小正方形面积的和为221422S ab c ab c =⨯+=+大正方形面积为222()2S a b a ab b =+=++ 所以222a b c += 方法三：1()()2S a b a b =+⋅+梯形，2112S 222ADE ABE S S ab c ∆∆=+=⋅+梯形，化简得证a bcc baE D CBA３.勾股定理的适用范围勾股定理揭示了直角三角形三条边之间所存在的数量关系，它只适用于直角三角形 ４.勾股定理的应用①已知直角三角形的任意两边长，求第三边在ABC ∆中，90C ∠=︒，则c，b =，a =②知道直角三角形一边，可得另外两边之间的数量关系 ③可运用勾股定理解决一些实际问题 ５.勾股定理的逆定理如果三角形三边长a ，b ，c 满足222a b c +=，那么这个三角形是直角三角形，其中c 为斜边①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法，它通过“数转化为形”来确定三角形的可能形状，在运用这一定理时，可用两小边的平方和22a b +与较长边的平方2c 作比较，若它们相等时，以a ，b ，c 为三边的三角形是直角三角形；若222a b c +<，时，以a ，b ，c 为三边的三角形是钝角三角形；若222a b c +>，时，以a ，b ，c 为三边的三角形是锐角三角形；②定理中a ，b ，c 及222a b c +=只是一种表现形式，不可认为是唯一的，如若三角形三边长a ，b ，c 满足222a c b +=，那么以a ，b ，c 为三边的三角形是直角三角形，但是b 为斜边③勾股定理的逆定理在用问题描述时，不能说成：当斜边的平方等于两条直角边的平方和时，这个三角形是直角三角形６.勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数，即222a b c +=中，a ，b ，c 为正整数时，称a ，b ，c 为一组勾股数②记住常见的勾股数可以提高解题速度，如3,4,5；6,8,10；5,12,13；7,24,25等③用含字母的代数式表示n 组勾股数： 221,2,1n n n -+（2,n ≥n 为正整数）； 2221,22,221n n n n n ++++（n 为正整数） 22222mn m n m n -+，，（,m n >m ，n 为正整数）７．勾股定理的应用勾股定理能够帮助我们解决直角三角形中的边长的计算或直角三角形中线段之间的关系的证明问题．在使用勾股定理时，必须把握直角三角形的前提条件，了解直角三角形中，斜边和直角边各是什么，以便运用勾股定理进行计算，应设法添加辅助线（通常作垂线），构造直角三角形，以便正确使用勾股定理进行求解． ８.．勾股定理逆定理的应用勾股定理的逆定理能帮助我们通过三角形三边之间的数量关系判断一个三角形是否是直角三角形，在具体推算过程中，应用两短边的平方和与最长边的平方进行比较，切不可不加思考的用两边的平方和与第三边的平方比较而得到错误的结论．９.勾股定理及其逆定理的应用勾股定理及其逆定理在解决一些实际问题或具体的几何问题中，是密不可分的一个整体．通常既要通过逆定理判定一个三角形是直角三角形，又要用勾股定理求出边的长度，二者相辅相成，完成对问题的解决． 常见图形：ABC30°D CBA ADB CCDA题型一：直接考查勾股定理 例1. 在ABC ∆中，90C ∠=︒．⑴已知6AC =，8BC =．求AB 的长 ⑵已知17AB =，15AC =，求BC 的长题型二：应用勾股定理建立方程 例2.⑴在ABC ∆中，90ACB ∠=︒，5AB =cm ，3BC =cm ，CD AB ⊥于D ，CD ＝⑵已知直角三角形的两直角边长之比为3:4，斜边长为15，则这个三角形的面积为⑶已知直角三角形的周长为30cm ，斜边长为13cm ，则这个三角形的面积为例3. 如图ABC ∆中，90C ∠=︒，12∠=∠， 1.5CD =，2.5BD =，求AC 的长21EDCBA例4. 如图Rt ABC ∆，90C ∠=︒3,4AC BC ==,分别以各边为直径作半圆，求阴影部分面积题型三：实际问题中应用勾股定理例5. 如图有两棵树，一棵高8cm ，另一棵高2cm ，两树相距8cm ，一只小鸟从一棵树的树梢飞到另一棵数的树梢，至少飞了 mABCD E题型四：应用勾股定理逆定理，判定一个三角形是否是直角三角形例6. 已知三角形的三边长为a ，b ，c ，判定ABC ∆是否为Rt ∆① 1.5a =，2b =， 2.5c = ②54a =，1b =，23c =例7. 三边长为a ，b ，c 满足10a b +=，18ab =，8c =的三角形是什么形状？题型五：勾股定理与勾股定理的逆定理综合应用例8. 已知ABC ∆中，13AB =cm ，10BC =cm ，BC 边上的中线12AD =cm ，求证：AB AC =例题9 如图3，正方形ABCD 中，E 是BC 边上的中点，F 是AB 上一点，且AB FB 41=那么△DEF 是直角三角形吗？为什么？题型六：关于翻折问题例10.如图，矩形纸片ABCD的边AB=10cm，BC=6cm，E 为BC上一点，将矩形纸片沿AE折叠，点B恰好落在CD边上的点G处，求BE的长.变式：如图，AD是△ABC的中线，∠ADC=45°，把△ADC 沿直线AD翻折，点C落在点C’的位置，BD=4,求BC’的长.题型七：旋转问题：例11．△ABC是直角三角形，BC是斜边，将△ABP绕点A逆时针旋转后，能与△AC P′重合，若AP=3，求PP′的长。

勾股定理知识点回顾（一）勾股定理１．定理：直角三角形两条直角边ａ、ｂ的平方和等于斜边ｃ的平方：ａ２＋ｂ２＝ｃ２２．逆定理：如果三角形的三边长ａ、ｂ、ｃ有下面关系：ａ２＋ｂ２＝ｃ２，那么这个三角形是直角三角形．３．勾股数：能构成为直角三角形三条边长的三个正整数，称为勾股数．（二）直角三角形１．定义：有一个角是直角的三角形叫直角三角形．２．性质：（１）直角三角形的两个锐角互余．（２）直角三角形中，如果一个锐角等于３０°，那么它所对的直角边等于斜边的一半．（３）在直角三角形中，如果一条直角边等于斜边的一半，那么这条直角边所对的角等于３０°．（４）直角三角形斜边上的中线等于斜边的一半．（５）勾股定理．３．判定：（１）定义：有一个角是直角的三角形是直角三角形（２）一个三角形，若有两个角互余，那么这个三角形是直角三角形．（３）如果一个三角形中的一条边上的中线等于这条边的一半，那么这个三角形是直角三角形．（４）勾股定理的逆定理一、专题讲解【例１】如图，△ＡＢＣ中，ＡＢ＝１３，ＢＣ＝１４，ＡＣ＝１５，求ＢＣ边上的高ＡＤ．解设ＢＤ＝ｘ，则ＤＣ＝１４－ｘ在Ｒｔ△ＡＢＤ中，由勾股定理得ＡＤ２＋ｘ２＝１３２∴ＡＤ２＝１３２－ｘ２同理：在Ｒｔ△ＡＤＣ中，ＡＤ２＝１５２－（１４－ｘ）２∴１３２－ｘ２＝１５２－（１４－ｘ）２，解方程得ｘ＝５在Rt△ABD中，由勾股定理得AD = 132 - 52 = 12．说明高ＡＤ虽然是两个直角三角形的边，但哪个直角三角形的边都有未知数，要想求这未知数，必须利用两直角三角形的公共边ＡＤ列出方程，才能求得结果．这在几何的计算问题中是经常应用的．2、在矩形纸片ABCD中，AD=4cm，AB=10cm，按如图方式折叠，使点B与点D重合，折痕为EF．求DE 的长；解：（1）由翻折不变性可知，EB=ED，设DE为xcm，则EB=xcm，∵AB=10cm，∴AE=AB-x=10-x，又∵AD=4cm，∴在Rt△ADE中，AD2+AE2=DE2，即42+（10-x）2=x2，化简得：16+100+x2-20x=x2，解得：x=5.8，即DE=5.8；【例4】如图，在矩形ABCD中，AB＝6，BC＝8。

勾股定理解题步骤勾股定理是初中数学中的一道经典题目，也是我们日常生活中经常用到的数学知识。

勾股定理的应用范围非常广泛，包括计算三角形的各种属性，如边长、角度、面积等等。

在这里，我将为大家介绍勾股定理解题的步骤。

步骤一：了解勾股定理的定义和公式勾股定理是指直角三角形的两条直角边的平方和等于斜边的平方，即a² + b² = c²。

其中，a和b分别表示直角三角形的两条直角边，c表示斜边。

步骤二：确定已知条件和未知量在解题之前，我们需要先确定已知条件和未知量。

已知条件是指我们已经知道的数值或者信息，未知量是指我们需要求解的数值或者信息。

在勾股定理中，已知条件通常是两条直角边的长度，未知量通常是斜边的长度。

步骤三：应用勾股定理求解未知量在确定已知条件和未知量之后，我们就可以应用勾股定理求解未知量了。

具体步骤如下：1. 将已知条件代入勾股定理公式中，得到一个方程式。

2. 对该方程式进行变形，将未知量单独提出来。

3. 对该方程式进行求解，得到未知量的值。

步骤四：检验答案在求解出未知量的值之后，我们需要对答案进行检验。

检验的方法是将已知条件代入勾股定理公式中，看是否符合等式左右两边相等的要求。

如果符合要求，则说明我们求解出来的答案是正确的；如果不符合要求，则说明我们的求解过程出现了错误，需要重新检查。

总结：以上就是勾股定理解题的步骤。

当然，在实际应用中，我们还需要根据具体情况进行适当的变形和推导。

但无论如何，掌握好勾股定理的基本原理和解题方法，能够帮助我们更好地应用数学知识解决实际问题。

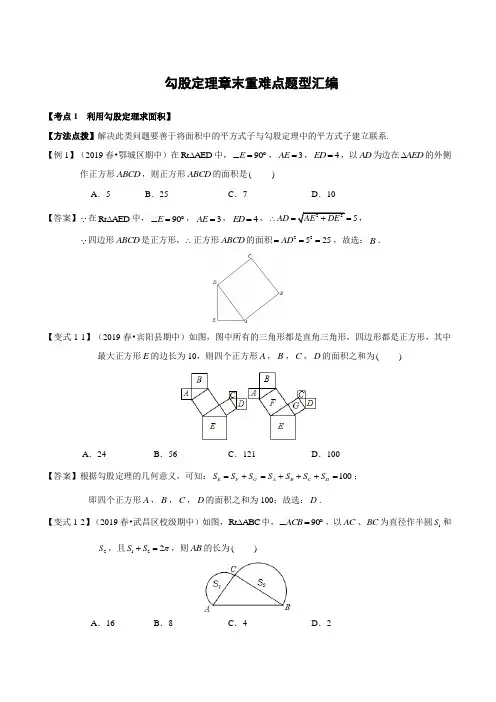
勾股定理章末重难点题型汇编【考点1 利用勾股定理求面积】【方法点拨】解决此类问题要善于将面积中的平方式子与勾股定理中的平方式子建立联系.【例1】（2019春•鄂城区期中）在Rt AED ∆中，90E ∠=︒，3AE =，4ED =，以AD 为边在AED ∆的外侧作正方形ABCD ，则正方形ABCD 的面积是( )A ．5B ．25C ．7D ．10 【答案】在Rt AED ∆中，90E ∠=︒，3AE =，4ED =，225AD AE DE ∴=+=，四边形ABCD 是正方形，∴正方形ABCD 的面积22525AD ===，故选：B ．【变式1-1】（2019春•宾阳县期中）如图，图中所有的三角形都是直角三角形，四边形都是正方形，其中最大正方形E 的边长为10，则四个正方形A ，B ，C ，D 的面积之和为( )A ．24B ．56C ．121D ．100【答案】根据勾股定理的几何意义，可知：E F G S S S =+A B C D S S S S =+++100=；即四个正方形A ，B ，C ，D 的面积之和为100；故选：D ．【变式1-2】（2019春•武昌区校级期中）如图，Rt ABC ∆中，90ACB ∠=︒，以AC 、BC 为直径作半圆1S 和2S ，且122S S π+=，则AB 的长为( )A ．16B ．8C ．4D ．2【分析】根据勾股定理得到222AC BC AB +=，根据圆的面积公式计算，得到答案．【答案】解：由勾股定理得，222AC BC AB +=， 2222111()()()222228AC BC AC BC ππππ⨯+⨯=⨯+=， 解得，2216AC BC +=，则22216AB AC BC =+=，解得，4AB =，故选：C ．【点睛】本题考查勾股定理，如果直角三角形的两条直角边长分别是a ，b ，斜边长为c ，那么222a b c +=．【变式1-3】（2019春•兰山区期中）如图，其中所有三角形都是直角三角形，所有四边形都是正方形．若1S ，2S ，3S ，4S 和S 分别代表相应的正方形的面积，且14S =，29S =，38S =，410S =，则S 等于( )A ．25B ．31C ．32D ．40【答案】如图，由题意得：21213AB S S =+=，23418AC S S =+=，22231BC AB AC ∴=+=，231S BC ∴==．故选：B ．【考点2 判断直角三角形】【方法点拨】如果三角形两边的平方和等于第三边的平方，那么这个三角形是直角三角形.【例2】（2019春•芜湖期中）在以线段a ，b ，c 的长三边的三角形中，不能构成直角三角形的是( )A ．4a =，5b =，6c =B ．::5:12:13a b c =C ．2a =3b =，5c =D ．4a =，5b =，3c = 【答案】A 、222456+≠，不能构成直角三角形，故本选项符合题意；B 、设三角形三边为5k ，12k ，13k ，2(5)(k +2212)(13)k k =，能构成直角三角形，故本选项不符 合题意；C 、(22)(+23)(=25)，能构成直角三角形，故本选项不符合题意；D 、222345+=，能构成直角三角形，故本选项不符合题意；故选：A ．【变式2-1】（2018春•淮南期中）a 、b 、c 为ABC ∆三边，不是直角三角形的是( )A ．::3:4:5ABC ∠∠∠=B ．54a =，1b =，34c =C ．222a c b =-D ．8a k =，17b k =，15c k =【答案】A 、::3:4:5A B C ∠∠∠=，∴设3A x ∠=，则4B x ∠=，5C x ∠=，180A B C ∠+∠+∠=︒，即345180x x x ++=︒，解得，15x =︒，55157590x ∴=⨯︒=︒<︒，故本选项错误；B 、2226810+=，222a b c ∴+=，故本选项正确；C 、222a b c =-，222a c b ∴+=，故本选项正确；D 、22281517k k k +=，222a b c ∴+=，故本选项正确．故选：A ．【变式2-2】（2018秋•金牛区校级期中）下列说法中，正确的有( )①如果0A B C ∠+∠-∠=，那么ABC ∆是直角三角形；②如果::5:12:13A B C ∠∠∠=，则ABC ∆是直角三角形；③如果三角形三边之比为7:10:17，则ABC ∆为直角三角形；④如果三角形三边长分别是24n -、4n 、24(2)n n +>，则ABC ∆是直角三角形；A ．1个B ．2个C ．3个D ．4个【答案】解：①正确，由三角形内角和定理可求出C ∠为90度；②不正确，因为根据三角形的内角和得不到90︒的角；③正确，设三边分别为7x ，10x ，17x ，则有2271017x +=；④正确，因为222(4)(4)(4)n n n -+=+．所以正确的有三个．故选：C ．【变式2-3】（2019春•寿光市期中）如图：在一个边长为1的小正方形组成的方格稿纸上，有A 、B 、C 、D 、E 、F 、七个点，则在下列任选三个点的方案中可以构成直角三角形的是( )A ．点A 、点B 、点C B ．点A 、点D 、点G C ．点B 、点E 、点FD ．点B 、点G 、点E选：C ．【考点3 利用勾股定理求最短路径】【方法点拨】解决此类问题需先将立体图形进行展开，在平面上利用两点之间线段最短作图，利用勾股定理即可求解.【例3】（2018秋•福田区校级期中）如图，一圆柱高BC 为20cm ，底面周长是10cm ，一只蚂蚁从点A 爬到点P 处吃食，且35PC BC =，则最短路线长为( )A ．20cmB ．13cmC ．14cmD ．18cm【答案】如图展开，连接AP ，则AP 就是蚂蚁爬行的最短路线长， 则90C ∠=︒，11052AC cm cm =⨯=，20BC cm =，35PC BC =，12CP cm ∴=， 勾股得：222251213()AP AC CP cm =+=+=，即蚂蚁爬行的最短路线长是13cm ，故选：B ．【变式3-1】（2018秋•沙坪坝区校级月考）如图，三级台阶，每一级的长、宽、高分别为8dm 、3dm 、2dm ．A和B 是这个台阶上两个相对的端点，点A 处有一只蚂蚁，想到点B 处去吃可口的食物，则蚂蚁沿着台阶面爬行到点B 的最短路程为( )A ．15 dmB ．17 dmC ．20 dmD ．25 dm【答案】三级台阶平面展开图为长方形，长为8dm ，宽为(23)3dm +⨯，则蚂蚁沿台阶面爬行到B 点最短路程是此长方形的对角线长．可设蚂蚁沿台阶面爬行到B 点最短路程为xdm ，由勾股定理得：22228[(23)3]17x =++⨯=，解得17x =．故选：B ．【变式3-2】（2018春•凉州区期末）如图，长方体的底面边长为1cm 和3cm ，高为6cm ．如果用一根细线从点A 开始经过4个侧面缠绕一圈到达B ，那么所用细线最短需要( )A ．12cmB ．11cmC ．10cmD ．9cm【答案】将长方体展开，连接A 、B '，则13138()AA cm '=+++=，6A B cm ''=， 根据两点之间线段最短，228610AB cm '=+=．故选：C ．【变式3-3】（2019秋•松滋市期末）如图，桌上有一个圆柱形玻璃杯（无盖）高6厘米，底面周长16厘米，在杯口内壁离杯口1.5厘米的A 处有一滴蜜糖，在玻璃杯的外壁，A 的相对方向有一小虫P ，小虫离杯底的垂直距离为1.5厘米，小虫爬到蜜糖A 处的最短距离是( )A 73B ．10厘米C ．82D ．8厘米【答案】解：如图所示：最短路径为：P A '→，将圆柱展开，2222(162)(6 1.5 1.5)10PA PE EA cm ''+÷+-+，最短路程为10PA cm '=．故选：B ．【考点4 勾股数相关问题】【方法点拨】勾股数的求法：（1）如果a 为1个大于1的奇数，b ，c 是两个连续的自然数，且有a ²=b+c ，则a,b,c 为一组勾股数；（2）如果a,b,c 为一组勾股数，那么na ，nb ，nc 也是一组勾股数，其中n 为自然数.【例4】（2018秋•新密市校级期中）下列各组数据是勾股数的有 组．（填写数量即可）（1）6，8，10 （2）1.5，2，2.5 （3）23，24，25（4）7，24，25 （5345【分析】根据勾股数：满足222a b c += 的三个正整数，称为勾股数进行计算可得答案．【答案】解：因为2226810+=；22272425+=，6，8，10，7，24，25都是正整数∴勾股数有2组，故答案为2．【变式4-1】（2019春•闽侯县期中）勾股定理222a b c +=本身就是一个关于a ，b ，c 的方程，显然这个方程有无数解，满足该方程的正整数(a ，b ，)c 通常叫做勾股数．如果三角形最长边2221c n n =++，其中一短边21a n =+，另一短边为b ，如果a ，b ，c 是勾股数，则b = （用含n 的代数式表示，其中n 为正整数）【答案】2221c n n =++，21a n =+222b n n ∴=+故答案为：222n n +【变式4-2】（2018春•襄城区期中）观察下列各组勾股数，并寻找规律：①4，3，5； ②6，8，10； ③8，15，17； ④10，24，26⋯⋯请根据你发现的规律写出第⑦组勾股数： ．【答案】观察前4组数据的规律可知：第一个数是2(1)n +；第二个是：(2)n n +；第三个数是：2(1)1n ++．所以第⑦组勾股数：16，63，65．故答案为：16，63，65【考点5 利用勾股定理求长度】【例5】（2018春•港南区期中）如图，在ABC ∆中，90ACB ∠=︒，CD AB ⊥于点D ，3AC cm =，4BC cm =，求AD ，CD 的长．【答案】90ACB ∠=︒，3AC cm =，4BC cm =，5AB cm ∴=．根据直角三角形的面积公式，得 2.4AC BC CD cm AB==． 在Rt ACD ∆中，22 1.8AD AC CD cm =-=．【变式5-1】（2018秋•滨湖区期中）在等腰ABC ∆中，已知AB AC =，BD AC ⊥于D ．（1）若48A ∠=︒，求CBD ∠的度数；（2）若15BC =，12BD =，求AB 的长．【答案】解：（1）在等腰ABC ∆中，AB AC =，BD AC ⊥，ABC C ∴∠=∠，90ADB ∠=︒，48A ∠=︒，66ABC C ∴∠=∠=︒，42ABD ∠=︒，24CBD ∴∠=︒；（2）BD AC ⊥，90BDC ∴∠=︒，15BC =，12BD =，9CD ∴=，设AB x =，则9AD x =-，90ADB ∠=︒，12BD =，22212(9)x x ∴+-=，解得，22518x =，即22518AB =． 【变式5-2】（2018春•兴义市期中）如图，在ABD ∆中，90D ∠=︒，C 是BD 上一点，已知9BC =，17AB =，10AC =，求AD 的长．【答案】解：设CD x =，则9BD BC CD x =+=+．在ACD ∆中，90D ∠=︒，222AD AC CD ∴=-，在ABD ∆中，90D ∠=︒，222AD AB BD ∴=-，2222AC CD AB BD ∴-=-，即22221017(9)x x -=-+，解得6x =，22210664AD ∴=-=，8AD ∴=．故AD 的长为8．【变式5-3】（2018秋•东明县期中）如图，在Rt ABC ∆中，90ABC ∠=︒，16AB cm =，正方形BCEF 的面积为2144cm ，BD AC ⊥于点D ，求BD 的长．【答案】正方形BCEF 的面积为2144cm ，14412BC cm ∴==，90ABC ∠=︒，16AB cm =，∴2220AC AB AC cm =+=．BD AC ⊥，∴1122ABC S AB BC BD AC ∆==，∴485BD cm =． 【考点6 勾股定理的证明】【方法点拨】勾股定理又称为毕达哥拉斯定理，通常利用面积来证明.【例6】（2019春•洛阳期中）下列两图均由四个全等的直角三角形拼接而成，且它们的两条直角边分别为a ，b ，斜边为c ，a b >．请选择一个你喜欢的图形，利用等面积法验证勾股定理．你选择的是 图，写出你的验证过程．【答案】选择的是图2，证明：2S c =大正方形，2144()2S S S ab b a =+=⨯+-大正方形小正方形，2214()2c ab b a ∴=⨯+-，整理，得22222ab b ab a c +-+=，222c a b ∴=+．故答案为：2， 【变式6-1】（2018秋•兴化市期中）我们刚刚学习的勾股定理是一个基本的平面几何定理，也是数学中最重要的定理之一．勾股定理其实有很多种证明方法．下图是1876年美国总统伽菲尔德()Garfield 证明勾股定理所用的图形：以a 、b 为直角边，以c 为斜边作两个全等的直角三角形，把这两个直角三角形拼成如图所示梯形形状，使C 、B 、D 三点在一条直线上．（1）求证：90ABE ∠=︒；（2）请你利用这个图形证明勾股定理（即证明：222)a b c +=．【答案】解：（1）Rt ACB Rt BDE ∆≅∆，CAB DBE ∴∠=∠．90CAB ABC ∠+∠=︒，90ABC DBE ∴∠+∠=︒，1809090o o ABE ∴∠=︒-=．（2）由（1）知ABE ∆是一个等腰直角三角形，212ABE S c ∆∴=． 又21()2ACDE S a b =+梯形，212ABC BDE ABE ACDE S S S S ab c ∆∆∆=++=+梯形， ∴2211()22a b ab c +=+，即222a b c +=． 【变式6-2】（2018秋•东台市期中）如图，将Rt ABC ∆绕其锐角顶点A 旋转90︒得到Rt ADE ∆，连接BE ，延长DE 、BC 相交于点F ，则有90BFE ∠=︒，且四边形ACFD 是一个正方形．（1）判断ABE ∆的形状，并证明你的结论；（2）用含b 代数式表示四边形ABFE 的面积；（3）求证：222a b c +=．【答案】（1）ABE ∆是等腰直角三角形，证明：Rt ABC ∆绕其锐角顶点A 旋转90︒得到在Rt ADE ∆，BAC DAE ∴∠=∠，90BAE BAC CAE CAE DAE ∴∠=∠+∠=∠+∠=︒，又AB AE =，ABE ∴∆是等腰直角三角形；（2）四边形ABFE 的面积等于正方形ACFD 面积，∴四边形ABFE 的面积等于：2b ．（3）BAE BFE ACFD S S S ∆∆=+正方形即：1122()()22b c b a b a =++-，整理：222()()b c b a b a =++- 222a b c ∴+=．【变式6-3】（2019春•东光县期中）ADE ∆和ACB ∆是两直角边为a ，b ，斜边为c 的全等的直角三角形，按如图所示摆放，其中90DAB ∠=︒，求证：222a b c +=．【答案】证明：连结DB ，过点D 作BC 边上的高DF ，则DF EC b a ==-．21122ACD ABC ADCB S S S b ab ∆∆=+=+四边形．又()21122ADB DCB ADCB S S S c a b a ∆∆=+=+-四边形 ∴221111()2222b abc a b a +=+-222a b c ∴+=【考点7 勾股定理逆定理的应用】【方法点拨】如果三角形两边的平方和等于第三边的平方，那么这个三角形是直角三角形.【例7】（2018春•宾阳县期中）如图，已知在四边形ABCD 中，20AB cm =，15BC cm =，7CD cm =，24AD cm =，90ABC ∠=︒．（1）连结AC ，求AC 的长；（2）求ADC ∠的度数；（3）求出四边形ABCD 的面积【分析】（1）连接AC ，利用勾股定理解答即可；（2）利用勾股定理的逆定理解答即可；（3）根据三角形的面积公式解答即可．【答案】解：（1）连接AC ，在Rt ABC ∆中，90ABC ∠=︒，20AB cm =，15BC cm =∴由勾股定理可得：2222201525AC AB BC cm =+=+=；（2）在ADC ∆中，7CD cm =，24AD cm =222CD AD AC ∴+=90ADC ∴∠=︒；（3）由（2）知，90ADC ∠=︒，∴四边形ABCD 的面积2112015724234()22ABC ACD S S cm ∆∆=+=⨯⨯+⨯⨯=， 【变式7-1】（2019春•长白县期中）如图，在四边形ABCD 中，已知12AB =，9BC =，90ABC ∠=︒，且39CD =，36DA =．求四边形ABCD 的面积．【答案】连接AC ，90ABC ∠=︒，12AB =，9BC =15AC ∴=，39CD =，36DA =222215361521AC DA +=+=，22391521CD ==， ADC ∴∆为直角三角形ACD ABC ABCD S S S ∆∆∴=-四边形1122AC AD AB BC =⨯-⨯216=． 故四边形ABCD 的面积为216．【变式7-2】（2018春•丰台区期中）如图，在四边形ABCD 中，90ABC ∠=︒，3AB =，4BC =，12DC =，13AD =，求四边形ABCD 的面积．【答案】连接AC ，90ABC ∠=︒，3AB =，4BC =，2222345AC AB BC ∴=+=+，12DC =，13AD =，222251225144169AC DC ∴+=+=+=，2213169AD ==，222AC DC AD ∴+=ACD ∴∆是90ACD ∠=︒的直角三角形，四边形ABCD 的面积ABC =∆的面积ACD +∆的面积，1122AB BC AC CD =+36=． 【变式8-3】（2019春•鄂城区期中）如图，四边形ABCD 中，4AB BC CD AD ====，90DAB B C D ∠=∠=∠=∠=︒，E 、F 分别是BC 和CD 边上的点，且14CE BC =，F 为CD 的中点，问AEF ∆是什么三角形？请说明理由．【答案】4AB BC CD AD ====，4AB =，14CE BC =1EC ∴=，3BE =， F 为CD 的中点，2DF FC ∴==，90DAB B C D ∠=∠=∠=∠=︒，22215EF ∴=+=224220AF =+=224325AE =+=． 222AE EF AF ∴=+AEF ∴∆是直角三角形．【考点9 勾股定理的实际应用】【方法点拨】将实际问题转化为直角三角形，利用勾股定理求解即可.【例9】（2019春•东湖区校级期末）数学综合实验课上，同学们在测量学校旗杆的高度时发现：将旗杆顶端升旗用的绳子垂到地面还多2米；当把绳子的下端拉开8米后，下端刚好接触地面，如图，根据以上数据，同学们准确求出了旗杆的高度，你知道他们是如何计算出来的吗？【答案】解：设旗杆高xm ，则绳子长为(2)x m +，旗杆垂直于地面，∴旗杆，绳子与地面构成直角三角形，由题意列式为2228(2)x x +=+，解得15x m =，∴旗杆的高度为15米．【变式9-1】（2019春•内黄县期末）如图，在离水面高度为8米的岸上，有人用绳子拉船靠岸，开始时绳子BC 的长为17米，此人以1米每秒的速度收绳，7秒后船移动到点D 的位置，问船向岸边移动了多少米？（假设绳子是直的，结果保留根号）【分析】在Rt ABC ∆中，利用勾股定理计算出AB 长，再根据题意可得CD 长，然后再次利用勾股定理计算出AD 长，再利用BD AB AD =-可得BD 长．【答案】解：在Rt ABC ∆中90CAB ∠=︒，17BC =米，8AC =米， 2215AB BC AC ∴=-=（米)此人以1米每秒的速度收绳，7秒后船移动到点D 的位置，171710CD ∴=-⨯=（米)22100646AD CD AC ∴=-=-=（米)，1569BD AB AD ∴=-=-=（米)，答：船向岸边移动了9米．【变式9-2】（2019春•道里区期末）某地区为了开发农业，决定在公路上相距25km 的A 、B 两站之间E 点修建一个土特产加工基地，使E 点到C 、D 两村的距离相等，如图，DA AB ⊥于点A ，CB AB⊥于点B ，15DA km =，10CB km =，求土特产加工基地E 应建在距离A 站多少km 的地方？【答案】设AE x =千米，则(25)BE x =-千米， 在Rt DAE ∆中，222DA AE DE +=，在Rt EBC ∆中，222BE BC CE +=，CE DE =，2222DA AE BE BC ∴+=+，22221510(25)x x ∴+=+-，解得，10x =千米．答：基地应建在离A 站10千米的地方．【考点10 利用勾股定理解折叠问题】【例10】（2019春•番禺区期末）如图，有一块直角三角形纸片，两直角边6AC cm =，8BC cm =，将纸片沿AD 折叠，直角边AC 恰好落在斜边上，且与AE 重合，求BDE ∆的面积．【答案】 6AC cm =， 2210AB AC CB cm ∴=+将纸片沿AD 折叠，直角边AC 恰好落在斜边上，且与AE 重合，6AC AE cm ∴==，90DEB ∠=︒1064BE cm ∴=-=设CD DE x ==，则在Rt DEB ∆中，2224(8)x x +=-解得3x =，即DE 等于3cmBDE ∴∆的面积14362=⨯⨯=答：BDE ∆的面积为26cm【变式10-1】（2018秋•建邺区期末）如图，把长为12cm 的纸条ABCD 沿EF ，GH 同时折叠，B 、C 两点恰好落在AD 边的P 点处，且90FPH ∠=︒，3BF cm =，求FH 的长．【答案】由翻折不变性可知：BF PF =，CH PH =，设FH x cm =，则(9)PH x cm =-，在Rt PFH ∆中，90FPH ∠=︒，222FH PH PF ∴=+，222(9)3x x ∴=-+，5x ∴=，FH ∴的长是5cm ．【变式10-2】（2019秋•杭州期中）如图，把长方形ABCD 沿AC 折叠，AD 落在AD '处，AD '交BC 于点E ，已知2AB cm =，4BC cm =．（长方形的对边相等，四个角都为直角）（1）求证：AE EC =；（2）求EC 的长；（3）求重叠部分的面积．【答案】解：（1）四边形ABCD 是矩形，AB CD ∴=，AD BC =，90B ∠=︒，//AD BC DAC BCA ∴∠=∠．ADC ∆与△AD C '关于AC 成轴对称ADC ∴∆≅△AD C '，DAC D AC ∴∠=∠'，D AC ACB ∴∠'=∠，AE EC ∴=；（2）2AB cm =，4BC cm =，2CD cm ∴=，4AD cm =．设EC x =，就有AE x =，4BE x =-，在Rt ABE ∆中，由勾股定理，得224(4)x x +-=，解得： 2.5x =．答：EC 的长为2.5cm ；（3）2AEC EC AB S ∆=，22.52 2.52AEC S cm ∆⨯==． 答：重叠部分的面积为22.5cm ．【变式10-3】（2018春•杜尔伯特县期中）如图，将边长为8cm 的正方形ABCD 折叠，使点D 落在BC 边的中点E 处，点A 落在F 处，折痕为MN ．（1）求线段CN 长．（2）连接FN ，并求FN 的长．【答案】解：（1）设NC x =，则8DN x =-．由翻折的性质可知：8EN DN x ==-．在Rt ENC ∆中，由勾股定理可知：222EN EC NC =+，222(8)4x x -=+，解得：3x =，即3NC cm =．（2）如图所示，连接AN ．在Rt 三角形ADN 中，22228589AN AD ND =++ 由翻折的性质可知89FN AN ==。

勾股定理（知识归纳+题型突破）1.了解勾股定理的历史，掌握勾股定理的证明方法；2.理解并掌握勾股定理及逆定理的内容；3.能应用勾股定理及逆定理解决有关的实际问题.一、勾股定理1.勾股定理：直角三角形两直角边a b 、的平方和等于斜边c 的平方.（即：222a b c +=）二、勾股定理的逆定理1.勾股定理的逆定理如果三角形的三边长a b c 、、，满足222a b c +=，那么这个三角形是直角三角形.要点：应用勾股定理的逆定理判定一个三角形是不是直角三角形的基本步骤：（1）首先确定最大边，不妨设最大边长为c ；（2）验证：22a b +与2c 是否具有相等关系：若222a b c +=，则△ABC 是以∠C 为90°的直角三角形；若222a b c +＞时，△ABC 若222a b c +＜时，△ABC 是钝角三角形．2.勾股数满足不定方程222x y z +=的三个正整数，称为勾股数（又称为高数或毕达哥拉斯数），显然，以x y z 、、为三边长的三角形一定是直角三角形.要点：常见的勾股数：①3、4、5；②5、12、13；③8、15、17；④7、24、25；⑤9、40、41.如果(a b c 、、)是勾股数，当t 为正整数时，以at bt ct 、、为三角形的三边长，此三角形必为直角三角形.观察上面的①、②、④、⑤四组勾股数，它们具有以下特征：1.较小的直角边为连续奇数；2.较长的直角边与对应斜边相差1.3.假设三个数分别为a b c 、、，且a b c <<，那么存在2a b c =+成立.（例如④中存在27＝24＋25、29＝40＋41等）三、勾股定理与勾股定理逆定理的区别与联系区别：勾股定理是直角三角形的性质定理，而其逆定理是判定定理；联系：勾股定理与其逆定理的题设和结论正好相反，两者互为逆定理，都与直角三角形有关.四、勾股定理的应用勾股定理反映了直角三角形三边之间的关系，是直角三角形的重要性质之一，其主要应用是：（1）已知直角三角形的两边，求第三边；（2）利用勾股定理可以证明有关线段平方关系的问题；（3）解决与勾股定理有关的面积计算；（4）勾股定理在实际生活中的应用．A．8【答案】A【分析】利用勾股定理进行求解即可．∠=【解析】解：∵A【点睛】本题考查了勾股定理；熟练掌握勾股定理，并能进行推理计算是解决问题的关键，注意分类讨论，∴()()22340a b -+-=，∴30a -=，40b -=，解得：3a =，4b =，∵5c =，∴22229165a b c +=+==，∴ABC 为直角三角形．故答案为：直角三角形．【点睛】本题考查的是利用完全平方公式分解因式，非负数的性质，勾股定理的应用，利用非负数的性质求解3a =，4b =是解本题的关键．题型四勾股定理的逆定理的实际应用【例4】．如图，某住宅小区在施工后留下了一块空地，已知4=AD 米，3CD =米，13AB =米，12BC =米，90ADC ∠=︒，小区为美化环境，欲在空地上铺草坪．若草坪每平方米30元，则用该草坪铺满这块空地需花费多少元？【答案】铺满这块空地共需花费720元【分析】连接AC ，在Rt ACD △中利用勾股定理计算出AC 长，再利用勾股定理逆定理证明90ACB ∠=︒，再利用ACB ACD S S - 可得草坪面积，然后再计算花费即可．【解析】连接AC ，在Rt ACD △中，4=AD 米，3CD =米，222223425AC CD AD =+=+=，∴5AC =，1．为了绿化环境，我市某中学有一块四边形的空地ABCD ，如图所示，学校计划在空地上种植草皮，经测量903m 4m 12m 13m A AB DA BC CD ∠=︒====，，，，．(1)求出空地ABCD 的面积．(2)若每种植1平方米草皮需要300元，问总共需投入多少元？【答案】(1)空地ABCD 的面积为236m ；(2)总共需投入10800元．【分析】（1）连接BD ．在Rt △ABD 中可求得BD 的长，再由勾股定理的逆定理证得CBD △是直角三角形，且90DBC ∠=︒；根据三角形面积公式即可求解；（2）根据总费用=面积×单价解答即可．【解析】（1）解：连接BD ．在Rt △ABD 中，222222345BD AB AD =+=+=．在CBD △中，22221312CD BC ==，，而22212513+=，即222BC BD CD +=，∴CBD △是直角三角形，且90DBC ∠=︒，A ．7B ．8【答案】D ∵3,1OC BC ==∴223110OA OB ==+=，(1)写出数轴上点A 表示的数；(2)比较点A 表示的数与 1.5-的大小；由勾股定理得：2222OC OH CH =+=+以O 为圆心，OC 长为半径画弧，交x 轴的正半轴于点【答案】直角【分析】结合网格图，先根据勾股定理求出AB【解析】由图可知，2∴222AB BC AC +=，∴ABC 是直角三角形，故答案为：直角．【点睛】本题考查的是勾股定理及其逆定理的知识，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．A ．101313【答案】D【分析】根据勾股定理计算【解析】解：由勾股定理得：∵1332ABC S =⨯-⨯△∴1722AC BD ⋅=，∴137BD ⋅=，∴71313BD =，故选：D ．【点睛】本题考查了网格与勾股定理，三角形的面积的计算，掌握勾股定理是解题的关键．2．如图，小正方形边长为(1)在图1中以格点A为顶点画一个面积为(2)①在图2中以格点E为顶点画一个的面积．②求出EFG【答案】(1)见解析正方形ABCD即为所求作的图形；（2）①如图2，EF=，EG=② 2222EF EG FG∴+=∴EFG为直角三角形【解析】解：∵在ABC 中，90A C ∠+∠=︒，∴90B Ð=°，∴ABC 为直角三角形，则根据勾股定理得：222a c b +=．故选：C ．【点睛】此题考查了勾股定理，熟练掌握勾股定理是解题的关键．巩固训练：1．如图，ABC 中，90BAC ∠=︒，点A 向上平移后到A '，得到A BC ' ．下面说法错误的是（）A ．ABC 的内角和仍为180︒B ．BAC BAC '∠<∠C ．222AB AC BC +=D ．222A B A C BC ''+<【答案】D 【分析】根据三角形的内角和定理，勾股定理以及平移的性质对各选项分析判断后利用排除法求解．【解析】解：A 、△A ′BC 的内角和仍为180°正确，故本选项正确，不合题意；B 、∵∠BA ′C ＜90°，∠BAC =90°，∴∠BA ′C ＜∠BAC 正确，故本选项正确，不合题意；C 、由勾股定理，AB 2+AC 2=BC 2，故本选项正确，不合题意；D 、应为A ′B 2+A ′C 2＞BC 2，故本选项错误，符合题意．故选：D ．【点睛】本题考查了勾股定理，三角形的内角和定理，以及平移，熟记定理并准确识图是解题的关键．2．如图，在ABC 中，AB AC >，AH BC ⊥于H ，M 为AH 上异于A 的一点，比较AB AC -与MB MC -的大小，则AB AC -（）MB MC -．A ．大于B ．等于C ．小于D ．大小关系不确定【答案】8【分析】分别设三个正方形【解析】解：设正方形由勾股定理得：A ．31B ．63C ．65D ．67【答案】B 【分析】由已知图形观察规律，即可得到第五代勾股树中正方形的个数．【解析】解：由题意可知第一代勾股树中正方形有123+=（个），第二代勾股树中正方形有21227++=（个），第三代勾股树中正方形有23122215+++=（个），由此推出第五代勾股树中正方形有234512222263+++++=（个）故选：B ．【点睛】本题考查了图形类规律探索的相关问题，仔细观察从图中找到规律是解题的关键．【例10】．如图是由“赵爽弦图”变化得到的，它由八个全等的直角三角形拼接而成，记图中正方形正方形EFGH 、正方形MNKT 的面积分别为123S S S 、、．若12318S S S ++=A ．125B ．6C ．5D ．154【答案】B【解析】先设每个直角三角形的长直角边为关于a 、b 的方程，然后整理化简，即可求得【解答】解：设每个直角三角形的长直角边为∴()()()222218a b a b a b ++++-=，∴2222222218a ab b a b a ab b ++++++=-，∴()22318a b +=，∴226a b +=，∴2226S a b =+=，故选：B ．【点评】本题考查勾股定理的应用、正方形的面积，解答本题的关键是明确勾股定理的内容，可以写出相应的等式．【答案】=【解析】连接AC ，分别在Rt 从而可得22AB BC AD +=【分析】解：连接AC ，∵90ABC ADC ∠=∠=︒，∴222AB BC AC +=，2ADA．8B．22【答案】C【分析】分别设中间两个正方形和最大正方形的边长为22218==即最大正方形的面积为z x y+【解析】解：设中间两个正方形的边长分别为222==；x+23133．如图，有一个面积为1的正方形，经过一次“生长”后，在他的左右肩上生出两个小正方形，其中，三个正方形围成的三角形是直角三角形，再经过一次“生长”后，就变成了如图所示的形状，若继续“生长”下去，它将变得“枝繁叶茂”，请你算出“生长”了2023次后形成的图形中所有的正方形的面积和是（）A ．2024B ．2023C ．2022D ．1【答案】A 【分析】根据勾股定理和正方形的面积公式，知“生长”1次后，以直角三角形两条直角边为边长的正方形的面积和等于以斜边为边长的正方形的面积，即所有正方形的面积和是212⨯=；“生长”2次后，所有的正方形的面积和是313⨯=，推而广之即可求出“生长”2023次后形成图形中所有正方形的面积之和．【解析】解：设直角三角形的是三条边分别是a ，b ，c ．根据勾股定理，得222+=a b c ，即1A B C S S S +==正方形正方形正方形．“生长”1次后，以直角三角形两条直角边为边长的正方形的面积和等于以斜边为边长的正方形的面积，即所有正方形的面积和是212⨯=；“生长”2次后，所有的正方形的面积和是313⨯=，“生长”3次后，所有的正方形的面积和是414⨯=，…“生长”了2023次后形成的图形中所有的正方形的面积和是202412024⨯=．故选：A ．【点睛】能够根据勾股定理发现每一次得到新正方形的面积和与原正方形的面积之间的关系是解本题的关键．4．勾股定理是数学定理中证明方法最多的定理之一，也是用代数思想解决几何问题最重要的工具之一．下列图形中可以证明勾股定理的有（）A ．①③B ．②③C ．②④D ．①④【答案】D 【分析】利用同一个图形的面积的不同表示方法进行验证即可．【解析】解：①()()22211222S a b a ab b =+=++梯形，(2111122222S ab ab c ab c =++=+梯形22A ．5B 【答案】C，．B．C．D．【答案】A【分析】根据赵爽弦图证明勾股定理的方法即可求解．【解析】解：个全等的直角三角形和中间一个小正方形拼成一个大正方形，直角三角形中较长的直角边为A．300m B．400m【答案】A【分析】根据勾股定理：两直角边的平方和等于斜边的平方计算判断．△【解析】解：如图，Rt ABC1．海洋热浪对全球生态带来了严重影响，全球变暖导致华南地区汛期更长、降水强度更大，使得登录广东的台风减少，但是北上的台风增多．如图，一棵大树在一次强台风中距地面5m处折断，倒下后树顶端着地点A距树底端B的距离为12m，这棵大树在折断前的高度为（）A．10m B．15m C．18m D．20m∴2213AC AB BC =+=，∴这棵大树在折断前的高度为13+故选C ．【点睛】本题考查勾股定理的应用，熟练掌握勾股定理是解题的关键．A ．213【答案】B 【分析】沿过点的最短路程，求出【解析】解：如图所示：沿过【点睛】本题考查勾股定理的应用求解是解题的关键．3．将一根长为17cm则x的取值范围是（【点睛】本题考查了勾股定理的应用，能够读懂题意，确定出4．一棵高10m的大树倒在了高面向下滑动，请回答下列各题．(1)如果大树的顶端沿着墙面向下滑动了(2)如果大树的顶端沿着墙面向下滑动了【答案】(1)是，理由见解析(2)不一定，理由见解析【点睛】本题考查勾股定理的实际应用，理解题意，利用勾股定理求得线段长度是解题的关键．的点A．20【答案】B【分析】化曲为直，利用勾股定理解决．【解析】解：把玻璃杯的侧面展开，如图，把点D，故选：B【点睛】本题考查了勾股定理的应用，根据题意把圆柱展开，化曲为直是解决问题的关键．6．为了积极响应国家新农村建设的号召，遂宁市某镇政府采用了移动宣讲的形式进行广播宣传．如图，笔直的公路MN的一侧点A处有一村庄，村庄到公路到广播宣传，宣讲车P在公路MN(1)村庄能否听到广播宣传?请说明理由．(2)已知宣讲车的速度是200m/min，如果村庄能听到广播宣传，那么总共能听多长时间【答案】(1)村庄能听到广播宣传，理由见解析(2)8min【点睛】本题考查了勾股定理的应用，结合生活实际，便于更好地理解题意是解题的关键．7．在海平面上有A，B，C三个标记点，其中A在的南偏西36︒方向上，与C的距离是600海里．(1)求点A 与点B 之间的距离；(2)若在点C 处有一灯塔，灯塔的信号有效覆盖半径为处有一艘轮船准备沿直线向点多能收到多少次信号？（信号传播的时间忽略不计）【答案】(1)1000AB =∵CH AB ⊥；∴90CHB ∠︒＝；∵21ABC S AC BC =⋅= ∴480CH ＝；A．7B．【答案】A【分析】先根据勾股定理求出长上的一点，将【答案】52【分析】首先根据勾股定理求出【解析】∵90C ∠=︒，∴22AC AB BC =-=A．423-B．【答案】A【分析】由正方形ABCD可得==，利用勾股定理可求CD DF2(1)求AD的长；是直角三角形．(2)求证：ABC【答案】(1)16(1)试判断ADC △的形状，并说明理由；(2)求四边形ABCD 的面积【答案】(1)ADC △是直角三角形，理由见解析(2)44【分析】（1）在Rt ABC △(1)求证：222AD BE DE +=；(2)若2EB AD =，求DE AD的值．【答案】(1)证明见解析(2)5DE AD=，从而可得答案∵在ABC 中，AC BC =，90ACB ∠=︒，∴45CAB B ∠=∠=︒，∴45FAC ∠=︒，∴()SAS CAF CBE ≌，．用四个全等的直角三角形拼成如图①所示的大正方形，中间也是一个正方形，它是美丽的弦图，其中四(1)结合图①，求证：222a b c.+=(2)如图②，将这四个全等的直角三角形无缝隙无重叠地拼接在一起，得到图形OB=．求该图形的面积．周长为24，3【答案】(1)证明见解析(2)24【分析】（1）由图形可知，大正方形面积等于中间小正方形面积与四个完全相同的直角三角形的面积的和，(1)AC=______；是否为直角三角形，并说明理由．(2)判断ABC⊥，(3)过点A作AE AB【答案】(1)53+；是直角三角形，理由见解析；(2)ABC(1)请运用公式计算点()4,2M 和点(2,N (2)在（1）的条件下，点O 为原点，求 【答案】(1)13(2)1335+【分析】（1）利用平面直角坐标系中两点之间的距离公式直接计算。

AB Ca b c弦股勾勾股定理（知识点）【知识要点】1. 勾股定理的概念：如果直角三角形的两直角边长分别为a ，b ，斜边长为c ，那么 a 2＋b 2＝c 2. 即直角三角形两直角边的平方和等于斜边的平方。

2. 勾股定理的逆定理：如果三角形的三边长a ，b ，c 有下面关系：a 2＋b 2＝c 2，那么这个三角形是直角三角形，其中c 为斜边。

3. 勾股数：①满足a 2＋b 2＝c 2的三个正整数叫做勾股数（注意：若a ，b ，c 、为勾股数，那么ka ，kb ，kc 同样也是勾股数组。

）②记住常见的勾股数可以提高解题速度，如3,4,5；6,8,10；5,12,13；7,24,25；8,15,17等 ③用含字母的代数式表示n 组勾股数： 221,2,1n n n -+（2,n ≥n 为正整数）；2221,22,221n n n n n ++++（n 为正整数） 2222,2,m n mn m n -+（,m n >m ，n 为正整数）4.命题、定理、证明⑴ 命题的概念：判断一件事情的语句，叫做命题。

理解：命题的定义包括两层含义：（1）命题必须是个完整的句子；（2）这个句子必须对某件事情做出判断。

⑵ 命题的分类（按正确、错误与否分） 真命题（正确的命题） 命题假命题（错误的命题）所谓正确的命题就是：如果题设成立，那么结论一定成立的命题。

所谓错误的命题就是：如果题设成立，不能证明结论总是成立的命题。

⑶ 公理：人们在长期实践中总结出来的得到人们公认的真命题，叫做公理。

⑷ 定理：用推理的方法判断为正确的命题叫做定理。

⑸ 证明：判断一个命题的正确性的推理过程叫做证明。

⑹ 证明的一般步骤 ① 根据题意，画出图形。

② 根据题设、结论、结合图形，写出已知、求证。

③ 经过分析，找出由已知推出求证的途径，写出证明过程。

5.判断直角三角形：（1）有一个角为90°的三角形是直角三角形。

勾股定理复习一．知识归纳１．勾股定理：直角三角形两直角边旳平方和等于斜边旳平方；表达措施：假如直角三角形旳两直角边分别为，，斜边为，那么a b c 222a b c +=２.勾股定理旳证明，常见旳是拼图旳措施　①图形进过割补拼接后，只要没有重叠，没有空隙，面积不会变化②根据同一种图形旳面积不一样旳表达措施，列出等式，推导出勾股定理常见措施如下：措施一：，4EFGH S S S ∆+=正方形正方形A B C D 2214()2ab b a c ⨯+-=，化简可证．措施二：四个直角三角形旳面积与小正方形面积旳和等于大正方形旳面积．四个直角三角形旳面积与小正方形面积旳和为 221422S ab c ab c =⨯+=+大正方形面积为因此222()2S a b a ab b =+=++222a b c +=措施三：，，化简得证1()()2S a b a b =+⋅+梯形2112S 222ADE ABE S S ab c ∆∆=+=⋅+梯形３.勾股定理旳合用范围：勾股定理揭示了直角三角形三条边之间所存在旳数量关系，它只合用于直角三角形，因而在应用勾股定理时，必须明了所考察旳对象是直角三角形４.勾股定理旳应用：勾股定理可以协助我们处理直角三角形中旳边长旳计算或直角三角形中线段之间旳关系旳证明问题．在使用勾股定理时，必须把握直角三角形旳前提条件，理解直角三角形中，斜边和直角边各是什么，以便运用勾股定理进行计算，应设法添加辅助线（一般作垂线），构造直角三角形，以便对旳使用勾股定理进行求解．①已知直角三角形旳任意两边长，求第三边。

在中，，则，ABC ∆90C ∠=︒c =b =，a =②懂得直角三角形一边，可得此外两边之间旳数量关系cba HG FEDCBAbacbac cabcab a bccb aE D CBA③可运用勾股定理处理某些实际问题５.勾股定理旳逆定理　假如三角形三边长，，满足，那么这个三角形是直角三角形，其中为斜边。

勾股定理全章复习类型一：已知两边求第三边例1：⑴已知6AC =，8BC =．求AB 的长⑵已知17AB =，15AC =，求BC 的长变式练习：已知两条线段的长分别为15和8，当第三条线段取整数_____时，这三条线段能围成一个直角三角形．类型二：判断三角形形状例1：下列线段不能组成直角三角形的是( )．A. B. C. D. 2、若三角形的三边长为a ，b ，c ，且满足等式(a ＋b)2－c 2＝2ab ，则此三角形是______三角形．变式练习1：判断由线段组成的三角形是不是直角三角形．（1）＝7，＝24，＝25；（2）＝，＝1，＝；（3），，()；2、若边长为a 的正方形的面积等于长为b ＋c ，宽为b －c 的长方形的面积，则以a ，b ，c 为三边长的三角形是______三角形．3、已知△ABC 的三边为a ，b ，c ，且a ＋b ＝7，ab ＝12，c ＝5，试判定△ABC 的形状．类型三：勾股树及变形例1：如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边和长为7cm,则正方形A ，B ，C ，D 的面积之和为___________cm 2。

6,8,10a b c ===3,2,1===c b a 43,1,45===c b a 6,3,2===c b a a b c ，，a b c a 43b c 3422a m n =-22b m n =+2c mn =0m n >> A B C D7cm15题 变式练习：如图，正方形ABCD 的边长为2，其面积标记为S 1，以CD 为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为S 2……按照此规律继续下去，则S 2018的值为( )A ．(22)2015 B ．(22)2016 C ．(12)2015 D ．(12)2016 类型四：勾股定理证明的应用例1：如图1，分别以直角△ABC 的三边AB ，BC ，CA 为直径向外作半圆.设直线AB 左边阴影部分的面积为S 1，右边阴影部分的面积和为S 2，则（ ）A S 1＝S 2B S 1＜S 2C S 1＞S 2D 无法确定变式练习：如图，Rt△ABC 中，AC =5，BC =12，分别以它的三边为直径向上作三个半圆，则阴影部分面积为 ．类型五：数轴表示数例题1：在数轴上表示√17变式练习：如图，数轴上有两个直角三角形Rt △ABO 、Rt △CDO ，OA 、OC 是斜边，且OB=1，AB=1，CD=1，OD=2，分别以O 为圆心，OA 、OC 为半径画弧交x 轴于E 、F ，则E 、F 分别对应的数是 。

第02讲勾股定理逆定理课程标准学习目标①勾股定理逆定理②勾股数③勾股定理的应用1.掌握勾股定理的逆定理内容，并能够熟练的运用它来判断直角三角形。

2.掌握勾股数并能够判断勾股数。

3.能够在各类实际问题中熟练应用勾股定理。

知识点01勾股定理逆定理1.勾股定理逆定理内容：在△ABC 中，如果三角形的三边分别是c b a ，，且满足222c b a =+，则该三角形一定是有一个直角三角形且∠C 是直角。

勾股定理的逆定理用于判断一个三角形是不是直角三角形。

2.直角三角形的判定①勾股定理逆定理②三角形中有一个角是90°。

③三角形中有两个角之和为90°。

【即学即练1】1．以下列数据为长度的线段中，可以构成直角三角形的是（）A．1，2，3B．2，3，4C．1，，D．，3，5【分析】由勾股定理的逆定理，只要验证两小边的平方和等于最长边的平方即可．【解答】解：A、12+22≠32，不能构成直角三角形，故不符合题意；B、22+32≠42，不能构成直角三角形，故不符合题意；C、12+（）2＝（）2，能构成直角三角形，故符合题意；D、（）2+32≠52，不能构成直角三角形，故不符合题意．故选：C．【即学即练2】2．如图，在△ABC中，AC＝6cm，BC＝8cm，AB＝10cm，AB的垂直平分线交AB于点D，交BC于点E．（1）试说明△ABC为直角三角形．（2）求CE的长．【分析】（1）先计算AC2+BC2＝62+82＝100，AB2＝102＝100，再利用勾股定理的逆定理可得结论；（2）设CE长为x cm，则BE＝（8﹣x）cm．由DE垂直平分AB，可得AE＝BE＝8﹣x．再利用勾股定理建立方程即可．【解答】（1）证明：∵AC2+BC2＝62+82＝100，AB2＝102＝100，∴AC2+BC2＝AB2，∴△ABC为直角三角形．（2）解：设CE长为x cm，则BE＝（8﹣x）cm．∵DE垂直平分AB，∴AE＝BE＝8﹣x．在Rt△ACE中，由勾股定理得x2+62＝（8﹣x）2，解得，所以CE的长为．知识点02勾股数1.勾股数的定义：满足勾股定理：即222cba=+的三个正整数称为勾股数。