32探究弹力与弹簧伸长的关系
- 格式:docx
- 大小:468.58 KB
- 文档页数:9

实验专题:探究弹簧弹力和弹簧伸长量的关系答案解析答案解析1.【答案】(1)C(2)等于【解析】(1)因为弹簧是被放在水平桌面上测得的原长,然后把弹簧竖直悬挂起来后,由于重力的作用,弹簧的长度会增大,所以图线应出现x轴上有截距,C正确,A、B、D错误.(2)如果将指针固定在A点的下方P处,在正确测出弹簧原长的情况下,再作出x随F变化的图象,则在图象上x的变化量不变,得出弹簧的劲度系数与实际值相等.2.【解析】(1)F-L图线如图所示:(2)弹簧的原长L0即弹力为零时弹簧的长度,由图象可知,L0=5×10-2m=5 cm.劲度系数为图象直线部分的斜率,k=20 N/m.(3)记录数据的表格如下表(4)优点:可以避免弹簧自身重力对实验的影响.缺点:弹簧与桌面及绳子与滑轮间存在的摩擦会造成实验误差.3.【解析】(1)在做实验的时候一般步骤为先组装器材,然后进行实验,最后数据处理,故顺序为CBDAEF.(2)①根据描点法,图象如图所示②、③根据图象,该直线为过原点的一条直线,即弹力与伸长量成正比,即F=kx=0.43x.式中的常数表示弹簧的劲度系数,即表示使弹簧伸长或者压缩1 cm所需的外力大小为0.43 N.4.【答案】(1)如图所示30F弹=30Δx(2)B(3)A【解析】(1)如图所示,直线的斜率的倒数表示弹簧的劲度系数,即k=,代入数据得kA =N/m≈30 N/m,所以弹簧的弹力大小F弹跟弹簧伸长量Δx的函数关系是F弹=30Δx.5.【解析】(1)描点作图,如图所示:(2)图象的斜率表示劲度系数,故有:k==N/m=50 N/m(3)图线与L轴的交点坐标表示弹簧不挂钩码时的长度,其数值大于弹簧原长,因为弹簧自身重力的影响.6.【答案】(1)6.93(2)A(3)弹簧受到的拉力超过了其弹性限度【解析】(1)弹簧伸长后的总长度为14.66 cm,则伸长量Δl=14.66 cm-7.73 cm=6.93 cm.(2)逐一增挂钩码,便于有规律地描点作图,也可避免因随意增加钩码过多超过弹簧的弹性限度而损坏弹簧.(3)AB段明显偏离直线OA,伸长量Δl不再与弹力F成正比,是超出弹簧的弹性限度造成的.7.【解析】(1)根据题意知,刻度尺的最小刻度为1毫米.读数时,应估读到毫米的十分位,故l5、l6记录有误.(2)按(1)中的读数规则,得l3=6.85 cm,l7=14.05 cm.(3)根据题中求差方法,可知d4=l7-l3=7.20 cm(4)根据l4-l0=4Δl=d1,l5-l1=4Δl=d2,l6-l2=4Δl=d3,l7-l3=4Δl=d4,有Δl==1.75 cm.(5)根据胡克定律F=kx得mg=kΔl,k==N/m=28 N/m8.【答案】(1)450(2)10【解析】(1)当F=0时,弹簧的长度即为原长,由胡克定律可知图象的斜率表示劲度系数大小.(2)弹簧秤的示数为3 N,则伸长量为3/50=0.06 m,则长度为10 cm.9.【解析】(1)描点作出图象,如下图所示.(2)图象跟坐标轴交点的物理意义表示弹簧原长.由图象可知,弹簧的劲度系数应等于直线的斜率,即k==200 N/m.10.【答案】(1)竖直(2)稳定L3 1 mm(3)Lx(4)4.910【解析】(1)为保证弹簧的形变只由砝码和砝码盘的重力产生,所以弹簧轴线和刻度尺均应在竖直方向.(2)弹簧静止稳定时,记录原长L0;表中的数据L3与其他数据有效位数不同,所以数据L3不规范,标准数据应读至cm位的后两位,最后一位应为估读值,精确至0.1 mm,所以刻度尺的最小分度为1 mm.(3)由题图知所挂砝码质量为0时,x为0,所以x=L-Lx(L为弹簧长度).(4)由胡克定律F=kΔx知,mg=k(L-Lx),即mg=kx,所以图线斜率即为弹簧的劲度系数k==N/m=4.9 N/m同理,砝码盘质量m==kg=0.01 kg=10 g11.【解析】(1)根据表格中的各组数据在坐标纸上标出相应的点,然后用平滑曲线连接这些点,作出的图象如图所示.(2)根据作出的图线可知,钩码质量在0~500 g范围内图线是直线,表明弹力大小与弹簧伸长量关系满足胡克定律.在这个范围内的曲线上找到相距较远的两点,利用这两点的坐标值计算弹簧的劲度系数k==N/m=25.00 N/m.12.【解析】(1)本题考查探究弹簧弹力与形变关系的实验,意在考查考生对实验步骤的识记、实验数据的处理方法、分析归纳能力.根据实验先后顺序可知,实验步骤排列为CBDAEF.(2)②由图象可得k==0.43 N/cm,所以F=0.43x(N).13.【答案】(1)10(2)200(3)b【解析】(1)当F=0时,弹簧长度为原长,由题图得,原长为10 cm.(2)由公式F=kx得k===N/m=200 N/m(3)当弹簧长度小于原长时,处于压缩状态,故是图线b14.【答案】(1)弹簧测力计刻度尺(2)kFL(3)控制变量法(4)12.5【解析】(1)用弹簧测力计测量力的大小,用刻度尺测量长度.(2)由题目所给数据分析可知:当力一定时,伸长量和长度成正比;当长度一定时,伸长量和力成正比,故有x=kFL(取一组数据验证,式中的k不为零).(3)研究伸长量与拉力、长度的关系时,可以先控制其中一个量不变,如长度不变,再研究伸长量和拉力的关系,这种方法称为控制变量法.这是物理实验中的一个重要研究方法.(4)代入表中数据把式中的k求出,得k=0.000 8 N-1,再代入已知数据,L=20 cm,x=0.2 cm,可求得最大拉力F=12.5 N.15.【答案】CBDAEFG【解析】根据实验的实验操作过程应先安装仪器,再挂钩码然后记录数据,分析数据,最后整理即可,排列先后顺序为CBDAEFG.。



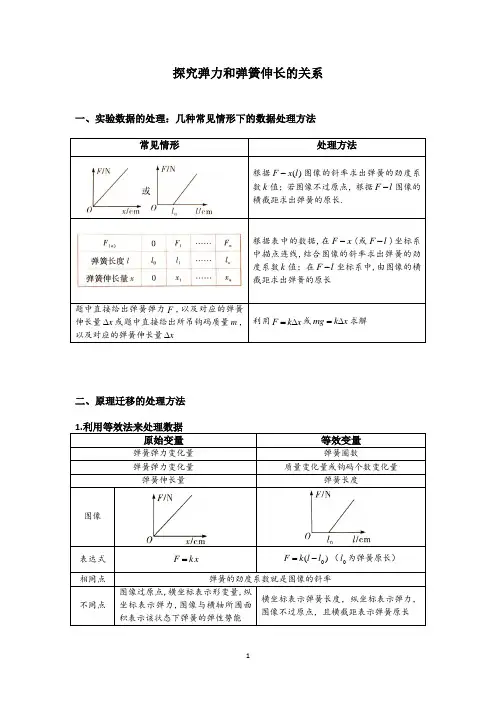
探究弹力和弹簧伸长的关系一、实验数据的处理:几种常见情形下的数据处理方法常见情形 处理方法根据)(l x F -图像的斜率求出弹簧的劲度系数k 值;若图像不过原点,根据l F -图像的横截距求出弹簧的原长.根据表中的数据,在x F -(或l F -)坐标系中描点连线,结合图像的斜率求出弹簧的劲度系数k 值;在l F -坐标系中,由图像的横截距求出弹簣的原长题中直接给出弹簧弹力F ,以及对应的弹簧伸长量x ∆或题中直接给出所吊钩码质量m ,以及对应的弹簧伸长量x ∆ 利用x k F ∆=或x k mg ∆=求解二、原理迁移的处理方法1.利用等效法来处理数据原始变量等效变量弹簧弹力变化量 弹簧圈数弹簧弹力变化量 质量变化量或钩码个数变化量弹簧伸长量 弹簧长度图像表达式 kx F =)(0l l k F -=(0l 为弹簧原长)相同点 弹簧的劲度系数就是图像的斜率不同点图像过原点,横坐标表示形变量,纵坐标表示弹力,图像与横轴所围面积表示该状态下弹簧的弹性势能横坐标表示弹簧长度,纵坐标表示弹力,图像不过原点,且横截距表示弹簧原长2.弹簧串、并联时劲度系数的处理方法实验装置 实验参量实验结论两个弹簧的劲度系数分别为1k 、2k ,两个弹簧的伸长量分别为1x 、2x ,总伸长量为x ,重物的重力为mg对于1k ,有mg x k =11,得到11k mgx =。
对于2k ,有mg x k =22,得到22k mgx =。
对于整体,mg kx =,21x x x +=,得2121k k k k k +=两个弹簧的劲度系数均为1k 两个弹簧的伸长量均为x重物的重力为mg对于一根弹簧,有mg x k 211=,得到12k mg x =。
对于整体,有mg kx =,可得12k k =三、针对练习1、小张同学做“探究弹簧弹力与形变量的关系”的实验。
他先把弹簧放在水平桌面上,量出弹簧原长为0 4.20m L =,再将弹簧按图甲的装置将弹簧竖直悬挂。
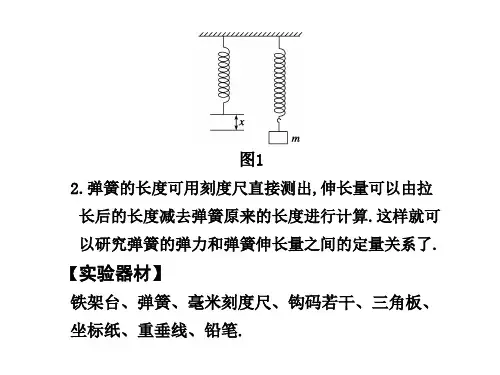

实验二探究弹力和弹簧伸长的关系1.实验原理弹簧受到拉力作用会伸长,平衡时弹簧产生的弹力和外力大小相等;弹簧的伸长量越大,弹力也就越大.2.实验器材铁架台、弹簧、钩码、刻度尺、坐标纸.3.实验步骤(1)安装实验仪器(如图1所示).图1(2)测量弹簧的伸长量(或总长)及所受的拉力(或所挂钩码的质量),列表作出记录,要尽可能多测几组数据.(3)根据所测数据在坐标纸上描点,以力为纵坐标,以弹簧的伸长量为横坐标.(4)按照在图中所绘点的分布与走向,尝试作出一条平滑的曲线(包括直线),所画的点不一定正好在这条曲线上,但要注意使曲线两侧的点数大致相同.(5)以弹簧的伸长量为自变量,写出曲线所代表的函数,首先尝试一次函数,如果不行再考虑二次函数.1.数据处理(1)列表法将测得的F、x填入设计好的表格中,可以发现弹力F与弹簧伸长量x的比值在误差允许范围内是相等的.(2)图象法以弹簧伸长量x为横坐标,弹力F为纵坐标,描出F、x各组数据相应的点,作出的拟合曲线是一条过坐标原点的直线.(3)函数法弹力F与弹簧伸长量x满足F=kx的关系.2.注意事项(1)不要超过弹性限度:实验中弹簧下端挂的钩码不要太多,以免弹簧被过分拉伸,超过弹簧的弹性限度.(2)尽量多测几组数据:要使用轻质弹簧,且要尽量多测几组数据.(3)观察所描点的走向:本实验是探究性实验,实验前并不知道其规律,所以描点以后所作的曲线是试探性的,只是在分析了点的分布和走向以后才决定用直线来连接这些点.(4)统一单位:记录数据时要注意弹力及弹簧伸长量的对应关系及单位.3.误差分析(1)钩码标值不准确、弹簧长度测量不准确带来误差.(2)画图时描点及连线不准确也会带来误差.命题点一教材原型实验处理实验数据的方法1.列表分析法:分析列表中弹簧拉力F与对应弹簧的形变量Δx的关系,可以先考虑F和Δx的乘积,再考虑F和Δx的比值,也可以考虑F和(Δx)2的关系或F和Δx的关系等,结论:FΔx 为常数.2.图象分析法:作出F-Δx图象,如图2所示.此图象是过坐标原点的一条直线,即F和Δx 成正比关系.图2作图的规则:(1)要在坐标轴上标明轴名、单位,恰当地选取纵轴、横轴的标度,并根据数据特点正确确定坐标起点,使所作出的图象几乎占满整个坐标图纸.若弹簧原长较长,则横坐标起点可以不从零开始选择.(2)作图线时,尽可能使直线通过较多坐标描点,不在直线上的点也要尽可能对称分布在直线的两侧(若有个别点偏离太远,则是因偶然误差太大所致,应舍去).(3)要注意坐标轴代表的物理量的意义,注意分析图象的斜率、截距的意义.例1(2015·福建理综·19(1))某同学做“探究弹力和弹簧伸长量的关系”的实验.(1)图3甲是不挂钩码时弹簧下端指针所指的标尺刻度,其示数为7.73 cm;图乙是在弹簧下端悬挂钩码后指针所指的标尺刻度,此时弹簧的伸长量Δl为________cm;图3(2)本实验通过在弹簧下端悬挂钩码的方法来改变弹簧的弹力,关于此操作,下列选项中规范的做法是________;(填选项前的字母)A.逐一增挂钩码,记下每增加一只钩码后指针所指的标尺刻度和对应的钩码总重B.随意增减钩码,记下增减钩码后指针所指的标尺刻度和对应的钩码总重(3)图丙是该同学描绘的弹簧的伸长量Δl与弹力F的关系图线,图线的AB段明显偏离直线OA,造成这种现象的主要原因是____________________________.答案(1)6.93 (2)A (3)钩码重力超过弹簧弹力范围解析(1)由题图乙知,读数为14.66 cm,所以弹簧伸长量为(14.66-7.73) cm=6.93 cm;(2)若随意增减钩码,会使作图不方便,有可能会超出弹簧形变范围,所以应逐一增挂钩码,选项A 正确.(3)由题图丙知AB段伸长量与弹力不成线性关系,是因为钩码重力超过弹簧弹力范围.变式1某学生做“探究弹力和弹簧伸长的关系”的实验.实验时把弹簧竖直悬挂起来,在下端挂钩码,每增加一只钩码均记下对应的弹簧的长度x,数据记录如下表所示.钩码个数01234567弹力F/N0 1.0 2.0 3.0 4.0 5.0 6.07.0弹簧伸长的长度x/cm0 2.00 3.98 6.027.979.9511.8013.50 (1)根据表中数据在图4中作出F-x图线.图4(2)根据F-x图线可以求得弹簧的劲度系数为________ N/m.(3)估测弹簧弹力为5 N时弹簧的弹性势能为________ J.答案(1)如图所示(2)50 (3)0.25命题点二创新实验——器材与方法的创新本实验一般是在教材实验原理的基础上设计新情景进行考查,因此,要在教材实验的基础上注重迁移创新能力的培养,善于用教材中实验的原理、方法和技巧处理新问题.高考考情演变装置时代化求解智能化1.弹力的获得:弹簧竖直悬挂,重物的重力作为弹簧的拉力,存在弹簧自重的影响→弹簧水平使用,重物的重力作为弹簧的拉力,消除了弹簧自重的影响. 2.图象的获得:由坐标纸作图得F -x 图象→由传感器和计算机输入数据直接得F -x 图象.例2 (2014·新课标全国Ⅱ·23)某实验小组探究弹簧的劲度系数k 与其长度(圈数)的关系.实验装置如图5所示:一均匀长弹簧竖直悬挂,7个指针P 0、P 1、P 2、P 3、P 4、P 5、P 6分别固定在弹簧上距悬点0、10、20、30、40、50、60圈处;通过旁边竖直放置的刻度尺,可以读出指针的位置,P 0指向0刻度.设弹簧下端未挂重物时,各指针的位置记为x 0;挂有质量为0.100 kg 的砝码时,各指针的位置记为x .测量结果及部分计算结果如下表所示(n 为弹簧的圈数,取重力加速度为9.80 m/s 2).已知实验所用弹簧总圈数为60,整个弹簧的自由长度为11.88 cm.图5P 1 P 2 P 3 P 4 P 5 P 6 x 0(cm) 2.04 4.06 6.06 8.05 10.03 12.01 x (cm) 2.64 5.26 7.81 10.30 12.93 15.41 n 10 20 30 40 50 60 k (N/m)163 56.0 43.6 33.8 28.8 1k(m/N)0.006 10.017 90.022 90.029 60.034 7(1)将表中数据补充完整:________;________.(2)以n 为横坐标,1k 为纵坐标,在图6给出的坐标纸上画出1k—n 图象.图6(3)图6中画出的直线可近似认为通过原点.若从实验中所用的弹簧截取圈数为n 的一段弹簧,该弹簧的劲度系数k 与其圈数n 的关系的表达式为k =________ N/m ;该弹簧的劲度系数k 与其自由长度l 0(单位为m)的关系表达式为k =________ N/m.答案 (1)81.7 0.012 2 (2)见解析图 (3)1.75×103n (在1.67×103n ~1.83×103n 之间均可) 3.47l 0(在3.31l 0~3.62l 0之间均可)解析 (1)根据胡克定律有mg =k (x -x 0),解得k =mg x -x 0=0.100×9.805.26-4.06×10-2N/m ≈81.7N/m ,1k≈0.012 2 m/N.(2)1k-n 图象如图所示(3)根据图象可知,k 与n 的关系表达式为k =1.75×103n N/m ,k 与l 0的关系表达式为k =3.47l 0.变式2 在探究弹簧的弹力与伸长量之间关系的实验中,所用装置如图7甲所示,将轻弹簧的一端固定,另一端与力传感器连接,其伸长量通过刻度尺测得,某同学的实验数据列于下表中:图7伸长量x /(×10-2 m)2.00 4.00 6.00 8.00 10.00 弹力F /N1.502.934.555.987.50(1)以x 为横坐标,F 为纵坐标,在图乙的坐标纸上描绘出能正确反映这一弹簧的弹力与伸长量之间的关系图线.(2)由图线求得这一弹簧的劲度系数为________.(结果保留三位有效数字) 答案 (1)见解析图 (2)75.0 N/m 解析 (1)描点作图,如图所示.(2)根据图象,该直线为过原点的一条倾斜直线,即弹力与伸长量成正比,k =ΔFΔx =75.0 N/m.命题点三 拓展实验——探究弹簧的弹性势能例3 (2016·全国卷Ⅱ·22)某物理小组对轻弹簧的弹性势能进行探究,实验装置如图8所示:轻弹簧放置在光滑水平桌面上,弹簧左端固定,右端与一物块接触而不连接,纸带穿过打点计时器并与物块连接.向左推物块使弹簧压缩一段距离,由静止释放物块,通过测量和计算,可求得弹簧被压缩后的弹性势能.图8(1)实验中涉及到下列操作步骤: ①把纸带向左拉直 ②松手释放物块 ③接通打点计时器电源④向左推物块使弹簧压缩,并测量弹簧压缩量上述步骤正确的操作顺序是________(填入代表步骤的序号).(2)图9中M 和L 纸带是分别把弹簧压缩到不同位置后所得到的实际打点结果.打点计时器所用交流电的频率为50 Hz.由M 纸带所给的数据,可求出在该纸带对应的实验中物块脱离弹簧时的速度为________m/s.比较两纸带可知,________(填“M ”或“L ”)纸带对应的实验中弹簧被压缩后的弹性势能大.图9答案 (1)④①③② (2)1.29 M解析 (1)根据该实验操作过程,正确步骤应为④①③②.(2)物块脱离弹簧时速度最大,v =Δx Δt =2.58×10-20.02 m/s =1.29 m/s ;由动能定理ΔE k =12mv 2,据纸带中打点的疏密知M 纸带获得的最大速度较大,对应的实验中弹簧被压缩后的弹性势能较大.变式3 某同学利用下述装置对轻质弹簧的弹性势能进行探究:一轻质弹簧放置在光滑水平桌面上,弹簧左端固定,右端与一小球接触而不固连.弹簧处于原长时,小球恰好在桌面边缘,如图10所示.向左推小球,使弹簧压缩一段距离后由静止释放,小球离开桌面后落到水平地面.通过测量和计算,可求得弹簧被压缩后的弹性势能.图10回答下列问题:(1)本实验中可认为,弹簧被压缩后的弹性势能E p 与小球抛出时的动能E k 相等.已知重力加速度大小为g .为求得E k ,至少需要测量下列物理量中的________(填正确答案标号). A.小球的质量mB.小球抛出点到落地点的水平距离sC.桌面到地面的高度hD.弹簧的压缩量ΔxE.弹簧原长l 0(2)用所选取的测量量和已知量表示E k ,得E k =______________.(3)图11中的直线是实验测量得到的s -Δx 图线.从理论上可推出,如果h 不变.m 增加,s -Δx 图线的斜率会________(填“增大”、“减小”或“不变”):如果m 不变,h 增加,s -Δx 图线的斜率会________(填“增大”、“减小”或“不变”).由图中给出的直线关系和E k 的表达式可知,E p 与Δx 的__________次方成正比.图11答案 (1)ABC (2)mgs 24h(3)减小 增大 二解析 (1)小球离开桌面后做平抛运动,设桌面到地面的高度为h ,小球抛出点到落地点的水平距离为s ,则有h =12gt 2,s =v 0t ,解得v 0=st =sg2h所以E k =12mv 02=mgs 24h.由此可知需要测量的量有m 、s 、h ,故选A 、B 、C.(2)由(1)的解析知E k =mgs 24h.(3)在Δx 相同的情形下,弹簧的弹性势能相同,由E p =12mv 02可知:①在m 增加时,速度v 0减小,因而h 不变时s 减小,故图线的斜率减小.②m 不变时,v 0不变,h 增加时,时间变长,s 变大,故图线的斜率增大.由s -Δx 图象可知,s 正比于Δx ,即s =k Δx . 则E p =12mv 02=mgs 24h =mgk 24h Δx 2=k ′Δx 2所以E p 与Δx 的二次方成正比.变式4 (2016·四川理综·8Ⅰ)用如图12所示的装置测量弹簧的弹性势能.将弹簧放置在水平气垫导轨上,左端固定,右端在O 点;在O 点右侧的B 、C 位置各安装一个光电门,计时器(图中未画出)与两个光电门相连.先用米尺测得B 、C 两点间距离s ,再用带有遮光片的滑块压缩弹簧到某位置A ,静止释放,计时器显示遮光片从B 到C 所用的时间t ,用米尺测量A 、O 之间的距离x .图12(1)计算滑块离开弹簧时速度大小的表达式是________. (2)为求出弹簧的弹性势能,还需要测量________. A.弹簧原长 B.当地重力加速度 C.滑块(含遮光片)的质量(3)增大A 、O 之间的距离x ,计时器显示时间t 将________. A.增大 B.减小 C.不变答案 (1)v =st(2)C (3)B解析 (1)滑块离开弹簧后做匀速直线运动,v =s t.(2)根据功能关系可得,E p =12mv 2,则还需要测量滑块(含遮光片)的质量,选项C 正确.(3)增大A 、O 之间的距离x ,弹簧的弹性势能增大,滑块离开弹簧后的速度增大,从B 到C 的时间t 将减小,选项B 正确.。

实验二探究弹力和弹簧伸长量的关系班级_______________ 姓名_______________时间______________一、实验目的1.探究弹力和弹簧伸长量的关系.2.学会利用图象法处理实验数据,探究物理规律.二、实验原理1.如图1所示,弹簧在下端悬挂钩码时会伸长,平衡时弹簧产生的弹力与所挂钩码的重力大小相等.2.用刻度尺测出弹簧在不同钩码拉力下的伸长量x,建立直角坐标系,以纵坐标表示弹力大小F,以横坐标表示弹簧的伸长量x,在坐标系中描出实验所测得的各组(x、F)对应的点,用平滑的曲线连接起来,根据实验所得的图线,就可探知弹力大小与伸长量间的关系.三、实验器材__________________、____________、____________、____________、____________、____________、____________四、实验步骤1.将弹簧的一端挂在铁架台上,让其自然下垂,用刻度尺测出________________________,即原长.2.如图所示,在弹簧下端挂质量为m1的钩码,测出此时弹簧的长度l1,记录m1和l1,填入自己设计的表格中.3.改变所挂钩码的质量,测出对应的弹簧长度,记录m2、m3、m4、m5和相应的弹簧长度2、3、4、5,并得出每次弹簧的伸长量1、2、3、4、5.钩码个数长度伸长量x 钩码质量m弹力F0——————12345⋮⋮⋮⋮⋮五、数据处理1.以弹力F(大小等于所挂钩码的重力)为纵坐标,以弹簧的伸长量x为横坐标,用描点法作图.连接各点,得出弹力F随弹簧伸长量x变化的图线.2.以弹簧的伸长量为自变量,写出图线所代表的函数.首先尝试一次函数,如果不行则考虑二次函数.3.得出弹力和弹簧伸长量之间的定量关系,解释函数表达式中常数的物理意义.六、误差分析七、注意事项1.每次增减钩码测量有关长度时,均需保证弹簧及钩码不上下振动而处于静止状态,否则,弹簧弹力将可能与钩码重力不相等.2.弹簧下端增加钩码时,注意不要超过弹簧的限度.3.测量有关长度时,应区别弹簧原长l0、实际总长l及伸长量x三者之间的不同,明确三者之间的关系.4.建立平面直角坐标系时,两轴上单位长度所代表的量值要适当,不可过大,也不可过小.5.描线的原则是,尽量使各点落在描出的线上,少数点分布于线两侧,描出的线不应是折线,而应是平滑的曲线.6.记录数据时要注意弹力及弹簧伸长量的对应关系及单位.THANKS !!!致力为企业和个人提供合同协议,策划案计划书,学习课件等等打造全网一站式需求欢迎您的下载,资料仅供参考。

3.1.2实验:探究弹簧伸长量与弹力关系解析版一、【探究弹簧伸长量与弹力关系知识点梳理】1. 实验原理(1)弹簧的弹力F的测量:弹簧下端悬挂的钩码静止时,弹力大小与所挂钩码的重力大小相等,即F=mg。
(2)弹簧的伸长量x的确定:弹簧的原长l0与挂上钩码后弹簧的长度l可以用刻度尺测出,弹簧的伸长量x=l-l0。
(3)作F-x图像:建立直角坐标系,作出弹簧弹力F与弹簧伸长量x的关系图像,根据图像可以分析弹簧弹力大小和弹簧伸长量之间的关系。
2. 实验步骤(1)按图安装实验装置,用刻度尺测出弹簧下端不挂钩码时弹簧的原长l0。
(2)在弹簧下悬挂一个钩码,平衡时记下弹簧的总长度,并记下钩码的重力。
(3)增加钩码的个数,重复上述实验过程,将数据填入表格,以F表示弹力,l表示弹簧的总长度,x=l-l0表示弹簧的伸长量。
3. 数据处理(1)以弹簧弹力F(大小等于所挂钩码的重力)为纵轴、弹簧的伸长量x为横轴,建立直角坐标系,用描点法作图,得到弹力F随弹簧伸长量x变化的图线。
(2)以弹簧伸长量x为自变量,写出弹力F和弹簧伸长量x之间的函数关系式。
关系式中的常数即弹簧的劲度系数,。
这个常数也可根据F-x图线的斜率求解,k=ΔFΔx【探究弹簧伸长量与弹力关系举一反三练习】1.(多选)在“探究弹簧伸长量与弹力关系”的实验中,下列说法中错误的是()A.测量弹簧原长时必须把弹簧平放于水平桌面B.弹簧竖直悬挂于铁架台的横梁上,刻度尺必须紧靠弹簧固定C.在弹簧下端挂钩码时,不能挂太多钩码,以保证弹簧处于弹性限度内D.挂上重物后应等待弹簧稳定后才能读取此时的长度【答案】AB【详解】A.由于弹簧竖直放置时会有自重的影响,因此不能水平放置测量其原长,而应竖直放置测量其因自重而拉伸后的长度作为原长,故A错误,符合题意;B.弹簧竖直悬挂于铁架台的横梁上,刻度尺应竖直固定在弹簧附近,不能紧靠弹簧固定,故B错误,符合题意;C.在弹簧下端挂钩码时,不能挂太多钩码,以保证弹簧处于弹性限度内,故C正确,不符合题意;D.只有弹簧处于稳定状态,读取的数据才准确,因此在弹簧挂上重物后应等待弹簧稳定后才能读取此时的长度,故D正确,不符合题意。

实验3:探究弹力与弹簧伸长量的关系【例1】以下是某同学所进行的“探究弹力和弹簧伸长量的关系〞的实验步骤:①将一个弹簧的上端固定在铁架台上,竖直悬挂起来,在弹簧下挂一个钩码,记下钩码的质量m1,此时弹簧平衡时,弹力大小为F1=m1g,并用刻度尺测量出此时弹簧的长度L1,并记录到表格中.②再增加钩码,重复上述的操作,逐渐增加钩码的重力,得到多组数据.③以力F为纵坐标,以弹簧的长度L x为横坐标,根据所测的数据在坐标纸上描点.④按坐标纸上所描各点的分布与走向,作出一条平滑的曲线(包括直线).⑤根据图线的特点,分析弹簧的弹力F与弹簧长度L x的关系,并得出实验结论.以上步骤有3处不合理,请将不合理的地方找出来并进行修正.答案以上步骤中第①、②、③①步还应该测出弹簧的原长L0;第②步在增加砝码时要取下砝码,看弹簧是否能恢复原长;第③步,应该以弹簧的形变量为横坐标,因为探究的是弹力和弹簧伸长量的关系.【例2】某同学用如图实所示装置做探究弹力和弹簧伸长量的关系的实验.他先测出不挂砝码时弹簧下端指针所指的标尺刻度,然后在弹簧下端挂上砝码,并逐个增加砝码,测出指针所指的标尺刻度,所得数据列表如下:(重力加速度g=9.8 m/s2砝码质量m/102 g标尺刻度x/10-2 m(1)根据所测数据,在图上作出弹簧指针所指的标尺刻度x与砝码质量m的关系曲线.(2)根据所测得的数据和关系曲线可以判断,在N/m.答案 (1)(2)0~490 g 25【例3】下表是某同学为探究弹簧弹力和伸长量的关系所测的几组数据.弹力F/N伸长量x/cm(1)请你在以下列图实的坐标纸上作出F-x图线.(2)写出曲线所代表的函数式.(3)解释函数表达式中常量的物理意义.(4)假设弹簧的原长为40 cm,并且以弹簧的总长为自变量,请你写出它的函数式.答案 (1)如以下列图所示(2)F=20x+0.04 (3)劲度系数 (4)F=20L x【例4】用金属制成的线材(如钢丝、钢筋)受到拉力会伸长,十七世纪英国物理学家胡克发现:金属丝或金属杆在弹性限度内它的伸长与拉力成正比,这就是著名的胡克定律.这一发现为后人对材料的研究奠定了重要根底.现有一根用新材料制成的金属杆,长为4 m,横截面积为0.8 cm2,设计要求它受到拉力后的伸长不超过原长的1/1 000,问最大拉力多大?由于这一拉力很大,杆又较长,直接测试有困难,选用同种材料制成样品进行测试,通过测试取得数据如下:(1)测得结果说明线材受拉力作用后,其伸长与材料的长度成,与材料的截面积成.(2)上述金属细杆承受的最大拉力为N.答案 (1)正比反比 (2)104【例5】某同学为了研究弹簧的弹性势能E p跟弹簧的形变量x之间的关系,设计了这样一个实验:在固定于地面的光滑的桌面上靠近桌边处,将弹簧的一端固定,用一只小球压缩弹簧,然后释放小球弹出,小球弹出后刚好离开桌面做平抛运动,测出弹簧的压缩量x,求出小球被弹出时的速度,算出对应的动能E k(认为等于弹簧的弹性势能),从而研究E p和x间的函数关系.该实验中除上述器材外还需的测量仪器有:,必须测量的物理量有.答案刻度尺、天平水平距离l、桌面的高度h、弹簧的形变量x、小球的质量m“探究弹力和弹簧伸长量的关系〞实验中,他先把弹簧平放在桌面上使其自然伸长,用直尺测出弹簧的原长l0,再把弹簧竖直悬挂起来,挂上钩码后测出弹簧伸长后的长度l,把l-l0作为弹簧的伸长量x.这样操作,由于弹簧自身重力的影响,最后画出的图线可能是以下列图中的哪一个( )答案 C“探究弹力和弹簧伸长量的关系〞的实验中关于操作步骤的先后顺序,以下说法正确的选项是( )A.先测量原长,后竖直悬挂B.先竖直悬挂,后测量原长答案 BD3.“探究弹力和弹簧伸长量的关系〞的实验中,选用的螺旋弹簧如以下列图甲所示.(1)将弹簧的上端O点固定悬吊在铁架台上,旁边置一刻度尺,刻度尺的零刻线跟O点对齐,在弹簧的下端A处做一标记(如固定一个指针).在弹簧下端的挂钩上挂上钩码(每个钩码的质量都是50 g A=N/m.(结果取两位有效数字);此弹簧的弹力大小F弹跟弹簧伸长量∆x的关系是.(2)如果将指针固定在A点的下方P处,再作出x随F变化的图象,得出弹簧的劲度系数与k A相比,可能是( )AAA(3)如果将指针固定在A点的上方Q处,再作出x随F变化的图象,得出弹簧的劲度系数与k A相比,可能是( )AAA答案 (1)42(±2) F弹=42∆x 〔2〕B (3)A50 g,重力加速度g=9.8 m/s2.那么被测弹簧的劲度系数为N/m.答案 70“探究弹力和弹簧伸长量的关系〞的实验中,组成了如图实所示的装置,所用的每个钩码的质量都是30 g.他先测出不挂钩码时弹簧的自然长度,再将5个钩码逐个挂在弹簧的下端,每次都测出相应的弹簧总长度,将数据填在了下面的表中.(弹簧认为是轻弹簧,弹力始终未超出弹性限度,取g=10 m/s2)砝码质量〔g〕0 30 60 90 120 150 弹簧总长〔cm〕弹力大小〔N〕(1)试根据这些实验数据在以下列图实给定的坐标纸上作出弹簧所受弹力大小跟弹簧总长之间的函数关系的图线.(2)该图线跟横轴的交点表示的物理意义是.(3)该弹簧的劲度系数k是.答案 (1)(2)弹簧的原长 (3)25.9 N/m6.〔·模拟〕用纳米技术处理过的材料叫纳米材料,其性质与处理前相比会发生很多变化.如机械性能会成倍地增加,对光的反射能力会变得很低,熔点会大大地降低,甚至有特殊的磁性质.现有一纳米合金丝,欲测出其伸长量x与所受到的拉力F、长度L、截面直径D的关系.(1)测量上述物理量需要的主要器材是:、、等.(2)假设实验中测量的数据如下表,根据这些数据请写出x与F、L、D间的关系式:x=.(假设用到比例系数,可用k表示)长度(3)在研究并得到上述关系的过程中,主要运用的科学研究方法是(只需写出一种).(4)假设有一根合金丝的长度为20 cm,截面直径为0.200 mm,使用中要求其伸长量不能超过原长的百分之一,那么这根合金丝能承受的最大拉力为N.kFL答案 (1)弹簧测力计刻度尺螺旋测微器 (2)x=D。

实验二:探究弹力和弹簧伸长量的关系实验报告一、实验背景弹力,又称内弹力,是构成物体的物质间的内部相互作用。
当物体遭受外力的刺激时,在物体内部的分子及其成分之间会产生弹力,使物体返回到原来的形状,这样形成的弹力就是弹力。
弹力能够恢复物体原来的形状,是物体具有自保能力的根本原因[1]。
弹簧伸长量,也称为弹簧长度,是指装在被测物上的弹簧释放力时弹簧的伸长量,即弹簧从原来的状态(停机时的状态)变为被测物的形状,弹簧所增加的长度,以毫米为单位。
二、实验目的、实验材料、实验程序实验目的:探究普通小弹簧的弹力与伸长量的关系,为今后的科研提供参考依据。
实验材料:(1)弹簧1条;(2)勒耳器;(3)千分尺;实验程序:Step1:先用勒耳器将弹簧固定在实验架上;Step2:让弹簧从放松状态开始,将千分尺安装在弹簧上;Step3:弹簧被施加一定力时,记录下弹簧伸长量(以毫米为单位);Step4:记录应用力的大小(以牛顿为单位);Step5:重复上述步骤,并记录下弹簧的伸长量及力的大小;Step6:进行数据处理和数据分析,得出弹力与弹簧伸长量的关系。
三、实验数据及结果表1 力与弹簧伸长量的关系应用力/N 弹簧伸长量/mm0 01 0.54 2.05 2.56 3.07 3.59 4.5从上表可知,随着力的大小增加,弹簧伸长量也在增加,当力达到9牛时,弹簧伸长量达到了4.5mm。
从上图中可以看出,随着施加的力的增大,弹簧的伸长量呈正比增大,可以解释弹力大小与弹簧伸长量之间的正比例关系。
四、实验结论通过此次实验研究,可以得出结论:普通小弹簧的弹力与伸长量是成正比关系的,即随着施加的力的增大,弹簧的伸长量会呈正比增大。
让物体返回原来的形状,这样形成的弹力就是弹力,可以用正比例模型来描述它们之间的关系。
五、结论总结本次实验让我们了解到,弹力与弹簧伸长量是一个正比的关系,就是说,力的大小越大,弹簧的伸长量就越大,弹力也会越大。
本次实验为今后的科研提供了参考,也提升了我们实践能力。
探究弹力和弹簧伸长的关系【考纲知识梳理】一、实验目的探索弹力与弹簧伸长的定量关系,并学习其中的科学方法。
二、实验原理弹簧受到拉力会伸长,平衡时弹簧产生的弹力和外力大小相等。
这样弹力的大小可以通过测定外力而得出(可以用悬挂钩码的方法给弹簧施加拉力);弹簧的伸长可用直尺测出。
多测几组数据,用列表或作图的方法探索出弹力和弹簧伸长的定量关系。
三、实验器材轻弹簧、钩码(一盒)、刻度尺、铁架台、三角板、重垂线、坐标纸。
【要点精解】一、实验步骤1.将铁架台放于桌面上,将弹簧的一端固定于铁架台的横梁上,在靠近弹簧处将刻度尺固定于铁架台上,并用重垂线检查刻度尺是否垂直。
2.记下弹簧的原长(自然长度)l03.在弹簧下端挂上钩码,待钩码静止后,记下弹簧的的现长l及弹力F,算出伸长量x=l-l0,并改变钩码个数,多次测量。
数据记录表如下:数据记录:(弹簧原长l0= cm)4.根据测量数据画出F-x图像。
(以F为纵轴,以x为横轴)5.探索结论:按照F-x图中各点的分布与走向,尝试做出一条平滑的曲线(包括直线)。
所画的点不一定正好在这条曲线上,但要注意使曲线两侧的点数大致相同。
尝试写出曲线所代表的函数,首先尝试F-x是否为一次函数,如果不行则考虑二次函数……在实验误差范围内,应得出弹力的大小与弹簧的伸长量成正比,即F=kx,其中k的单位由F和x的单位决定。
讲课时应注意的几点:1.做实验时应提醒学生重视步骤2.描点时笔尖尽量细3.上课时要讲清楚刻度尺和三角板的用途和正确的使用方法4.逐差法的优点5.读数时调整刻度尺尽量读整数【例1】几个同学合作如图甲所示装置探究“弹力和弹簧伸长的关系”,弹簧的上端与标尺的零刻度对齐,他先读出不挂钩码时弹簧下端指针所指的标尺刻度,然后在弹簧下端挂上钩码,并逐个增加钩码,依次读出指针所指的标尺刻度,所得数据列表如下:(弹簧始终未超过弹性限度,重力加速度g=9.8m/s2)⑴根据所测数据,在图乙所示的坐标纸上作出弹簧指针所指的标尺刻度x与钩码质量m的关系曲线。
探究弹力和弹簧伸长的关系Company number:【WTUT-WT88Y-W8BBGB-BWYTT-19998】实验2:探究弹力和弹簧伸长的关系一、实验目的1.探究弹力和弹簧伸长之间的关系。
2.学会利用图象法处理实验数据。
二、实验原理1.下图所示,在弹簧下端悬挂钩码时弹簧会伸长,平衡时弹簧产生的弹力与所挂钩码的重力大小相等。
2.弹簧的长度可用刻度尺直接测出,伸长量可以由拉长后的长度减去弹簧原来的长度进行计算。
这样就可以研究弹簧的弹力和弹簧伸长量之间的定量关系了。
三、实验器材铁架台、弹簧、毫米刻度尺、钩码若干、三角板、坐标纸、重垂线、铅笔。
四、实验步骤1.下图所示,将铁架台放在桌面上(固定好),将弹簧的一端固定于铁架台的横梁上,让其自然下垂,在靠近弹簧处将刻度尺(分度值为 1 mm)固定于铁架台上,并用重垂线检查刻度尺是否竖直。
2.用刻度尺测出弹簧自然伸长状态时的长度l0,即原长。
3.如上图所示,在弹簧下端挂质量为m1的钩码,量出此时弹簧的长度l1,记录m1和l1,填入自己设计的表格中。
4.改变所挂钩码的质量,量出对应的弹簧长度,记录m2、m3、m4、m5和相应的弹簧长度l2、l3、l4、l5,并得出每次弹簧的伸长量x1、x2、x3、x4、x5。
钩码个数长度伸长量x 钩码质量m 弹力F0l0=1l1=x1=l1-l0m1=F1=2l2=x2=l2-l0m2=F2=3l3=x3=l3-l0m3=F3=1.以弹力F(大小等于所挂钩码的重力)为纵坐标,以弹簧的伸长量x为横坐标,用描点法作图。
连接各点,得出弹力F随弹簧伸长量x变化的图线。
2.以弹簧的伸长量为自变量,写出曲线所代表的函数。
首先尝试一次函数,如果不行则考虑二次函数。
3.得出弹力和弹簧伸长之间的定量关系,解释函数表达式中常数的物理意义。
六、误差分析1.本实验的误差来源之一是因弹簧拉力大小的不稳定造成的,因此,使弹簧的悬挂端固定,另一端通过悬挂钩码来充当对弹簧的拉力,可以提高实验的精确度。
实验二探究弹力和弹簧伸长的关系班级姓名座号1.在“探究弹力与弹簧伸长量的关系”中,关于操作步骤先后顺序,下列说法正确的()A.先测量弹簧的原长,后竖直悬挂B.先竖直悬挂,后测量弹簧的原长C.先后顺序对实验结果无影响D.先后顺序对实验结果的影响程度取决于弹簧的自身重量2.一个实验小组在“探究弹力和弹簧伸长量的关系”的实验中,使用两条不同的轻质弹簧a和b,得到弹力F与弹簧长度l的图象如图所示.下列表述正确的是()A.a的原长比b的长B.a的劲度系数比b的大C.a的劲度系数比b的小D.测得的弹力与弹簧的长度成正比3.某物理兴趣小组的同学在研究弹簧弹力的时候,测得弹力的大小F和弹簧长度L的关系如图所示,则由图线可知:(1)弹簧的劲度系数为_________。
(2)弹簧的弹力为5N时,弹簧的长度为__________。
4.如图甲所示,用铁架台、弹簧和多个已知质量且质量相等的钩码探究在弹性限度内弹簧弹力与弹簧伸长量的关系.(1)为完成实验,还需要的实验器材有:____________.(2)实验中需要测量的物理量有:________________.(3)图乙是弹簧弹力F与弹簧伸长量x的F-x图线,由此可求出弹簧的劲度系数为________N/m.图线不过原点的原因是由于___________________________________.(4)为完成该实验,设计的实验步骤如下:A.以弹簧伸长量为横坐标,以弹力为纵坐标,描出各组(x,F)对应的点,并用平滑的曲线连接起来;B.记下弹簧不挂钩码时其下端在刻度尺上的刻度l0;C.将铁架台固定于桌子上,并将弹簧一端系于横梁上,在弹簧附近竖直固定一把刻度尺;D.依次在弹簧下端挂上1个、2个、3个、4个…钩码,并分别记下钩码静止时弹簧下端所对应的刻度,并记录在表格内,然后取下钩码;E.以弹簧伸长量为自变量,写出弹力与弹簧伸长量的关系式.首先尝试写成一次函数,如果不行,则考虑二次函数;F.解释函数表达式中常数的物理意义;G.整理仪器.请将以上步骤按操作的先后顺序排列出来:________________________.5.为了探究弹力和弹簧伸长的关系,某同学选了甲、乙两根规格不同的弹簧进行测试,根据测得的数据绘出如图所示图象.(1)从图象上看,该同学没能完全按照实验要求做,从而使图象上端成为曲线,图象上端成为曲线是因为____________________________________.(2)这两根弹簧的劲度系数分别为________ N/m和________ N/m;若要制作一个精确程度较高的弹簧测力计,应选弹簧________(选填“甲”或“乙”).(3)从上述数据和图线中分析,请对这个研究课题提出一个有价值的建议.建议:________________________________________________________________. 6.用纳米技术处理过的材料叫纳米材料,其性质与处理前相比会发生很多变化,如机械性能会成倍地增加,对光的反射能力会变得非常低,熔点会大大降低,甚至有特殊的磁性质。
现有一种纳米合金丝,欲测定出其伸长量x与所受拉力F、长度L的关系。
(1)测量上述物理量需要的主要器材是____________、__________等。
(2)若实验中测量的数据如下表所示,根据这些数据请写出x与F、L间的关系式:x=_______。
(若用到比例系数,可用k表示。
假设实验中合金丝直径的变化可忽略)(3)在研究并得到上述关系的过程中,主要运用的科学研究方法是__________(只需写出一种)。
(4)若有一根由上述材料制成的粗细相同的合金丝的长度为20cm,使用中要求其伸长量不能超过原长的百分之一,那么这根合金丝能承受的最大拉力为________N。
7.(2016·台州模拟)某同学和你一起探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k。
做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上。
当弹簧自然下垂时,指针指示的刻度数值记作L0;弹簧下端挂一个50g的砝码时,指针指示的刻度数值记作L1;弹簧下端挂两个50g的砝码时,指针指示的刻度数值记作L2…挂七个50g的砝码时,指针指示的刻度数值记作L7。
(1)表中记录的是该同学已测出的6个值,其中有两个数值在记录时有误,它们的代表符号分别是________和________。
测量记录表:(2)实验中,L3和L7两个值还没有测定,请你根据图示将这两个测量值填入记录表中。
(3)为充分利用测量数据,该同学将所测得的数值按如下方法逐一求差,分别计算出了三个差值:d1=L4-L0=6.90cm,d2=L5-L1=6.90cm,d3=L6-L2=7.00cm。
请你给出第四个差值:d4=____________=____________cm。
(4)根据以上差值,可以求出每增加50g砝码的弹簧平均伸长量ΔL。
ΔL用d1、d2、d3、d4表示的式子为ΔL=____________,代入数据解得ΔL=______c(5)计算弹簧的劲度系数k=__________N/m。
(g取9.8m/s2)8.(2014·浙江·21)在“探究弹力和弹簧伸长量的关系”时,某同学把两弹簧如图连接起来进行探究(1)某次测量如图所示,指针示数为______cm.(2)在弹性限度内,将50 g的钩码逐个挂在弹簧下端,得到指针A、B的示数L A和L B如表所示.用表中数据计算弹簧Ⅰ的劲度系数为______N/m(重力加速度g=10 m/s2).由表中数据______(填“能”或“不能”)计算出弹簧Ⅱ的劲度系数.9.(2018·全国卷I ·T22) 如图甲,一弹簧上端固定在支架顶端,下端悬挂一托盘;一标尺由游标和主尺构成,主尺竖直固定在弹簧左边;托盘上方固定有一能与游标刻度线准确对齐的装置,简化为图中的指针。
现要测量图甲中弹簧的劲度系数。
当托盘内没有砝码时,移动游标,使其零刻度线对准指针,此时标尺读数为1.950cm;当托盘内放有质量为0.100 kg的砝码时,移动游标,再次使其零刻度线对准指针,标尺示数如图乙所示,其读数为cm。
当地的重力加速度大小为9.80 m/s2,此弹簧的劲度系数为N/m(保留3位有效数字)。
10.(2014·新课标Ⅱ·23)某实验小组探究弹簧的劲度系数k 与其长度(圈数)的关系.实验装置如图所示:一均匀长弹簧竖直悬挂,7个指针P 0、P 1、P 2、P 3、P 4、P 5、P 6分别固定在弹簧上距悬点0、10、20、30、40、50、60圈处;通过旁边竖直放置的刻度尺,可以读出指针的位置,P 0指向0刻度,设弹簧下端未挂重物时,各指针的位置记为x 0,挂有质量为0.100 kg 的砝码时,各指针的位置记为x .测量结果及部分计算结果如下表所示(n 为弹簧的圈数,取重力加速度为9.80 m/s 2),已知实验所用弹簧总圈数为60,整个弹簧的自由长度为11.88 cm.(1)将表中数据补充完整:①________,②________.(2)以n 为横坐标,1k 为纵坐标,在图10给出的坐标轴上画出1k-n 图象.图10(3)上图画出的直线可近似认为通过原点.若从实验中所用的弹簧截取圈数为n 的一段弹簧,该弹簧的劲度系数k 与其圈数n 的关系的表达式为k =________N/m.该弹簧的劲度系数k 与其自由长度l 0(单位为m )的关系的表达式为k =________N/m.实验二探究弹力和弹簧伸长的关系参考答案1.【解析】选B、D。
由于弹簧自身重量的影响,弹簧平放时的长度与竖直悬挂时的长度不同,竖直悬挂时长度更长一些。
由于实验时弹簧始终处于竖直状态,故弹簧长度一直受自重影响,所以测量原长时,应测量弹簧竖直悬挂时的长度,B、D项正确。
2.答案 B解析图象的横轴截距表示弹簧的原长,A错误;图象的斜率表示弹簧的劲度系数,B正确,C 错误;图象不过原点,D错误.3.【解析】由弹力的大小F和弹簧长度L的关系图可知,弹簧原长L0=10cm;弹簧形变量大小x=5cm 时,弹力F=10N,由胡克定律F=kx可得弹簧的劲度系数k=200N/m;弹簧的弹力为5N时,弹簧的形变量为x==2.5cm,当弹簧被压缩时,弹簧的长度为7.5cm,当弹簧被拉伸时,弹簧的长度为12.5cm。
答案:(1)200N/m(2)12.5 cm或7.5 cm4.答案(1)刻度尺(2)弹簧原长、弹簧挂不同个数的钩码时所对应的伸长量(或对应的弹簧长度)(3)200弹簧自身存在重力(4)CBDAEFG解析(1)根据实验原理可知还需要刻度尺来测量弹簧原长和形变量;(2)根据实验原理,实验中需要测量的物理量有弹簧的原长、弹簧挂不同个数的钩码时所对应的伸长量(或对应的弹簧长度);(3)取图象中(0.5,0)和(3.5,6)两个点,代入F=kx可得k=200 N/m,由于弹簧自身存在重力,使得弹簧不加外力时就有形变量;(4)根据完成实验的合理性可知先后顺序为CBDAEFG.5.答案(1)形变量超过弹簧的弹性限度(2)66.7200甲(3)见解析解析(1)在弹性限度内弹簧的弹力与形变量成正比,超过弹簧的弹性限度,则此规律不成立,所以所给的图象上端成为曲线,是因为形变量超过弹簧的弹性限度.(2)甲、乙两根弹簧的劲度系数分别为:k甲=F甲Δx甲=46×10-2N/m≈66.7 N/m,k乙=F乙Δx乙=84×10-2N/m=200 N/m.要制作一个精确程度较高的弹簧测力计,应选用一定的外力作用时形变量大的弹簧,故选弹簧甲.(3)建议:实验中钩码不能挂太多,以保证弹簧的形变量在弹性限度内.6.【解析】(1)用弹簧测力计测量力的大小,用刻度尺测量长度。
(2)由题目所给的数据分析可知:当力一定时,伸长量与长度成正比;当长度一定时,伸长量和力成正比,故x=kFL(取一组数据验证,式中的k不为零)。
(3)研究伸长量与拉力、长度的关系时,可以先控制某一个量不变,如长度不变,再研究伸长量与拉力的关系,这种方法称为控制变量法。
这是物理实验中的一个重要研究方法。
(4)代入表中数据把式中的k求出,得k=0.0008N-1,再代入已知数据,L=20cm,x==0.2cm,可求得最大拉力F=12.5N 。
答案:(1)弹簧测力计 刻度尺 (2)kFL (3)控制变量法 (4)12.57.【解析】(1)通过对6个值的分析比较可知记录有误的是L 5、L 6。
(2)用最小刻度是毫米的刻度尺测量时,正确读数并记录到毫米的下一位,即L 3=6.85cm ,L 7=14.05cm 。