【金版教程】2016秋高一人教版数学必修一练习：第三章 单元质量测评1 Word版含解析

新版高一数学必修第一册第三章全部配套练习题（含答案和解析）3.1.1 函数的概念基 础 练巩固新知 夯实基础1．下列说法正确的是( )A ．函数值域中每一个数在定义域中一定只有一个数与之对应B ．函数的定义域和值域可以是空集C ．函数的定义域和值域一定是数集D ．函数的定义域和值域确定后，函数的对应关系也就确定了2．若函数y ＝f (x )的定义域M ＝{x |－2≤x ≤2}，值域为N ＝{y |0≤y ≤2}，则函数y ＝f (x )的图象可能是( )3．函数f (x )＝x －1x －2的定义域为( ) A ．[1,2)∪(2，＋∞) B ．(1，＋∞) C ．[1,2)D ．[1，＋∞)4．已知函数f (x )的定义域为[－1,2)，则函数f (x －1)的定义域为( )A ．[－1,2)B ．[0,2)C ．[0,3)D ．[－2,1)5．函数y ＝5x ＋4x －1的值域是( )A ．(－∞，5)B ．(5，＋∞)C ．(－∞，5)∪(5，＋∞)D ．(－∞，1)∪(1，＋∞) 6．函数y ＝x ＋1的值域为( )A ．[－1，＋∞)B ．[0，＋∞)C ．(－∞，0]D ．(－∞，－1]7．已知函数f (x )＝x ＋1x，则f (2)＋f (－2)的值是( )A ．－1B ．0C ．1D ．2 8．下列函数完全相同的是( )A ．f (x )＝|x |，g (x )＝(x )2B ．f (x )＝|x |，g (x )＝x 2C ．f (x )＝|x |，g (x )＝x 2x D ．f (x )＝x 2－9x －3，g (x )＝x ＋39．求下列函数的定义域：(1)f (x )＝1x ＋1； (2)y ＝x 2－1＋1－x 2； (3)y ＝2x ＋3； (4)y ＝x ＋1x 2－1.10．求下列函数的值域：(1)y ＝2x ＋1，x ∪{1,2,3,4,5}； (2)y ＝x 2－4x ＋6，x ∪[1,5)； (3)y ＝3－5x x －2； (4)y ＝x －x ＋1.能 力 练综合应用 核心素养11．已知等腰∪ABC 的周长为10，则底边长y 关于腰长x 的函数关系为y ＝10－2x ，此函数的定义域为( )A ．RB ．{x |x >0}C ．{x |0<x <5}D.⎩⎨⎧x ⎪⎪⎭⎬⎫52<x <5 12．函数f (x )＝1x 2＋1(x ∪R )的值域是( )A ．(0,1)B ．(0,1]C ．[0,1)D ．[0,1]13．函数y ＝f (x )的图象与直线x ＝a 的交点个数有( )A ．必有一个B ．一个或两个C ．至多一个D ．可能两个以上 14．函数y ＝3－2x －x 2＋14－x 2的定义域为____________________(用区间表示)．15．函数y ＝1x －2的定义域是A ，函数y ＝x 2＋2x －3的值域是B ，则A ∩B ＝________________(用区间表示)．16．若函数f (2x －1)的定义域为[0,1)，则函数f (1－3x )的定义域为________． 17．若函数y ＝ax 2＋2ax ＋3的值域为[0，＋∞)，则a 的取值范围是________． 18．已知函数f (x )＝x 21＋x 2.(1)求f (2)＋f ⎝⎛⎭⎫12，f (3)＋f ⎝⎛⎭⎫13的值． (2)求证：f (x )＋f ⎝⎛⎭⎫1x 是定值．(3)求f (2)＋f ⎝⎛⎭⎫12＋f (3)＋f ⎝⎛⎭⎫13＋…＋f (2019)＋f ⎝⎛⎭⎫12019的值．19．已知函数y ＝mx 2－6mx ＋m ＋8的定义域是R ，求实数m 的取值范围．20.已知函数f (x )＝3－x ＋1x ＋2的定义域为集合A ，B ＝{x |x <a }． (1)求集合A ；(2)若A ∪B ，求a 的取值范围；(3)若全集U ＝{x |x ≤4}，a ＝－1，求∪U A 及A ∩(∪U B )．【参考答案】1. C 解析 根据从集合A 到集合B 函数的定义可知，强调A 中元素的任意性和B 中对应元素的唯一性，所以A 中的多个元素可以对应B 中的同一个元素，从而选项A 错误；同样由函数定义可知，A 、B 集合都是非空数集，故选项B 错误；选项C 正确；对于选项D ，可以举例说明，如定义域、值域均为A ＝{0,1}的函数，对应关系可以是x →x ，x ∪A ，可以是x →x ，x ∪A ，还可以是x →x 2，x ∪A .2. B 解析 A 中定义域是{x |－2≤x ≤0}，不是M ＝{x |－2≤x ≤2}，C 中图象不表示函数关系，D 中值域不是N ＝{y |0≤y ≤2}．3. A 解析 由题意知，要使函数有意义，需满足⎩⎪⎨⎪⎧x －1≥0，x －2≠0即x ≥1且x ≠2.4. C 解析 ∪f (x )的定义域为[－1,2)，∪－1≤x －1<2，得0≤x <3，∪f (x －1)的定义域为[0,3)．5. C 解析 ∪y ＝5x ＋4x －1＝5(x －1)＋9x －1＝5＋9x －1，且9x －1≠0，∪y ≠5，即函数的值域为(－∞，5)∪(5，＋∞)．6. B 解析 由于x ＋1≥0，所以函数y ＝x ＋1的值域为[0，＋∞)．7. B 解析 f (2)＋f (－2)＝2＋12－2－12＝0.8. B 解析 A 、C 、D 的定义域均不同．9. 解 (1)要使函数有意义，即分式有意义，则x ＋1≠0，x ≠－1.故函数的定义域为{x |x ≠－1}．(2)要使函数有意义，则⎩⎪⎨⎪⎧ x 2－1≥0，1－x 2≥0，即⎩⎪⎨⎪⎧x 2≥1，x 2≤1.所以x 2＝1，从而函数的定义域为{x |x ＝±1}＝{1，－1}． (3)函数y ＝2x ＋3的定义域为{x |x ∪R }．(4)因为当x 2－1≠0，即x ≠±1时，x ＋1x 2－1有意义，所以原函数的定义域是{x |x ≠±1，x ∪R }．10. 解 (1)∪x ∪{1,2,3,4,5}，∪(2x ＋1)∪{3,5,7,9,11}，即所求函数的值域为{3,5,7,9,11}．(2)y ＝x 2－4x ＋6＝(x －2)2＋2. ∪x ∪[1,5)，∪其图象如图所示， 当x ＝2时，y ＝2；当x ＝5时，y ＝11. ∪所求函数的值域为[2,11)．(3)函数的定义域为{x |x ≠1}，y ＝3－5x x －2＝－5(x －2)＋7x －2＝－5－7x －2，所以函数的值域为{y |y ≠－5}．(4)要使函数式有意义，需x ＋1≥0，即x ≥－1，故函数的定义域为{x |x ≥－1}．设t ＝x ＋1，则x ＝t 2－1(t ≥0)，于是y ＝t 2－1－t ＝⎝⎛⎭⎫t －122－54，又t ≥0，故y ≥－54，所以函数的值域为{y |y ≥－54}． 11. D 解析 ∪ABC 的底边长显然大于0，即y ＝10－2x >0，∪x <5，又两边之和大于第三边，∪2x >10－2x ，x >52，∪此函数的定义域为⎩⎨⎧x ⎪⎪⎭⎬⎫52<x <5.12. B 解析 由于x ∪R ，所以x 2＋1≥1,0<1x 2＋1≤1，即0<y ≤1.13. C 解析 当a 在f (x )定义域内时，有一个交点，否则无交点．14. [－1,2)∪(2,3] 解析 使根式3－2x －x 2有意义的实数x 的集合是{x |3－2x －x 2≥0}即{x |(3－x )(x ＋1)≥0}＝{x |－1≤x ≤3}，使分式14－x 2有意义的实数x 的集合是{x |x ≠±2}，所以函数y ＝3－2x －x 2＋14－x 2的定义域是{x |－1≤x ≤3}∩{x |x ≠±2}＝{x |－1≤x ≤3，且x ≠2}．15. [0,2)∪(2，＋∞) 解析 要使函数式y ＝1x －2有意义，只需x ≠2，即A ＝{x |x ≠2}；函数y ＝x 2＋2x －3＝(x ＋1)2－4≥0，即B ＝{y |y ≥0}，则A ∩B ＝{x |0≤x <2或x >2}．16. ⎝⎛⎦⎤0，23 解 因为f (2x －1)的定义域为[0,1)，即0≤x <1，所以－1≤2x －1<1.所以f (x )的定义域为[－1,1)．所以－1≤1－3x <1，解得0<x ≤23.所以f (1－3x )的定义域为⎝⎛⎦⎤0，23. 17. [3，＋∞) 解析 函数y ＝ax 2＋2ax ＋3的值域为[0，＋∞)，则函数f (x )＝ax 2＋2ax ＋3的值域要包括0，即最小值要小于等于0.则{ a >0，Δ＝4a 2－12a ≥0，解得a ≥3.所以a 的取值范围是[3，＋∞)．18. 解 (1)因为f (x )＝x 21＋x 2，所以f (2)＋f ⎝⎛⎭⎫12＝221＋22＋⎝⎛⎭⎫1221＋⎝⎛⎭⎫122＝1，f (3)＋f ⎝⎛⎭⎫13＝321＋32＋⎝⎛⎭⎫1321＋⎝⎛⎭⎫132＝1. (2)证明：f (x )＋f ⎝⎛⎭⎫1x ＝x 21＋x 2＋⎝⎛⎭⎫1x 21＋⎝⎛⎭⎫1x 2＝x 21＋x 2＋1x 2＋1＝x 2＋1x 2＋1＝1. (3)由(2)知f (x )＋f ⎝⎛⎭⎫1x ＝1，所以f (2)＋f ⎝⎛⎭⎫12＝1，f (3)＋f ⎝⎛⎭⎫13＝1，f (4)＋f ⎝⎛⎭⎫14＝1，…，f (2019)＋f ⎝⎛⎭⎫12019＝1. 所以f (2)＋f ⎝⎛⎭⎫12＋f (3)＋f ⎝⎛⎭⎫13＋…＋f (2019)＋f ⎝⎛⎭⎫12019＝2018. 19. 解 ∪当m ＝0时，y ＝8，其定义域是R .∪当m ≠0时，由定义域为R 可知，mx 2－6mx ＋m ＋8≥0对一切实数x 均成立，于是有⎩⎪⎨⎪⎧m >0，Δ＝(－6m )2－4m (m ＋8)≤0，解得0<m ≤1.由∪∪可知，m ∪[0,1]． 20. 解 (1)使3－x 有意义的实数x 的集合是{x |x ≤3}，使1x ＋2有意义的实数x 的集合是{x |x >－2}． 所以，这个函数的定义域是{x |x ≤3}∩{x |x >－2}＝{x |－2<x ≤3}．即A ＝{x |－2<x ≤3}． (2)因为A ＝{x |－2<x ≤3}，B ＝{x |x <a }且A ∪B ，所以a >3.(3)因为U ＝{x |x ≤4}，A ＝{x |－2<x ≤3}，所以∪U A ＝(－∞，－2]∪(3,4]． 因为a ＝－1，所以B ＝{x |x <－1}，所以∪U B ＝[－1,4]，所以A ∩∪U B ＝[－1,3]．3.1.2 函数的表示法基 础 练巩固新知 夯实基础1.小明骑车上学，开始时匀速行驶，途中因交通堵塞停留了一段时间后，为了赶时间加快速行驶．与以上事件吻合得最好的图象是( )2．已知f (x )是一次函数，2f (2)－3f (1)＝5,2f (0)－f (－1)＝1，则f (x )＝( )A ．3x ＋2B ．3x －2C ．2x ＋3D ．2x －33.已知函数f (x )＝⎩⎪⎨⎪⎧x ＋1，x ∪[－1，0]，x 2＋1，x ∪0，1]，则函数f (x )的图象是( )4.已知函数y ＝f (x )的对应关系如下表，函数y ＝g (x )的图象是如图的曲线ABC ，其中A (1,3)，B (2,1)，C (3,2)，则f [g (2)]的值为( )A ．3B ．2C ．1D ．0 5.函数f (x )＝⎩⎪⎨⎪⎧2x 2，0≤x ≤1，2，1<x <2，3，x ≥2的值域是( )A.RB.[0，＋∞)C.[0,3]D.{x |0≤x ≤2或x ＝3} 6.设f (x )＝⎩⎪⎨⎪⎧x ＋1，x >0，1，x ＝0，－1，x <0，则f (f (0))等于( )A.1B.0C.2D.－17．已知f (2x ＋1)＝3x －2且f (a )＝4，则a 的值为________．8．已知f (x )是一次函数，且满足3f (x ＋1)－2f (x －1)＝2x ＋17，求f (x )的解析式．9．已知二次函数f (x )满足f (0)＝0，且对任意x ∪R 总有f (x ＋1)＝f (x )＋x ＋1，求f (x )．10 (1)已知f (x ＋1x )＝x 2＋1x2，求f (x )的解析式．(2)已知f (x )满足2f (x )＋f (1x )＝3x ，求f (x )的解析式．(3)已知f (x )＋2f (－x )＝x 2＋2x ，求f (x )的解析式．能 力 练综合应用 核心素养11．如果f ⎝⎛⎭⎫1x ＝x1－x ，则当x ≠0,1时，f (x )等于( )A.1xB.1x －1C.11－xD.1x－1 12．已知x ≠0时，函数f (x )满足f (x －1x )＝x 2＋1x 2，则f (x )的表达式为( )A ．f (x )＝x ＋1x (x ≠0) B ．f (x )＝x 2＋2(x ≠0)C ．f (x )＝x 2(x ≠0)D ．f (x )＝(x －1x)2(x ≠0)13.已知函数y ＝⎩⎪⎨⎪⎧x 2＋1，x ≤0，－2x ，x >0，则使函数值为5的x 的值是( )A.－2或2B.2或－52C.－2D.2或－2或－5214.若f (x )是一次函数，2f (2)－3f (1)＝5,2f (0)－f (－1)＝1，则f (x )＝( )A ．3x ＋2B ．3x －2C ．2x ＋3D ．2x －3 15．已知f (x －1)＝x 2，则f (x )的解析式为( )A ．f (x )＝x 2＋2x ＋1B ．f (x )＝x 2－2x ＋1C ．f (x )＝x 2＋2x －1D ．f (x )＝x 2－2x －116.已知f (n )＝⎩⎪⎨⎪⎧n －3，n ≥10，f f n ＋5，n <10，则f (8)＝________.17．已知函数y ＝f (x )满足f (x )＝2f (1x )＋x ，则f (x )的解析式为____________．18. 已知函数f (x )＝1＋|x |－x2(－2<x ≤2).(1)用分段函数的形式表示该函数； (2)画出该函数的图象； (3)写出该函数的值域.19．设f (x )是R 上的函数，且满足f (0)＝1，并且对任意实数x ，y ，有f (x －y )＝f (x )－y (2x －y ＋1)，求f (x )的解析式．【参考答案】1. C 解析 先分析小明的运动规律，再结合图象作出判断．距学校的距离应逐渐减小，由于小明先是匀速运动，故前段是直线段，途中停留时距离不变，后段加速，直线段比前段下降的快，故应选C.2. B 解析 设f (x )＝kx ＋b (k ≠0)，∪2f (2)－3f (1)＝5,2f (0)－f (－1)＝1，∪⎩⎪⎨⎪⎧ k －b ＝5k ＋b ＝1，∪⎩⎪⎨⎪⎧k ＝3b ＝－2，∪f (x )＝3x －2. 3. A 解析 当x ＝－1时，y ＝0，排除D ；当x ＝0时，y ＝1，排除C ；当x ＝1时，y ＝2，排除B. 4. B 解析 由函数g (x )的图象知，g (2)＝1，则f [g (2)]＝f (1)＝2.5. D 解析 当0≤x ≤1时，f (x )∪[0,2]，当1<x <2时，f (x )＝2，当x ≥2时，f (x )＝3， ∪值域是{x |0≤x ≤2或x ＝3}.6. C7. 5 解析 ∪f (2x ＋1)＝3x －2＝32(2x ＋1)－72，∪f (x )＝32x －72，∪f (a )＝4，即32a －72＝4，∪a ＝5.8. 解 设f (x )＝ax ＋b (a ≠0)，则3f (x ＋1)－2f (x －1)＝3ax ＋3a ＋3b －2ax ＋2a －2b ＝ax ＋5a ＋b ，即ax ＋5a ＋b ＝2x ＋17不论x 为何值都成立，∪⎩⎪⎨⎪⎧ a ＝2，b ＋5a ＝17，解得⎩⎪⎨⎪⎧a ＝2，b ＝7，∪f (x )＝2x ＋7. 9. 解 设f (x )＝ax 2＋bx ＋c (a ≠0)，∪f (0)＝c ＝0，∪f (x ＋1)＝a (x ＋1)2＋b (x ＋1)＋c ＝ax 2＋(2a ＋b )x ＋a ＋b ， f (x )＋x ＋1＝ax 2＋bx ＋x ＋1＝ax 2＋(b ＋1)x ＋1.∪⎩⎪⎨⎪⎧2a ＋b ＝b ＋1，a ＋b ＝1. ∪⎩⎨⎧a ＝12，b ＝12.∪f (x )＝12x 2＋12x .10. 解 (1)∪f (x ＋1x )＝x 2＋1x 2＝(x ＋1x )2－2，且x ＋1x ≥2或x ＋1x ≤－2,∪f (x )＝x 2－2(x ≥2或x ≤－2)．(2)∪2f (x )＋f (1x )＝3x ，∪把∪中的x 换成1x ，得2f (1x )＋f (x )＝3x .∪, ∪×2－∪得3f (x )＝6x －3x ，∪f (x )＝2x －1x (x ≠0)．(3)以－x 代x 得：f (－x )＋2f (x )＝x 2－2x .与f (x )＋2f (－x )＝x 2＋2x 联立得：f (x )＝13x 2－2x .11. B 解析 令1x ＝t ，则x ＝1t ，代入f ⎝⎛⎭⎫1x ＝x 1－x ，则有f (t )＝1t1－1t ＝1t －1，故选B. 12. B 解析 ∪f (x －1x )＝x 2＋1x 2＝(x －1x)2＋2，∪f (x )＝x 2＋2(x ≠0)．13. C14. B 解析 设f (x )＝ax ＋b ，由题设有⎩⎪⎨⎪⎧ 2(2a ＋b )－3(a ＋b )＝5，2(0·a ＋b )－(－a ＋b )＝1.解得⎩⎪⎨⎪⎧a ＝3，b ＝－2.所以选B.15. A 解析 令x －1＝t ，则x ＝t ＋1，∪f (t )＝f (x －1)＝(t ＋1)2＝t 2＋2t ＋1，∪f (x )＝x 2＋2x ＋1.16. 7 解析 因为8<10，所以代入f (n )＝f (f (n ＋5))，即f (8)＝f (f (13))；因为13>10，所以代入f (n )＝n －3，得f (13)＝10，故得f (8)＝f (10)＝10－3＝7.17. f (x )＝－x 2＋23x (x ≠0) 解析 ∪f (x )＝2f (1x )＋x ，∪∪将x 换成1x ，得f (1x )＝2f (x )＋1x .∪由∪∪消去f (1x )，得f (x )＝－23x －x3，即f (x )＝－x 2＋23x(x ≠0)．18.解 (1)∪当0≤x ≤2时，f (x )＝1＋x －x 2＝1；∪当－2<x <0时，f (x )＝1＋－x －x2＝1－x .所以f (x )＝⎩⎪⎨⎪⎧1，0≤x ≤2，1－x ，－2<x <0.(2)函数f (x )的图象如图所示.(3)由函数f (x )的图象知，f (x )在(－2,2]上的值域为[1,3).19 .解 因为对任意实数x ，y ，有f (x －y )＝f (x )－y (2x －y ＋1)，所以令y ＝x ，有f (0)＝f (x )－x (2x －x ＋1)，即f (0)＝f (x )－x (x ＋1)． 又f (0)＝1，∪f (x )＝x (x ＋1)＋1＝x 2＋x ＋1.3.2.1 第1课时 函数的单调性基 础 练巩固新知 夯实基础1．函数f (x )的定义域为(a ，b )，且对其内任意实数x 1，x 2均有(x 1－x 2)(f (x 1)－f (x 2))<0，则f (x )在(a ，b )上( ) A ．增函数B ．减函数C ．不增不减函数D ．既增又减函数2．若函数f (x )在区间(a ，b )上是增函数，在区间(b ，c )上也是增函数，则函数f (x )在区间(a ，b )∪(b ，c )上( )A ．必是增函数B ．必是减函数C ．是增函数或减函数D ．无法确定单调性3．如果函数f (x )在[a ，b ]上是增函数，那么对于任意的x 1，x 2∪[a ，b ](x 1≠x 2)，下列结论中不正确的是( ) A.f x 1－f x 2x 1－x 2>0B ．(x 1－x 2)[f (x 1)－f (x 2)]>0C ．若x 1<x 2，则f (a )<f (x 1)<f (x 2)<f (b ) D.x 1－x 2f x 1－f x 2>0 4．对于函数y ＝f (x )，在给定区间上有两个数x 1，x 2，且x 1<x 2，使f (x 1)<f (x 2)成立，则y ＝f (x )( )A ．一定是增函数B ．一定是减函数C ．可能是常数函数D ．单调性不能确定5．下列函数中，在(－∞，0]内为增函数的是( ) A ．y ＝x 2－2 B ．y ＝3xC ．y ＝1＋2xD ．y ＝－(x ＋2)26．已知函数f (x )＝x 2＋bx ＋c 的图象的对称轴为直线x ＝1，则( )A ．f (－1)<f (1)<f (2)B ．f (1)<f (2)<f (－1)C ．f (2)<f (－1)<f (1)D ．f (1)<f (－1)<f (2)7．若函数f (x )＝2x 2－mx ＋3，当x ∪[－2，＋∞)时是增函数，当x ∪(－∞，－2)时是减函数，则f (1)＝________.8．已知函数f (x )＝⎩⎪⎨⎪⎧(a －3)x ＋5，x ≤1，2a x ，x >1是R 上的减函数，则实数a 的取值范围是 。

第二章 单元质量测评(一)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，满分150分，考试时间120分钟．第Ⅰ卷 (选择题，共60分)一、选择题(本大题共12小题，每小题5分，共60分)1．已知集合M ＝{－1,1}，N ＝⎩⎨⎧⎭⎬⎫x | 12<2x ＋1<4，x ∈Z ，则M ∩N 为( )A ．{－1,1}B ．{－1}C ．{0}D ．{－1,0} 答案 B解析 ∵12<2x ＋1<4，∴－1<x ＋1<2，∴－2<x <1.又x ∈Z ，∴N ＝{－1,0}，∴M ∩N ＝{－1}．2．[2016·福建厦门一中月考]幂函数f (x )的图象过点(2，m )且f (m )＝16，则实数m 的值为( )A ．4或12B ．2或－2C ．4或14D .14或2 答案 C解析 设幂函数f (x )＝x a ，由图象过点(2，m )，得f (2)＝2a ＝m ，所以f (m )＝m a＝2a 2＝16，解得a ＝－2或2，所以m ＝22＝4或m ＝2－2＝14，故选C.3．[2015·湖南师大附中高一考试]函数y ＝xlg (2－x )的定义域是( )A ．[0,2)B ．[0,1)∪(1,2)C ．(1,2)D ．[0,1) 答案 B解析 若使函数有意义，则⎩⎪⎨⎪⎧x ≥0，2－x >02－x ≠1，解得0≤x <2且x ≠1.选B.4.⎝⎛⎭⎪⎪⎫36a 94⎝ ⎛⎭⎪⎪⎫63a 94等于( ) A ．a 16 B ．a 8 C ．a 4 D ．a 2 答案 C 解析原式＝⎩⎨⎧⎭⎬⎫⎣⎢⎢⎡⎦⎥⎥⎤(a 9)16 13 4·⎩⎨⎧⎭⎬⎫⎣⎢⎢⎡⎦⎥⎥⎤(a 9)13 16 4＝a ·a＝a 2·a 2＝a 4，所以答案选C.5．已知函数f (x )＝log a (x ＋b )的图象如右图所示，则f (6)的值为( )A ．3B ．6C ．5D ．4 答案 D解析 把(－2,0)和(0,2)代入y ＝log a (x ＋b )得：⎩⎪⎨⎪⎧ 0＝log a (－2＋b )，2＝log ab ，∴⎩⎪⎨⎪⎧a ＝3，b ＝3，∴f (6)＝log3(6＋3)＝4.6．[2016·哈三中高一月考]设a ＝log 312，b ＝30.2，c ＝⎝ ⎛⎭⎪⎫120.3，则a ，b ，c 的大小关系是( )A ．a <b <cB ．a <c <bC ．b <a <cD ．c <b <a答案 B解析 ∵a <0，b >1，c ∈(0,1)，∴a <c <b ，选B.7．已知f (x )是偶函数，它在[0，＋∞)上是减函数，若f (lg x )>f (1)，则x 的取值范围是( )A.110<x <1B ．0<x <110或x >1 C.110<x <10 D ．0<x <1或x >10 答案 C解析 ∵f (x )为偶函数，且f (x )在[0，＋∞)上是减函数，∴f (x )在(－∞，0)上是增函数．由函数的对称性且f (lg x )>f (1)，∴－1<lg x <1.∴110<x <10.8．[2015·玉溪一中月考]已知a ＝log 32，那么log 38－2log 36用a 表示是( )A ．5a －2B ．a －2C ．3a －(1＋a )2D ．3a －a 2－1答案 B解析 log 38－2log 36＝log 323－2log 3(2×3)＝3log 32－2(log 32＋log 33)＝log 32－2＝a －2，所以答案选B.9．函数y ＝a x－1a (a >0，a ≠1)的图象可能是( )答案 D解析 当a >1时，函数y ＝a x 单调递增，0<1a <1，函数y ＝a x －1a (a >0，a ≠1)的图象由y ＝a x的图象向下平移1a 个单位长度得到，故A ，B 不正确；当0<a <1时，y ＝a x 单调递减，1a >1，函数y ＝a x －1a (a >0，a ≠1)的图象由y ＝a x的图象向下平移1a 个单位长度得到，故C 不正确，故选D.10．[2015·邯郸高一质检]已知函数f (x )＝|log 2x |，正实数m ，n 满足m <n ，且f (m )＝f (n )，若f (x )在区间[m 2，n ]上的最大值为2，则m 、n 的值分别为( )A.12，2B.14，2C.22， 2D.14，4 答案 A解析 f (x )的图象如图所示：∵m <n ，f (m )＝f (n )， ∴0<m <1<n . ∴m 2<m <1.又∵f (x )在(0,1)上递减， ∴f (m 2)＝|log 2m 2|＝2， 解得m ＝12.∴f (n )＝f (m )＝|log 2n |＝⎪⎪⎪⎪⎪⎪log 212＝1，解得n ＝2，选A.11．[2016·清华附中期中考试]设集合S ＝{y |y ＝3x ，x ∈R }，T ＝{(x ，y )|y ＝x 2－1，x ∈R }，则S ∩T 是( )A ．(0，＋∞)B ．(－1，＋∞)C ．∅D ．R 答案 C解析 集合S 是指数函数y ＝3x 的值域，而集合T 表示函数y ＝x 2－1图象上的点的集合，两个集合中的元素不相同，所以交集是空集，故选C.12．[2015·湖北荆州中学期中]下列函数图象关于原点对称的有( )①f (x )＝x －1＋1－x ；②f (x )＝log 2(x ＋x 2＋1)；③f (x )＝1x ，x∈(－1,0)∪(0,1]；④f (x )＝－x lg |x |.A ．①②B ．①③C ．②③D ．②④ 答案 D解析 函数①的定义域为{1}，值域为{0}，所以函数图象只有一个点(1,0)，不关于原点对称；函数②定义域为R ，且函数f (x )为奇函数，所以其图象关于原点对称；函数③的定义域为(－1,0)∪(0,1]不关于原点对称；函数④的定义域为{x |x ≠0}，且函数f (x )为奇函数，所以其图象关于原点对称，所以正确答案为D.第Ⅱ卷 (非选择题，共90分)二、填空题(本大题共4小题，每小题5分，共20分)13．已知函数y ＝log a (x －3)－1的图象恒过定点P ，则点P 的坐标是________．答案 (4，－1)解析 y ＝log a x 的图象恒过点(1,0)，令x －3＝1，则x ＝4； 令y ＋1＝0，则y ＝－1.14．已知函数f (x )＝⎩⎪⎨⎪⎧3x ＋1，x ≤0，log 2x ，x >0，则使函数f (x )的图象位于直线y ＝1上方的x 的取值范围是________．答案 {x |－1<x ≤0或x >2}解析 当x ≤0时，3x ＋1>1⇒x ＋1>0，∴－1<x ≤0； 当x >0时，log 2x >1⇒x >2，∴x >2.综上所述，x 的取值范围为－1<x ≤0或x >2.15．函数f (x )＝⎝ ⎛⎭⎪⎫23x 2－2x的单调递减区间是________．答案 [1，＋∞)解析 令u ＝x 2－2x ，其递增区间为[1，＋∞)，根据函数y ＝⎝ ⎛⎭⎪⎫23u是定义域上的减函数知，函数f (x )的减区间就是[1，＋∞)．16．[2015·江苏盐城中学高一期中]函数y ＝2x－log 12(x ＋1)在区间[0,1]上的最大值和最小值之和为________．答案 4解析 因为y ＝2x 在[0,1]上单调递增，y ＝log 12 (x ＋1)在[0,1]上单调递减，所以y ＝f (x )＝2x －log 12 (x ＋1)在[0,1]单调递增，所以y 的最大值为f (1)＝21－log 12 2＝2－(－1)＝3，最小值为f (0)＝20－log 12 1＝1－0＝1，所以最大值和最小值之和为4.三、解答题(本大题共6小题，满分70分)17．(本小题满分10分)已知函数f (x )＝x m －2x 且f (4)＝72. (1)求m 的值； (2)判定f (x )的奇偶性；(3)判断f (x )在(0，＋∞)上的单调性，并给予证明． 解 (1)因为f (4)＝72，所以4m －24＝72，所以m ＝1. (2)由(1)知f (x )＝x －2x ， 因为f (x )的定义域为{x |x ≠0}，又f (－x )＝－x －2－x ＝－⎝ ⎛⎭⎪⎫x －2x ＝－f (x )，所以f (x )是奇函数．(3)f (x )在(0，＋∞)上单调递增． 设x 1>x 2>0，则f (x 1)－f (x 2)＝x 1－2x 1－⎝ ⎛⎭⎪⎫x 2－2x 2＝(x 1－x 2)⎝ ⎛⎭⎪⎫1＋2x 1x 2， 因为x 1>x 2>0，所以x 1－x 2>0,1＋2x 1x 2>0，所以f (x 1)>f (x 2)．所以f (x )在(0，＋∞)上为单调递增函数．18．[2016·浙江学军中学期中](本小题满分12分)已知f (x )＝9x －2×3x ＋4，x ∈[－1,2]，求f (x )的最大值与最小值．解 令t ＝3x，∵x ∈[－1,2]，∴t ∈⎣⎢⎡⎦⎥⎤13，9， 原式变为y ＝t 2－2t ＋4＝(t －1)2＋3.∵t ∈⎣⎢⎡⎦⎥⎤13，9，∴当t ＝1时，此时x ＝0，f (x )min ＝3；当t ＝9时，此时x ＝2，f (x )max ＝67. ∴f (x )的最大值为67，最小值为3.19．[2016·安徽蚌埠二中期末](本小题满分12分)设y 1＝log a (3x ＋1)，y 2＝log a (－3x )，其中0<a <1.(1)若y 1＝y 2，求x 的值； (2)若y 1>y 2，求x 的取值范围．解 (1)∵y 1＝y 2，∴log a (3x ＋1)＝log a (－3x )， ∴3x ＋1＝－3x ，解得x ＝－16，经检验x ＝－16在函数的定义域内，∴x ＝－16. (2)y 1>y 2，即log a (3x ＋1)>log a (－3x )(0<a <1)， ∴⎩⎪⎨⎪⎧3x ＋1>0－3x >03x ＋1<－3x，解得－13<x <－16，∴x 的取值范围为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪－13<x <－16.20．(本小题满分12分)设a >0，f (x )＝e x a ＋ae x 在R 上是偶函数． (1)求a 的值；(2)证明：f (x )在(0，＋∞)上是增函数．解 (1)∵f (x )在R 上是偶函数，∴f (x )＝f (－x )(x ∈R )．∴e x a ＋ae x ＝e －x a ＋a e －.∴e x a ＋a e x ＝1a ex ＋a e x. ∴⎝⎛⎭⎪⎫a －1a ⎝⎛⎭⎪⎫e x －1e x ＝0，此式对x ∈R 恒成立．∴a －1a ＝0.∴a ＝±1.又∵a >0，∴a ＝1.(2)证明：由(1)知f (x )＝e x ＋1e x ，设0<x 1<x 2，则f (x 1)－f (x 2)＝e x 1－e x 2＋1e x 1－1e x 2＝e x 1－e x 2＋e x 2－e x 1e x 1·e x 2＝(e x 1－e x 2)(e x 1＋x 2－1)e x 1＋x 2.∵0<x 1<x 2，∴e x 1<e x 2，e x 1＋x 2>1.∴f (x 1)<f (x 2)，∴f (x )在(0，＋∞)上是增函数．21．(本小题满分12分)某城市现有人口数为100万，如果年自然增长率为1.2%，试解答下面的问题．(1)写出该城市人口总数y (万人)与年份x (年)的函数关系式； (2)计算大约多少年以后，该城市人口将达到120万？(精确到1年)(lg 1.012≈0.0052，lg 1.2≈0.0792)解 (1)x 年后该城市人口总数y ＝100(1＋1.2%)x .(2)设x 年以后该城市人口将达到120万，即100(1＋1.2%)x ＝120，化简得1.012x ＝1.2.x ＝log 1.0121.2＝lg 1.2lg 1.012≈0.07920.0052≈16.所以大约16年以后，该城市人口将达到120万．22．(本小题满分12分)已知函数f (x )＝lg (a x －k ·b x )(k >0，a >1>b >0)的定义域为(0，＋∞)，是否存在这样的a 、b ，使得f (x )恰在(1，＋∞)上取正值，且f (3)＝lg 4？若存在，求出a 、b 的值；若不存在，请说明理由．解 由条件入手，其定义域为(0，＋∞)，∴a x－k ·b x>0的定义域即为(0，＋∞)，∴⎝ ⎛⎭⎪⎫a b x>k ，∵a ＞1＞b ＞0，∴ab ＞1，∴k ＝1，得f (x )＝lg (a x －b x )．假设存在满足条件的a 、b ，则f (3)＝lg (a 3－b 3)＝lg 4，∴a 3－b 3＝4 ①.∵a >1>b >0，∴u 1＝a x 为增函数，u 2＝b x 为减函数，∴g (x )＝a x －b x 为增函数．由f (x )恰在(1，＋∞)上取正值，可得f (1)＝lg (a －b )＝0，∴a －b ＝1 ②.由①②两式可得a 与b 的值，再由a >1>b >0，可得a ＝1＋52，b ＝－1＋52.。

必修1 综合检测(二)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，满分150分，考试时间120分钟．第Ⅰ卷 (选择题，共60分)一、选择题(本大题共12小题，每小题5分，共60分) 1．函数f(x)＝11－x ＋11＋x 的定义域是( )A ．(－∞，－1)B ．(1，＋∞)C ．(－1,1)∪(1，＋∞)D ．(－∞，＋∞)答案 C解析 由⎩⎪⎨⎪⎧1－x ≠01＋x>0得x>－1且x ≠1，故选C .2．下列各组函数中，表示同一函数的是( ) A ．y ＝1，y ＝x 0 B ．y ＝lg x 2，y ＝2lg x C ．y ＝|x|，y ＝(x)2D ．y ＝x ，y ＝3x 3答案 D解析 对于A ，当x ＝0时后者无意义；对于B 和C ，当x<0时前者有意义而后者无意义；D 显然正确．3．[2016·北大附中月考]已知集合A ＝{y|y ＝ln (x 2＋1)，x ∈R }，则∁R A ＝( )A ．∅B ．(－∞，0]C ．(－∞，0)D ．[0，＋∞)答案 C解析 ∵A ＝{y |y ＝ln (x 2＋1)，x ∈R }且x 2＋1≥1 ∴A ＝{y |y ≥0}， ∴∁R A ＝{y |y <0}，故选C.4．[2016·洛阳高一期中]设a ＝log 123，b ＝⎝ ⎛⎭⎪⎫130.2，c ＝⎝ ⎛⎭⎪⎫13－1，则( ) A ．a ＜b ＜cB ．c ＜b ＜aC ．c ＜a ＜bD ．b ＜a ＜c答案 A解析 因为log 12 3＜log 121＝0,0＜⎝ ⎛⎭⎪⎫130.2＜⎝ ⎛⎭⎪⎫130＝1，⎝ ⎛⎭⎪⎫13－1＝3＞1，所以正确的答案为A.5．已知函数f (x )是偶函数，且在区间[0,1]上是减函数，则f (－0.5)、f (－1)、f (0)的大小关系是( )A ．f (－0.5)<f (0)<f (－1)B ．f (－1)<f (－0.5)<f (0)C ．f (0)<f (－0.5)<f (－1)D ．f (－1)<f (0)<f (－0.5) 答案 B解析 因为函数f (x )是偶函数，所以f (－0.5)＝f (0.5)，f (－1)＝f (1)．又因为f (x )在区间[0,1]上是减函数，所以f (－1)<f (－0.5)<f (0)．6．[2016·福建宁德市联考]已知f (x )＝⎩⎪⎨⎪⎧x ＋(3a －4)，x <1a x ，x ≥1是R 上的增函数，则实数a 的取值范围是( )A.⎣⎢⎡⎭⎪⎫32，＋∞ B.⎝ ⎛⎦⎥⎤1，32 C ．(0,1) D ．(1，＋∞)答案 B解析 ∵f (x )是R 上的增函数，∴⎩⎪⎨⎪⎧a >1，1＋3a －4≤a ，解得：1<a ≤32，∴选B.7．[2016·河南商水一中]已知函数f (x )＝|lg x |－⎝ ⎛⎭⎪⎫12x有两个零点x 1，x 2，则有( )A ．x 1x 2<0B ．x 1x 2＝1C ．x 1x 2>1D ．0<x 1x 2<1答案 D解析 根据分析，不妨设0<x 1<1，x 2>1，根据函数零点的概念则有|lg x 1|－⎝ ⎛⎭⎪⎫12x 1＝0，|lg x 2|－⎝ ⎛⎭⎪⎫12x 2＝0，即－lg x 1＝⎝ ⎛⎭⎪⎫12 x 1，lg x 2＝⎝ ⎛⎭⎪⎫12 x2，后面的方程减去前面的方程得lg (x 1x 2)＝⎝ ⎛⎭⎪⎫12 x 2－⎝ ⎛⎭⎪⎫12 x1，由于x 2>x 1，根据指数函数的性质，⎝ ⎛⎭⎪⎫12 x 2－⎝ ⎛⎭⎪⎫12x1<0，所以lg (x 1x 2)<0，即0<x 1x 2<1.正确选项D.8．已知函数f (x )＝a x 在(0,2)内的值域是(a 2,1)，则函数y ＝f (x )的图象是( )答案 A解析 由f (x )＝a x 在(0,2)内的值域是(a 2,1)可知函数必为减函数，而且是指数函数，因此显然只有A 符合．9．设x >y >1,0<a <1，则下列关系正确的是( ) A ．x －a >y －a B ．ax <ay C ．a x <a y D ．log a x >log a y答案 C解析 对于A ，由0<a <1，可知－1<－a <0，因此函数y ＝x －a 为减函数，所以由x >y >1应得到x －a <y －a ，A 不正确；对于B ，由x >y >1,0<a <1，显然应得ax >ay ，B 不正确；对于C 、D ，由于0<a <1，所以函数y ＝a x 以及y ＝log a x 均为减函数，所以由x >y >1可得a x <a y 及log a x <log a y ，所以C 正确，D 不正确．所以选C.10．函数y ＝x 2与函数y ＝|lg x |的图象的交点个数为( ) A ．0 B ．1 C ．2D ．3答案 B解析 在同一平面直角坐标系中分别作出y ＝x 2和y ＝|lg x |的图象，如图，可得交点个数为1.11．当0<x ≤12时，4x <log a x ，则a 的取值范围是( )A.⎝⎛⎭⎪⎫0，22B.⎝ ⎛⎭⎪⎫22，1 C ．(1，2) D ．(2，2)答案 B 解析解法一：令f (x )＝4x ，g (x )＝log a x ，当x ＝12时，f ⎝ ⎛⎭⎪⎫12＝2.(如图)而g ⎝ ⎛⎭⎪⎫12＝log a 12＝2，∴a ＝22.又∵g (x )＝log a x ，x 0∈(0,1)，a 1，a 2∈(0,1)且a 1<a 2时，log a 2x 0>log a 1x 0，∴要使当0<x ≤12时，4x<log a x 成立，需22<a <1.故选B.解法二：∵0<x ≤12，∴1<4x ≤2，∴log a x >4x >1，∴0<a <1，排除答案C ，D ； 取a ＝12，x ＝12，则有412 ＝2，log 1212＝1，显然4x <log a x 不成立，排除答案A ；故选B.12．[2015·米易中学月考]函数y ＝ax 2＋bx 与y ＝log |b a|x (ab ≠0，|a |≠|b |)在同一直角坐标系中的图象可能是( )答案 D解析 若⎪⎪⎪⎪⎪⎪b a ＞1，y ＝log |b a |x 单调递增，A 、B 符合，此时⎪⎪⎪⎪⎪⎪b 2a ＞12，则由函数y ＝ax 2＋bx 的图象，A 、B 不符；若⎪⎪⎪⎪⎪⎪b a ＜1，y ＝log |b a | x 单调递减，C 、D 符合，此时⎪⎪⎪⎪⎪⎪b 2a ＜12，则由函数y ＝ax 2＋bx 的图象，C 不符，故选D.第Ⅱ卷 (非选择题，共90分)二、填空题(本大题共4小题，每小题5分，共20分)13．若函数f (x )＝(a 2－a －1)log (a ＋2)x 为对数函数，则f (64)＝________.答案 3解析由对数函数的定义可知需要满足⎩⎪⎨⎪⎧a 2－a －1＝1a ＋2>0a ＋2≠1，解得a＝2，所以f (x )＝log 4x ，f (64)＝3.14．[2016·辽宁名校期末]已知集合P ＝⎩⎨⎧⎭⎬⎫x ⎪⎪⎪13≤x ≤3，函数y ＝log 2(ax 2＋2x －2)的定义域为Q ，若P ∩Q ≠∅，则实数a 的取值范围是________．答案 ⎝ ⎛⎭⎪⎫－12，＋∞解析 若P ∩Q ≠∅，则在区间⎣⎢⎡⎦⎥⎤13，3上至少存在一个x 使ax 2＋2x －2>0成立，a >2⎝ ⎛⎭⎪⎫1x 2－1x ＝2⎣⎢⎡⎝ ⎛⎭⎪⎫1x －122⎦⎥⎤－14∈⎣⎢⎡⎦⎥⎤－12，12，所以a >－12.15．若定义在区间(1,2)内的函数f (x )＝log 3a (x －1)满足f (x )>0，则a 的取值范围是________．答案 0<a <13解析 当x ∈(1,2)时，x －1∈(0,1)，而此时必有 0<3a <1，因此0<a <13.16．对于函数f (x )＝x －2－ln x ，我们知道f (3)＝1－ln 3<0，f (4)＝2－ln 4>0，用二分法求函数f (x )在区间(3,4)内的零点的近似值，我们先求出函数值f (3.5)，若已知ln 3.5＝1.25，则接下来我们要求的函数值是______．答案 f (3.25)解析 由ln 3.5＝1.25且f (3.5)＝3.5－2－ln 3.5≈0.25>0，以及f (3)<0可知下一步应代入的x 值为3.5和3的平均数，即接下来我们需求的函数值为f (3.25)．三、解答题(本大题共6小题，满分70分)17．[2015·米易中学高一月考](本小题满分10分)函数f (x )＝4－x ＋lg (3x －9)的定义域为A ，集合B ＝{x |x －a ＜0，a ∈R }．(1)求集合A ；(2)若A ∩B ≠∅，求a 的取值范围．解 (1)要使函数f (x )有意义，只需满足⎩⎪⎨⎪⎧ 4－x ≥03x －9＞0，解得⎩⎪⎨⎪⎧x ≤4x ＞2，即2＜x ≤4，从而求出集合A ＝{x |2＜x ≤4}．(2)由(1)可得集合A ＝{x |2＜x ≤4}，而集合B ＝{x |x ＜a }，若a ≤2，则A ∩B ＝∅，所以a ＞2，即a 的取值范围是(2，＋∞)．18．[2016·梅县东山中学期中](本小题满分12分)已知函数f (x )＝1－23x ＋1. (1)求函数f (x )的定义域，判断并证明f (x )的奇偶性； (2)用单调性的定义证明函数f (x )在其定义域上是增函数； (3)解不等式f (3m ＋1)＋f (2m －3)<0.解 (1)∵3x >0，∴3x ＋1≠0，函数f (x )的定义域为R ，即(－∞，＋∞)．f (x )是奇函数．证明如下：∵f (x )的定义域为R ，又f (x )＝1－23＋1＝3x ＋1－23＋1＝3x －13x ＋1， ∴f (－x )＝3－x －13－x ＋1＝1－3x 3x 1＋3x 3x ＝1－3x1＋3x＝－f (x )，∴f (x )是定义在R 上的奇函数．(2)任取x 1，x 2∈R ，且x 1<x 2.则f (x 1)－f (x 2)＝1－23 x 1＋1－⎝ ⎛⎭⎪⎫1－23 x 2＋1＝23 x 2＋1－23 x 1＋1＝2(3 x 1＋1)－2(3x 2＋1)(3 x 1＋1)(3x 2＋1)＝2(3 x 1－3 x 2)(3 x 1＋1)(3 x 2＋1)，∵x 1<x 2，∴3 x 1<3 x 2，∴3 x 1－3 x 2<0， 又3 x 1＋1>0,3 x 2＋1>0， ∴f (x 1)－f (x 2)<0，即f (x 1)<f (x 2)， ∴函数f (x )在其定义域上是增函数．(3)由f (3m ＋1)＋f (2m －3)<0得f (3m ＋1)<－f (2m －3)， ∵函数f (x )为奇函数，∴－f (2m －3)＝f (3－2m )， ∴f (3m ＋1)<f (3－2m )．由(2)已证得函数f (x )在R 上是增函数， ∴f (3m ＋1)<f (3－2m )⇔3m ＋1<3－2m ，∴m <25.则不等式f (3m ＋1)＋f (2m －3)<0的解集为⎩⎨⎧⎭⎬⎫m ⎪⎪⎪m <25.19．[2015·成都高一质检](本小题满分12分)某工厂在政府的帮扶下，准备转型生产一种特殊机器，生产需要投入固定成本500万元，生产与销售均以百台计数，且每生产100台，还需增加可变成本1000万元．若市场对该产品的年需求量为500台，每生产m 百台的实际销售收入近似满足函数R (m )＝5000 m －500 m 2(0≤m ≤5，m ∈N )．(1)试写出第一年的销售利润y (万元)关于年产量x (单位：百台，x ≤5，x ∈N *)的函数关系式；(说明：销售利润＝实际销售收入－成本)(2)因技术等原因，第一年的年生产量不能超过300台，若第一年人员的年支出费用u (x )(万元)与年产量x (百台)的关系满足u (x )＝500x ＋500(x ≤3，x ∈N *)，问年产量x 为多少百台时，工厂所得纯利润最大？解 (1)由题意，y ＝5000x －500x 2－500－1000x ， 即y ＝－500x 2＋4000x －500(x ≤5，x ∈N *)． (2)记工厂所得纯利润为h (x )，则h (x )＝－500x 2＋4000x －500－u (x )＝－500x 2＋3500x －1000＝－500(x 2－7x )－1000＝－500⎝ ⎛⎭⎪⎫x －722＋5125(x ≤3，x ∈N *)． ∴当x ＝3(百台)时，h (x )max ＝5000.故当年生产量为300台时，厂家的纯利润最大，最大值为5000万元．20．[2015·杭州七校高一联考](本小题满分12分)已知函数f (x )＝a －2x4x ＋1(a ∈R )． (1)判断函数f (x )的奇偶性；(2)判断并证明函数f (x )在(0，＋∞)上的单调性． 解 (1)∵函数f (x )的定义域为R ，关于原点对称，∴f (－x )＝a －2－x 4－x ＋1＝a －4x 2x (1＋4x )＝a －2x4x ＋1＝f (x )，所以f (x )是偶函数．(2)判断：f (x )在(0，＋∞)上是单调递增函数； 证明：任取x 1，x 2∈(0，＋∞)且x 1<x 2， 则f (x 1)－f (x 2)＝(2 x 1－2 x 2)(2 x 1＋x 2－1)(4 x 1＋1)(4 x 2＋1).由0<x 1<x 2⇒2 x 1<2 x 2⇒2 x 1－2 x 2<0， 由0<x 1<x 2⇒2 x 1＋x 2>1， 2 x 1＋x 2>1⇒2 x 1＋x 2－1>0. 而4 x 1＋1>0,4 x 2＋1>0， 则f (x 1)－f (x 2)<0⇒f (x 1)<f (x 2)．所以f (x )在(0，＋∞)上是单调递增函数．21．(本小题满分12分)已知函数f (x )＝2a ·4x －2x －1. (1)当a ＝1时，求函数f (x )的零点； (2)若f (x )有零点，求a 的取值范围． 解 (1)当a ＝1时，f (x )＝2·4x －2x －1.令f (x )＝0，即2·(2x )2－2x－1＝0，解得2x＝1或2x＝－12(舍去)．∴x ＝0，∴函数f (x )的零点为x ＝0.(2)解法一：若f (x )有零点，则方程2a ·4x －2x －1＝0有解． 于是2a ＝2x ＋14x ＝⎝ ⎛⎭⎪⎫12x ＋⎝ ⎛⎭⎪⎫14x ＝⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫12x ＋122－14.∵⎝ ⎛⎭⎪⎫12x >0，∴2a >14－14＝0，即a >0.解法二：令t ＝2x ，∵x ∈R ，∴t >0， 则方程2at 2－t －1＝0在(0，＋∞)上有解．①当a ＝0时，方程为t ＋1＝0，即t ＝－1<0，此时方程在(0，＋∞)无解．②当a ≠0时，令g (t )＝2at 2－t －1，若方程g (t )＝0在(0，＋∞)上有一解，则ag (0)<0，即－a <0，解得a >0.若方程g (t )＝0在(0，＋∞)上有两解，则⎩⎨⎧ag (0)>0，Δ＝1＋8a ≥0，14a >0，解得a ∈∅.综上所述，所求实数a 的范围是(0，＋∞)．22．[2015·衡水高一调研](本小题满分12分)已知定义域为R 的函数f (x )满足f (f (x )－x 2＋x )＝f (x )－x 2＋x .(1)若f (2)＝3，求f (1)；又若f (0)＝a ，求f (a )；(2)设有且仅有一个实数x 0，使得f (x 0)＝x 0，求函数f (x )的解析表达式．解 (1)因为对任意x ∈R ，有f (f (x )－x 2＋x )＝f (x )－x 2＋x ， 所以f (f (2)－22＋2)＝f (2)－22＋2.又由f (2)＝3，得f (3－22＋2)＝3－22＋2， 即f (1)＝1.若f (0)＝a ，则f (a －02＋0)＝a －02＋0，即f (a )＝a .数学学习总结资料(2)因为对任意x∈R，有f(f(x)－x2＋x)＝f(x)－x2＋x.又因为有且只有一个实数x0，使得f(x0)＝x0，所以对任意x∈R，有f(x)－x2＋x＝x0.在上式中令x＝x0，有f(x0)－x20＋x0＝x0.又因为f(x0)＝x0，所以x0－x20＝0，故x0＝0或x0＝1.若x0＝0，则f(x)－x2＋x＝0，即f(x)＝x2－x.但方程x2－x＝x有两个不相同实根，与题设条件矛盾．故x0≠0.若x0＝1，则有f(x)－x2＋x＝1，即f(x)＝x2－x＋1.易验证该函数满足题设条件．综上，所求函数为f(x)＝x2－x＋1(x∈R)．数学学习。

加油！有志者事竟成答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。

２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，有什么题型，哪些容易，哪些难，做到心里有底；３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应该多读几遍，比如从小到大，从左到右这样的题；４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏的小题；５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读题，结合平时课堂上所学的知识，解答难题；一定要镇定，不能因此慌了手脚，影响下面的答题；６、卷面要清洁，字迹要清工整，非常重要；７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。

亲爱的朋友，你们好!经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。

相信你是最棒的！第三章综合测试一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）1.已知2()1f x x =+，则[(1)]f f -的值等于（ ） A .2B .3C .4D .5 2.已知函数()1f x x =+，其定义域为{1,0,1,2}-，则函数的值域为（ ） A .[0,3]B .{0,3}C .{0,1,2,3}D .{|0}y y3.函数0y =）A .{|01}x xB .{| 1 1}x x x --＜或＞C .{|01}x x x ≠-＜且D .{}|1 0x x x ≠-≠且4.已知二次函数()y f x =满足(2)(2)f x f x +=-，且函数图像截x 轴所得的线段长为8，则函数()y f x =的零点为（ ） A .2，6B .2，6-C .2-，6D .2-，6-5.若函数()y f x =的定义域是{|01}x x ≤≤，则函数()()(2)(01)F x f x a f x a a =+++＜＜的定义域是（ ）A .1|22a a x x -⎧⎫-⎨⎬⎩⎭≤B .|12a x x a ⎧⎫--⎨⎬⎩⎭≤C .{|1}x a x a --≤≤D .1|2a x a x -⎧⎫-⎨⎬⎩⎭≤≤6.如图所示，可表示函数()y f x =的图像的只可能是（ ）ABCD7.已知函数2()1f x ax bx =++为定义在[2,1]a a -上的偶函数，则a b +的值是（ ） A .1B .1-C .1或1-D .0或18.若()f x 满足()()f x f x -=-，且在(,0)-∞上是增函数，(2)0f -=，则()0xf x ＜的解集是（ ）A .(2,0)(0,2)-B .(,2)(0,2)-∞-C .(,2)(2,)-∞-+∞D .(2,0)(2,)-+∞9.设函数()f x 与()g x 的定义域是{|1}x x ∈≠±R ，函数()f x 是一个偶函数，()g x 是一个奇函数，且1()()1f xg x x -=-，则()f x 等于（ ） A .2221x x -B .211x -C .221x - D .221xx - 10.已知2()21(0)f x ax ax a =++＞，若()0f m ＜，则(2)f m +与1的大小关系式为（ ） A .(2)1f m +＜B .(2)1f m +=C .(2)1f m +＞D .(2)1f m +11.函数()f x =（ ） A .是奇函数但不是偶函数 B .是偶函数但不是奇函数 C .既是奇函数又是偶函数D .既不是奇函数又不是偶函数12.已知2()2f x x x =+，若存在实数t ，使()3f x t x + 对[1,]x m ∈恒成立，则实数m 的最大值是（ ） A .6B .7C .8D .9二、填空题（本大题共4小题，每小题5分，共20分.请把正确答案填在题中的横线上）13.已知1,[0,1],()2,[0,1],x f x x x ∈⎧=⎨-∉⎩，当[()]1f f x =时，x ∈__________.14.关于x 的方程240x x a --=有四个不相等的实数根，则实数a 的取值范围为__________.15.已知函数719()1x f x x +=+，则()f x 的图像的对称中心是__________，集合{}*|()x f x ∈=N __________. 16.已知函数()f x 是定义在实数集R 上的不恒为零的偶函数，且对任意实数x 都有(1)(1)()xf x x f x +=+，则52f f ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭的值是__________. 三、解答题（本大题共6小题，共70分，解答时写出必要的文字说明、证明过程或演算步骤） 17.（本小题满分10分）已知函数2()2||1f x x x =--.（1）利用绝对值及分段函数知识，将函数()f x 的解析式写成分段函数； （2）在坐标系中画出()f x 的图像，并根据图像写出函数()f x 的单调区间和值域.18.（本小题满分12分）已知函数()f x 对任意实数x 均有()2(1)f x f x =-+，且()f x 在区间[0]1，上有解析式2()f x x =.（1）求(1)f -和(1.5)f 的值；（2）写出()f x 在区间[2,2]-上的解析式.19.（本小题满分12分）函数2()1ax bf x x +=+是定义在(,)-∞+∞上的奇函数，且1225f ⎛⎫= ⎪⎝⎭. （1）求实数a ，b 的值.（2）用定义证明()f x 在(1,1)-上是增函数；（3）写出()f x 的单调减区间，并判断()f x 有无最大值或最小值.如有，写出最大值或最小值（无需说明理由）.20.（本小题满分12分）已知定义域为R 的单调函数()f x ，且(1)f x -的图像关于点(1,0)对称，当0x ＞时，1()3x f x x=-. （1）求()f x 的解析式； （2）若对任意的t ∈R ，不等式()()22220f t t f t k -+-＜恒成立，求实数k 的取值范围.21.（本小题满分12分）对于定义域为D 的函数()y f x =，若同时满足下列条件：①()f x 在D 内单调递增或单调递减；②存在区间[,]a b D ⊆，使()f x 在[,]a b 上的值域为[,]a b ，那么称()()x D y f x =∈为闭函数. （1）求闭函数3y x =-符合条件②的区间[,]a b . （2）判断函数31()(0)4f x x x x=+＞是否为闭函数？并说明理由；（3）判断函数y k =+是否为闭函数？若是闭函数，求实数k 的取值范围.22.（本小题满分12分）设函数()f x 的定义域为R ，当0x ＞时，()1f x ＞，对任意,x y ∈R ，都有()()()f x y f x f y += ，且(2)4f =.（1）求(0)f ，(1)f 的值.（2）证明：()f x 在R 上为单调递增函数.（3）若有不等式1()2f x f x x ⎛⎫+ ⎪⎝⎭ ＜成立，求x 的取值范围.第三章测试 答案解析一、 1.【答案】D【解析】由条件知(-1)2f =，(2)5f =，故选D . 2.【答案】C【解析】将x 的值依次代入函数表达式可得0，1，2，3，所以函数的值域为{0,1,2,3}，故选C . 3.【答案】C【解析】由条件知10x +≠且0x x -＞，解得0x ＜且1x ≠-.故选C 4.【答案】C【解析】由于函数()y f x =满足(2)(2)f x f x +=-，所以直线2x =为二次函数()y f x =图像的对称轴，根据二次函数图像的性质，图像与x 轴的交点必关于直线2x =对称.又两交点间的距高为8，则必有两交点的横坐标分别为1246x =+=，2242x =-=-.故函数的零点为2-，6.故选C . 5.【答案】A【解析】由条件知01,021,x a x a +⎧⎨+⎩，又01a ＜＜则122a ax --≤，故选A .6.【答案】D【解析】由函数定义可得，任意一个x 有唯一的y 与之对应，故选D . 7.【答案】B【解析】因为函数2()1f x ax bx =++为定义在[2,1]a a -上的偶函数，所以21a a =-，1a =-，0b =，因此1a b +=-，故选B.8.【答案】A【解析】根据题意可知函数是奇函数，且在(,0)-∞，(0,)+∞上是增函数，对()0xf x ＜，分0x ＞，0x ＜进行讨论，可知解集为(2,0)(0,2)- ，故选A. 9.【答案】B【解析】1()()1f x g x x -=-∵，1()()1f x g x x ---=--∴，1()()1f xg x x +=--∴， 21122()111f x x x x =-=-+-∴，21()1f x x =-，故选B . 10.【答案】C【解析】因为2()21(0)f x ax ax a =++＞，所以其图像的对称轴为直线1x =-，所以()(2)0f m f m =--＜，又(0)1f =，所以(2)1f m +＞，故选C .11.【答案】A【解析】由定义城可知x()f x =，那么根据函数的奇偶性的定义，可知该函数是奇函数不是偶函数，故选A . 12.【答案】C【解析】由题意知，对任意[1,]x m ∈，2()2()3x t x t x +++ 恒成立，这个不等式可以理解为()f x t +的图像在直线3y x =的图像的下面时x 的取值范围.要使m 最大，需使两图像交点的横坐标分别为1和m .当1x =时，3y =，代入可求得4t =-（0t =舍去）.进而求得另一个交点为(8,24)，故8m =.故选C. 二、13.【答案】[0,1][2,3]{5}【解析】因为1,[0,1],()2,[0,1],x f x x x ∈⎧=⎨-∉⎩所以要满足元[()]1f f x =，需()[0,1]f x ∈，[0,1]x ∈或2[0,1]x -∈或5x =，这样解得x 的取值范围是[0,1][2,3]{5} .14.【答案】(0,4)【解析】原方程等价于24x x a -=，在同一坐标系内作出函数24y x x =-与函数y a =的图像，如图所示：平移直线y a =，可得当04a ＜＜时，两图像有4个不同的公共点，相应地方程240x x a --=有4个不相等的实数根，综上所述，可得实数a 的范围为04a ＜＜. 15.(1,7)- {13,7,5,4,3,0,1,2,3,5,11}----- 【解析】因为函数71912()711x f x x x +==+++，则()f x 的图像的对称中心为(1,7)-， 集合{|()}{13,7,5,4,3,0,1,2,3,5,11}x f x *∈=-----N 16.【答案】0【解析】因为()f x 是定义在R 上的偶函数，因此令12x =-，可知11112222f f ⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭，所以102f ⎛⎫= ⎪⎝⎭，分别令32x =-，52x =-，可得302f ⎛⎫= ⎪⎝⎭，502f ⎛⎫= ⎪⎝⎭，令1x =-.得(0)0f =，因此可知502f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭. 三、17.【答案】（1）22321,0()2||121,0x x x f x x x x x x ⎧--=--=⎨+-⎩＜ .（2）图像如图所示.单调增区间为(1,0)-，(1,)+∞， 单调减区间为(,1)-∞-，(0,1). 值域为[2,)-+∞.18.【答案】（1）由题意知(1)2(11)2(0)0f f f -=--+=-=，1111(1,5)(10.5)(0.5)2248f f f =+=-=-⨯=-. （2）当[0,1]x ∈时，2()f x x =； 当(1,2]x ∈时，1(0,1]x -∈，211()(1)(1)22f x f x x =--=--； 当[1,0)x ∈-时，1[0,1)x +∈， 2()2(1)2(1)f x f x x =-+=-+；当[2,1)x ∈--时，1[1,0)x +∈-，22()2(1)22(11)4(2)f x f x x x ⎡⎤=-+=-⨯-++=+⎣⎦. 所以22224(2),[2,1),2(1),[1,0),(),[0,1],1(1),(1,2].2x x x x f x x x x x ⎧+∈--⎪-+∈-⎪⎪=⎨∈⎪⎪--∈⎪⎩19.【答案】（1）2()1ax bf x x +=+∵是奇函数()()f x f x -=-∴， 2211ax b ax bx x -++=-++∴，0b =∴.故2()1ax f x x =+，又1225f ⎛⎫= ⎪⎝⎭∵，1a =∴ （2）证明：由（1）知2()1xf x x =+，任取1211x x -＜＜＜，()()()()()()1212121222121211111x x x x x x f x f x x x x x ---=-=++++1211x x -∵＜＜＜，1211x x -∴＜＜，120x x -＜，1210x x -＞，2110x +＞，2210x +＞，()()120f x f x -∴＜，即()()12f x f x ＜，()f x ∴在(1,1)-上是增函数.（3）单调减区间为(,1),(1,)-∞-+∞.当1x =-时，min 1()2f x =-；当1x =时，max 1()2f x =.20.【答案】（1）由题意知()f x 的图像关于点(0,0)对称，是奇函数，∴(0)0f = 当0x ＜时，0x -＞，1()3x f x x--=--∴， 又∵函数()f x 是奇函数.∴()()f x f x -=-，1()3x f x x=-∴. 综上所述，1(0),()30(0).x x f x x x ⎧-≠⎪=⎨⎪=⎩（2）2(1)(0)03f f =-=∵，且()f x 在R 上单调.∴()f x 在R 上单调递减.由()()22220f t t f t k -+-＜，得()()2222f t t f t k ---＜.∵()f x 是奇函数，∴()()2222f t t f k t --＜，又∵()f x 是减函数， ∴2222t t k t --＞即2320t t k --＞对任意t ∈R 恒成立，∴4120k ∆=+＜，得13k -＜.21.【答案】（1）由题意，3y x =-，在[,]a b 上单调递减，则33,,,b a a b b a ⎧=-⎪=-⎨⎪>⎩解得1,1,a b =-⎧⎨=⎩所以，所求区间为[1,1]-.（2）取11x =，210x =，则()()1273845f x f x ==＜，即()f x 不是(0,)+∞上的减函数.取，1110x -=，21100x =，()()12331010040400f x f x =++=＜，即()f x 不是(0,)+∞上的增函数.所以，函数在定义域内不单调递增或单调递减，从而该函数不是闭函数.（3）若y k =是闭函数，则存在区间[,]a b ，在区间[,]a b 上，函数()f x 的值域为[,]a b，即a kb k ⎧=⎪⎨=⎪⎩∴a ，b为方程x k =+的两个实根， 即方程22(21)20(2,)x k x k x x k -++-=- 有两个不等的实根，故两根均大于等于2-，且对称轴在直线2x =-的右边.当2k - 时，有220,(2)2(21)20,212,2k k k ⎧⎪∆⎪-+++-⎨⎪+⎪-⎩＞ 解得924k -- .当2k -＞时，有220,(21)20,21,2k k k k k k ⎧⎪∆⎪-++-⎨⎪+⎪⎩＞ 无解.综上所述，9,24k ⎛⎤∈-- ⎥⎝⎦.22.【答案】（1）因为(20)(2)(0)f f f += ，所以44(0)f =⋅，所以(0)1f =， 又因为24(2)(11)(1)f f f ==+=，且当0x ＞时，()1f x ＞，所以(1)2f =.（2）证明：当0x ＜时，0x -＞，所以()1f x -＞，而(0)[()]()()f f x x f x f x =+-=- ， 所以1()()f x f x =-，所以0()1f x ＜＜，对任意的12,x x ∈R ， 当12x x ＜时，有()()()]()()()1212222121f x f x f x x x f x f x f x x -=⎡-+-=--⎣， 因为120x x ＜＜，所以120x x -＜，所以()1201f x x -＜＜，即()1210f x x --＜， 所以()()120f x f x -＜，即()()12f x f x ＜，所以()f x 在R 上是单调递增函数.（3）因为1()12f x f x ⎛⎫+ ⎪⎝⎭ ＜，所以11(1)f x f x ⎛⎫++ ⎪⎝⎭＜，而()f x 在R 上是单调递增函数，所以111x x ++＜，即10x x+＜，所以210x x +，所以0x ＜，所以x 的取值范围是(,0)-∞.。

第三章单元测试题（金属及其化合物）可能用到的相对原子质量：H— 1 O —16 S —32 Cu —64 Fe —56Na-23 Al —27第I卷选择题（共48分）一、选择题（本题包括8小题，每小题3分，共24分。

每小题只有一个选项符合题意。

）1. 实验室中，通常将金属钠保存在（）2下列物质中，不属于合金的是（）3. 下列物质中既能跟稀H2SO反应,又能跟氢氧化钠溶液反应的是（）①NaHCO ②AbQ ③AI（OH）3 ④AlA. ③④B.②③④C.①③④D.全部4. 镁、铝、铜三种金属粉末混合物，加入过量盐酸充分反应，过滤后向滤液中加入过量烧碱溶液，再过滤，滤液中存在的离子有（）A . AIS- B. CiT C . Al3+ D . Mg+5. 下列离子方程式书写正确的是（）A. 铝粉投入到NaOH溶液中：2AI+2OH—— 2AIO2_+H4B. AICI 3溶液中加入足量的氨水：Al3++ 3OH —— AI（OH） 3 J3 + 2 +C. 三氯化铁溶液中加入铁粉：Fe F^2FeD. FeCb溶液跟CI2反应：2Fe2++Cl2=2FeT+2C「6. 下列离子在溶液中能大量共存的是（）A Fe3+、NH * SCN - CI 一B Na 弋H 弋NO 厂SO：一C Fe2、Fe3、Na、NO TD Fe2、NH 4、CI - OH -7. 常温下，将等物质的量的Fe粉和Cu粉加入过量的浓HNO中，充分反应后, 溶液中存在的金属阳离子是（）A.只有Fe3+ B .只有Fe2+ C.只有Ci J+ D.有Ci J+和Fe3+8. 将适量铁粉放入FeCI a溶液中，完全反应后，溶液中的Fe2+和Fe3+溶度相等,则已反应的Fe3+和未反应的Fe3+的物质的量之比是（）A. 2 : 3 B . 3 : 2 C . 1 : 2 D二、选择题（本题包括4小题，每小题6分，共24分。

每小题只有一个或两个选项符合题意。

【金版学案】2016-2017学年高中数学 第三章 函数的应用单元评估验收 新人教版必修1(时间：120分钟 满分：150分)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项符合题目要求)1．二次函数f (x )＝2x 2＋bx －3(b ∈R)的零点个数是( ) A ．0 B ．1 C ．2 D ．4解析：因为Δ＝b 2＋4×2×3＝b 2＋24>0，所以函数图象与x 轴有两个不同的交点，故函数有2个零点．答案：C2．函数y ＝1＋1x的零点是( )A ．(－1，0)B ．－1C ．1D ．0解析：令1＋1x＝0，得x ＝－1，即为函数的零点．答案：B3．已知幂函数y ＝f (x )的图象经过点⎝ ⎛⎭⎪⎫－2，－18，则满足f (x )＝27的x 的值为( ) A ．3 B.127 C ．27 D.13解析：因为幂函数y ＝x a 的图象经过点⎝ ⎛⎭⎪⎫－2，－18，所以(－2)a＝－18，所以a ＝－3.又因为f (x )＝27，所以x －3＝27，所以x ＝13.答案：D4．若函数f (x )＝2mx ＋4在区间[－2，1]上存在x 0使得f (x 0)＝0，则实数m 的取值范围是( )A.⎣⎢⎡⎦⎥⎤－52，4 B ．[－2，1]C ．[－1，2]D ．(－∞，－2]∪[1，＋∞)解析：因为函数f (x )＝2mx ＋4在区间[－2，1]上存在x 0使得f (x 0)＝0，所以f (－2)·f (1)≤0，解得m ≤－2或m ≥1. 答案：D5．函数f (x )＝ln x －2x的零点所在的大致区间( )A ．(1，2)B ．(2，3)C ．(3，4)与(1，e)D ．(e ，＋∞)解析：易知函数f (x )在(2，3)上是连续的，且f (2)＝ln 2－1＝ln 2－ln e ＝ln 2e<0，f (3)＝ln 3－23>0，所以函数f (x )的零点所在的大致区间是(2，3)．答案：B6．函数f (x )＝2x－1的零点是( ) A ．0 B ．－1 C ．1 D ．2解析：由2x－1＝0，得x ＝0，故函数的零点为0. 答案：A7．已知x 0是函数f (x )＝2x －1x －1的一个零点．若x 1∈(1，x 0)，x 2∈(x 0，＋∞)，则( ) A ．f (x 1)<0，f (x 2)>0 B ．f (x 1)<0，f (x 2)<0 C ．f (x 1)>0，f (x 2)<0D ．f (x 1)>0，f (x 2)>0解析：易知f (x )在区间(1，＋∞)上为增函数，且f (x 0)＝0，x 1∈(1，x 0)，x 2∈(x 0，＋∞)，所以f (x 1)<0，f (x 2)>0.答案：A8．甲用1 000元人民币购买了一手股票，随即他将这手股票卖给乙，获利10%，而后乙又将这手股票卖给甲，但乙损失了10%，最后甲又按乙卖给甲的价格的九成将这手股票卖给了乙．在上述股票交易中( )A ．甲刚好盈亏平衡B ．甲盈利9元C ．甲盈利1元D ．甲亏本1.1元解析：甲两次付出为1 000元和1 000×1110×910元，两次收入为1 000×1110元和1 000×1110×910×910元， 而1 000×1110＋1 000×1110×910×910－1 000－1 000×1110×910＝1，故甲盈利1元．答案：C9．方程log 12x ＝2x －1的实根个数是( ) A ．0 B ．1 C ．2 D ．无穷多个x与y＝2x－1的图象(图略)可知，两曲线仅有一个交点，故实根个解析：画出y＝log12数为1.答案：B10．某城市为保护环境、维护水资源，鼓励职工节约用水，作出了如下规定：每月用水不超过8吨，按每吨2元收取水费，每月用水超过8吨，超过部分加倍收费．若某职工某月缴水费20元，则该职工这个月实际用水( )A．10吨 B．13吨 C．11吨 D．9吨解析：设该职工该月实际用水为x吨，易知x>8，则水费y＝16＋2×2(x－8)＝4x－16＝20，所以x＝9.答案：D11．设甲、乙两地的距离为a km(a>0)，小王骑自行车匀速从甲地到乙地用了20 min，在乙地休息10 min后，又匀速从乙地返回甲地用了30 min.则小王从出发到返回原地所经过的路程y和其所用的时间x的函数图象为( )解析：由题意知，中间休息时，时间与路程之间的函数为常函数，其余时间段随时间的增加，路程也增加．观察图象知D选项正确．答案：D12．函数y＝f(x)是定义在R上的连续不断的一条曲线，满足f(a)·f(b)<0，f(b)·f(c)<0，其中a<b<c，则y＝f(x)在(a，c)上零点个数为( )A．2 B．至少2个C．奇数D．偶数解析：因为函数y＝f(x)是定义在R上的连续不断的一条曲线，由f(a)·f(b)<0，知y ＝f(x)在(a，b)上至少有1个零点，由f(b)·f(c)<0知y＝f(x)在(b，c)上至少有1个零点，所以y＝f(x)在(a，c)上至少有2个零点．答案：B二、填空题(本大题共4小题，每小题5分，共20分．把答案填在题中横线上) 13．若f (x )是定义域为R 的奇函数，且在区间(0，＋∞)上有一个零点，则f (x )的零点个数为________．解析：由题意知f (0)＝0，f (x )在区间(0，＋∞)上有一个零点，在区间(－∞，0)上也必有一个零点，所以f (x )在定义域R 上有三个零点．答案：314．已知函数f (x )＝x 2＋ax －1的一个零点大于1，另一个零点小于1，则实数a 的取值范围是 ___________．解析：根据该二次函数的图象可以，实数a 的取值满足f (1)<0，即12＋a －1<0，得a <0. 答案：(－∞，0)15．一种产品的产量原来为a ，在今后m 年内，计划使产量每年比上一年增加p %，则产量y 随年数x 变化的函数解析式为______________；定义域为________________．解析：该函数是指数函数，解析式为y ＝a (1＋p %)x，定义域为{x |0≤x ≤m ，x ∈N}． 答案：a (1＋p %)x{x |0≤x ≤m ，x ∈N}16．给出封闭函数的定义：若对于定义域D 内的任意一个自变量x 0，都有函数值f (x 0)∈D ，则称函数f (x )在D 上封闭．若定义域D ＝(0，1)，则下列函数：①f 1(x )＝3x －1；②f 2(x )＝1－x ；③f 3(x )＝x 12.其中在D 上封闭的是________(填函数的序号)．解析：因为f 1(13)＝0∉(0，1)，所以f 1(x )在D 上不封闭．因为f 2(x )＝1－x 在(0，1)上是减函数，所以0＝f 2(1)<f 2(x )<f 2(0)＝1，所以f 2(x )在D 上封闭．因为f 3(x )＝x 12在区间(0，1)上是增函数，所以0＝f 3(0)<f 3(x )<f 3(1)＝1，所以f 3(x )在D 上封闭．答案：②③三、解答题(本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤) 17．(本小题满分10分)某市出租车的计价标准是4 km 以内10元(含4 km)，超过4 km 且不超过18 km 的部分1.2元/千米，超出18 km 的部分1.8元/千米．(1)不计等待时间的费用，建立车费与行车里程的函数关系式； (2)如果某人乘车行驶了20 km ，那么他要付多少车费？ 解：(1)设行车里程为x km ，车费为y 元．由题意得， y ＝⎩⎪⎨⎪⎧10，0<x ≤4，10＋1.2（x －4），4<x ≤18，10＋1.2×14＋1.8（x －18），x >18，即y ＝⎩⎪⎨⎪⎧10，0<x ≤4，1.2x ＋5.2，4<x ≤18，1.8x －5.6，x >18.(2)将x ＝20代入函数解析式，得y ＝1.8×20－5.6＝30.4(元)． 故乘车20 km ，要付车费30.4元．18．(本小题满分12分)已知函数f (x )＝x 2＋(m －2)x ＋5－m 有两个零点，且都大于2，求实数m 的取值范围．解：函数f (x )＝x 2＋(m －2)x ＋5－m 有两个大于2的零点，即方程x 2＋(m －2)x ＋5－m ＝0有两个不相等的实数解，且都大于2.结合图象可知⎩⎪⎨⎪⎧（m －2）2－4（5－m ）>0，2－m2>2，4＋2（m －2）＋5－m >0，解得－5<m <－4.故实数m 的取值范围是(－5，－4)．19．(本小题满分12分)已知矩形ABCD ，|AB |＝4，|AD |＝1，点O 为线段AB 的中点．动点P 沿矩形ABCD 的边从B 逆时针运动到A .当点P 运动过的路程为x 时，记点P 的运动轨迹O 与线段OP 、OB 围成的图形面积为f (x )．(1)求f (x )表达式； (2)若f (x )＝2，求x 的值．解：(1)当x ∈[0，1]时，f (x )＝12·OB ·x ＝x ；当x ∈(1，5]时，f (x )＝（2＋x －1）·12＝12(x ＋1)；当x ∈(5，6]时，f (x )＝4×1－12×2·(6－x )＝x －2.所以f (x )＝⎩⎪⎨⎪⎧x ， 0≤x ≤1，12（x ＋1），1<x ≤5，x －2， 5<x ≤6.(2)若f (x )＝2，显然1<x ≤5， 所以f (x )＝12(x ＋1)＝2，解得x ＝3.20．(本小题满分12分)某同学在用120分钟做150分的数学试卷(分为卷Ⅰ和卷Ⅱ两部分)时，卷Ⅰ和卷Ⅱ所得分数分别为P (单位：分)和Q (单位：分)，在每部分做了20分钟的条件下发现它们与投入时间m (单位：分钟)的关系有经验公式，P ＝15m ＋36，Q ＝65＋23m .(1)试建立数学总成绩y (单位：分)与对卷Ⅱ投入时间x (单位：分钟)的函数关系式，并指明函数定义域；(2)如何计划使用时间，才能使得所得分数最高．解：(1)设对卷Ⅱ用x 分钟，则对卷Ⅰ用(120－x )分钟，所以y ＝P ＋Q ＝65＋23x ＋15(120－x )＋36＝－15x ＋23x ＋125，其定义域为[20，100]． (2)令t ＝x ∈[25，10]， 则函数为关于t 的二次函数：y ＝－15t 2＋23t ＋125＝－15(t －53)2＋140.所以当t ＝53，即x ＝75时，y max ＝140.即当卷Ⅰ用45分钟，卷Ⅱ用75分钟时，所得分数最高．21．(本小题满分12分)已知关于x 的二次函数f (x )＝x 2＋(2t －1)x ＋1－2t . (1)求证：对于任意t ∈R，方程f (x )＝1必有实数根；(2)若12<t <34，求证：方程f (x )＝0在区间(－1，0)和⎝ ⎛⎭⎪⎫0，12内各有一个实数根． 证明：(1)由f (x )＝1得x 2＋(2t －1)x ＋1－2t ＝1， 即x 2＋(2t －1)x －2t ＝0.因为Δ＝(2t －1)2＋8t ＝4t 2＋4t ＋1＝(2t ＋1)2≥0， 所以对于任意t ∈R，方程f (x )＝1必有实数根． (2)当12<t <34时，f (－1)＝3－4t ＝4⎝ ⎛⎭⎪⎫34－t >0， f (0)＝1－2t ＝2⎝ ⎛⎭⎪⎫12－t <0，f ⎝ ⎛⎭⎪⎫12＝14＋12(2t －1)＋1－2t ＝34－t >0，故方程f (x )＝0在区间(－1，0)和⎝ ⎛⎭⎪⎫0，12内各有一个实数根． 22．(本小题满分12分)某企业从2010年开始生产一种出口产品，根据需求预测：前8年在正常情况下，该产品产量将平衡增长．已知2010年为第一年，前4年年产量f (x )(万件)如下表所示：(1)画出2010～(2)建立一个能基本反映(误差小于0.1)这一时期该企业年产量发展变化的函数模型，并求出该函数模型；(3)2016年(即x ＝7)因受到国外对我国该产品反倾销的影响，年产量应减少30%，试根据所建立的函数模型，确定2016年的年产量应约为多少？解：(1)散点图如图所示．(2)设f (x )＝ax ＋b .由已知得⎩⎪⎨⎪⎧a ＋b ＝4，3a ＋b ＝7，解得a ＝32，b ＝52，所以f (x )＝32x ＋52.检验：f (2)＝5.5，|5.58－5.5|＝0.08<0.1；f (4)＝8.5，|8.44－8.5|＝0.06<0.1.故函数模型f (x )＝32x ＋52能基本反映该企业年产量发展变化．(3)由题意知，f (7)＝32×7＋52＝13.故2016年的年产量应约为13×70%＝9.1(万件)．。

最新人教版数学精品教学资料第三章单元质量评估时限：120分钟 满分：150分一、选择题(每小题5分，共60分)1．若函数y ＝f (x )在区间[a ，b ]上的图象为连续不断的一条曲线，则下列说法正确的是( )A ．若f (a )f (b )>0，则不存在实数c ∈(a ，b )使得f (c )＝0B ．若f (a )f (b )<0，则只存在一个实数c ∈(a ，b )，使得f (c )＝0C ．若f (a )f (b )>0，则有可能存在实数c ∈(a ，b )使得f (c )＝0D ．若f (a )f (b )<0，则有可能不存在实数c ∈(a ，b )使得f (c )＝0 2．函数y ＝f (x )在区间(－2,2)上的图象是连续的，且方程f (x )＝0在(－2,2)上仅有一个实根0，则f (－1)·f (1)的值( )A ．大于0B ．小于0C ．等于0D ．无法确定3．若函数f (x )在[a ，b ]上的图象为连续不断的一条曲线，且同时满足f (a )f (b )<0，f (a )·f (a ＋b 2)>0，则( )A ．f (x )在[a ，a ＋b2]上有零点 B ．f (x )在[a ＋b2，b ]上有零点 C ．f (x )在[a ，a ＋b2]上无零点 D ．f (x )在[a ＋b2，b ]上无零点4．函数f (x )＝1－x ln x 的零点所在的区间是( ) A ．(0，12) B ．(12，1) C ．(1,2)D ．(2,3)5．设f (x )＝3x ＋3x －8，若用二分法求方程3x ＋3x －8＝0在区间(1,2)内的近似解的过程中得f (1)<0，f (1.5)>0，f (1.25)<0，则方程的根所在的区间为( )A ．(1,1.25)B ．(1.25,1.5)C ．(1.5,2)D ．不能确定6．若函数f (x )＝x 2＋3x ＋2，且f (a )>f (b )>0，则函数f (x )的区间(a ，b )内( )A ．一定无零点B ．一定有零点C ．可能有两个零点D ．至多有一个零点7．如图所示，液体从一圆锥形漏斗漏入一圆柱形桶中，开始时，漏斗中盛满液体，经过3分钟漏完．已知圆柱中液面上升的速度是一个常量，H 是圆锥形漏斗中液面下落的高度，则H 与下落时间t (分钟)的函数关系表示的图象可能是( )8．某辆汽车每次加油都把油箱加满，下表记录了该车相邻两次加油时的情况在这段时间内，该车每100千米平均耗油量为( ) A ．6升 B ．8升 C ．10升D ．12升9．某市生产总值连续两年持续增加．第一年的增长率为p ，第二年的增长率为q ，则该市这两年生产总值的年平均增长率为( )A.p ＋q 2B.(p ＋1)(q ＋1)－12C.pqD.(p ＋1)(q ＋1)－110．设a 是函数f (x )＝2x －log 12x 的零点，若x 0>a ，则( ) A ．f (x 0)＝0 B ．f (x 0)>0C ．f (x 0)<0D ．f (x 0)的符号不确定11．已知f (x )是定义在R 上的奇函数，当x ≥0时，f (x )＝x 2－3x .则函数g (x )＝f (x )－x ＋3的零点的集合为( )A ．{1,3}B ．{－3，－1,1,3}C ．{2，－7，1,3}D ．{－2－7，1,3}12．已知函数f (x )＝⎩⎪⎨⎪⎧2－|x |，x ≤2，(x －2)2，x >2，函数g (x )＝b －f (2－x )，其中b ∈R .若函数y ＝f (x )－g (x )恰有4个零点，则b 的取值范围是( )A ．(74，＋∞) B ．(－∞，74) C ．(0，74)D ．(74，2) 答案1．C 当零点在区间(a ，b )内时，f (a )f (b )>0也可能成立，因此A 不正确，C 正确；若y ＝f (x )满足零点存在性定理的两个条件，则在该区间内必存在零点，但个数不能确定，故B ，D 都不正确．2．D 由题意，知f (x )在(－1,1)上有零点0，该零点可能是变号零点，也可能是不变号零点，∴f (－1)·f (1)的符号不确定，如f (x )＝x 2，f (x )＝x .3．B 由f (a )f (b )<0，f (a )f (a ＋b 2)>0可知f (a ＋b2)f (b )<0，根据零点存在性定理可知f (x )在[a ＋b2，b ]上有零点． 4．C 由于f (1)＝1－ln1＝1>0，f (2)＝1－2ln2＝lne －ln4<0，由零点存在性定理可知所求区间为(1,2)．5．B ∵f (1)<0，f (1.5)>0，f (1.25)<0，∴f (1.5)·f (1.25)<0，因此方程的根所在的区间为(1.25,1.5)．6．C 根据二次函数的图象可知选项C 正确．7．B 由于所给的圆锥形漏斗上口大于下口，当时间取12t 时，漏斗中液面下落的高度不会达到漏斗高度的12，对比四个选项的图象可知选B.8．B 因为第一次(即5月1日)把油加满，而第二次把油加满加了48升，即汽车行驶35 600－35 000＝600千米耗油48升，所以每100千米的耗油量为8升，选B.9．D 设年平均增长率为x ，原生产总值为a ，则(1＋p )(1＋q )a ＝a (1＋x )2，解得x ＝(1＋p )(1＋q )－1，故选D.10．B 如图所示，画出函数y ＝2x 与y ＝log 12x 的图象，可知当x 0>a 时，2x0>log 12x 0，故f (x 0)>0.11．D 当x ≥0时，函数g (x )的零点即方程f (x )＝x －3的根，由x 2－3x ＝x －3，解得x ＝1或3.当x <0时，由f (x )是奇函数得－f (x )＝f (－x )＝x 2－3(－x )，即f (x )＝－x 2－3x .由f (x )＝x －3得x ＝－2－7(正根舍去)．故选D.12．D 函数y ＝f (x )－g (x )恰有4个零点，即方程f (x )－g (x )＝0，即b ＝f (x )＋f (2－x )有4个不同的实数根，即直线y ＝b 与函数y ＝f (x )＋f (2－x )的图象有4个不同的交点．又y ＝f (x )＋f (2－x )＝⎩⎪⎨⎪⎧x 2＋x ＋2，x <0，2，0≤x ≤2，x 2－5x ＋8，x >2，作出该函数的图象如图所示，由图可得，当74<b <2时，直线y ＝b 与函数y ＝f (x )＋f (2－x )的图象有4个不同的交点，故函数y ＝f (x )－g (x )恰有4个零点时，b 的取值范围是(74，2)．———————————————————————————— 二、填空题(每小题5分，共20分)13．已知定义在R 上的函数f (x )的图象是连续不断的，且有如下部分对应值表：14．用二分法求函数f (x )的一个零点，其参考数据如下：为________．15．某食品的保鲜时间y (单位：小时)与储藏温度x (单位：℃)满足函数关系y ＝e kx ＋b (e ＝2.718…为自然对数的底数，k ，b 为常数)．若该食品在0℃的保鲜时间是192小时，在22℃的保鲜时间是48小时，则该食品在33℃的保鲜时间是________小时．16．设函数f (x )＝⎩⎪⎨⎪⎧2x －a ，x <1，4(x －a )(x －2a )，x ≥1.若f (x )恰有2个零点，则实数a 的取值范围是________．三、解答题(写出必要的计算步骤、解答过程，只写最后结果的不得分，共70分)17．(10分)(1)判断函数f (x )＝x 3－x －1在区间[－1，2]上是否存在零点；(2)求函数y ＝x ＋2x －3的零点．18．(12分)若函数f (x )为定义在R 上的奇函数，且当x >0时，f (x )＝ln x ＋2x －6，试判断函数f (x )的零点个数．答案13.3解析：由已知数据可知f (2)f (3)<0，f (3)f (4)<0，f (4)f (5)<0，所以函数在区间(2,3)，(3,4)，(4,5)内各至少有1个零点，则函数至少有3个零点．14．1.562 5(答案不唯一)解析：由参考数据知，f (1.562 5)≈0.003>0，f (1.556 25)≈－0.029<0，即f (1.556 25)·f (1.562 5)<0，又1.562 5－1.556 25＝0.006 25<0.01，∴f (x )的一个零点的近似值可取为1.562 5.15．24解析：由题意得⎩⎪⎨⎪⎧e b＝192，e 22k ＋b ＝48，即⎩⎨⎧e b＝192，e 11k ＝12，所以该食品在33℃的保鲜时间是y ＝e33k ＋b＝(e 11k )3·e b＝(12)3×192＝24(小时)．16．[12，1)∪[2，＋∞)解析：当a ≥1时，要使f (x )恰有2个零点，需满足21－a ≤0，即a ≥2，所以a ≥2；当a <1时，要使f (x )恰有2个零点，需满足⎩⎪⎨⎪⎧a <1≤2a ，21－a >0，解得12≤a <1.综上，实数a 的取值范围为[12，1)∪[2，＋∞)．17．解：(1)∵f (－1)＝－1<0，f (2)＝5>0，f (－1)f (2)<0.∴f (x )在[－1,2]上存在零点．(2)x ＋2x －3＝x 2－3x ＋2x ＝(x －1)(x －2)x ，解方程x ＋2x －3＝0，即(x －1)(x －2)x＝0，可得x ＝1或x ＝2.∴函数y ＝x ＋2x －3的零点为1,2. 18．解：方法一：当x <0时，－x >0，f (－x )＝ln(－x )－2x －6，又f (x )为奇函数，所以f (x )＝－f (－x )＝－ln(－x )＋2x ＋6.故函数f (x )的解析式为f (x )＝⎩⎪⎨⎪⎧ln x ＋2x －6，x >00，x ＝0－ln (－x )＋2x ＋6，x <0令f (x )＝0易得函数f (x )有3个零点．方法二：当x >0时，在同一坐标系中作出函数y ＝ln x 和y ＝6－2x 的图象如图所示，易知两函数图象只有1个交点，即当x >0时，函数f (x )有1个零点．由f (x )为定义在R 上的奇函数，可知f (0)＝0，且图象关于原点对称，则当x <0时，函数f (x )有1个零点．综上可知，f (x )在R 上有3个零点．———————————————————————————— 19．(12分)已知二次函数f (x )＝x 2＋bx ＋c ，且方程f (x )＋4＝0有唯一解x ＝1.(1)求函数f (x )的解析式；(2)若函数f (x )在区间[a ，a ＋4]上存在零点，求实数a 的取值范围．(12分)某医药研究所开发的一种新药，如果成年人按规定的剂量服用，据监测：服药后每毫升血液中的含药量y(mg)与时间t(h)之间近似满足如图所示的曲线．(1)写出服药后y与t之间的函数关系式y＝f(t)；(2)据进一步测定：每毫升血液中含药量不少于0.25 mg时，对治疗疾病有效，求服药一次治疗疾病有效的时间．答案19.解：(1)方程f (x )＋4＝0有唯一解x ＝1，即一元二次方程x 2＋bx ＋c ＋4＝0有唯一解x ＝1，则⎩⎪⎨⎪⎧ b 2－4(c ＋4)＝0，b ＋c ＋5＝0，⇒⎩⎪⎨⎪⎧b ＝－2，c ＝－3， 所以f (x )＝x 2－2x －3.(2)结合(1)易知函数f (x )的零点为－1,3.当－1∈[a ，a ＋4]时，－5≤a ≤－1；当3∈[a ，a ＋4]时，－1≤a ≤3.故实数a 的取值范围为[－5,3]．20．解：(1)当0≤t <1时 ，y ＝4t ；当t ≥1时，y ＝⎝ ⎛⎭⎪⎫12t －a 此时M (1,4)在曲线上， 故4＝⎝ ⎛⎭⎪⎫121－a ，解得a ＝3，即y ＝⎝ ⎛⎭⎪⎫12t －3. 故y ＝f (t )＝⎩⎨⎧4t ，0≤t <1，⎝ ⎛⎭⎪⎫12t －3，t ≥1. (1)因为f (t )≥0.25，则⎩⎨⎧ 4t ≥0.25，⎝ ⎛⎭⎪⎫12t －3≥0.25. 解得⎩⎨⎧ t ≥116，t ≤5，所以116≤t ≤5，因此服药一次治疗疾病有效的时间为5－116＝41516(h)．————————————————————————————21．(12分)设f(x)为定义在R上的偶函数，当x≥0时，f(x)＝－(x －2)2＋2.(1)求函数f(x)在R上的解析式；(2)在直角坐标系中画出函数f(x)的图象；(3)若方程f(x)－k＝0有四个解，求实数k的取值范围．22.(12分)人们对声音有不同的感觉，这与它的强度I(单位：W/m2)有关系．但在实际测量时，常用声音的强度水平L1(单位：dB)表示，它满足公式：L1＝10×lg II0(L1≥0，其中I0＝1×10－12W/m2，这是人们平均能听到的最小强度，是听觉的开端)．根据以上材料，回答下列问题：(1)树叶沙沙声的强度是1×10－12W/m2，耳语声的强度是1×10－10W/m2，恬静的无线电广播声的强度是1×10－8W/m2，试分别求出它们的强度水平；(2)某一新建的安静小区规定：小区内公共场所的声音的强度水平必须保持在50 dB以下，试求声音的强度I的范围是多少？答案21.解：(1)由于f (x )为定义在R 上的偶函数，则f (－x )＝f (x )， 若x <0，则－x >0，f (x )＝f (－x )＝－(－x －2)2＋2＝－(x ＋2)2＋2，则f (x )＝⎩⎪⎨⎪⎧－(x －2)2＋2，x ≥0，－(x ＋2)2＋2，x <0. (2)图象如图所示：(3)由于方程f (x )－k ＝0的解就是函数y ＝f (x )的图象与直线y ＝k 的交点的横坐标，观察函数y ＝f (x )的图象可知，当－2<k <2时，函数y ＝f (x )的图象与直线y ＝k 有四个交点，即方程f (x )－k ＝0有四个解．22．解：(1)由题意可知，树叶沙沙声的强度是I 1＝1×10－12W/m 2，则I 1I 0＝1，所以LI 1＝10×lg1＝0，即树叶沙沙声的强度水平为0 dB. 耳语声的强度是I 2＝1×10－10W/m 2，则I 2I 0＝102，所以LI 2＝10×lg102＝20，即耳语声的强度水平为20 dB.恬静的无线电广播声的强度是I 3＝1×10－8 W/m 2，则I 3I 0＝104，所以LI 3＝10×lg104＝40，即恬静的无线电广播声的强度水平为40 dB.(2)由题意知，0≤L1<50，即0≤10×lg II0<50，所以1≤II0<105，即10－12≤I<10－7.所以小区内公共场所的声音的强度I的范围为大于或等于10－12W/m2，同时应小于10－7W/m2.。

第三章 单元质量测评(一)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，满分150分，考试时间120分钟．第Ⅰ卷 (选择题，共60分)一、选择题(本大题共12小题，每小题5分，共60分) 1．下列函数中没有零点的是( ) A ．f (x )＝log 2x －7 B ．f (x )＝x －1 C ．f (x )＝1x D ．f (x )＝x 2＋x答案 C解析 由于函数f (x )＝1x 中，对任意自变量x 的值，均有1x ≠0，故该函数不存在零点．2．若函数f (x )＝ax 2＋x ＋1有零点，则a 的取值范围是( ) A.⎝⎛⎦⎥⎤－∞，14B.⎣⎢⎡⎭⎪⎫14，＋∞ C.⎝ ⎛⎭⎪⎫－∞，14 D ．{0}答案 A解析 由题意得ax 2＋x ＋1＝0有解，当a ＝0时， x ＝－1；当a ≠0时，Δ＝1－4a ≥0，解得a ≤14，综上a ≤14.3．[2016·山东枣庄八中月考]方程ln x ＋x －4＝0的实根所在的区间为( )A ．(1,2)B ．(2,3)C ．(3,4)D ．(4,5)答案 B解析 设函数f (x )＝ln x ＋x －4(x >0)，故f (x )是(0，＋∞)上的单调递增函数．因为f (2)·f (3)＝(ln 2－2)(ln 3－1)<0，故函数f (x )在区间(2,3)上有零点，即方程ln x ＋x －4＝0在区间(2,3)上有实根，故选B.4．[2015·米易中学高一月考]函数f (x )＝x ＋lg x －3的零点所在区间为( )A ．(3，＋∞)B ．(2,3)C ．(1,2)D ．(0,1)答案 B解析 因为函数f (x )在(0，＋∞)上单调递增，且f (2)＝2＋lg 2－3＝lg 2－1＜0，而f (3)＝3＋lg 3－3＝lg 3＞0，所以在区间(2,3)上必存在函数的零点．5．[2016·北大附中月考]某车间分批生产某种产品，每批的生产准备费用为800元．若每批生产x 件，则平均仓储时间为x8天，且每件产品每天的仓储费用为1元．则平均每件产品的生产准备费用与仓储费用之和S (元)关于x (件)的函数是( )A ．S ＝800＋x8 B ．S ＝800x ＋x8 C ．S ＝800x ＋x8 D ．S ＝800x ＋x 答案 C解析 由题意知每件产品的生产准备费用是800x 元，仓储费用是x8×1元，所以每件产品的生产准备费用与仓储费用之和S ＝800x ＋x 8，故选C.6．[2016·西城高一期末]函数f (x )＝1x －ln x 的零点个数为( ) A ．0 B ．1 C ．2 D ．3答案 B解析 如图，在同一坐标系中作出y ＝1x 与y ＝ln x 的图象： 可知f (x )＝1x －ln x 只有一个零点．7．如图所示，阴影部分的面积S 是h 的函数(0≤h ≤H )，则该函数的图象是()答案 C解析 当h ＝H2时，对应阴影部分的面积小于整个图形面积的一半，且随着h 的增大，S 随之减小，故排除A 、B 、D.8．[2016·广东深圳中学期中]某商场在国庆促销期间，规定商场内所有商品按标价的80%出售，同时，当顾客在该商场内消费满一定金额后，按如下方案可以再获得相应金额的奖券，购买标价为400元的商品，则消费金额为320元，获得的优惠额为400×0.2＋30＝110(元)．若顾客购买一件标价为1000元的商品，则获得的优惠额为()A．130元B．330元C．360元D．800元答案 B解析根据题意，消费金额为800元，所以优惠额为1000×0.2＋130＝330(元)，故选B.9．[2016·清华附中期末考试]已知函数y＝f(x)和y＝g(x)在[－2,2]上的图象如图所示，则下列结论正确的是()A．方程f(g(x))＝0有且仅有6个实根B．方程g(f(x))＝0有且仅有5个实根C．方程f(f(x))＝0有且仅有4个实根D．方程g(g(x))＝0有且仅有5个实根答案 A解析(1)满足f(x)＝0的x值在区间[－2,2]上有三个，把这三个值看作g(x)对应的y值，则当g(x)等于这三个值中的每个时，都有两个x值与之对应，故方程f(g(x))＝0有且仅有6个根；(2)满足g(x)＝0的x值在区间[－2,2]上有两个，一个在区间(－2，－1)上，一个在区间(0,1)上，把这两个值看作f(x)对应的y值，则当f(x)等于区间(－2，－1)上的值时，只有一个x值与之对应，当f(x)等于区间(0,1)上的值时，有三个x值与之对应，故方程g(f(x))＝0有且只有4个根；(3)满足f(x)＝0的x值在区间[－2,2]上有三个，把这三个值再看作f(x)对应的y值，当f(x)等于区间(－2，－1)上的值时，只有一个x值与之对应，当f(x)等于区间(1,2)上的值时，也只有一个x值与之对应，当f(x)等于区间(－1,1)上的值时，所对应的x值有三个，故方程f(f(x))＝0有且仅有5个根；(4)同样的方法可知方程g(g(x))＝0有且仅有4个根．故选A.10．利用计算器，列出自变量和函数值的对应值如下表：A．(0.6,1.0) B．(1.4,1.8)C．(1.8,2.2) D．(2.6,3.0)答案 C解析构造f(x)＝2x－x2，则f(1.8)＝0.242，f(2.2)＝－0.245，故在(1.8,2.2)内存在一点使f(x)＝2x－x2＝0，所以方程2x＝x2的一个根就位于区间(1.8,2.2)上．x的零点，若0<x1<x0，则f(x1) 11．已知x0是函数f(x)＝2x－log13的值满足()A．f(x1)>0B．f(x1)<0C．f(x1)＝0D．f(x1)>0与f(x1)<0均有可能答案 B解析由于f(x)在(0，＋∞)上是增函数，所以f(x1)<f(x0)＝0.12．用长度为24 m的材料围成一矩形场地，并且中间加两道隔墙，要使矩形的面积最大，则隔墙的长度为()A．3 m B．4 mC．5 m D．6 m答案 A解析 设隔墙的长为x m ，矩形面积为S ，则S ＝x ·24－4x2＝x (12－2x )＝－2x 2＋12x ＝－2(x －3)2＋18，所以当x ＝3时，S 有最大值为18.第Ⅱ卷 (非选择题，共90分)二、填空题(本大题共4小题，每小题5分，共20分) 13．已知函数f (x )＝x 2－1，则函数f (x －2)的零点是________． 答案 1或3解析 f (x －2)＝(x －2)2－1＝x 2－4x ＋3＝0，x ＝1或x ＝3. 14．若函数f (x )＝x 2＋mx ＋m ＋3的一个零点在原点，则另一个零点是________．答案 3解析 函数f (x )＝x 2＋mx ＋m ＋3的一个零点在原点，则f (0)＝0，∴m ＋3＝0，∴m ＝－3.则f (x )＝x 2－3x ，于是另一个零点是3.15．[2016·江苏天一中学期末]已知函数f (x )＝x 2＋x ＋a 在区间(0,1)上有零点，则实数a 的取值范围是________．答案 (－2,0)解析 函数f (x )＝x 2＋x ＋a 在(0,1)上单调递增．由已知得f (0)f (1)<0，则a (a ＋2)<0，即⎩⎨⎧ a >0a ＋2<0或⎩⎨⎧a <0a ＋2>0，解得－2<a <0.16．[2015·衡水中学高一月考]里氏震级是由两位来自美国加州理工学院的地震学家里克特(C.F.Richter)和古登保(B.Gutenberg)于1935年提出的一种震级标度．里氏震级M 的计算公式是M ＝lg A －lg A 0，其中A 是被测地震的最大振幅，A 0是“标准地震”的振幅.2011年3月11日，日本东北部海域发生里氏9.0级地震并引发海啸，造成重大人员伤亡和财产损失．一般里氏6级地震给人的震撼已十分强烈，按照里氏震级M 的计算公式，此次日本东北部大地震的最大振幅是里氏6级地震最大振幅的________倍．答案 1000解析 设里氏6级地震最大振幅为A 6，里氏9级地震最大振幅为A 9，所以⎩⎪⎨⎪⎧9＝lg A 9－lg A 06＝lg A 6－lg A 0，解得lg A 9－lg A 6＝3，即lg A 9A 6＝3，所以A 9A 6＝103＝1000.三、解答题(本大题共6小题，满分70分)17．(本小题满分10分)讨论函数y ＝(ax －1)(x －2)的零点． 解 当a ＝0时，函数为y ＝－x ＋2，故其零点为x ＝2； 当a ≠0时，零点为x 1＝1a ，x 2＝2.18．(本小题满分12分)在泰山早晨观日出气温较低，为方便游客，一家旅馆备有120件棉衣提供出租，每件日租金50元，每天都客满．五一假期即将来临，该旅馆准备提高租金．经调查，如果每件的日租金每增加5元，则每天出租会减少6件，不考虑其他因素，棉衣日租金提到多少元时，棉衣日租金的总收入最高？解 设每件棉衣日租金提高x 个5元，即提高5x 元，则每天棉衣减少出租6x 件，又设棉衣日租金的总收入为y 元．∴y ＝(50＋5x )×(120－6x )， ∴y ＝－30(x －5)2＋6750∴当x ＝5时，y max ＝6750，这时每件棉衣日租金为50＋5x ＝50＋5×5＝75(元)，∴棉衣日租金提到75元时，棉衣日租金的总收入最高，最高为6750元．19．[2016·湖北荆州中学期末](本小题满分12分)已知函数f (x )＝ax 3－2ax ＋3a －4在区间(－1,1)上有一个零点．(1)求实数a 的取值范围；(2)若a ＝3217，用二分法求方程f (x )＝0在区间(－1,1)上的根． 解 (1)若a ＝0，则f (x )＝－4，与题意不符，∴a ≠0. 由题意得f (－1)·f (1)＝8(a －1)(a －2)<0，即⎩⎪⎨⎪⎧ a －1<0a －2>0或⎩⎪⎨⎪⎧a －1>0a －2<0， ∴1<a <2，∴实数a 的取值范围为(1,2)． (2)若a ＝3217，则f (x )＝3217x 3－6417x ＋2817， ∴f (－1)＝6017>0，f (0)＝2817>0，f (1)＝－417<0，∴函数零点在(0,1)上，又f ⎝ ⎛⎭⎪⎫12＝0，∴方程f (x )＝0在区间(－1,1)上的根为12.20．[2016·成都七中高一月考](本小题满分12分)成都市出租车的现行计价标准是：路程在2 km 以内(含2 km)按起步价8元收取，超过2 km 后的路程按1.9元/km 收取，但超过10 km 后的路程需加收50%的返空费(即单价为1.9×(1＋50%)＝2.85元/km)．(1)将某乘客搭乘一次出租车的费用f (x )(单位：元)表示为行程x (0<x ≤60，单位：km)的分段函数；(2)某乘客的行程为16 km ，他准备先乘一辆出租车行驶8 km 后，再换乘另一辆出租车完成余下行程，请问：他这样做是否比只乘一辆出租车完成全部行程更省钱？(现实中要计等待时间且最终付费取整数，本题在计算时都不予考虑)解 (1)由题意得，车费f (x )关于路程x 的函数为： f (x )＝⎩⎪⎨⎪⎧8，(0<x ≤2)8＋1.9(x －2)，(2<x ≤10)8＋1.9×8＋2.85(x －10)，(10<x ≤60)＝⎩⎪⎨⎪⎧8，(0<x ≤2)4.2＋1.9x ，(2<x ≤10)2.85x －5.3，(10<x ≤60).(2)只乘一辆车的车费为：f (16)＝2.85×16－5.3＝40.3(元)；换乘2辆车的车费为：2f(8)＝2×(4.2＋1.9×8)＝38.8(元)．∵40.3>38.8，∴该乘客换乘比只乘一辆车更省钱．21．[2016·石家庄市一中期中](本小题满分12分)一种放射性元素，最初的质量为500 g，按每年20%衰减．(1)求t(t＞0，t∈N*)年后，这种放射性元素的质量y与t的函数关系式；(2)求这种放射性元素的半衰期(质量变为原来的12时所经历的时间)．(lg 2≈0.3)解(1)最初的质量为500 g，经过1年，y＝500(1－20%)＝500×0.8，经过2年，y＝500(1－20%)2＝500×0.82，经过t年，y＝500(1－20%)t＝500×0.8t，∴y＝500×0.8t(t∈N*)．(2)解方程500×0.8t＝250，两边取常用对数t lg 0.8＝lg 0.5，t＝－lg 23lg 2－1＝－0.33×0.3－1＝3，即这种放射性元素的半衰期约为3年．22．(本小题满分12分)甲商店某种商品4月份(30天，4月1日为第一天)的销售价格P(元)与时间t(天)的函数关系如下图(1)所示，该商品日销售量Q(件)与时间t(天)的函数关系如下图(2)所示．(1)写出图(1)表示的销售价格与时间的函数关系式P＝f(t)，写出图(2)表示的日销售量与时间的函数关系式Q＝g(t)，及日销售金额M (元)与时间的函数关系式M ＝h (t )；(2)乙商店销售同一种商品，在4月份采用另一种销售策略，日销售金额N (元)与时间t (天)之间的函数关系式为N ＝－2t 2－10t ＋2750，比较4月份每天两商店销售金额的大小．解 (1)设销售价格函数是y ＝kt ＋b ，由图(1)知该函数图象过点(0,15)，(30,30)，所以⎩⎪⎨⎪⎧b ＝15，30k ＋b ＝30，解得⎩⎨⎧b ＝15，k ＝12.∴P ＝f (t )＝12t ＋15(0<t ≤30，t ∈N *)．日销售量函数是y ＝at ＋m ，由图(2)知该函数图象过点(0,160)，(30,40)，所以⎩⎪⎨⎪⎧ m ＝160，30a ＋m ＝40，解得⎩⎪⎨⎪⎧m ＝160，a ＝－4.∴Q ＝g (t )＝－4t ＋160(0<t ≤30，t ∈N *)．故M ＝h (t )＝⎝ ⎛⎭⎪⎫12t ＋15(－4t ＋160)＝－2t 2＋20t ＋2400(0<t ≤30，t ∈N *)． (2)由N ＝－2t 2－10t ＋2750(t ∈N *)， 可得M －N ＝30t －350(0<t ≤30，t ∈N *)． 由30t －350<0，知0<t <1123，t ∈N *.即前11天甲商店销售金额比乙商店少，以后甲均比乙多．。

第一章单元质量测评(二)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，满分150分，考试时间120分钟．第Ⅰ卷(选择题，共60分)一、选择题(本大题共12小题，每小题5分，共60分)1．已知M＝{x|x>2或x<0}，N＝{y|y＝x－1}，则N∩(∁R M)等于()A．(1,2) B．[0,2]C．∅D．[1,2]答案 B解析因为M＝{x|x>2或x<0}，所以∁R M＝[0,2]，又N＝{y|y＝x－1}＝[0，＋∞)，故N∩(∁R M)＝[0,2]．2．[2016·太原五中高一月考]下列四个命题中，设U为全集，则不正确的命题是()A．若A∩B＝∅，则(∁U A)∪(∁U B)＝UB．若A∪B＝∅，则A＝B＝∅C．若A∪B＝U，则(∁U A)∩(∁U B)＝∅D．若A∩B＝∅，则A＝B＝∅答案 D解析若A＝{2}，B＝{3}，则A∩B＝∅.∴D不正确，选D.3．已知集合A＝{y|y＝－x2－2x}，B＝{x|y＝x－a}，且A∪B＝R，则实数a的最大值是()A．1 B．－1C．0 D．2答案 A解析根据题意，得A＝(－∞，1]，B＝[a，＋∞)，因为A∪B＝R ，画出数轴可知a ≤1，即实数a 的最大值是1.4．[2016·广西桂林中学段考]已知函数f (x )＝12－x 的定义域为M ，g (x )＝x ＋2的定义域为N ，则M ∩N ＝( )A ．{x |x ≥－2}B ．{x |x <2}C ．{x |－2<x <2}D ．{x |－2≤x <2}答案 D解析 ∵M ＝{x |x <2}，N ＝{x |x ≥－2}，∴M ∩N ＝{x |－2≤x <2}，故选D.5．使根式x －1与x －2分别有意义的x 的允许值集合依次为M 、F ，则使根式x －1＋x －2有意义的x 的允许值集合可表示为( )A ．M ∪FB ．M ∩FC ．∁M FD ．∁F M 答案 B解析 根式x －1＋x －2有意义，必须x －1与x －2同时有意义才可．6．给出下列集合A 到集合B 的几种对应：其中，是从A到B的映射的是()A．(1)(2) B．(1)(2)(3)C．(1)(2)(4) D．(1)(2)(3)(4)答案 A解析根据映射的定义知，(3)中集合A中元素a对应集合B中两个元素x，y，则此对应不是映射；(4)集合A中b在集合B中没有对应元素，且集合A中c对应集合B中两个元素y，z，则此对应不是映射．仅有(1)(2)是映射．7．某厂日产手套总成本y(元)与手套日产量x(双)的关系为y＝5x ＋4000.而手套出厂价格为每双10元，则该厂为了不亏本，日产手套至少为()A．200双B．400双C．600双D．800双答案 D解析若不亏本，则10x≥5x＋4000，所以x≥800.8．已知函数f(x)＝x2－4x＋10，x∈[－1，m]，并且f(x)的最小值为f(m)，则实数m的取值范围是()A．(－1,2] B．(－1，＋∞)C ．[2，＋∞)D ．(－∞，－1)答案 A解析 f (x )＝x 2－4x ＋10＝(x －2)2＋6，x ∈[－1，m ]，对称轴x ＝2，且f (x )min ＝f (m )，∴－1<m ≤2，故选A.9．已知定义在R 上的偶函数f (x )，对任意x 1，x 2∈[0，＋∞)(x 1≠x 2)，有f (x 2)－f (x 1)x 2－x 1<0，则( )A ．f (3)<f (－2)<f (1)B ．f (1)<f (－2)<f (3)C ．f (－2)<f (1)<f (3)D ．f (3)<f (1)<f (－2) 答案 A解析 由题意知f (x )为偶函数，所以f (－2)＝f (2)，又x ∈[0，＋∞)时，f (x )为减函数，且3>2>1，∴f (3)<f (2)<f (1)， 即f (3)<f (－2)<f (1)，故选A.10．[2016·人大附中月考]已知函数f (x )为奇函数，在区间[3,6]上是增函数，且在此区间上的最大值为8，最小值为－1，则2f (－6)＋f (－3)＝( )A ．－15B ．－13C ．－5D ．5答案 A解析 因为函数在[3,6]上是增函数，所以f (6)＝8，f (3)＝－1，又函数f (x )为奇函数，所以2f (－6)＋f (－3)＝－2f (6)－f (3)＝－2×8＋1＝－15，故选A.11．[2016·石家庄高一检测]函数y ＝f (x )与y ＝g (x )的图象如图，则函数y ＝f (x )·g (x )的图象可能是( )答案 A解析 由图可知f (x )的图象关于y 轴对称，g (x )的图象关于原点对称，∴f (x )是偶函数，g (x )是奇函数，∴y ＝f (x )·g (x )是奇函数，排除B ，且y ＝f (x )·g (x )的定义域为(－∞，0)∪(0，＋∞)，故选A.12．[2016·太原五中高一月考]若f (x )＝|x ＋1|－|x －1|，则f (x )的值域为( )A ．RB ．[－2,2]C ．[－2，＋∞)D ．[2，＋∞)答案 B解析f (x )＝|x ＋1|－|x －1|＝⎩⎪⎨⎪⎧－2，x <－1，2x ，－1≤x ≤1，2，x >1.当－1≤x ≤1时，－2≤2x ≤2， ∴f (x )的值域为[－2,2]，选B.第Ⅱ卷 (非选择题，共90分)二、填空题(本大题共4小题，每小题5分，共20分)13．[2016·江苏扬州中学期中]集合A ＝{x |(a －1)x 2＋3x －2＝0}的子集有且仅有两个，则实数a ＝________.答案 1或－18解析 集合的子集有且仅有两个，则这个集合只有一个元素，因此本题中集合A 只有一个元素，说明方程(a －1)x 2＋3x －2＝0只有一个解(一次方程)或者有两个相等实根(二次方程)．当a ＝1时，方程3x －2＝0有一解x ＝23； 当a ≠1时，Δ＝32－4×(a －1)×(－2)＝0， 解得a ＝－18，故a ＝1或－18.14．函数f (x )＝3x ＋2在[－5，－4]上的值域是________．答案⎣⎢⎡⎦⎥⎤－32，－1 解析 ∵f (x )在[－5，－4]上单调递减， f (－5)＝3－5＋2＝－1，f (－4)＝3－4＋2＝－32.∴f (x )∈⎣⎢⎡⎦⎥⎤－32，－1. 15．f (x )，g (x )都是定义在R 上的奇函数，且F (x )＝3f (x )＋5g (x )＋2，若F (a )＝b ，则F (－a )＝________.答案 －b ＋4解析 ∵函数f (x )，g (x )均为奇函数， ∴f (a )＋f (－a )＝0，g (a )＋g (－a )＝0，∴F (a )＋F (－a )＝3f (a )＋5g (a )＋2＋3f (－a )＋5g (－a )＋2＝4，∴F (－a )＝4－F (a )＝4－b .16．[2015·江苏盐城中学月考]若函数f (x )＝kx 2＋(k －1)x ＋3是偶函数，则f (x )的递减区间是________．答案 (－∞，0]解析 ∵f (x )是偶函数，∴f (－x )＝f (x )，即k (－x )2＋(k －1)(－x )＋3＝kx 2＋(k －1)x ＋3，即kx 2－(k －1)x ＋3＝kx 2＋(k －1)x ＋3，∴－(k －1)＝k －1，∴k ＝1，即f (x )＝x 2＋3.此函数图象为开口向上且以y 轴为对称轴的抛物线，所以f (x )的递减区间是(－∞，0]．三、解答题(本大题共6小题，满分70分)17．[2015·哈尔滨三中检测](本小题满分10分)已知全集为实数集R ，集合A ＝{x |1≤x ≤7}，B ＝{x |－2m ＋1<x <m }．(1)若m ＝5，求A ∪B ，(∁R A )∩B ； (2)若A ∩B ＝A ，求m 的取值范围．解 (1)∵m ＝5，∴B ＝{x |－9<x <5}，又A ＝{x |1≤x ≤7}，∴A ∪B ＝{x |－9<x ≤7}．又∁R A ＝{x |x <1或x >7}， ∴(∁R A )∩B ＝{x |－9<x <1}． (2)∵A ∩B ＝A ，∴A ⊆B ，∴⎩⎨⎧－2m ＋1<1m >7，即⎩⎨⎧m >0m >7，解得m >7.∴m 的取值范围是{m |m >7}．18．[2015·江苏盐城中学期中](本小题满分12分)设函数f (x )＝x 2－4|x |－5.(1)画出y ＝f (x )的图象；(2)方程f (x )＝k ＋1有两解，求实数k 的取值范围．解 (1)f (x )＝x 2－4|x |－5＝⎩⎪⎨⎪⎧x 2－4x －5，x ≥0x 2＋4x －5，x ＜0图象如图①所示．(2)由图象②分析可知当方程f (x )＝k ＋1有两解时，k ＋1＝－9或k ＋1＞－5，∴k ＝－10或k ＞－6.19．(本小题满分12分)已知函数f (x )＝x 2＋ax (x ≠0，a ∈R )．(1)判断函数f (x )的奇偶性；(2)若f (x )在区间[2，＋∞)上为增函数，求实数a 的取值范围． 解 (1)当a ＝0时，f (x )＝x 2为偶函数； 当a ≠0时，f (x )既不是奇函数也不是偶函数． (2)设x 2>x 1≥2，f (x 1)－f (x 2)＝x 21＋a x 1－x 22－a x 2＝x 1－x 2x 1x 2[x 1x 2(x 1＋x 2)－a ]，由x 2>x 1≥2，得x 1x 2(x 1＋x 2)>16， x 1－x 2<0，x 1x 2>0.要使f (x )在区间[2，＋∞)上是增函数， 只需f (x 1)－f (x 2)<0，即x 1x 2(x 1＋x 2)－a >0恒成立，则a ≤16.20．[2016·湖南师大附中高一考试](本小题满分12分)经市场调查，某门市部的一种小商品在过去的20天内的日销售量(件)与价格(元)均为时间t (天)的函数，且日销售量近似满足函数g (t )＝80－2t (件)，而且销售价格近似满足于f (t )＝⎩⎪⎨⎪⎧15＋12t (0≤t ≤10)25－12t (10<t ≤20)(元)．(1)试写出该种商品的日销售额y 与时间t (0≤t ≤20)的函数表达式；(2)求该种商品的日销售额y 的最大值与最小值． 解 (1)由已知得：y ＝⎩⎪⎨⎪⎧⎝ ⎛⎭⎪⎫15＋12t (80－2t )(0≤t ≤10)⎝ ⎛⎭⎪⎫25－12t (80－2t )(10<t ≤20)＝⎩⎪⎨⎪⎧－t 2＋10t ＋1200(0≤t ≤10)t 2－90t ＋2000(10<t ≤20)(2)由(1)知①当0≤t ≤10时，y ＝－t 2＋10t ＋1200＝－(t －5)2＋1225.该函数在t ∈[0,5]递增，在t ∈(5,10]递减．∴y max ＝1225(当t ＝5时取得)，y min ＝1200(当t ＝0或10时取得)． ②当10<t ≤20时，y ＝t 2－90t ＋2000＝(t －45)2－25. 该函数在t ∈(10,20]递减，y min ＝600(当t ＝20时取得)．由①②知y max ＝1225(当t ＝5时取得)，y min ＝600(当t ＝20时取得)． 21．[2016·玉溪中学高一期中](本小题满分12分)已知奇函数f (x )＝⎩⎪⎨⎪⎧－x 2＋2x (x ＞0)0(x ＝0)x 2＋mx (x ＜0)(1)求实数m 的值，并画出y ＝f (x )的图象；(2)若函数f (x )在区间[－1，|a |－2]上单调递增，试确定实数a 的取值范围．解 (1)∵函数f (x )是奇函数，∴f (－1)＝－f (1)，即1－m ＝－1，∴m ＝2.因此，f (x )＝⎩⎪⎨⎪⎧－x 2＋2x (x ＞0)0(x ＝0)x 2＋2x (x ＜0)，所以函数f (x )图象为：(2)从函数f (x )图象可知f (x )的单调递增区间是[－1,1]，∴－1＜|a |－2≤1.因此实数a 的取值范围是{a |1＜a ≤3或－3≤a ＜－1}． 22．[2016·海南中学高一期中](本小题满分12分)已知函数f (x )＝mx 2＋23x ＋n是奇函数，且f (2)＝53. (1)求实数m 和n 的值；(2)判断f (x )在区间(0，＋∞)上的单调性，并加以证明． 解 (1)∵f (x )＝mx 2＋23x ＋n是奇函数，∴对任意x ∈R ，且x ≠－n3都有f (－x )＋f (x )＝0，即mx 2＋2－3x ＋n ＋mx 2＋23x ＋n ＝0，亦即2n (mx 2＋2)(－3x ＋n )(3x ＋n )＝0，于是n ＝0. 又f (2)＝53，即4m ＋26＋n ＝53，所以m ＝2.(2)由(1)知f (x )＝23⎝⎛⎭⎪⎫x ＋1x ，f (x )在区间(0,1]上是减函数，在区间[1，＋∞)上是增函数．证明如下：任取x1<x2，且x1，x2∈(0，＋∞)，那么f(x1)－f(x2)＝23⎝⎛⎭⎪⎫x1＋1x1－23⎝⎛⎭⎪⎫x2＋1x2＝2(x1－x2)(x1x2－1)3x1x2.当x1，x2∈(0,1]时，0<x1x2<1，∴x1x2－1<0，又x1<x2，∴x1－x2<0.∴f(x1)－f(x2)>0，即f(x1)>f(x2)，∴f(x)在区间(0,1]上是减函数；当x1，x2∈[1，＋∞)时，x1x2>1，∴x1x2－1>0，又x1<x2，∴x1－x2<0.∴f(x1)－f(x2)<0，即f(x1)<f(x2)，∴f(x)在区间[1，＋∞)上是增函数．。

第三章单元质量测评(二)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，满分150分，考试时间120分钟．第Ⅰ卷(选择题，共60分)一、选择题(本大题共12小题，每小题5分，共60分)1．[2016·银川一中月考]函数f(x)＝x2－2x的零点个数是( )A．0个B．1个C．2个D．3个答案 D解析画出y＝x2与y＝2x的图象，不难知道函数在(－∞，0)上有一个零点，另外x＝2，x＝4也是函数的零点，故函数f(x)零点的个数是3.2．[2015·荆州中学高一期中]实数a，b，c是图象连续不断的函数y＝f(x)定义域中的三个数，且满足a＜b＜c，f(a)f(b)＜0，f(c)f(b)＜0，则y＝f(x)在区间(a，c)的零点个数为( )A．2 B．奇数C．偶数D．至少是2答案 D解析因为f(a)f(b)＜0，所以在区间(a，b)上至少存在一个零点，同理在区间(b，c)上也至少存在一个零点，又因为(a，b)、(b，c)⊆(a，c)，故正确答案是D.3．[2016·辽宁鞍山一中期中]函数y＝2－|x|－m的图象与x轴有交点，则m 的取值范围是( )A ．[－1,0)B ．[0,1]C ．[1，＋∞)D ．(0,1]答案 D解析 解法一：函数y ＝2－|x|－m 的图象与x 轴有交点等价于函数y ＝2－|x|与y ＝m 的图象有交点，在同一坐标系中作出函数y ＝2－|x|，y ＝m 的图象，易知m ∈(0,1]．解法二：函数y ＝2－|x|－m 的图象与x 轴有交点，即关于x 的方程2－|x|＝m 有解，所以m 的取值范围是函数y ＝2－|x|的值域，所以m ∈(0,1]，故选D.4．[2016·海南中学高一期中]若方程x 3－x ＋1＝0在区间(a ，b)(其中a ，b 是整数，且b －a ＝1)上有一个根，则a ＋b 的值为( )A ．3B ．－5C ．－4D ．－3答案 D解析 设f(x)＝x 3－x ＋1， 则f(－2)＝－5，f(－1)＝1，可知f(x)在(－2，－1)上有零点，即方程x 3－x ＋1＝0在(－2，－1)上有根，所以a ＝－2，b ＝－1，a ＋b ＝－3.5．[2016·人大附中期末考试]设x 0是函数f(x)＝⎝ ⎛⎭⎪⎪⎫13x －log 2x 的零点，若0<a<x 0，则f(a)( )A ．等于0B ．小于0C ．大于0D ．不确定答案 C解析 ∵x 0是函数f(x)的零点，∴f(x 0)＝0.又函数f(x)＝⎝ ⎛⎭⎪⎪⎫13x －log 2x 在(0，＋∞)上单调递减，且0<a<x 0，∴f(a)>f(x 0)＝0，故选C.6．[2016·浙江温州中学期末]已知函数f(x)＝2x ＋x ，g(x)＝x ＋log 2x ，h(x)＝x 3＋x 的零点依次为a ，b ，c ，则a ，b ，c 的大小关系为( )A ．b>c>aB ．b>a>cC ．a>b>cD ．c>b>a答案 A解析 在同一坐标系中画出y ＝2x 和y ＝－x 的图象，可得a<0，用同样的方法可得b>0，c ＝0，所以b>c>a ，故选A.7．[2016·江西上饶中学期中]已知每生产100克饼干的原材料加工费为1.8元．某食品加工厂对饼干采用两种包装，包装费用、销售价格如表所示：则下列说法中正确的是( )①买小包装实惠；②买大包装实惠；③卖3小包比卖1大包盈利多；④卖1大包比卖3小包盈利多．A ．①③B ．①④C ．②③D ．②④。

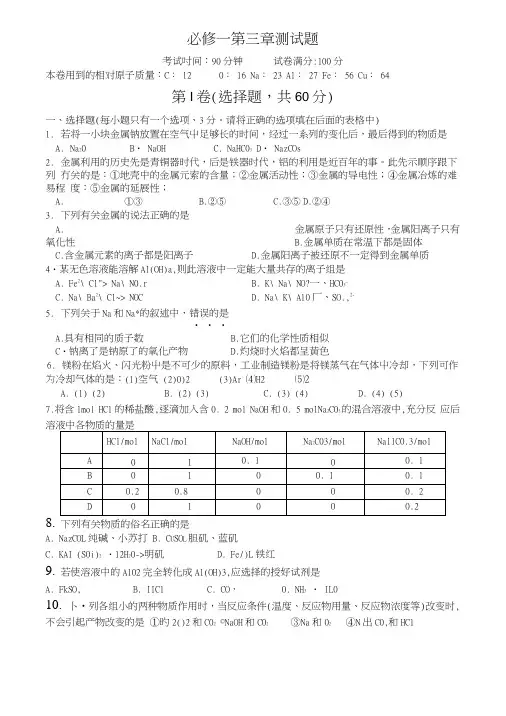
必修一第三章测试题考试吋间：90分钟试卷满分:100分本卷用到的相对原子质量：C： 12 0： 16 Na： 23 Al： 27 Fe： 56 Cu： 64第I卷(选择题，共60分)一、选择题(每小题只有一个选项、3分。

请将正确的选项填在后面的表格中)1.若将一小块金属钠放置在空气屮足够长的时间，经过一系列的变化后，最后得到的物质是A.Na20 B・ NaOH C. NaHC03 D・ NazCOs2.金属利用的历史先是青铜器时代，后是铁器时代，铝的利用是近百年的事。

此先示顺序跟下列冇关的是：①地壳中的金属元索的含量；②金属活动性；③金属的导电性；④金属冶炼的难易程度：⑤金属的延展性；A.①③B.②⑤C.③⑤D.②④3.下列有关金属的说法正确的是A.金属原子只有还原性，金属阳离子只有氧化性B.金属单质在常温下都是固体C.含金属元素的离子都是阳离子D.金属阳离子被还原不一定得到金属单质4・某无色溶液能溶解Al(OH)a,则此溶液中一定能大量共存的离子组是A. Fe2\ Cl"> Na\ N0.rB. K\ Na\ NO?一、HC03_C. Na\ Ba2\ Cl~> NOCD. Na\ K\ A10厂、SO.,2-5.下列关于Na和Na*的叙述中，错误的是• • •A.具有相同的质子数B.它们的化学性质相似C・钠离了是钠原了的氧化产物 D.灼烧时火焰都呈黄色6.镁粉在焰火、闪光粉屮是不可少的原料，工业制造镁粉是将镁蒸气在气体屮冷却，下列可作为冷却气体的是：(1)空气(2)0)2 (3)Ar ⑷H2 ⑸2A. (1) (2)B. (2) (3)C. (3) (4)D. (4) (5)7.将含lmol HC1的稀盐酸,逐滴加入含0. 2 mol NaOH和0. 5 molNa2C03的混合溶液中,充分反应后8.下列有关物质的俗名正确的是A. NazCOL纯碱、小苏打B. C U SO L胆矶、蓝矶C. KAI (S0i)2・12H20->明矶D. Fe/)L铁红9.若使溶液中的A102完全转化成A1(OH)3,应选择的授好试剂是A. FkSO,B. IIC1C. CO，0. NH3・ IL010.卜•列各组小的两种物质作用时，当反应条件(温度、反应物用量、反应物浓度等)改变时, 不会引起产物改变的是①旳2()2和C02©NaOH和C02③Na和02④N出C0,和HC1⑤A1CL 和NaOH @NaA102和CO2⑦Fe 和HC1⑧Ca (OHL 和NaHCO；,A.①⑥⑦⑧B. ®®C.①⑦D.①④⑦11・如下图所示，在蒸发皿中放一小块钠，加热至熔化时，用玻璃棒蘸取少虽无水CuSO.粉末与熔化的钠接触，瞬间产生耀眼的火花，同时有红色物质牛•成。

第一章集合与函数概念1．集合的相关概念(1)元素①定义：指的是研究对象．②表示：用小写的拉丁字母a，b，c，…表示．(2)集合①含义：指的是一些元素组成的总体．②表示：用大写的拉丁字母A，B，C，…表示．(3)集合相等：指构成两个集合的元素是一样的．(4)集合中元素的特性：确定性、互异性和无序性．2．元素与集合的关系(1)“属于”：如果a是集合A的元素，就说a属于集合A，记作a∈A.(2)“不属于”：如果a不是集合A的元素，就说a不属于集合A，记作a∉A. 3．常见的数集及表示符号集合的概念A．中央电视台著名节目主持人B．我市跑得快的汽车C．上海市所有的中学生D．香港的高楼答案 C解析 对A ，“著名”无明确标准；对B ，“快”的标准不确定；对D ，“高”的标准不确定，因而A 、B 、D 均不能组成集合．而对C ，上海市的中学生是确定的，能组成集合．2．已知a 和b 都是自然数，且a≠b ，由a ，b ，a 2，b 2，a 3，b 3构成的集合M 中，元素的个数最少为________．答案 2个解析 ⎩⎪⎨⎪⎧ a ＝0，b ＝1，或⎩⎪⎨⎪⎧a ＝1，b ＝0，则a ＝a 2＝a 3，b ＝b 2＝b 3， 此时元素的个数最少，只有2个.元素与集合的关系3.给出下列关系式：2∈R,0.3∈Q,0∉N,0∈N *，12∈N *，－π∉Z.其中正确的有( )A ．3个B ．4个C ．5个D ．6个答案 A解析 正确的有2∈R,0.3∈Q ，－π∉Z.4．已知集合A 中只有一个元素a ，则下列各式中正确的是( ) A ．0∈A B ．a ∉A C ．a ∈A D ．a ＝A 答案 C解析 集合A 中只有一个元素a ，所以a ∈A.集合中元素特性的应用5.解 若1∈A ，则a ＝1或a 2＝1，即a ＝±1. 当a ＝1时，a ＝a 2，集合A 有一个元素，∴a≠1. 当a ＝－1时，集合A 含有两个元素1，－1，符合互异性． ∴a ＝－1.忽视集合中元素的互异性致误6.易错分析 本题产生错误的原因是没有注意到字母a 的取值带有不确定性而得到错误答案两个元素．事实上，当a ＝1时，不满足集合中元素的互异性．正解 x 2－(a ＋1)x ＋a ＝(x －a)(x －1)＝0，所以方程的解为x 1＝1，x 2＝a.若a ＝1，则方程的解集中只含有一个元素1；若a≠1，则方程的解集中含有两个元素1，a.一、选择题1．下列各组对象中不能构成集合的是( ) A ．正三角形的全体 B ．所有的无理数C ．高一数学第一章的所有难题D ．不等式2x ＋3>1的解 答案 C解析 因为A 、B 、D 三项可以确定其元素，而C 中难题的标准无法确定．因此选C. 2．若a ∈R ，但a ∉Q ，则a 可以是( ) A ．3.14 B ．－5 C.37 D.7答案 D解析 由题意知a 是实数但不是有理数，故a 应为无理数． 3．下列三个结论： ①集合N 中最小的数是1， ②－a ∉N ，则a ∈N ，③a ∈N ，b ∈N ，则a ＋b 最小值是2. 其中正确结论的个数是( ) A ．0 B ．1 C ．2 D ．3 答案 A解析 因为自然数集中最小的数是0，而不是1，所以①错；对于②，取a ＝2，则－2∉N ，2∉N ，所以②错；对于③，a ＝0，b ＝0时，a ＋b 取得最小值0，而不是2，所以③错．4．[2016·衡水高一调研]若集合M 中的三个元素a 、b 、c 分别是△ABC 的三边长，则△ABC 一定不是( )A ．锐角三角形B ．直角三角形C ．钝角三角形D ．等腰三角形 答案 D解析 因为集合中元素具有互异性，所以a ，b ，c 互不相等，所以三角形不可能为等腰三角形，选D.5．[2016·泰安高一检测]下列所给关系正确的个数是( ) ①π∈R ；②3∉Q ；③0∈N *；④|－4|∉N *. A ．1 B ．2 C ．3 D ．4答案 B解析 π是实数，①对；3是无理数，②对；0不属于N *，③错；|－4|＝4,4∈N *，④错，故选B.二、填空题6．设直线y ＝2x ＋3上的点集为P ，点(2,7)与点集P 的关系为(2,7)________P(填“∈”或“∉”)．答案 ∈解析 直线y ＝2x ＋3上的点的横坐标x 和纵坐标y 具有y ＝2x ＋3的关系，即只要具备此关系的点就是集合P 的元素．由于当x ＝2时，y ＝2×2＋3＝7，故(2,7)∈P.7．设P ，Q 是两个数集，P 中含有0,2两个元素，Q 中含有1,2两个元素，定义集合P ＋Q 中的元素是a ＋b ，其中a ∈P ，b ∈Q ，则P ＋Q 中元素的个数是________．答案 4解析 由于a ∈P ，a ＝0或2，b ∈Q ，b ＝1或2，因此a ＋b 的值为1,2,3,4，共4个． 8．[2016·连云港高一检测]集合A 中的元素x 满足63－x∈N ，x ∈N ，则集合A 中的元素为________．答案 0,1,2解析 由题意知3－x 是6的正约数，当3－x ＝1时，x ＝2；当3－x ＝2时，x ＝1；当3－x ＝3时，x ＝0；当3－x ＝6时，x ＝－3；而x ∈N ，∴x ＝0,1,2，即集合A 中的元素为0,1,2.三、解答题9．判断下列说法是否正确，并说明理由． (1)某个单位里的年轻人组成一个集合；(2)由1，32，64，⎪⎪⎪⎪－12，12这些数组成的集合有五个元素； (3)由a ，b ，c 组成的集合与由b ，a ，c 组成的集合是相等的．解 (1)不正确．因为判断是不是“年轻人”没有明确的标准，对象不具有确定性，不能组成集合．(2)不正确．由集合的互异性可知，这个集合是由三个元素组成的．(3)正确．集合中的元素相同，只是次序不同，它们仍表示同一个集合．10．已知集合中含有三个元素：a＋2，(a＋1)2，a2＋3a＋3，且1∈A，求实数a的值．解∵1∈A，∴a＋2＝1或(a＋1)2＝1或a2＋3a＋3＝1.∴a＝－1或a＝0或a＝－2.当a＝－1时，集合中的元素为：a＋2＝1，(a＋1)2＝0，a2＋3a＋3＝1，不符合元素的互异性，舍去；当a＝0时，集合中的元素为：a＋2＝2，(a＋1)2＝1，a2＋3a＋3＝3，符合元素的互异性；当a＝－2时，集合A中的元素为：a＋2＝0，(a＋1)2＝1，a2＋3a＋3＝1，不符合元素的互异性，舍去．综上a＝0.课时2集合的表示1．列举法表示集合(1)定义：把集合的元素一一列举出来，并用花括号“{}”括起来表示集合的方法．(2)形式：A＝{a1，a2，a3，…，a n}．2．描述法表示集合(1)定义：用集合所含元素的共同特征表示集合的方法．(2)具体方法：在花括号内先写上表示这个集合元素的一般符号及取值(或变化)范围，再画一条竖线，在竖线后写出这个集合中元素所具有的共同特征.用列举法表示集合1.________答案{(－1,1)}解析因为(x＋1)2≥0，|y－1|≥0，所以(x＋1)2＝0且|y－1|＝0，故有x＝－1且y＝1，因此答案为{(－1,1)}．2．已知集合A＝{x|x<5且x∈N*}，B＝{(a，b)|a＋b2＝1，b∈A}，试用列举法表示集合B＝________.答案{(0,1)，(－3,2)，(－8,3)，(－15,4)}解析∵x∈N*，且x<5，∴x＝1,2,3,4，∴A＝{1,2,3,4}．又∵a＋b2＝1，且b∈A，∴当b ＝1时，a ＝0，当b ＝2时，a ＝－3， 当b ＝3时，a ＝－8，当b ＝4时，a ＝－15. ∴B ＝{(0,1)，(－3,2)，(－8,3)，(－15,4)}.用描述法表示集合3.集合A ．{x|x ＝2k ，k ∈Z} B ．{x|x ＝2k ，k ∈N} C ．{x|x ＝2k ，k ∈N *} D ．以上都不对答案 C解析 因为正偶数都能被2整除，因此选C.4．将集合“正奇数的全体”用描述法表示正确的是( ) A ．{x|x ＝2n ＋1，n ∈N *} B ．{x|x ＝2n －1，n ∈N *} C ．{x|x ＝2n －1，n ∈Z} D ．{x|x ＝2n ＋1，n ∈Z} 答案 B解析 A 项中没有1；C ，D 两项表示奇数集.集合表示法的应用 5.中只有一个元素，求解 应根据a 是否为0分两种情况进行讨论：①a ＝0，此时A ＝⎩⎨⎧⎭⎬⎫－12，符合题意；②a≠0，则必须且只需Δ＝4－4a ＝0，即a ＝1. ∴a ＝0或a ＝1.对描述法表示集合的理解不够而出错(1)A ＝{y|y ＝－x 2＋6，x ∈N ，y ∈N}； (2)B ＝{(x ，y)|y ＝－x 2＋6，x ∈N ，y ∈N}．易错分析 本题产生错误的原因是对用描述法表示的集合分不清其代表元素，导致用列举法表示集合时出现错误．正解 (1)因为y ＝－x 2＋6≤6，且x ∈N ，y ∈N ， 所以x ＝0,1,2时，y ＝6,5,2，符合题意， 所以A ＝{2,5,6}．(2)(x ，y)满足条件y ＝－x 2＋6，x ∈N ，y ∈N ，则有⎩⎪⎨⎪⎧ x ＝0y ＝6，⎩⎪⎨⎪⎧ x ＝1y ＝5，⎩⎪⎨⎪⎧x ＝2y ＝2，所以B ＝{(0,6)，(1,5)，(2,2)}.一、选择题1．方程组⎩⎪⎨⎪⎧x ＋y ＝3，x －y ＝1的解组成的集合是( )A ．{2,1}B ．(2,1)C ．{(2,1)}D ．{－1,2}答案 C解析 先求出方程组的解⎩⎪⎨⎪⎧x ＝2，y ＝1，再写成集合的形式．注意集合的元素是有序实数对(2,1)，故选C.2．用列举法可将集合{(x ，y)|x ∈{1,2}，y ∈{1,2}}表示为( ) A ．{1,2} B ．{(1,2)} C ．{(1,1)，(2,2)}D ．{(1,1)，(1,2)，(2,1)，(2,2)} 答案 D解析 x ＝1时，y ＝1,2；x ＝2时，y ＝1,2.共有4组，故选D.3．[2016·成都高一一诊]已知集合P ＝{1,2}，Q ＝{z|z ＝x ＋y ，x ，y ∈P}，则集合Q 为( ) A ．{1,2,3} B ．{2,3,4} C ．{3,4,5} D ．{2,3}答案 B解析 ∵1＋1＝2,1＋2＝3,2＋1＝3,2＋2＝4， 又集合中的元素具有互异性， ∴Q ＝{2,3,4}，故选B.4．[2016·成都七中高一月考]已知集合A ＝{1,2,3,4,5}，B ＝{(x ，y)|x ∈A ，y ∈A ，x －y ∈A}，则B 中的元素个数为( )A ．3B ．6C ．8D ．10 答案 D解析 ∵x ∈A ，y ∈A ，且x －y ∈A.∴x ＝2时，y ＝1；x ＝3时，y ＝2,1；x ＝4时，y ＝3,2,1；x ＝5时，y ＝4,3,2,1.所以集合B 中的元素共有1＋2＋3＋4＝10个，故选D.5．[2016·南昌高一检测]若1∈{x ，x 2}，则x ＝( )A．1 B．－1C．0或1 D．0或1或－1答案 B解析若x＝1则x2＝1不满足互异性，若x2＝1则x＝±1且x＝1舍去，故x＝－1.二、填空题6．[2016·汉中高一检测]若集合A＝{1,2,3,4}，集合B＝{y|y＝x－1，x∈A}，将集合B 用列举法表示为________．答案{0,1,2,3}解析当x＝1,2,3,4时，y＝x－1，∴y＝0,1,2,3，∴B＝{0,1,2,3}．7．[2016·昆明高一检测]设－5∈{x|x2－ax－5＝0}，则集合{x|x2－5x－a＝0}中所有元素之和为________．答案 5解析由－5∈{x|x2－ax－5＝0}得：25＋5a－5＝0，∴a＝－4，则集合{x|x2－5x－a＝0}＝{x|x2－5x＋4＝0}＝{x|(x－1)(x－4)＝0}＝{1,4}，∴集合中所有元素之和为1＋4＝5.8．集合A＝{m|m＋1≥5}，B＝{y|y＝x2＋2x＋5，x∈R}，则A、B________(填“是”或“否”)表示同一集合．答案是解析A＝{m|m≥4，m∈R}，即A中元素为大于或等于4的所有实数；B＝{y|y＝(x＋1)2＋4}，即y＝(x＋1)2＋4≥4，所以B中元素也为大于或等于4的所有实数，故A、B表示同一集合．三、解答题9．将大于0不大于15且除以4余3的整数构成的集合分别用列举法和描述法表示出来．解列举法：{3,7,11,15}；描述法：{x|0<x≤15，且x＝4n＋3，n∈N}．10．集合A＝{x|kx2－8x＋16＝0}，若集合A中只有一个元素，试求实数k的值，并用列举法表示集合A.解当k＝0时，原方程变为－8x＋16＝0，x＝2.此时集合A＝{2}．当k≠0时，要使一元二次方程kx2－8x＋16＝0有两个相等的实根，只需Δ＝64－64k＝0，即k＝1.此时方程的解为x1＝x2＝4，集合A＝{4}，满足题意．综上所述，实数k的值为0或1.当k＝0时，A＝{2}；当k＝1时，A＝{4}．►1.1.2集合间的基本关系课时3集合间的基本关系1．Venn图表示集合通常用平面上封闭曲线的内部表示一个集合．2．子集的有关概念(1)子集①定义：对于两个集合A，B，如果集合A中任意一个元素都是集合B中的元素，我们就说这两个集合有包含关系，称集合A为集合B的子集；②记作：A⊆B(或B⊇A)；③读作：“A包含于B”(或“B包含A”)．(2)集合相等①定义：如果集合A是集合B的子集(A⊆B)，且集合B是集合A的子集(B⊆A)，此时，集合A与集合B中的元素是一样的，因此集合A和集合B相等．②符合表示：若A⊆B且B⊆A，则A＝B.(3)真子集①定义：如果集合A⊆B，但存在元素x∈B，且x∉A，我们称集合A是集合B的真子集．②记法：A B(或B A)．③图示：3．空集(1)定义：不含任何元素的集合叫做空集，记为∅；(2)规定：空集是任何集合的子集．4．集合间关系的性质(1)任何一个集合都是它本身的子集，即A⊆A.(2)对于集合A，B，C，①若A⊆B，且B⊆C，则A⊆C；②若A B，B C，则A C.(3)若A⊆B，A≠B，则A B.子集的概念1.①空集没有子集；②空集是任何一个集合的真子集； ③∅＝{0}；④任何一个集合必有两个或两个以上的子集． 其中正确命题的个数为( ) A ．0个 B ．1个 C ．2个 D ．3个答案 A解析 空集是其本身的子集，是任何集合的子集，是任何非空集合的真子集． 2．写出A ＝{0,1,2}的所有子集，并指出其中哪些是集合A 的真子集．解 {0,1,2}的所有子集：∅，{0}，{1}，{2}，{0,1}，{0,2}，{1,2}，{0,1,2}，其中集合A 的真子集有：∅，{0}，{1}，{2}，{0,1}，{0,2}，{1,2}.3.之间的关系是A ．A B B ．A B C ．A ＝B D ．不能确定答案 A解析 B ＝{x|x<5}，利用数轴易知A B.4．[2016·福建六校高一联考]已知集合A ＝{0,1}，则下列式子错误的是( ) A ．0∈A B ．{1}∈A C ．∅⊆A D ．{0,1}⊆A 答案 B解析 “∈”用于元素与集合之间，而{1}是A 的子集， ∴应为{1}⊆A.集合相等问题5.设解 由P ＝Q 得⎩⎪⎨⎪⎧ a ＝2a ，b ＝b 2，①或⎩⎪⎨⎪⎧b ＝2a ，a ＝b 2.②解①得⎩⎪⎨⎪⎧ a ＝0，b ＝0，或⎩⎪⎨⎪⎧a ＝0，b ＝1.解②得⎩⎪⎨⎪⎧a ＝0，b ＝0，或⎩⎨⎧a ＝14，b ＝12.当a ＝b ＝0时，不符合元素的互异性，舍去． ∴a ＝0，b ＝1或a ＝14，b ＝12.6.，则实数． 易错分析 由集合B ⊆A 及B 的含义求a 时，易忽略B ＝∅时的情况，也就丢了a 的可能解．答案 0或23或－2正解 由A ＝{x|x 2－2x －3＝0}＝{－1,3}得 当B ⊆A 时，B ＝∅或B ＝{－1}或B ＝{3}， 当B ＝∅时，a ＝0.当B ＝{－1}时，得a ＝－2. 当B ＝{3}时，得a ＝23.综上可知：a ＝0或a ＝－2或a ＝23.一、选择题1．下列各式中，正确的是( ) A ．23∈{x|x≤3} B ．23∉{x|x≤3} C ．23⊆{x|x≤3} D ．{23} {x|x≤3} 答案 B解析 23表示一个元素，{x|x≤3}表示一个集合，但23不在集合中，故23∉{x|x≤3}，A ，C 不正确，又集合{23}{x|x≤3}，故D 不正确．2．[2016·成都七中高一月考]下列四个集合中，表示空集的是( ) A ．{0}B ．{(x ，y)|x 2＋y 2＝0，x ，y ∈R}C ．{x||x|＝5，x ∈Z ，x ∉N}D．{x|2x2＋3x－2＝0，x∈N}答案 D解析A中，{0}有元素0，不是空集；B中，集合为{(0,0)}，不是空集；C中，集合为{－5}，不是空集；D中，方程没有非负整数解，为空集，选D.3．[2016·福建漳州高一质检]定义集合A*B＝{x|x∈A，且x∉B}，若A＝{1,3,5,7}，B＝{2,3,5}，则A*B的子集个数为()A．1 B．2C．3 D．4答案 D解析A*B中的元素有{1,7}，∴A*B的子集个数为22＝4个，选D.4．集合B＝{a，b，c}，C＝{a，b，d}，集合A满足A⊆B，A⊆C，则集合A的个数是()A．8 B．3C．4 D．1答案 C解析若A＝∅，则满足A⊆B，A⊆C；若A≠∅，由A⊆B，A⊆C知A是由属于B且属于C的元素构成，此时集合A可能为{a}，{b}，{a，b}．5．[2016·浏阳高一检测]已知集合A＝{x|3≤x2≤5，x∈Z}，则集合A的真子集个数为() A．1个B．2个C．3个D．4个答案 C解析A＝{x|3≤x2≤5}＝{2，－2}，它的真子集有∅，{2}，{－2}，共3个．二、填空题6．已知集合U，S，T，F之间的关系如下图所示，下列关系中错误的有________．(只填序号)①S U；②F T；③S T；④S F；⑤S F；⑥F U.答案②④⑤解析根据子集、真子集的Venn图，可知S U，S T，F U正确，其余错误．7．[2016·玉溪高一检测]已知集合A ＝{x|－2≤x≤3}，B ＝{x|x≥m}，若A ⊆B ，则实数m 的取值范围为________．答案 m≤－2解析 由已知A ⊆B ，画数轴可得m≤－2.8．设x ，y ∈R ，A ＝{(x ，y)|y ＝x}，B ＝⎩⎨⎧⎭⎬⎫ x ，y ⎪⎪y x ＝1，则A ，B 的关系是________．答案 B A解析 A 中(x ，y)，x ∈R ，y ∈R ，所以A 表示直线y ＝x 上所有点构成的集合． B 中的x≠0，所以B 表示直线y ＝x 上所有点构成的集合，但除去原点． ∴B A. 三、解答题9．设集合A ＝{1，－2，a 2－1}，B ＝{1，a 2－3a,0}．若A ＝B ，求a 的值． 解 由A ＝B 及集合中元素特点可得⎩⎪⎨⎪⎧ a 2－1＝0，a 2－3a ＝－2，解得⎩⎪⎨⎪⎧a ＝±1，a ＝1或a ＝2，∴a ＝1. 把a ＝1代入验证，满足集合中元素的互异性． ∴a ＝1.10．若集合M ＝{x|x 2＋x －6＝0}，N ＝{x|(x －2)(x －a)＝0}，且N ⊆M ，求实数a 的值． 解 由x 2＋x －6＝0，得x ＝2或x ＝－3. 所以M ＝{2，－3}．若a ＝2，则N ＝{2}，此时N M ； 若a ＝－3，则N ＝{2，－3}，此时N ＝M ；若a≠2且a≠－3，则N ＝{2，a}，此时N 不是M 的子集，故所求实数a 的值为2或－3.►1.1.3 集合的基本运算 课时4 并集、交集1．并集(1)定义：一般地，由所有属于集合A 或属于集合B 的元素组成的集合，称为集合A 与B的并集，记作A∪B.(2)并集的符号语言表示为A∪B＝{x|x∈A，或x∈B}．(3)性质：A∪B＝B∪A，A∪A＝A，A∪∅＝A，A∪B＝A⇔B⊆A，A⊆A∪B.2．交集(1)定义：一般地，由属于集合A且属于集合B的所有元素组成的集合，称为A与B的交集，记作A∩B.(2)交集的符号语言表示为A∩B＝{x|x∈A，且x∈B}．(3)性质：A∩B＝B∩A，A∩A＝A，A∩∅＝∅，A∩B＝A⇔A⊆B，A∩B⊆A∪B，A∩B⊆A，A∩B⊆B.并集的运算1.A．{2,3,4,5,6} B．{1,2,3,4,5,6}C．{1,2,3,4,5} D．{2,3,4,5}答案 B解析∵M＝{2,3,4,5}，∴P∪M＝{1,2,3,4,5,6}．2．已知集合M＝{x|－3<x≤5}，N＝{x|x<－5或x>5}，则M∪N＝()A．{x|x<－5或x>－3} B．{x|－5<x<5}C．{x|－3<x<5} D．{x|x<－3或x>5}答案 A解析由题意画出数轴．可知，M∪N＝{x|x<－5或x>－3}．交集的运算3.)A．{0} B．{－1,0}C．{0,1} D．{－1,0,1}答案 B解析∵－1,0∈B,1∉B，∴A∩B＝{－1,0}．4．设A ＝{x|－1<x<2}，B ＝{x|x<a}，若A∩B≠∅，则a 的取值范围是________． 答案 a>－1解析 结合数轴可知a>－1.并集、交集运算的应用5.的值．解 ∵A∩B ＝B ，∴B ⊆A. ∵A ＝{－2}≠∅，∴B ＝∅或B≠∅.当B ＝∅时，方程ax ＋1＝0无解，此时a ＝0.当B≠∅时，此时a≠0，则B ＝⎩⎨⎧⎭⎬⎫－1a ，∴－1a ∈A ，即有－1a ＝－2，得a ＝12.综上，a ＝0或a ＝12.6.集合A ，若A∩B a 的取值范围是________．易错分析 本题由A∩B ＝B 得B ⊆A ，则B ＝{1}或B ＝{2}或B ＝{1,2}，忽视了B ＝∅的可能性，从而导致a 的取值范围错误．答案 {a|a≥2}正解 由题意得A ＝{1,2}，∵A∩B ＝B ，∴B ⊆A ，∴B ＝∅或B ＝{1}或B ＝{2}或B ＝{1,2}． 当B ＝∅时，Δ＝4－4(a －1)<0，得a>2.当B ＝{1}时，⎩⎪⎨⎪⎧12－2×1＋a －1＝0Δ＝4－4 a －1 ＝0，得a ＝2. 当B ＝{2}时，⎩⎪⎨⎪⎧22－4＋a －1＝0Δ＝4－4 a －1 ＝0，无解．当B ＝{1,2}时，此时a 无解． 综上可知，a 的取值范围是{a|a≥2}.一、选择题1．若集合A ＝{0,1,2,3}，B ＝{1,2,4}，则集合A ∪B ＝( ) A ．{0,1,2,3,4} B ．{1,2,3,4} C ．{1,2} D ．{0}答案 A解析 由并集的概念，可得A ∪B ＝{0,1,2,3,4}．2．已知集合M ＝{(x ，y)|x ＋y ＝2}，N ＝{(x ，y)|x －y ＝4}，那么集合M∩N 为( ) A ．x ＝3，y ＝－1 B ．(3，－1) C ．{3，－1} D ．{(3，－1)}答案 D解析 ∵要求集合M 与N 的公共元素，∴⎩⎪⎨⎪⎧ x ＋y ＝2x －y ＝4解得⎩⎪⎨⎪⎧x ＝3y ＝－1∴M∩N ＝{(3，－1)}，选D.3．设全集U ＝R ，A ＝{x ∈N|1≤x≤10}，B ＝{x ∈R|x 2＋x －6＝0}，则右图中阴影部分表示的集合为( )A ．{2}B ．{3}C ．{－3,2}D ．{－2,3}答案 A解析 注意到集合A 中的元素为自然数，因此易知A ＝{1,2,3,4,5,6,7,8,9,10}，而直接解集合B 中的方程可知B ＝{－3,2}，因此阴影部分显然表示的是A∩B ＝{2}，选A.4．满足M ⊆{a 1，a 2，a 3，a 4}，且M∩{a 1，a 2，a 3}＝{a 1，a 2}的集合M 的个数是( ) A ．1 B ．2 C ．3 D ．4 答案 B解析 直接列出满足条件的M 集合有{a 1，a 2}、{a 1，a 2，a 4}，因此选B. 5．集合A ＝{x|－1≤x≤2}，B ＝{x|x<1}，则A∩B 等于( )A ．{x|x<1}B ．{x|－1≤x≤2}C ．{x|－1≤x≤1}D ．{x|－1≤x<1}答案 D解析 由交集定义得{x|－1≤x≤2}∩{x|x<1}＝{x|－1≤x<1}． 二、填空题6．[2015·江苏高考]已知集合A ＝{1,2,3}，B ＝{2,4,5}，则集合A ∪B 中元素的个数为________．答案 5解析 A ∪B ＝{1,2,3,4,5}，∴A ∪B 中元素的个数为5. 7．[2016·福建六校高一联考]已知集合A ＝{1,3，m}， B ＝{3,4}，A ∪B ＝{1,2,3,4}，则m ＝________. 答案 2解析 由题意易知2∈(A ∪B)，且2∉B ，∴2∈A ，∴m ＝2.8．已知集合P ＝{－1，a ＋b ，ab}，集合Q ＝⎩⎨⎧⎭⎬⎫0，b a ，a －b ，若P ∪Q ＝P∩Q ，则a －b＝________.答案 －4解析 由P ∪Q ＝P∩Q 易知P ＝Q ，由Q 集合可知a 和b 均不为0，因此ab≠0，于是必须a ＋b ＝0，所以易得ba ＝－1，因此又必得ab ＝a －b ，代入b ＝－a 解得a ＝－2.所以b ＝2，因此得到a －b ＝－4.三、解答题9．[2016·山东烟台模块检测]已知集合A ＝{x|a≤x≤a ＋3}，B ＝{x|x<－1或x>5}． (1)若A∩B ＝∅，求a 的取值范围； (2)若A ∪B ＝B ，求a 的取值范围． 解 (1)要使A∩B ＝∅，则需满足下列不等式组⎩⎪⎨⎪⎧a ＋3≤5，a≥－1，解此不等式组得－1≤a≤2， 即a 的取值范围是{a|－1≤a≤2}． (2)要使A ∪B ＝B ，即A 是B 的子集， 则需满足a ＋3<－1或a>5， 解得a>5或a<－4，即a 的取值范围是{a|a>5或a<－4}．10．[2016·衡水高一调研]已知集合A ＝{－1,1}，B ＝{x|x 2－2ax ＋b ＝0}，若B≠∅且A ∪B ＝A ，求a ，b 的值．解 B≠∅且A ∪B ＝A ，所以B≠∅且B ⊆A ，故B 存在两种情况： (1)当B 含有两个元素时，B ＝A ＝{－1,1}，此时a ＝0，b ＝－1； (2)当B 含有一个元素时，Δ＝4a 2－4b ＝0，∴a 2＝b. 若B ＝{1}时，有a 2－2a ＋1＝0，∴a ＝1，b ＝1. 若B ＝{－1}时，有a 2＋2a ＋1＝0，∴a ＝－1，b ＝1.综上：⎩⎪⎨⎪⎧ a ＝0，b ＝－1或⎩⎪⎨⎪⎧ a ＝1，b ＝1或⎩⎪⎨⎪⎧a ＝－1，b ＝1.课时5 补集1．全集(1)定义：如果一个集合含有我们所研究问题中涉及的所有元素，那么就称这个集合为全集．(2)记法：全集通常记作U. 2．补集∁U U ＝∅，∁U ∅＝U ，∁U (∁U A)＝A . A∩(∁U A)＝∅. ∁U (A∩B)＝(∁U A)∪(∁U B)． ∁U (A ∪B)＝(∁U A)∩(∁U B).补集的简单运算1.若U U 等于A ．∅ B ．{1,3} C ．{4}D ．{2,5}答案 A解析 由题意可知：∁U A ＝{2,5}，∁U B ＝{1,3}． ∴(∁U A)∩(∁U B)＝∅，选A.2．[2015·浙江高考]设全集U ＝{x ∈N|x≥2}，集合A ＝{x ∈N|x 2≥5}，则∁U A ＝( ) A ．∅ B ．{2} C ．{5} D ．{2,5}答案 B解析 A ＝{x ∈N|x 2≥5}＝{x ∈N|x≥3}，U ＝{x ∈N|x≥2}，∴∁U A ＝{2}，故选B.补集的应用3.答案 A∩(∁U B)解析 由韦恩图可知阴影部分位于集合A 内，但不位于集合B 内，∴阴影部分表示的集合为A∩(∁U B)．4．[2015·上海高考]设全集U ＝R.若集合A ＝{1,2,3,4}，B ＝{x|2≤x≤3}，则A∩(∁U B)＝________.答案 {1,4}解析 ∁U B ＝{x|x<2或x>3}，A ＝{1,2,3,4}， ∴A∩(∁U B)＝{1,4}．5．已知集合A ＝{x|x 2＋ax ＋12b ＝0}和B ＝{x|x 2－ax ＋b ＝0}，满足(∁U A)∩B ＝{2}，A∩(∁U B)＝{4}，U ＝R ，求实数a ，b 的值．解 ∵(∁U A)∩B ＝{2}，∴2∈B ，∴4－2a ＋b ＝0.① 又∵A∩(∁U B)＝{4}，∴4∈A ，∴16＋4a ＋12b ＝0.②联立①②，得⎩⎪⎨⎪⎧4－2a ＋b ＝0，16＋4a ＋12b ＝0，解得⎩⎨⎧a ＝87，b ＝－127.6.U M)∩N易错分析本题易产生的错解是在进行集合的交集运算时，遗漏了0这个端点值．由于集合变成了单元素集，所以常常会出现遗漏的情况．答案{x|x≥2或x＝0}正解N＝{y|y＝x2}＝{x|x≥0}，∁U M＝{x|x≤0或x≥2}，则(∁U M)∩N＝{x|x≥2或x＝0}．一、选择题1．设全集U＝{a，b，c，d}，集合M＝{a，c，d}，N＝{b，d}，则(∁U M)∩N等于() A．{b} B．{d}C．{a，c} D．{b，d}答案 A解析由题意可知，∁U M＝{b}，∴(∁U M)∩N＝{b}，选A.2．设全集U＝M∪N＝{1,2,3,4,5}，M∩(∁U N)＝{2,4}，则N等于()A．{1,2,3} B．{1,3,5}C．{1,4,5} D．{2,3,4}答案 B解析∵M∩(∁U N)＝{2,4}，∴2,4∈M且2,4∉N，又∵M∪N＝{1,2,3,4,5}，∴N＝{1,3,5}，选B.3．[2016·杭州七校高一联考]已知全集U＝{－1,1,3}，集合A＝{a＋2，a2＋2}，且∁U A ＝{－1}，则a的值是()A．－1 B．1C．3 D．±1答案 A解析由A∪(∁U A)＝U，可知A＝{1,3}，又∵a2＋2≥2，∴a＋2＝1且a2＋2＝3.解得a＝－1，故选A.4．如下图，U是全集，M，P，S是U的三个子集，则阴影部分所表示的集合是()A．(M∩P)∩S B．(M∩P)∪SC．(M∩P)∩(∁U S) D．(M∩P)∪(∁U S)答案 C解析由题图不难判断阴影部分位于M∩P中，但不在S中，故阴影部分表示的集合为(M∩P)∩(∁U S)，选C.5．[2016·哈尔滨九中期末]已知全集U＝{1,2,3,4,5,6,7}，M＝{3,4,5}，N＝{1,3,6}，则集合{2,7}等于()A．M∩N B．(∁U M)∩(∁U N)C．(∁U M)∪(∁U N) D．M∪N答案 B解析根据元素与集合的关系和集合的运算规律可知，2,7既不在集合M中，也不在集合N中，所以2,7在集合∁U M且在∁U N中，根据交集的意义即可知{2,7}＝(∁U M)∩(∁U N)．二、填空题6．有15人进入家电超市，其中有9人买了电视机，有7人买了电脑，两种均买的有3人，则这两种均没买的有________人．答案 2解析设这15人构成全集U，买电视机的9人构成集合A，买电脑的7人构成集合B，用Venn图表示，如图所示，则两种均没买的有15－(9－3)－3－(7－3)＝2(人)．7．已知集合A＝{x|x＜a}，B＝{x|1＜x＜2}，A∪(∁R B)＝R，则实数a的取值范围是________．答案 {a|a≥2}解析 ∵∁R B ＝{x|x≤1或x≥2}，又A ＝{x|x ＜a}，且A ∪(∁R B)＝R ，∴a≥2. 8．已知集合U ＝{(x ，y)|y ＝3(x －1)＋2}，A ＝{ (x ，y)|⎭⎬⎫y －2x －1＝3，则∁U A ＝________. 答案 {(1,2)}解析 ∵A ＝{(x ，y)|y ＝3(x －1)＋2，x≠1}．又当x ＝1时，由y ＝3(x －1)＋2得y ＝2，∴∁U A ＝{(1,2)}．三、解答题9．[2016·郑州期末]已知集合A ＝{x|0<2x ＋a≤3}，B ＝⎩⎨⎧⎭⎬⎫x ⎪⎪－12<x<2. (1)当a ＝1时，求A ∪(∁R B)； (2)若A ⊆B ，求实数a 的取值范围． 解 (1)当a ＝1时，A ＝⎩⎨⎧x ⎪⎪⎭⎬⎫－12<x≤1， ∁R B ＝⎩⎨⎧x ⎪⎪⎭⎬⎫x≤－12或x≥2， ∴A ∪(∁R B)＝{x|x≤1或x≥2}．(2)A ＝⎩⎨⎧x ⎪⎪⎭⎬⎫－a2<x≤3－a 2， 若A ⊆B ，则⎩⎨⎧－a 2≥－12，3－a2<2，解得－1<a≤1，所以a 的取值范围是{a|－1<a≤1}．10．已知集合U ＝{1,2,3,4,5,6,7,8,9,10}，A ＝{1,2,3,4,5,6}，B ＝{5,6,7,8,9,10}． (1)求(∁U A)∩(∁U B)，∁U (A ∪B)，(∁U A)∪(∁U B)，∁U (A∩B)； (2)从(1)的计算结果，能发现什么规律？解 (1)(∁U A)∩(∁U B)＝{7,8,9,10}∩{1,2,3,4}＝∅，∁U (A ∪B)＝∅，(∁U A)∪(∁U B)＝{7,8,9,10}∪{1,2,3,4}＝{1,2,3,4,7,8,9,10}，∁U (A∩B)＝{1,2,3,4,7,8,9,10}．(2)(∁U A)∩(∁U B)＝∁U (A ∪B)， (∁U A)∪(∁U B)＝∁U (A∩B)．习题课(1)复习要点集合是数学中最基本的概念，学习时一是要注意把集合知识作为一种语言来学习，集合语言是用集合的有关概念和符号来描述问题的语言，能简洁、准确地表达相关的数学内容；二是要注意集合中元素的互异性及空集的特殊性；三是要注意使用集合间的运算法则或运算思想，解决一些逻辑关系较复杂的问题，例如运用补集思想解决问题等．提升训练一、选择题1．下列各项中，不能组成集合的是()A．所有三角形B．数学《必修1》中的所有习题C．所有有理数D．数学《必修1》中的所有难题答案 D解析因A、B、C三项可以确定其元素，而D中难题的标准无法确定，因此选D.2．设集合A＝{x|x≤13}，a＝11，那么()A．a A B．a∉AC．{a}∈A D．{a} A答案 D解析因a＝11＜13，∴{11} {x|x≤13}，∴选D.3．设集合A＝{x|1<x<4}，集合B＝{x|－1≤x≤3}，则A∩(∁R B)等于()A．{x|1<x<4} B．{x|3<x<4}C．{x|1<x<3} D．{x|1<x<2或3<x<4}答案 B解析∵B＝{x|－1≤x≤3}，则∁R B＝{x|x<－1或x>3}，∴A∩(∁R B)＝{x|3<x<4}．4.已知全集U＝R，集合A＝{1,2,3,4,5}，B＝{x∈R|x≥3}，右图中阴影部分所表示的集合为()A．{1} B．{1,2}C．{1,2,3} D．{0,1,2}答案 B解析由题意得，A∩B＝{3,4,5}，阴影部分所表示的集合为集合A去掉集合A∩B中的元素所组成的集合，所以为{1,2}．5．50名学生参加甲、乙两项体育活动，每人至少参加了一项，参加甲项的学生有30名，参加乙项的学生有25名，则仅参加了一项活动的学生人数为( )A ．50B ．45C ．40D ．35答案 B解析 记参加甲、乙项体育活动的学生组成的集合分别为A 、B ，则依题意有card(A ∪B)＝50，card(A)＝30，card(B)＝25，card(A∩B)＝30＋25－50＝5，于是只参加了一项活动的学生人数是(30－5)＋(25－5)＝45.(也可利用Venn 图解决问题)6．[2016·洛阳高一检测]已知全集U ＝{x|0<x<8，且x ∈Z}，集合A ，B 均为全集U 的子集，若∁U (A ∪B)＝{1,2,3}，(∁U A)∩B ＝{6,7}，则集合A 为( )A ．{1,2,3,4,5}B ．{4,5}C ．{4,5,6,7}D ．{1,2,3,6,7} 答案 B解析 U ＝{1,2,3,4,5,6,7}，如图：由图可知，∁U A ＝{1,2,3,6,7}，∴A ＝{4,5}，选B. 二、填空题7．[2016·邯郸高一检测]已知集合M ＝{(x ，y)|x ＋y ＝2}，N ＝{(x ，y)|x －y ＝4}，那么M∩N ＝________.答案 {(3，－1)}解析 ⎩⎪⎨⎪⎧x ＋y ＝2x －y ＝4，解得x ＝3，y ＝－1，即{(3，－1)}．8．定义A －B ＝{x|x ∈A 且x ∉B}，若M ＝{1,2,3,4,5}，N ＝{2,3,6}，则N －M ＝________. 答案 {6}解析 关键是理解A －B 运算的法则， N －M ＝{x|x ∈N ，且x ∉M}＝{6}．9．[2016·湖南省长沙一中月考]已知集合A ＝{－2,1,2}，B ＝{a ＋1，a}，且B ⊆A ，则实数a 的值是______．答案 1解析 由题意知a≥0，又B ⊆A ，所以⎩⎨⎧ a ＋1＝1a ＝2或⎩⎨⎧a ＋1＝2a ＝1，解得a ＝1.三、解答题10．[2015·山西太原五中期中]已知集合A ＝{a 2，a ＋1，－3}，B ＝{a －3,2a －1，a 2＋1}，若A∩B ＝{－3}，求实数a 的值．解 ∵A∩B ＝{－3}，∴－3∈B ，又a 2＋1≠－3，∴a －3＝－3或2a －1＝－3， ∴a ＝0或a ＝－1.当a ＝0时，A ＝{0,1，－3}，B ＝{－3，－1,1}，A∩B ＝{－3,1}，不合题意． 当a ＝－1时，A ＝{1,0，－3}，B ＝{－4，－3,2}，A∩B ＝{－3}，满足题意． 综上可知a 的值为－1.11．已知集合A ＝{x|ax 2＋2x ＋1＝0，a ∈R}至多有一个真子集，求a 的取值范围． 解 若A ＝∅，则集合A 无真子集，这时关于x 的方程ax 2＋2x ＋1＝0无实数解，则a≠0，且Δ＝4－4a<0，得a>1；若集合A 恰有一个真子集，这时集合A 必为单元素集，可分为两种情况： ①a ＝0时，方程为2x ＋1＝0，x ＝－12；②a≠0时，则Δ＝4－4a ＝0，a ＝1.综上，当集合A 至多有一个真子集时，实数a 的取值范围为{a|a≥1或a ＝0}．12．[2016·许昌五校高一联考]已知集合A ＝{x|x 2－3x ＋2＝0}，B ＝{x|x 2－ax ＋a －1＝0}，若A ∪B ＝A ，求实数a 的值．解 依题意得A ＝{x|x 2－3x ＋2＝0}＝{1,2}．因为A ∪B ＝A ，所以B ⊆A ，所以集合B 可分为{1,2}，{1}，{2}，或∅.①当B ＝{1,2}＝A 时，有⎩⎪⎨⎪⎧a ＝1＋2a －1＝1×2，所以a ＝3符合题意；②当B ＝{1}时，有⎩⎪⎨⎪⎧Δ＝a 2－4 a －1 ＝01－a ＋ a －1 ＝0，所以a ＝2符合题意； ③当B ＝{2}时，有⎩⎪⎨⎪⎧Δ＝a 2－4 a－1 ＝022－2a ＋ a －1 ＝0，无解；④当B ＝∅时，即方程x 2－ax ＋(a －1)＝0无实根， 所以Δ＝a 2－4(a －1)<0⇒(a －2)2<0，无解． 综上，a ＝2或a ＝3.课时6函数的概念1．函数的有关概念(1)定义①前提条件：给定的两个集合A，B为非空数集．②对应关系：A中的任何一个数x对应B中唯一确定的数f(x)．即：一一对应或多一对应．③结论：f：A→B称为从集合A到集合B的一个函数．(2)函数的记法集合A上的函数可记作：f：A→B或y＝f(x)，x∈A.2．区间及有关概念函数的概念1.A．y等于f与x的乘积B．f(x)一定是一个式子C．y是x的函数D．对于不同的x，y也不同答案 C解析符号y＝f(x)，即“y是x的函数”的数学表示，它仅仅是函数符号，不是表示“y 等于f与x的乘积”，f(x)也不一定是解析式，可以是图象、表格，也可以是文字叙述，故A、B错误；当y＝x2时，x＝1或x＝－1时，y＝1，故D错误．2．[2016·北师大附中月考]下列图形中不是函数的图象的是()答案 B解析对于图B，取x＝1，由图可知有2个y值与之对应，故B中图象不是函数图象.函数值问题等于A.1C．4 D．5答案 B解析由题可知，f(1)＝4，∴f[f(1)]＝f(4)＝2，故选B.4．已知f(x)＝x2＋1，g(x)＝3x＋2.则f[g(x)]＝__________.答案9x2＋12x＋5解析因为f(x)＝x2＋1，g(x)＝3x＋2，所以f[g(x)]＝(3x＋2)2＋1＝9x2＋12x＋5.区间的表示5.(1){x|x≥2或x<1}；(2){x|x ＝1或2<x≤3}； (3){x|2x －1≥0}．解 (1){x|x≥2或x<1}＝(－∞，1)∪[2，＋∞)． (2){x|x ＝1或2<x≤3}＝{1}∪(2,3]．(3){x|2x －1≥0}＝⎩⎨⎧⎭⎬⎫x ⎪⎪x≥12＝⎣⎡⎭⎫12，＋∞. 先化简再判断致误6.A ．y ＝x ＋1与y ＝x 2－1x －1B ．y ＝x 2＋1与s ＝t 2＋1C ．y ＝2x 与y ＝2x(x≥0)D ．y ＝(x ＋1)2与y ＝x 2易错分析 y ＝x 2－1x －1＝ x ＋1 x －1x －1＝x ＋1，可知A 中两函数相同为相等函数，该题容易先将解析式化简，然后再判断导致错误．答案 B正解 对于选项A ，前者定义域为R ，后者定义域为{x|x≠1}，不是相等函数；对于选项B ，虽然变量不同，但定义域与对应关系相同，是相等函数；对于选项C ，因为定义域不同，所以不是相等函数；对于选项D ，虽然定义域相同，但对应关系不同，不是相等函数.一、选择题1．设f(x)＝x 2－1x 2＋1，则f 2f ⎝⎛⎭⎫12＝( )A ．1B ．－1 C.53 D ．－35答案 B解析 f 2 f ⎝⎛⎭⎫12＝22－122＋1⎝⎛⎭⎫122－1⎝⎛⎭⎫122＋1＝35－3454＝35×⎝⎛⎭⎫－53＝－1. 2．[2016·太原五中高一月考]设M ＝{x|0≤x≤2}，N ＝{y|0≤y≤2}，给出下列四个图形，其中能表示从集合M到集合N的函数关系的有()答案 B解析A中x的取值为0≤x≤1，不符合；C中y的取值为0≤y≤3，不符合；D中，当x>0时，一个x存在两个y与之对应，不是函数，故选B.3．下列函数中，不满足f(2x)＝2f(x)的是()A．f(x)＝|x| B．f(x)＝x－|x|C．f(x)＝x＋1 D．f(x)＝－x答案 C解析将f(2x)表示出来，看与2f(x)是否相等．对于A，f(2x)＝|2x|＝2|x|＝2f(x)；对于B，f(2x)＝2x－|2x|＝2(x－|x|)＝2f(x)；对于C，f(2x)＝2x＋1≠2f(x)；对于D，f(2x)＝－2x＝2f(x)，故只有C不满足f(2x)＝2f(x)，所以选C.4．[2015·许昌五校高一联考]下列各组函数中表示同一函数的是()①f(x)＝－2x3与g(x)＝x－2x；②f(x)＝|x|与g(x)＝3x3；③f(x)＝x0与g(x)＝1x0；④f(x)＝x2－2x－1与g(t)＝t2－2t－1.A．①②B．②③C．③④D．①④答案 C解析①中，两函数定义域相同，都是(－∞，0]，但f(x)＝－2x3＝－x－2x与g(x)对应关系不同，不是同一函数；②中，两函数定义域相同，都是R，但g(x)＝3x3＝x与f(x)对应关系不同，不是同一函数；③中，定义域相同，对应关系也相同；④中虽然表示自变量的字母不相同，但两函数的定义域和对应关系都相同．故选C.5．[2016·西安高一检测]下列式子中不能表示函数y＝f(x)的是()A．x＝y2B．y＝x＋1C．x＋y＝0 D．y＝x2答案 A解析 根据函数的定义判断，由于A 中对于一个确定的x ，有2个y 与它对应，所以不符合函数的定义要求，故选A.二、填空题6．已知f(x)＝π(x ∈R)，则f(x 2)＝________. 答案 π解析 由函数的定义可知，f(x 2)＝π.7．若[a,3a －1]为一确定区间，则a 的取值范围是________． 答案 ⎝⎛⎭⎫12，＋∞解析 3a －1>a 则a>12，故a 的取值范围是⎝⎛⎭⎫12，＋∞. 8．已知函数f(x)的定义域为(0，＋∞)，且满足f(2)＝1，f(xy)＝f(x)＋f(y)，则f(1)＝________，f(4)＝________.答案 0 2解析 f(xy)＝f(x)＋f(y)，∴f(2)＝f(2×1)＝f(2)＋f(1)，∴f(1)＝0. 又∵f(4)＝f(2×2)＝f(2)＋f(2)＝2f(2)＝2. 三、解答题9．判断下列各组的两个函数是否相等，并说明理由． (1)y ＝x －1，x ∈R 与y ＝x －1，x ∈N ； (2)y ＝x 2与y ＝x·x ； (3)y ＝1＋1x 与y ＝1＋1u.解 (1)前者的定义域是R ，后者的定义域是N ，由于它们的定义域不同，故两个函数不相等．(2)前者的定义域是R ，后者的定义域是{x|x≥0}，它们的定义域不同，故两个函数不相等．(3)两个函数的定义域相同(均为非零实数)，对应关系相同(都是自变量取倒数后加1)，故两个函数相等．10．已知f(x)＝x 21＋x 2，x ∈R.(1)计算f(a)＋f ⎝⎛⎭⎫1a 的值；(2)计算f(1)＋f(2)＋f ⎝⎛⎭⎫12＋f(3)＋f ⎝⎛⎭⎫13＋f(4)＋f ⎝⎛⎭⎫14的值．解 (1)由于f(a)＝a 21＋a 2，f ⎝⎛⎫1a ＝11＋a 2，所以f(a)＋f ⎝⎛⎭⎫1a ＝1. (2)解法一：因为f(1)＝121＋12＝12，f(2)＝221＋22＝45， f ⎝⎛⎭⎫12＝⎝⎛⎭⎫1221＋⎝⎛⎭⎫122＝15，f(3)＝321＋32＝910， f ⎝⎛⎭⎫13＝⎝⎛⎭⎫1321＋⎝⎛⎭⎫132＝110，f(4)＝421＋42＝1617， f ⎝⎛⎭⎫14＝⎝⎛⎭⎫1421＋⎝⎛⎭⎫142＝117，所以f(1)＋f(2)＋f ⎝⎛⎭⎫12＋f(3)＋f ⎝⎛⎭⎫13＋f(4)＋f ⎝⎛⎭⎫14＝12＋45＋15＋910＋110＋1617＋117＝72. 解法二：由(1)知f(a)＋f ⎝⎛⎭⎫1a ＝1，所以f(2)＋f ⎝⎛⎭⎫12＝1，f(3)＋f ⎝⎛⎭⎫13＝1，f(4)＋f ⎝⎛⎭⎫14＝1，又f(1)＝121＋12＝12， 所以f(1)＋f(2)＋f ⎝⎛⎭⎫12＋f(3)＋f ⎝⎛⎭⎫13＋f(4)＋f ⎝⎛⎭⎫14＝12＋1＋1＋1＝72. 课时7 函数的定义域、值域1．函数的定义域是自变量的取值集合． 2．函数的值域是函数值的取值集合． 3．函数定义域的求法 (1)y ＝1f x中f(x)≠0. (2)y ＝f x 中f(x)≥0. (3)y ＝[f(x)]0中f(x)≠0.(4)当f(x)由几部分构成时，定义域是使各部分都有意义的实数的集合．(5)若f(x)是由实际问题列出的，则定义域是使解析式本身有意义且符合实际意义的实数的集合.已知函数解析式求定义域A ．{x|x≤1}B ．{x|x≥0}C ．{x|x≥1，或x≤0}D ．{x|0≤x≤1}答案 D解析 由⎩⎪⎨⎪⎧1－x≥0，x≥0，解得0≤x≤1，故选D.2．[2016·重庆一中高一检测]函数f(x)＝2x ＋3x ＋1的定义域是________． 答案 ⎩⎨⎧⎭⎬⎫x ⎪⎪x≥－32且x≠－1 解析 若使函数有意义，则2x ＋3≥0且x ＋1≠0. ∴x≥－32且x≠－1.∴定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪x≥－32且x≠－1. 抽象函数的定义域3.________答案 [0,1]解析 ∵f(x)的定义域为[－1,1]， ∴－1≤2x －1≤1，∴0≤x≤1. ∴函数f(2x －1)的定义域为[0,1].简单函数的值域x≠5}－1≤y≤2，y≠0}，则y ＝f(x)的图象可能是( )答案 B解析 由y ＝f(x)的定义域为{x|－3≤x≤8且x≠5}，排除A 、D ，再由函数的定义知，对任意一个x 值都有唯一确定的y 值与它对应，排除C ，故选B.5．已知函数f(x)＝x 2－2x(－1≤x≤2)． (1)画出f(x)的图象； (2)根据图象写出f(x)的值域． 解 (1)f(x)的图象如图所示．(2)观察f(x)的图象可知，f(x)图象上所有点的纵坐标的取值范围是[－1,3]，则f(x)的值域是[－1,3].求函数定义域时忽视细节致误6.易错分析 解本题时考虑到1＋1x≥0解出x 的取值范围，未考虑到x≠0导致定义域解错．正解 ⎩⎪⎨⎪⎧1＋1x ≥0x≠0解得x≤－1或x>0.所以函数的定义域为(－∞，－1]∪(0，＋∞)．一、选择题1．[2016·广东深圳中学月考]已知函数y ＝1－x2x 2－3x －2，则其定义域为( )A ．(－∞，1]B ．(－∞，2]C.⎝⎛⎭⎫－∞，－12∪⎝⎛⎭⎫－12，1 D.⎝⎛⎭⎫－∞，－12∪⎝⎛⎦⎤－12，1 答案 D解析 要使式子1－x 2x 2－3x －2有意义，则⎩⎪⎨⎪⎧1－x≥02x 2－3x －2≠0，即⎩⎪⎨⎪⎧x≤1x≠2且x≠－12，所以x≤1且x≠－12，即该函数的定义域为⎝⎛⎭⎫－∞，－12∪⎝⎛⎦⎤－12，1，故选D. 2．[2016·北京海淀期末]函数y ＝－x 2＋1，－1≤x<2的值域是( ) A ．(－3,0] B ．(－3,1] C ．[0,1] D ．[1,5)答案 B解析 由y ＝－x 2＋1，x ∈[－1,2)，可知当x ＝2时，y min ＝－4＋1＝－3；当x ＝0时，y max ＝1，∵x≠2，∴函数的值域为(－3,1]，故选B.3．若A ＝{x|y ＝x ＋1}，B ＝{y|y ＝x 2＋1}，则A∩B 等于( ) A ．{x|x≥1} B ．{x|x≥－1} C ．{x|－1≤x≤1} D ．{x|x≥0} 答案 A解析 由A ＝{x|y ＝x ＋1}＝{x|x≥－1}，B ＝{y|y ＝x 2＋1}＝{x|x≥1}，∴A∩B ＝{x|x≥1}． 4．[2016·成都高一月考]已知a 为实数，则下列函数中，定义域和值域都有可能是R 的是( )A ．f(x)＝x 2＋aB ．f(x)＝ax 2＋1C ．f(x)＝ax 2＋x ＋1D ．f(x)＝x 2＋ax ＋1答案 C解析 A 中函数的值域为[a ，＋∞)； B 中函数，a ＝0时，值域为{1}，a>0时，值域为[1，＋∞)，a<0时，值域为(－∞，1]； C 中函数，a ＝0时，值域为R. a<0时，值域为⎝⎛⎤－∞，4a －14a .a>0时，值域为⎣⎡⎭⎫4a －14a ，＋∞； D 中函数的值域为⎣⎡⎭⎫4－a24，＋∞.5．下列函数中，值域为(0，＋∞)的是( ) A ．y ＝x B ．y ＝1xC ．y ＝1xD ．y ＝x 2＋1答案 B解析 A 中x≥0，所以y≥0；B 中x>0，所以y>0；C 中x≠0，所以y≠0；D 中，x ∈R ，所以y≥1，故选B.二、填空题6．已知函数f(x)＝2x －3，x ∈{x ∈N|1≤x≤5}，则函数f(x)的值域为________． 答案 {－1,1,3,5,7}解析 x ∈{x ∈N|1≤x≤5}＝{1,2,3,4,5}，∴x ＝1时y ＝－1；x ＝2时y ＝1；x ＝3时，y ＝3；x ＝4时，y ＝5；x ＝5时，y ＝7，∴y ∈{－1,1,3,5,7}．7．已知f(2x －1)的定义域为[－1,1]，则函数f(x)的定义域为________． 答案 [－3,1]解析 ∵f(2x －1)的定义域为[－1,1]， ∴x ∈[－1,1]．令t ＝2x －1，∴－3≤t≤1. ∴f(x)的定义域为[－3,1]．8．若函数f(x)的定义域是[0,1]，则函数f(2x)＋f ⎝⎛⎭⎫x ＋23的定义域为________． 答案 ⎣⎡⎦⎤0，13解析 由⎩⎪⎨⎪⎧0≤2x≤1，0≤x ＋23≤1，得⎩⎨⎧0≤x≤12，－23≤x≤13.即x ∈⎣⎡⎦⎤0，13. 三、解答题9．求下列函数的定义域． (1)f(x)＝5－x|x|－3； (2)y ＝x －1＋1－x. 解 (1)要使函数有意义，则⎩⎪⎨⎪⎧ 5－x≥0，|x|－3≠0，即⎩⎪⎨⎪⎧x≤5，x≠±3，在数轴上标出， 如图，即x<－3，或－3<x<3，或3<x≤5.故函数f(x)的定义域为(－∞，－3)∪(－3,3)∪(3,5]． 当然也可以表示为{x|x<－3，或－3<x<3，或3<x≤5}．(2)要使函数有意义，则⎩⎪⎨⎪⎧ x －1≥0，1－x≥0，即⎩⎪⎨⎪⎧x≥1，x≤1.所以x ＝1，从而函数的定义域为{1}． 10．求下列函数的值域． (1)y ＝x ＋1； (2)y ＝1－x x ＋2； (3)y ＝2x －x －1.解 (1)(观察法)因为x ≥0，所以x ＋1≥1，所以y ＝x ＋1的值域为[1，＋∞)． (2)(分离常数法)y ＝1－x x ＋2＝－ x ＋2 ＋3x ＋2＝－1＋3x ＋2，故y ＝1－x x ＋2的值域为{y|y ∈R 且y≠－1}．(3)(换元法)设t ＝x －1(x －1≥0)， 则t≥0且x ＝t 2＋1，所以y ＝2(t 2＋1)－t ＝2⎝⎛⎭⎫t －142＋158，由t≥0，可得函数的值域为⎣⎡⎭⎫158，＋∞. ►1.2.2 函数的表示法课时8 函数的表示法函数的三种表示法(1)解析法——用数学表达式表示两个变量之间的对应关系； (2)图象法——用图象表示两个变量之间的对应关系； (3)列表法——列出表格来表示两个变量之间的对应关系.1.已知A ．0 B ．2f(x) C ．－2f(x) D ．2f(－x)答案 A解析 f(x)＋f(－x)＝x 3－x －x 3＋x ＝0.2．一个面积为100 cm 2的等腰梯形，上底长为x cm ，下底长为上底长的3倍，则把它的高y 表示成x 的函数为( )A ．y ＝50x(x ＞0)B ．y ＝100x(x ＞0)C ．y ＝50x (x ＞0)D ．y ＝100x(x ＞0) 答案 C解析 由x ＋3x 2·y ＝100，得2xy ＝100.∴y ＝50x(x ＞0).3.A ．96件B ．97件C ．107件D ．108件答案 C。

加油！有志者事竟成答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。

２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，有什么题型，哪些容易，哪些难，做到心里有底；３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应该多读几遍，比如从小到大，从左到右这样的题；４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏的小题；５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读题，结合平时课堂上所学的知识，解答难题；一定要镇定，不能因此慌了手脚，影响下面的答题；６、卷面要清洁，字迹要清工整，非常重要；７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。

亲爱的朋友，你们好!经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。

相信你是最棒的！第三章综合测试一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.某同学用二分法求方程338=0x x +-在()12x ∈，内近似解的过程中，设()=338x f x x +-，且计算()10f ＜，()20f ＞，()1.50f ＞，则该同学在第二次应计算的函数值为（ ）A .()0.5fB .()1.125fC .()1.25fD .()1.75f2.函数()22=log f x x x +的零点所在的区间为（ ）A .1142⎛⎫ ⎪⎝⎭，B .112⎛⎫ ⎪⎝⎭，C.(D.)23.有一组实验数据如表所示：x 1 2 3 4 5 y1.55.913.424.137下列所给函数模型较适合的是（ ） A .()=log 1a y x a ＞B .()=1y ax b a +＞C .()2=0y ax b a +＞D .()=log 1a y x b a +＞4.根据表中的数据，可以判定方程2=0x e x --的一个根所在的区间为（ ）x 1-0 1 2 3 x e0.37 1 2.72 7.39 20.09 2x +1 23 45A .()1-，B .()01，C .()12，D .()23，5.某家具的标价为132元，若降价以九折出售（即优惠10％），仍可获利10％（相对进货价），则该家具的进货价是（ ） A .108元B .105元C .106元D .118元6.有一个盛水的容器，由悬在它上空的一根水管匀速向容器内注水，直至把容器注满.在注水过程中，时刻t 与水面高度y 的函数关系如图所示，图中PQ 为一线段，则与之对应的容器的形状是图中的（ ）AB CD7.已知()()()=2f x x a x b ---，并且α，β是函数()f x 的两个零点，则实数a ，b ，α，β的大小关系可能是（ ）A .a b αβ＜＜＜B .a b αβ＜＜＜C .a b αβ＜＜＜D .a b αβ＜＜＜8.函数()2230=2ln 0x x x f x x x ⎧+-⎨-+⎩，≤，，＞的零点个数为（ ）A .0B .1C .2D .39.已知函数()231=24log f x x x x-+++，若()113x ∈，，()23x ∈+∞，，则（ ） A.()10f x ＞，()20f x ＜ B.()10f x ＜，()20f x ＞ C.()10f x ＜，()20f x ＜D.()10f x ＞，()20f x ＞10.如图所示，ABC △为等腰直角三角形，直线l 与AB 相交且l AB ⊥，直线l 截这个三角形所得的位于直线右方的图形面积为y ，点A 到直线l 的距离为x ，则()=y f x 的图像大致为四个选项中的（ ）AB CD11.设某公司原有员工100人从事产品A 的生产，平均每人每年创造产值t 万元（t 为正常数）.公司决定从原有员工中分流()0100x x ＜＜人去进行新开发的产品B 的生产.分流后，继续从事产品A 生产的员工平均每人每年创造产值在原有的基础上增长了1.2x ％.若要保证产品A 的年产值不减少，则最多能分流的人数是（ ）A .15 B .16 C .17 D .18 12.已知函数()2=e x xf x --（e 为自然对数的底数），则方程()21=0f x -的实数根的个数为（ ）A .1B .2C .3D .4二、填空题：本大题共4小题，每小题5分，共20分.13.用二分法求图像连续不断的函数()f x 在区间[]15，上的近似解，验证()()150f f ⋅＜，给定精确度=0.01ε，取区间()15，的中点115==32x +，计算得()()110f f x ⋅＜，()()150f x f ⋅＞，则此时零点0x ∈________.（填区间）14.已知函数()2=log 2x f x x m +-有唯一的零点，若它的零点在区间()12，内，则实数m 的取值范围是________.15.已知关于x 的方程210=x a -有两个不同的实根1x ，2x ，且21=2x x ，则实数=a ________.16.某市出租车收费标准如下：起步价为8元，起步里程为3km （不超过3km 按起步价付费）；超过3km 但不超过8km 时，超过部分按每千米2.15元收费；超过8km 时，超过部分按每千米2.85元收费.另每次乘坐需付燃油附加费1元.现某人乘坐一次出租车付费22.6元，则此次出租车行驶的路程为________km . 三、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.17.（本小题满分10分）某公司制定了一个激励销售人员的奖励方案：当销售利润不超过10万元时，按销售利润的16％进行奖励；当销售利润超过10万元时，若超出A 万元，则超出部分按()52log 1A +万元进行奖励.记奖金为y （单位：万元），销售利润为x （单位：万元）. （1）写出该公司激励销售人员的奖励方案的函数模型.（2）如果业务员老张获得5.6万元的奖金，那么他的销售利润是多少万元？18.（本小题满分12分）已知函数()=211f x x x --+. （1）请在所给的平面直角坐标系中画出函数()f x 的图像.（2）根据函数()f x 的图像回答下列问题：（回答下述3个小题都只需直接写出结果，不需给出演算步骤） ①求函数()f x 的单调区间；②求函数()f x 的值域；③求关于x 的方程()=2f x 在区间[]02，上解的个数.19.（本小题满分12分）已知函数()=e 1x f x -，()3=1exg x +.（1）求函数()g x 的值域；（2）求满足方程()()=0f x g x -的x 的值.20.（本小题满分12分）《污水综合排放标准》规定：污水排放企业进排污口的污水pH 值正常范围为[)69，.某化工企业对本单位污水出水口的pH 值进行全天24小时检测，根据统计资料发现pH 值的大小y 与检测时间点x 之间的函数图像如图所示，AB ，CD 为两条直线段，曲线BC 为函数y b +图像的一部分，其中()08A ，，()46B ，，()2010C ，，()248D ，.（1）请写出pH 值的大小y 与检测时间点x 之间的函数解析式；（2）试求该化工企业在一天内排放pH 值超标污水的时长.21.（本小题满分12分）已知函数()2=283f x x x m -++为R 上的连续函数.（1）若=4m -，试判断()=0f x 在()11-，上是否有根存在.若没有，请说明理由；若有，请在精确度为0.2（即根所在区间长度小于0.2）的条件下，用二分法求出使这个根0x 存在的区间.（2）若函数()f x 在区间[]11-，上存在零点，求实数m 的取值范围.22.（本小题满分12分）已知函数()()2=log 421x x f x a a +⋅++，x ∈R . （1）若=1a ，求方程()=3f x 的解集；（2）若方程()=f x x 有两个不同的实数根，求实数a 的取值范围.第三章综合测试答案解析一、 1.【答案】C【解析】()10f ＜，()20f ＞，()1.50f ＞，∴在区间()11.5，内函数()=338x f x x +-存在一个零点，因此在第二次应计算的函数值所对应的x 值为1 1.5=1.252+，故选C . 2.【答案】B【解析】 函数()22=log f x x x +在0x ＞时是连续单调递增函数，且()21=1log 1=10f +＞，21113=log =02424f ⎛⎫+- ⎪⎝⎭，()1102ff ⎛⎫∴⋅ ⎪⎝⎭＜.∴函数()22=log f x x x +的零点所的在区间是112⎛⎫ ⎪⎝⎭. 3.【答案】C【解析】由所给数据可知y 随x 的增大而增大，且增长速度越来越快，而A ，D 中的函数增长速度越来越慢，B 中的函数增长速度保持不变，故选C . 4.【答案】C【解析】设()()=2x f x e x -+，则由题设知()1=0.280f -＜，()2=3.390f ＞，故方程2=0x e x --的一个根在区间()12，内.故选C . 5.【答案】A【解析】由题意，132元打9折，售价为()1320.9=118.8⨯元.因为这个价格相对进货价，获利10％，也就是说它是进货价的110％，所以进货价为()110118.8=108÷％元，故选A . 6.【答案】B【解析】由题中函数图像知，水面高度y 上升的速度先是由慢到快，后来速度保持不变，结合容器形状知选B . 7.【答案】C【解析】α ，β是函数()f x 的两个零点，()()==0f f αβ∴.又()()==20f a f b - ＜，结合二次函数的图像（如图所示）可知a ，b 必在α，β之间.故选C .【解析】当0x ≤时，令223=0x x +-，得=3x -；当0x ＞时，令2ln =0x -+，得2=e x .所以函数有2个零点.故选C . 9.【答案】A【解析】()()23=15log f x x x --+- 在()1+∞，上单调递减，且()3=0f ，()10f x ∴＞，()20f x ＜，故选A .10.【答案】C【解析】设=AB a ，则22221111==2222y a x x a --+，其图像为抛物线的一段，开口向下，顶点在y 轴上方.故选C . 11.【答案】B【解析】由题意，分流前产品A 的年产值为100t 万元，分流x 人后，产品A 的年产值为()()1001 1.2x x t-+％万元.由题意，得()()01001001 1.2100x x x x t t ∈⎧⎪⎨-+⎪⎩N ＜＜，≥，，％解得5003x ＜≤，x ∈N ，所以x 的最大值为16.故选B .12.【答案】B 【解析】由函数()2=ex xf x --，可知方程()21=0f x -，即()1=2f x ，即21e =2x x --，整理可得2=ln 2x x ---，即2ln 2=0x x -+或2ln 2=0x x --.在方程2ln 2=0x x -+中，1=14ln 20∆-＜，方程无实数解；在方程2ln 2=0x x --中，2=14ln 20∆+＞，方程有2个不等的实数解.综上可得，方程()21=0f x -的实数根的个数为2.故选B . 二、13.【答案】()13，【解析】由()()150f f ⋅＜，()()110f f x ⋅＜及()()150f x f ⋅＞可知()1f 与()1f x 异号，()1f x 与()5f 同号，则()011x x ∈，即()013x ∈，.14.【答案】()25，【解析】由题意得()f x 在()0+∞，上单调递增，且()()120f f ⋅＜，即()()250m m --＜，解得25m ＜＜. 15.【答案】6【解析】由210=x a -得2=10x a ±，由题设知12=10x a -，22=10x a +.因为21=2x x ，所以()211222=2=2x x x ，所以()210=10a a -+，解得=15a 或=6a .因为100a -＞，所以=15a 不合题意，舍去，所以=6a .【解析】设乘客每次乘坐出租车需付费用为()f x 元，则由题意得()(]()(]()()8103=93 2.153895 2.158 2.858.x f x x x x x ⎧+∈⎪+-∈⎨⎪++-∈+∞⎩⨯⨯⨯，，，，，，，，令()=22.6f x ，显然()()95 2.158 2.85=22.68x x ⨯⨯++-＞，解得=9x . 三、17.【答案】（1）由题意得()50.16010= 1.62log 910.x x y x x ⎧⎪⎨+-⎪⎩，＜≤，，＞（2）由(]010x ∈，，0.16 1.6x ≤，而=5.6y 可知，10x ＞. ()51.62log 9=5.6x ∴+-，解得=34x .∴老张的销售利润是34万元.18.【答案】（1）当10x -≥，即1x ≥时，()()=211=1f x x x x --+-； 当10x -＜，即1x ＜时，()()=211=33f x x x x --+-.()f x 的图像如图所示.（2）①函数()f x 的单调递增区间为[)1+∞，；函数()f x 的单调递减区间为(]1-∞，. ②函数()f x 的值域为[)0+∞，.③方程()=2f x 在区间[]02，上解的个数为1. 19.【答案】（1）()31=1=31e e x x g x ⎛⎫++ ⎪⎝⎭，因为0x ≥，e 1x≥，所以101e x ⎛⎫ ⎪⎝⎭＜≤，1033e x⎛⎫ ⎪⎝⎭＜≤，即()14g x ＜≤，故()g x 的值域是(]14，. （2）由()()=0f x g x -，得3e 2=0ex x--.当0x ≤时，方程无解； 当0x ＞时，3e 2=0ex x--，整理得()2e 2e 3=0x x --， 即()()e 1e 3=0x x +-.因为e 0x ＞，所以e =3x ，即=ln3x . 故满足方程()()=0f x g x -的x 的值为ln3.20.【答案】（1）()08A ，，()46B ，， ∴线段AB 的方程是()1=8042y x x -+≤≤.将()46B ，，()2010C ，的坐标代入y b +，得b b ⎧⎪⎨+⎪⎩，，解得=4=6.a b -⎧⎨⎩，故()6420y x +≤≤.()2010C ，，()248D ，，∴线段CD 的方程是()1=2020242y x x -+≤≤.综上，y 与x之间的函数解析式为18042=642012020242.x x y x x x ⎧-+⎪+⎪-+⎪⎩，≤≤，，≤≤，，≤≤ （2）由()08A ，，()46B ，知在AB 段排放污水的pH 值不超标； 在BC6=9+，解得=13x ， 故[)1320x ∈，时排放污水的pH 值超标， 时长是()2013=7-小时；在CD 段，令120=92x -+，解得=22x ，故[]2022x ∈，时排放污水的pH 值超标，时长是()2220=2-小时.因此该化工企业在一天内排放pH 值超标污水9小时.21.【答案】（1）当=4m -时，()=0f x ，即()2=281=0f x x x --.可以求出()1=9f -，()1=7f -，则()()110f f -⋅＜.又()f x 为R 上的连续函数，()=0f x ∴在()11-，上必有根存在.取中点0，计算得()0=10f -＜，()()100f f -⋅＜，∴根()010x ∈-，，取其中点12-，计算得17=022f ⎛⎫- ⎪⎝⎭＞， ∴根0102x ⎛⎫∈- ⎪⎝⎭，，取其中点14-，计算得19=048f ⎛⎫- ⎪⎝⎭， ∴根0104x ⎛⎫∈- ⎪⎝⎭，，取其中点18-，计算得11=0832f ⎛⎫- ⎪⎝⎭＞， ∴根0108x ⎛⎫∈- ⎪⎝⎭，，区间长度11=0.285，符合要求. 故符合要求的根0x 存在的区间为108⎛⎫- ⎪⎝⎭，. （2）()2=283f x x x m -++为开口向上的抛物线，对称轴为8==222x ⨯--， ∴在区间[]11-，上，函数()f x 单调递减.又()f x 在区间[]11-，上存在零点，只可能()()1010f f ⎧-⎪⎨⎪⎩≥，≤，即 28302830m m +++⎧⎨-++⎩≥，≤，解得133m -≤≤. 故所求实数m 的取值范围是133m -≤≤.22.【答案】（1）当=1a 时，()()2=log 422x x f x ++.由()=3f x ，得3422=2x x ++，所以426=0x x +-，因此()()2322=0x x +-，解得=1x .所以方程()=3f x 的解集为{}1.（2）方程()2log 421=x x a a x +⋅++有两个不同的实数根，即421=2x x x a a +⋅++有两个不同的实数根.设=2x t ，则()211=0t a t a +-++在()0+∞，上有两个不同的解.令()()2=11g t t a t a +-++，由已知可得 ()()()200102=1410g a a a ⎧⎪-⎪-⎨⎪⎪∆--+⎩＞，＞，＞，解得13a --＜＜ 故实数a的取值范围为(13--，.。

必修一人教版第三章检测试卷(100分)一、选择题(本题包括18小题，每小题3分，共54分。

每小题只有一个选项符合题意)1．(2020·云南省新平一中月考)金属单质四兄弟W、X、Y、Z不小心掉到稀盐酸池中，反应如图所示，则它们的活动性由强到弱的顺序是( )A．X>W>Z>Y B．Z>X>W>YC．W>X>Y>Z D．Y>Z>X>W答案 B2．下列叙述不正确的是( )答案 D3．(2020·合肥市双墩中学第三次月考)一定条件下，下列物质可通过化合反应制得的共有( )①小苏打②硫酸铝③氯化亚铁④磁性氧化铁⑤氢氧化铁A．3种 B．4种 C．5种 D．2种答案 B4、已知如下三个实验均能发生化学反应：下列判断正确的是( )A．实验①中铁作还原剂B．实验②中Fe2＋既显氧化性又显还原性C．实验③中发生的是置换反应D．上述实验证明氧化性：Fe3＋>Fe2＋>Cu2＋答案 A5．下列关于几种金属的叙述正确的是( )A．金属钠与H2O、酸溶液反应时，钠都是还原剂B．金属铁与水蒸气反应可得到氧化铁C．钠与氧气反应时，产物是由参加反应的O2的量决定的D．镁粉中含有少量铝粉可加入盐酸除去答案 A6．碲锌镉(Te­Zn­Cd)晶体可以用于制造红外探测器，下列有关它的叙述中不正确的是( )A．它是由Te、Zn、Cd按一定比例混合而成的，无固定的熔、沸点B．它易导电、导热，具有延展性C．它的熔、沸点比Zn的低D．它的硬度和强度比Cd的大答案 A7．(2020·赣州市赣县三中月考)下列物质中既能与稀H2SO4反应，又能与NaOH溶液反应的是( )①NaHCO3②Al2O3③Al④Na2CO3⑤NaHSO4A．②③④ B．①②③ C．①③④ D．全部答案 B8．(2020·山西省应县一中月考)下列各组物质相互混合反应，既有气体生成最终又有沉淀生成的是( )①金属钠投入MgCl2溶液中②过量的NaOH溶液和FeCl3溶液③过量的Na2O2投入FeCl2溶液中④过量NaOH和Ca(HCO3)2溶液混合A．①④ B．②③ C．①③ D．③④答案 C9．(2020·内蒙古翁牛特旗乌丹一中期中)下列推理正确的是( )A．铝粉在氧气中燃烧生成Al2O3，故铁丝在氧气中燃烧生成Fe2O3B．铁能从硫酸铜溶液中置换出铜，故钠也能从硫酸铜溶液中置换出铜C．钠与O2、水等反应时钠均作还原剂，故金属单质参与化学反应时金属均作还原剂D．活泼金属钠保存在煤油中，故活泼金属铝也保存在煤油中答案 C10．验证Fe3＋与Fe2＋能够相互转化。

第一章单元质量测评(一)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，满分150分，考试时间120分钟．第Ⅰ卷(选择题，共60分)一、选择题(本大题共12小题，每小题5分，共60分)1．[2015·广东高考]已知集合M＝{－1,0,1}，N＝{0,1,2}，则M ∪N＝()A．{0,1} B．{－1,0,2}C．{－1,0,1,2} D．{－1,0,1}答案 C解析依题意得M∪N＝{－1,0,1,2}，故选C.2．[2015·天津高考]已知全集U＝{1,2,3,4,5,6,7,8}，集合A＝{2,3,5,6}，集合B＝{1,3,4,6,7}，则集合A∩∁U B＝()A．{2,5} B．{3,6}C．{2,5,6} D．{2,3,5,6,8}答案 A解析因为∁U B＝{2,5,8}，又A＝{2,3,5,6}，所以A∩∁U B＝{2,5}，故选A.3．50名同学参加跳远和铅球测验，跳远和铅球测验成绩分别为及格40人和31人，2项测验成绩均不及格的有4人，2项测验成绩都及格的人数是()A．35 B．25C．28 D．15答案 B解析全班分4类人：设两项测验成绩都及格的人数为x人；仅跳远及格的人数为(40－x)人；仅铅球及格的人数为(31－x)人；两项都不及格的人数为4人，∴40－x＋31－x＋x＋4＝50，∴x＝25.4．[2015·陕西工大附中高一质检]如图所示的韦恩图中A，B是非空集合，定义集合A *B 为阴影部分表示的集合，则A *B ＝( )A ．∁U (A ∪B ) B ．A ∪(∁U B )C ．(∁U A )∪(∁U B )D ．(A ∪B )∩∁U (A ∩B )答案 D解析 阴影部分为A ∪B 去掉A ∩B 后的部分，为(A ∪B )∩∁U (A ∩B )．选D.5．函数f (x )是定义在[0，＋∞)上的增函数，则满足f (2x －1)<f ⎝ ⎛⎭⎪⎫13的x 的取值范围是( )A.⎝ ⎛⎭⎪⎫13，23B.⎣⎢⎡⎭⎪⎫13，23 C.⎝ ⎛⎭⎪⎫12，23 D.⎣⎢⎡⎭⎪⎫12，23 答案 D 解析根据题意，得⎩⎨⎧2x －1≥0，2x －1<13，解得12≤x <23，选D.6．[2015·攀枝花米易中学月考]已知函数f (x )的定义域为(3－2a ，a ＋1)，且f (x ＋1)为偶函数，则实数a 的值可以是( )A ．2 B.23 C ．4 D ．6答案 A解析 因为函数f (x )的定义域为(3－2a ，a ＋1)，所以在函数f (x ＋1)中，3－2a ＜x ＋1＜a ＋1，则函数f (x ＋1)的定义域为(2－2a ，a )，又因为f (x ＋1)为偶函数，所以2－2a ＝－a ，a ＝2，故选A.7．[2015·衡水高一调研]已知函数y ＝f (x ＋1)定义域是[－2,3]，则y ＝f (x －1)的定义域是( )A ．[0,5]B ．[－1,4]C ．[－3,2]D ．[－2,3]答案 A解析 由题意知，－2≤x ≤3，∴－1≤x ＋1≤4.∴－1≤x －1≤4，得0≤x ≤5，即y ＝f (x －1)的定义域为[0,5]． 8．[2016·湖南浏阳一中期中]若函数f (x )(f (x )≠0)为奇函数，则必有( )A ．f (x )f (－x )>0B ．f (x )f (－x )<0C ．f (x )<f (－x )D ．f (x )>f (－x ) 答案 B解析 ∵f (x )为奇函数，∴f (－x )＝－f (x )，又f (x )≠0，∴f (x )f (－x )＝－[f (x )]2<0.9．函数f (x )的定义域为R ，若f (x ＋y )＝f (x )＋f (y )，f (8)＝3，则f (2)＝( )A.54B.34 C.12 D.14答案 B解析 依题意得f (x ＋y ＋z ＋w )＝f (x ＋y )＋f (z ＋w )＝f (x )＋f (y )＋f (z )＋f (w )，令x ＝y ＝z ＝w ＝2可得f (8)＝4f (2)，因此代入f (8)＝3可解得f (2)＝34，选B.10．下图所给4个图象中，与所给3件事吻合最好的顺序为( ) (1)小明离开家不久，发现自己把作业本忘在家里了，于是立刻返回家里取了作业本再上学；(2)小明骑着车一路以匀速行驶，只是在途中遇到一次交通堵塞，耽搁了一些时间；(3)小明出发后，心情轻松，缓缓行进，后来为了赶时间开始加速．A ．(1)(2)(4)B ．(4)(2)(3)C ．(4)(1)(3)D ．(4)(1)(2)答案 D解析 事件(1)中因为返回，故回家后距离应该为0，应该选图象(4)；事件(2)中交通堵塞，就是说离开家的距离停顿下来，故应该选图象(1)；事件(3)说明速度先慢后快，故选图象(2)．11．[2016·南安高一检测]已知函数f (x )＝ax 2－x ＋1在(－∞，2)上是单调递减的，则a 的取值范围是( )A.⎝ ⎛⎦⎥⎤0，14 B.⎣⎢⎡⎦⎥⎤0，14 C ．[2，＋∞) D ．(0,4] 答案 B解析 当a ＝0时，f (x )＝－x ＋1在(－∞，2)上是单调递减的；当a ≠0时，要使f (x )在(－∞，2)上单调递减．则⎩⎨⎧a >0，－－12a ≥2，所以0<a ≤14.综上可得a 的取值范围为a ∈⎣⎢⎡⎦⎥⎤0，14.12．已知函数f (x )＝4x 2－mx ＋5在区间[－2，＋∞)上是增函数，则f (1)的取值范围是( )A ．f (1)≥25B ．f (1)＝25C ．f (1)≤25D ．f (1)>25答案 A解析 ∵函数f (x )＝4x 2－mx ＋5的图象对称轴为x ＝m 8，则有m8≤－2，∴m ≤－16，而f (1)＝4－m ＋5＝9－m ，∴f (1)≥25.第Ⅱ卷 (非选择题，共90分)二、填空题(本大题共4小题，每小题5分，共20分) 13．函数y ＝x ＋1＋12－x 的定义域为________．答案 [－1,2)∪(2，＋∞)解析 由题意知⎩⎪⎨⎪⎧x ＋1≥0，2－x ≠0，∴x ≥－1且x ≠2.14．[2016·江苏盐城中学月考]设函数f (x )＝⎩⎪⎨⎪⎧x 2＋1，x ≤1x 2＋x －2，x ＞1，则f [f (－1)]的值为________．答案 4解析 ∵f (－1)＝(－1)2＋1＝2， ∴f [f (－1)]＝f (2)＝22＋2－2＝4.15．[2016·荆州市中学期中]已知A 是有限集合，x ∉A ，B ＝A ∪{x }，若A ，B 的子集个数分别为a ，b ，且b ＝ka ，则k ＝________.答案 2解析 不妨设集合A 中的元素个数为n ，则集合B 中的元素个数有n ＋1，所以a ＝2n ，b ＝2n ＋1，因此b ＝2a ，故所求k 的值为2.16．函数f (x )＝2x 2－3|x |的单调减区间是________． 答案 ⎝⎛⎭⎪⎫－∞，－34，⎝⎛⎭⎪⎫0，34解析 f (x )＝⎩⎪⎨⎪⎧2x 2－3x (x ≥0)2x 2＋3x (x <0)，图象如下图所示f (x )减区间为⎝⎛⎭⎪⎫－∞，－34，⎝ ⎛⎭⎪⎫0，34.三、解答题(本大题共6小题，满分70分)17．[2016·郑州高一检测](本小题满分10分)全集U ＝R ，若集合A ＝{x |3≤x <10}，B ＝{x |2<x ≤7}．(1)求A ∩B ，A ∪B ，(∁U A )∩(∁U B )；(2)若集合C ＝{x |x >a }，A ⊆C ，求a 的取值范围． 解 (1)A ∩B ＝{x |3≤x <10}∩{x |2<x ≤7}＝{x |3≤x ≤7}； A ∪B ＝{x |3≤x <10}∪{x |2<x ≤7}＝{x |2<x <10}； (∁U A )∩(∁U B )＝{x |x ≤2，或x ≥10}．(2)A ＝{x |3≤x <10}，C ＝{x |x >a }，要使A ⊆C ，结合数轴分析可知a <3，即a 的取值范围是{a |a <3}．18．[2016·云南玉溪一中高一期中](本小题满分12分)设集合A＝{a ，a 2，b ＋1}，B ＝{0，|a |，b }且A ＝B .(1)求a ，b 的值；(2)判断函数f (x )＝－bx －ax 在[1，＋∞)的单调性，并用定义加以证明．解 (1)由集合A ＝B 知，a ≠0，∴b ＋1＝0，即b ＝－1.此时A ＝{a ，a 2,0}，B ＝{0，|a |，－1}，∴a ＝－1，∴A ＝{－1,1,0}，B ＝{0,1，－1}．满足集合的互异性， ∴a ＝－1，b ＝－1.(2)由(1)知f (x )＝x ＋1x ，f (x )＝x ＋1x 在[1，＋∞)上单调递增． 任取x 1，x 2∈[1，＋∞)且x 1＜x 2，f (x 1)－f (x 2)＝⎝ ⎛⎭⎪⎫x 1＋1x 1－⎝ ⎛⎭⎪⎫x 2＋1x 2＝(x 1－x 2)＋x 2－x 1x 1·x 2＝(x 1－x 2)⎝⎛⎭⎪⎫1－1x 1·x 2＝(x 1－x 2)x 1·x 2－1x 1·x 2， ∵x 1，x 2∈[1，＋∞)且x 1＜x 2， ∴x 1－x 2＜0，x 1·x 2－1＞0，x 1·x 2＞0， 所以f (x 1)－f (x 2)＜0，即f (x 1)＜f (x 2)， 所以f (x )＝x ＋1x 在[1，＋∞)上单调递增．19．[2016·淄博高一检测](本小题满分12分)设函数f (x )是定义在R 上的奇函数，若当x ∈(0，＋∞)时，f (x )＝3x ·(1＋x )．(1)求f (27)与f (－27)的值； (2)求f (x )的解析式．解 (1)由题意知f (27)＝327×(1＋27)＝84，f (－27)＝－f (27)＝－84，所以f (27)＝84，f (－27)＝－84.(2)因为f (x )是定义在R 上的奇函数，所以f (0)＝0. 设x <0，则－x >0，则f (－x )＝3－x ·[1＋(－x )]＝－3x ·(1－x )． 又f (－x )＝－f (x )， 所以f (x )＝3x (1－x )， 所以f (x )＝⎩⎪⎨⎪⎧3x (1＋x )，x >0，0，x ＝0，3x (1－x )，x <0.20．(本小题满分12分)已知函数f (x )＝x 2＋2x ＋ax ，x ∈[1，＋∞)． (1)当a ＝12时，判断并证明f (x )的单调性； (2)当a ＝－1时，求函数f (x )的最小值．解 (1)当a ＝12时，f (x )＝x 2＋2x ＋a x ＝x ＋2＋12x ＝x ＋12x ＋2. 设x 1，x 2是[1，＋∞)上的任意两个实数，且x 1<x 2， 则f (x 1)－f (x 2)＝⎝ ⎛⎭⎪⎫x 1＋12x 1－⎝ ⎛⎭⎪⎫x 2＋12x 2＝(x 1－x 2)＋⎝ ⎛⎭⎪⎫12x 1－12x 2＝(x 1－x 2)＋x 2－x 12x 1x 2＝(x 1－x 2)⎝ ⎛⎭⎪⎫1－12x 1x 2＝(x 1－x 2)·x 1x 2－12x 1x 2. 因为1≤x 1＜x 2，所以x 1－x 2<0，x 1·x 2>1， x 1x 2－12>0，所以f (x 1)－f (x 2)<0，即f (x 1)<f (x 2)． 所以函数f (x )在[1，＋∞)上是增函数． (2)当a ＝－1时，f (x )＝x －1x ＋2.因为函数y 1＝x 和y 2＝－1x 在[1，＋∞)上都是增函数，所以f (x )＝x －1x ＋2在[1，＋∞)上是增函数．当x ＝1时，f (x )取得最小值f (1)＝1－11＋2＝2， 即函数f (x )的最小值为2.21．(本小题满分12分)定义在实数集R 上的函数y ＝f (x )是偶函数，当x ≥0时，f (x )＝－4x 2＋8x －3.(1)求f (x )在R 上的表达式；(2)求y ＝f (x )的最大值，并写出f (x )在R 上的单调区间(不必证明)． 解 (1)设x <0，则－x >0.f (－x )＝－4(－x )2＋8(－x )－3＝－4x 2－8x －3. ∵f (x )是R 上的偶函数，∴f (－x )＝f (x )． ∴当x <0时，f (x )＝－4x 2－8x －3.∴f (x )＝⎩⎪⎨⎪⎧－4x 2＋8x －3 (x ≥0)，－4x 2－8x －3 (x <0)， 即f (x )＝⎩⎪⎨⎪⎧－4(x －1)2＋1 (x ≥0)－4(x ＋1)2＋1 (x <0). (2)∵y ＝f (x )开口向下，∴y ＝f (x )有最大值，f (x )max ＝f (－1)＝f (1)＝1. 函数y ＝f (x )的单调递增区间是(－∞，－1]和[0,1]， 单调递减区间是[－1,0]和[1，＋∞)．22．[2015·许昌高一五校联考](本小题满分12分)已知函数f (x )的定义域为R ，对于任意的x ，y ∈R ，都有f (x ＋y )＝f (x )＋f (y )，且当x >0时，f (x )<0，若f (－1)＝2.(1)求证：f (x )为奇函数； (2)求证：f (x )是R 上的减函数； (3)求函数f (x )在区间[－2,4]上的值域．解 (1)证明：∵f (x )的定义域为R ，令x ＝y ＝0， 则f (0＋0)＝f (0)＋f (0)＝2f (0)，∴f (0)＝0. 令y ＝－x ，则f (x －x )＝f (x )＋f (－x )，即f(0)＝f(x)＋f(－x)＝0.∴f(－x)＝－f(x)，故f(x)为奇函数．(2)证明：任取x1，x2∈R，且x1<x2，则f(x2)－f(x1)＝f(x2)＋f(－x1)＝f(x2－x1)．又∵x2－x1>0，∴f(x2－x1)<0，∴f(x2)－f(x1)<0，即f(x1)>f(x2)．故f(x)是R上的减函数．(3)∵f(－1)＝2，∴f(－2)＝f(－1)＋f(－1)＝4.又f(x)为奇函数，∴f(2)＝－f(－2)＝－4，∴f(4)＝f(2)＋f(2)＝－8.由(2)知f(x)是R上的减函数，所以当x＝－2时，f(x)取得最大值，最大值为f(－2)＝4；当x＝4时，f(x)取得最小值，最小值为f(4)＝－8.所以函数f(x)在区间[－2,4]上的值域为[－8,4]．。

必修一第三章训练卷函数的应用（一）注意事项：1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．函数()1ln ,034,0x x f x x x -+>⎧=⎨+<⎩的零点个数为（ ）A ．3B ．2C ．1D ．02．下列给出的四个函数()f x 的图象中能使函数()1y f x =-没有零点的是（ ）3．若函数y ＝f (x )在区间(－2，2)上的图象是连续不断的曲线，且方程f (x )＝0在()2,2-上仅有一个实数根，则()()11f f -⋅的值（ ）A ．大于0B ．小于0C ．无法判断D ．等于零4．方程1lg x x -=必有一个根的区间是（ ） A ．()0.1,0.2B ．()0.2,0.3C ．()0.3,0.4D ．()0.4,0.5 5．方程2x －1＋x ＝5的解所在的区间是（ ） A ．(0，1)B ．(1，2)C ．(2，3)D ．(3，4)6．如下图1所示，阴影部分的面积S 是h 的函数(0≤h ≤H )，则该函数的图象是下面四个图形中的（ ）图17．某人2011年7月1日到银行存入a 元，若按年利率x 复利计算，则到2014年7月1日可取款（ ） A ．a (1＋x )2元B ．a (1＋x )4元 C ．a ＋(1＋x )3元D ．a (1＋x )3元8．已知函数()24f x mx =+，若在[]2,1-上存在x 0，使()00f x =，则实数m 的取值范围是（ ）A ．5,42⎡⎤⎢⎥⎣⎦B ．(][),21,-∞-+∞C ．[]1,2-D ．[]2,1-9．某商场宣传在节假日对顾客购物实行一定的优惠，商场规定：（1）如一次购物不超过200元，不予以折扣；（2）如一次购物超过200元但不超过500元，按标价予以九折优惠；（3）如一次购物超过500元，其中500元给予九折优惠，超过500元的部分给予八五折优惠．某人两次去购物，分别付款176元和432元，如果他只去一次购买同样的商品，则应付款（ ） A ．608元B ．574.1元C ．582.6元D ．456.8元10．若函数f(x)的零点与g(x)＝4x＋2x－2的零点之差的绝对值不超过0．25，则f(x)可以是（）A．f(x)＝4x－1B．f(x)＝(x－1)2C．f(x)＝e x－1D．()1ln2f x x⎛⎫=-⎪⎝⎭11．如图2，直角梯形OABC中，AB∥OC，AB＝1，OC＝BC＝2，直线l：x＝t截此梯形所得位于l左方图形的面积为S，则函数S＝f(t)的图象大致为（）图212．函数f(x)＝|x2－6x＋8|－k只有两个零点，则（）A．0k=B．1k>C．01k≤<D．1k>，或0k=二、填空题（本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上）13．用二分法求方程x3－2x－5＝0在区间(2，4)上的实数根时，取中点x1＝3，则下一个有根区间是__________．14．方程e x－x＝2在实数范围内的解有________个．15．某化工厂生产一种溶液，按市场要求杂质含量不超过0.1%，若初始时含杂质2%，每过滤一次可使杂质含量减少13，至少应过滤________次才能达到市场要求？(已知lg2＝0．3010，lg3＝0．4771)16．某公司欲投资13亿元进行项目开发，现有以下六个项目可供选择：项目 A B C D E F投资额(亿元)52646 1利润(千万元)0．550．40．60．50．90．1写项目代号)．三、解答题(本大题共6个大题，共70分，解答应写出文字说明，证明过程或演算步骤)17．(10分)已知函数f(x)＝2(m＋1)x2＋4mx＋2m－1，（1）m为何值时，函数的图象与x轴有两个交点？（2）如果函数的一个零点在原点，求m的值．18．(12分)设函数f(x)＝ax2＋(b－8)x－a－ab的两个零点分别是－3和2．（1）求f(x)；（2）当函数f(x)的定义域是[0，1]时，求函数f(x)的值域．19．(12分)设函数f(x)＝e x－m－x，其中m R，当m>1时，判断函数f(x)在区间(0，m)内是否存在零点．20．(12分)某公司试销一种成本单价为500元/件的新产品，规定试销时销售单价不低于成本单价，又不高于800元/件，经试销调查，发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y＝kx＋b的关系(如图所示)．（1）根据图象，求一次函数y＝kx＋b的表达式；（2）设公司获得的毛利润(毛利润＝销售总价－成本总价)为S元．试用销售单价x 表示利润S；并求销售单价定为多少时，该公司可获得最大毛利润？最大毛利润是多少？此时的销售量是多少？图4①163普通：上网资费2元/小时；②163A：每月50元(可上网50小时)，超过50小时的部分资费2元/小时；③ADSLD：每月70元，时长不限(其他因素均忽略不计)．请你用所学的函数知识对上网方式与费用问题作出研究：（1）分别写出三种上网方式中所用资费与时间的函数解析式；（2）在同一坐标系内分别画出三种方式所需资费与时间的函数图象；（3）根据你的研究，请给刘老师一个合理化的建议．22．(12分)某企业常年生产一种出口产品，根据需求预测：进入21世纪以来，前8年在正常情况下，该产品产量将平衡增长．已知2000年为第一年，头4年年产量f(x)(万件)如表所示：（1）画出（2）建立一个能基本反映(误差小于0．1)这一时期该企业年产量发展变化的函数模型，并求之．（3）2006年(即x＝7)因受到某外国对我国该产品反倾销的影响，年产量应减少30%，试根据所建立的函数模型，确定2006年的年产量应该约为多少？2018-2019学年必修一第三章训练卷函数的应用（一）答 案一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的) 1．【答案】B【解析】当0x >时，令1ln 0x -+=，故e x =，符合；当0x <时，令340x +=，，符合，所以()y f x =的零点有2个，故选B ．2．【答案】C【解析】把()y f x =的图象向下平移1个单位后，只有C 图中图象与x 轴无交点． 故选C ． 3．【答案】C【解析】由题意不能断定零点在区间(－1，1)内部还是外部．故选C ． 4．【答案】A【解析】设()lg 1f x x x -+=，则()0.10.10.110.10f lg =-+=-<， f (0．2)＝lg0．2－0．2＋1≈0．1>0，f (0．1)f (0．2)<0，故选A ． 5．【答案】C 【解析】令f (x )＝2x －1＋x －5，则f (2)＝2＋2－5＝－1<0，f (3)＝22＋3－5＝2>0，从而方程在区间(2，3)内有解．故选C ． 6．【答案】C 【解析】当2Hh =时，对应阴影部分的面积小于整个图形面积的一半，且随着h 的增大，S 随之减小，故排除A 、B 、D ，选择C ． 7．【答案】D【解析】由题意知，2012年7月1日可取款a (1＋x )元， 2013年7月1日可取款a (1＋x )·(1＋x )＝a (1＋x )2元，2014年7月1日可取款a (1＋x )2·(1＋x )＝a (1＋x )3元．故选D ． 8．【答案】B【解析】由题意，知m ≠0，故f (x )是单调函数．又在[]2,1-上存在x 0，使f (x 0)＝0，所以f (－2)·f (1)≤0． 所以(－4m ＋4)·(2m ＋4)≤0，即(m －1)(m ＋2)≥0，得1020m m -≥⎧⎨+≥⎩或1020m m -≤⎧⎨+≤⎩，可解得m ≤－2，或m ≥1．故选B ．9．【答案】C【解析】本题实际上是一个分段函数的问题，购物付款432元，实际商品价值为104324809⨯=(元)；则一次购买标价为176＋480＝656(元)的商品应付款5000.91560.85582.6⨯+⨯＝ (元)，故选C ．10．【答案】A【解析】f (x )＝4x －1的零点为14x =，f (x )＝(x －1)2的零点为x ＝1， f (x )＝e x －1的零点为x ＝0，()1ln 2f x x ⎛⎫=- ⎪⎝⎭的零点为32x =，估算g (x )＝4x ＋2x －2的零点，因为g (0)＝－1，112g ⎛⎫= ⎪⎝⎭，所以g (x )的零点10,2x ⎛⎫∈ ⎪⎝⎭．又函数f (x )的零点与g (x )＝4x ＋2x －2的零点之差的绝对值不超过0．25， 只有f (x )＝4x －1的零点适合．故选A ． 11．【答案】C【解析】由题图可得函数的解析式为()2,0121,12t t S f t t t ⎧≤≤⎪==⎨-<≤⎪⎩．故选C ．12．【答案】D【解析】令y 1＝|x 2－6x ＋8|，y 2＝k ，由题意即要求两函数图象有两交点，利用数形结合思想，作出两函数图象可得选D ．二、填空题（本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上）13．【答案】(2，3)【解析】设f (x )＝x 3－2x －5，则f (2)<0，f (3)>0，f (4)>0，有f (2)f (3)<0，则下一个有根区间是(2，3)． 14．【答案】2【解析】可转化为判断函数y ＝e x 与函数y ＝x ＋2的图象的交点个数．图315．【答案】8【解析】设过滤n 次才能达到市场要求，则12%10.1%3n⎛⎫-≤ ⎪⎝⎭，即20.132n⎛⎫≤ ⎪⎝⎭，∴2lg 1lg23n ≤--．∴n ≥7．39，∴n ＝8．16．【答案】ABE (或BDEF )【解析】本题适用于估算来解决．首先确定出各个项目的利润与投资比：A ：0．11；B ：0．2；C ：0．1；D ：0．125；E ：0．15；F ：0．1，大小顺序是：B ，E ，D ，A ，C ，F ；而B ，E ，D 三项的利润和超过1．6千万元；但投资不到13亿元，只有12亿元，所以可以再加上F ，即B ，D ，E ，F ；或者去掉D 选A ，即A ，B ，E 也符合题意．三、解答题(本大题共6个大题，共70分，解答应写出文字说明，证明过程或演算步骤)17．【答案】（1）当m <1，且m ≠－1时，函数的图象与x 轴有两个交点；（2）12m =．【解析】（1）∵函数的图象与x 轴有两个交点，∴100m ∆+≠⎧⎨>⎩，即()()()214421210m m m m ≠-⎧⎪⎨-⨯+⋅->⎪⎩，整理得11m m ≠-⎧⎨<⎩． 即当m <1，且m ≠－1时，函数的图象与x 轴有两个交点． （2）∵函数的一个零点在原点，即点(0，0)在函数f (x )的图象上， ∴f (0)＝0，即2(m ＋1)·02＋4m ·0＋2m －1＝0．∴12m =． 18．【答案】（1）f (x )＝－3x 2－3x ＋18；（2）[]12,18．【解析】（1）∵f (x )的两个零点是－3和2， ∴函数图象过点(－3，0)、(2，0)． ∴9a －3(b －8)－a －ab ＝0，① 4a ＋2(b －8)－a －ab ＝0．② ①－②，得b ＝a ＋8．③③代入②，得4a ＋2a －a －a (a ＋8)＝0，即a 2＋3a ＝0．∵a ≠0，a ＝－3，∴b ＝a ＋8＝5．∴f (x )＝－3x 2－3x ＋18． （2）由（1）得()22133********f x x x x ⎛⎫=--+=-+++ ⎪⎝⎭，图象的对称轴方程是12x =-，且0≤x ≤1，∴f (x )min ＝f (1)＝12，f (x )max ＝f (0)＝18． ∴函数f (x )的值域是[]12,18． 19．【答案】存在零点．【解析】f (x )＝e x －m －x ，所以f (0)＝e －m －0＝e －m >0，f (m )＝e 0－m ＝1－m ． 又m >1，所以f (m )<0，所以f (0)·f (m )<0．又函数f (x )的图象在区间[0，m ]上是一条连续曲线， 故函数f (x )＝e x－m －x (m >1)在区间(0，m )内存在零点．20．【答案】（1）y ＝－x ＋1 000(500≤x ≤800)；（2）见解析． 【解析】（1）由图象知，当x ＝600时，y ＝400； 当x ＝700时，y ＝300．代入y ＝kx ＋b 中，得400600300700k b k b =+⎧⎨=+⎩，解得11000k b =-⎧⎨=⎩，∴y ＝－x ＋1 000(500≤x ≤800)（2）销售总价＝销量单价×销售量＝xy ，成本总价＝成本单价×销售量＝500y ， 代入求毛利润的公式，得S ＝xy －500y ＝x (－x ＋1 000)－500(－x ＋1 000)＝－x 2＋1 500x －500 000 ＝－(x －750)2＋62 500(500≤x ≤800)∴当销售单价为750元/件时，可获得最大毛利润62 500元，此时销售量为250件． 21．【答案】（1）见解析；（2）见解析；（3）见解析．【解析】（1）上网费用y(元)与上网时间t(小时)的函数关系：①163普通：y＝2t(t≥0)；②163A：()50,05050250,50tyt t≤≤⎧⎪=⎨+->⎪⎩，③ADSLD：y＝70(t≥0)；（2）如图5所示：图5（3）163普通：适合不常上网，偶尔上网的，当每月上网时间t≤25小时时，这种方式划算．163A：适合每月上网25～60小时的情况．ADSLD：每月上网时间t≥60小时的情况，用此方式比较合算．22．【答案】（1）见解析；（2）()3522f x x=+；（3）9.1万件．【解析】（1）散点图如图6：图6（2）设f(x)＝ax＋b．由已知得437a ba b+=⎧⎨+=⎩，解得32a=，52b=，∴()3522f x x=+．检验：f(2)＝5．5，|5．58－5．5|＝0．08<0．1；f(4)＝8．5，|8．44－8．5|＝0．06<0．1．∴模型()3522f x x=+能基本反映产量变化．（3）()35771322f=⨯+=，由题意知，2006年的年产量约为1370%9.1⨯=(万件)，即2006年的年产量应约为9.1万件．。