运筹学习题答案(第四章)

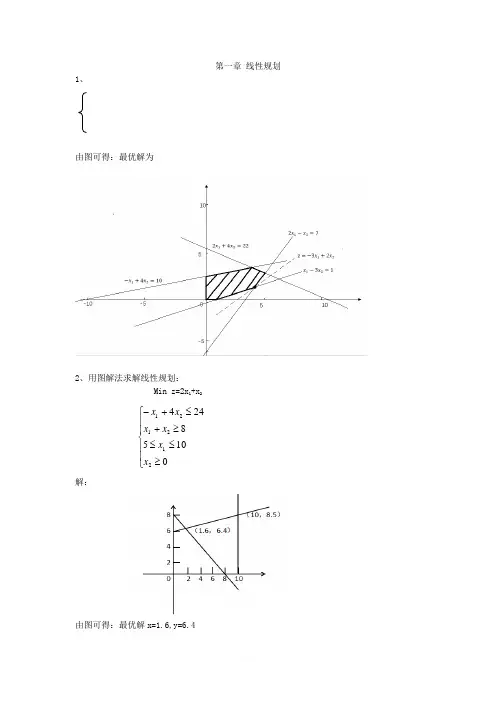
第一章 线性规划1、由图可得：最优解为2、用图解法求解线性规划： Min z=2x 1+x 2⎪⎪⎩⎪⎪⎨⎧≥≤≤≥+≤+-01058244212121x x x x x x解：由图可得：最优解x=1.6,y=6.4Max z=5x 1+6x 2⎪⎩⎪⎨⎧≥≤+-≥-0,23222212121x x x x x x解：由图可得：最优解Max z=5x 1+6x 2, Max z= +∞Maxz = 2x 1 +x 2⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤0,5242261552121211x x x x x x x由图可得：最大值⎪⎩⎪⎨⎧==+35121x x x ， 所以⎪⎩⎪⎨⎧==2321x xmax Z = 8.1212125.max 23284164120,1,2maxZ .jZ x x x x x x x j =+⎧+≤⎪≤⎪⎨≤⎪⎪≥=⎩如图所示，在（4，2）这一点达到最大值为26将线性规划模型化成标准形式：Min z=x 1-2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≥-=++-≥+-≤++无约束321321321321,0,052327x x x x x x x x x x x x解：令Z ’=-Z,引进松弛变量x 4≥0，引入剩余变量x 5≥0，并令x 3=x 3’-x 3’’,其中x 3’≥0,x 3’’≥0Max z ’=-x 1+2x 2-3x 3’+3x 3’’⎪⎪⎩⎪⎪⎨⎧≥≥≥≥≥≥-=++-=--+-=+-++0,0,0'',0',0,05232'''7'''5433213215332143321x x x x x x x x x x x x x x x x x x x7将线性规划模型化为标准形式Min Z =x 1+2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≤-=--≥++-≤++无约束，321321321321,00632442392-x x x x x x x x x x x x解：令Z ’ = -z ，引进松弛变量x 4≥0,引进剩余变量x 5≥0,得到一下等价的标准形式。

运筹学部分课后习题解答P47 1.1 用图解法求解线性规划问题a）12121212min z=23466 ..424,0x xx xs t x xx x++≥⎧⎪+≥⎨⎪≥⎩解：由图1可知，该问题的可行域为凸集MABCN，且可知线段BA上的点都为最优解，即该问题有无穷多最优解，这时的最优值为min 3z=23032⨯+⨯=P47 1.3 用图解法和单纯形法求解线性规划问题a）12121212max z=10x5x349 ..528,0x xs t x xx x++≤⎧⎪+≤⎨⎪≥⎩解：由图1可知，该问题的可行域为凸集OABCO，且可知B点为最优值点，即112122134935282xx xx x x=⎧+=⎧⎪⇒⎨⎨+==⎩⎪⎩，即最优解为*31,2Tx⎛⎫= ⎪⎝⎭这时的最优值为max335z=101522⨯+⨯=单纯形法： 原问题化成标准型为121231241234max z=10x 5x 349..528,,,0x x x s t x x x x x x x +++=⎧⎪++=⎨⎪≥⎩ j c →105B CB Xb 1x2x3x4x0 3x 9 3 4 1 0 04x8[5] 2 0 1 j j C Z -105 0 0 0 3x 21/5 0 [14/5] 1 -3/5 101x8/51 2/5 0 1/5 j j C Z -1 0 -2 5 2x 3/2 0 1 5/14 -3/14 101x11 0 -1/72/7j j C Z --5/14 -25/14所以有*max 33351,,1015222Tx z ⎛⎫==⨯+⨯= ⎪⎝⎭P78 2.4 已知线性规划问题：1234124122341231234max24382669,,,0z x x x x x x x x x x x x x x x x x x x =+++++≤⎧⎪+≤⎪⎪++≤⎨⎪++≤⎪≥⎪⎩求: (1) 写出其对偶问题；（2）已知原问题最优解为)0,4,2,2(*=X ，试根据对偶理论，直接求出对偶问题的最优解。

运筹学第三版课后习题答案第一章：引论1.1 课后习题习题1a)运筹学是一门应用数学的学科，旨在解决实际问题中的决策和优化问题。

它包括数学模型的建立、问题求解方法的设计等方面。

b)运筹学可以应用于各个领域，如物流管理、生产计划、流程优化等。

它可以帮助组织提高效率、降低成本、优化资源分配等。

c)运筹学主要包括线性规划、整数规划、指派问题等方法。

习题2运筹学的应用可以帮助组织提高效率、降低成本、优化资源分配等。

它可以帮助制定最佳的生产计划，优化供应链管理，提高运输效率等。

运筹学方法的应用还可以帮助解决紧急情况下的应急调度问题，优化医疗资源分配等。

1.2 课后习题习题1运筹学方法可以应用于各个领域，如物流管理、生产计划、供应链管理、流程优化等。

在物流管理中，可以使用运筹学方法优化仓储和运输的布局，提高货物的运输效率。

在生产计划中，可以使用运筹学方法优化产品的生产数量和生产周期，降低生产成本。

在供应链管理中，可以使用运筹学方法优化订单配送和库存管理，提高供应链的效率。

在流程优化中，可以使用运筹学方法优化业务流程，提高整体效率。

习题2在物流管理中，可以使用运筹学方法优化车辆的调度和路线规划，以提高运输效率和降低成本。

在生产计划中，可以使用运筹学方法优化生产线的安排和产品的生产量，以降低生产成本和提高产能利用率。

在供应链管理中，可以使用运筹学方法优化供应链各个环节的协调和调度，以提高整体效率和减少库存成本。

在流程优化中，可以使用运筹学方法优化业务流程的排布和资源的分配，以提高流程效率和客户满意度。

第二章：线性规划基础2.1 课后习题习题1线性规划是一种数学优化方法，用于解决包含线性约束和线性目标函数的优化问题。

其一般形式为：max c^T*xs.t. Ax <= bx >= 0其中，c是目标函数的系数向量，x是决策变量向量，A是约束矩阵，b是约束向量。

习题2使用线性规划方法可以解决许多实际问题，如生产计划、供应链管理、资源分配等。

第一章习题1.思考题（1）微分学求极值的方法为什么不适用于线性规划的求解（2）线性规划的标准形有哪些限制如何把一般的线性规划化为标准形式（3）图解法主要步骤是什么从中可以看出线性规划最优解有那些特点（4）什么是线性规划的可行解，基本解，基可行解引入基本解和基可行解有什么作用（5）对于任意基可行解，为什么必须把目标函数用非基变量表示出来什么是检验数它有什么作用如何计算检验数（6）确定换出变量的法则是什么违背这一法则，会发生什么问题{（7）如何进行换基迭代运算（8）大M法与两阶段法的要点是什么两者有什么共同点有什么区别（9）松弛变量与人工变量有什么区别试从定义和处理方式两方面分析。

（10）如何判定线性规划有唯一最优解，无穷多最优解和无最优解为什么2.建立下列问题的线性规划模型：（1）某厂生产A，B，C三种产品，每件产品消耗的原料和设备台时如表1-18所示：表1-18另外，要求三种产品总产量不低于65件，A的产量不高于B的产量。

试制定使总利润最大的模型。

（2）某公司打算利用具有下列成分（见表1-19）的合金配制一种新型合金100公斤，新合金含铅，锌，锡的比例为3：2：5。

,如何安排配方，使成本最低（3）某医院每天各时间段至少需要配备护理人员数量见表1-20。

表1-20初等数学的视察法，求出它的最优解（4）某工地需要30套三角架，其结构尺寸如图1-6所示。

仓库现有长6.5米的钢材。

如何下料，使消耗的钢材最少#;图1-63. 用图解法求下列线性规划的最优解：⎪⎪⎩⎪⎪⎨⎧≥≤+-≥+≥++=0,425.134 12 64 min )1(2121212121x x x x x x x x x x z⎪⎪⎩⎪⎪⎨⎧≥≤+≥+-≤++=0,82 5 1032 44 max )2(2121212121x x x x x x x x x x z⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤≤-≤+-≤++=0,6054 4 22232 96 max )3(21221212121x x x x x xx x x x x z⎪⎩⎪⎨⎧≥≤+-≥++=0,11234 3 max )4(21212121x x x x x x x x z{4. 把下列线性规划化为标准形式：⎪⎪⎩⎪⎪⎨⎧≥≤=-++-≥-+≤-+-+-=无约束432143213214313210,,01 32 212 min )1(x x x x x x x x x x x x x x x x x z⎪⎪⎩⎪⎪⎨⎧≤≤≥+-≤++=无约束211212121,02182 32 max )2(x x x x x x x x x z5. 判定下列集合是否凸集： （1）R 1=｛(x 1,x 2)|x 12+2x 22≤2｝（2）R 2=｛(x 1,x 2)|x 12－2x 2+3≥0,x 2≥0,|x 1|≤1｝ （3）R 3=｛(x 1,x 2)|x 1x 2≥1,x 1≥1,x 2≥0｝6. 求出下列线性规划的所有基本解，并指出其中的基可行解和最优解。

《运筹学》第四章习题一、思考题1．运输问题的数学模型具有什么特征？为什么其约束方程的系数矩阵的秩最多等于1-+n m ？2． 用左上角法确定运输问题的初始基本可行解的基本步骤是什么？3． 最小元素法的基本思想是什么？为什么在一般情况下不可能用它直接得到 运输问题的最优方案？4． 沃格尔法（V ogel 法）的基本思想是什么？它和最小元素法相比给出的运输问题的初始基本可行解哪一个更接近于最优解？为什么？5． 试述用闭回路法检验给定的调运方案是否最优的原理，其检验数的经济意义是什么？6． 用闭回路法检验给定的调运方案时，如何从任意空格出发去寻找一条闭回路？这闭回路是否是唯一的？7． 试述用位势法求检验数的原理、步骤和方法。

8． 试给出运输问题的对偶问题（对产销平衡问题）。

9． 如何把一个产销不平衡的运输问题（产大于销或销大于产）转化为产销平衡的运输问题。

10．一般线性规划问题应具备什么特征才可以转化为运输问题的数学模型？ 11．试述在表上作业法中出现退化解的涵义及处理退化解的方法。

二、判断下列说法是否正确1．运输问题模型是一种特殊的线性规划模型，所以运输问题也可以用单纯形方法求解。

2．因为运输问题是一种特殊的线性规划模型，因而求其解也可能出现下列四种情况：有唯一最优解；有无穷多个最优解；无界解；无可行解。

3．在运输问题中，只要给出一组（1-+n m ）个非零的{}j i x ，且满足∑==nj i j i a x 1，∑==mi j j i b x 1，就可以作为一个基本可行解。

4．表上作业法实质上就是求解运输问题的单纯形法。

5．按最小元素法或元素差额法给出的初始基本可行解，从每一空格出发都可以找到一闭回路，且此闭回路是唯一的。

6．如果运输问题单位运价表的某一行（或某一列）元素分别加上一个常数k ，最优调运方案将不会发生变化。

7．如果运输问题单位运价表的某一行（或某一列）元素分别乘上一个常数k ，最优调运方案将不会发生变化。

《管理运筹学》第四版课后习题解析第4章线性规划在工商管理中的应用1．解：为了用最少的原材料得到10台锅炉，需要混合使用14种下料方案。

设14种方案下料时得到的原材料根数分别为x1，x2，x3，x4，x5，x6，x7，x8，x9，x10，x11，x12，x13，x14，如表4-1所示。

表4-1 各种下料方式1234567891011121314s.t. 2x1＋x2＋x3＋x4≥80x2＋3x5＋2x6＋2x7＋x8＋x9＋x10≥350x3＋x6＋2x8＋x9＋3x11＋2x12＋x13≥420x4＋x7＋x9＋2x10＋x12＋2x13＋3x14≥10x1，x2，x3，x4，x5，x6，x7，x8，x9，x10，x11，x12，x13，x14≥0通过管理运筹学软件，我们可以求得此问题的解为：x1=40，x2=0，x3=0，x4=0，x5=116.667，x6=0，x7=0，x8=0，x9=0，x10=0，x11=140，x12=0，x13=0，x14=3.333最优值为300。

2．解：（1）将上午11时至下午10时分成11个班次，设x i表示第i班次新上岗的临时工人数，建立如下模型。

min f=16(x1＋x 2＋x3＋x4＋x5＋x6＋x7＋x8＋x9＋x10＋x11)s.t．x1＋1≥9x1＋x2＋1≥9x1＋x2＋x3＋2≥9x1＋x2＋x3＋x4＋2≥3x2＋x3＋x4＋x5＋1≥3x3＋x4＋x5＋x6＋2≥3x4＋x5＋x6＋x7＋1≥6x5＋x6＋x7＋x8＋2≥12x6＋x7＋x8＋x9＋2≥12x7＋x8＋x9＋x10＋1≥7x8＋x9＋x10＋x11＋1≥7x1，x2，x3，x4，x5，x6，x7，x8，x9，x10，x11≥0通过管理运筹学软件，我们可以求得此问题的解如下：x1=8，x2=0，x3=1，x4=1，x5=0，x6=4，x7=0，x8=6，x9=0，x10=0，x11=0，最优值为320。