物理奥赛辅导第十八章真空的恒定磁场
- 格式:doc
- 大小:1.27 MB
- 文档页数:28

第十八章 真空的恒定磁场一、基本要求1、确切理解磁感应强度的概念,明确磁感应强度的矢量性和迭加性;2、掌握毕奥一萨伐尔一拉普拉斯定律,并熟练地运用该定律来计算几何形状比较规则的载流导线所产生的磁场;3、掌握磁场的高斯定理和安培环路定理,并能熟练地运用安培环路定理来计算具有一定对称性分布的磁场的磁感应强度;4、掌握洛仑兹公式和安培定律,掌握计算洛仑兹力、安培力(或磁力矩)的方法。
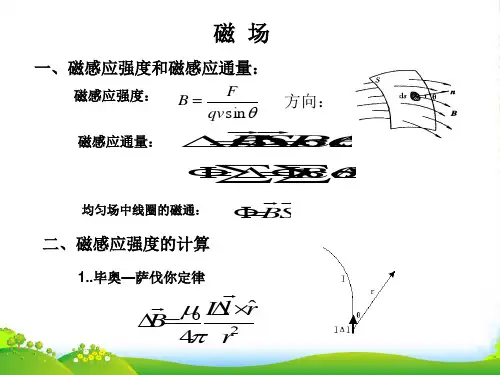
二、基本概念和规律 1.磁感应强度磁场中某点的磁感应强度的大小定义为V q F B 0max / ,即在磁场中某点磁感应强度的大小等于运动试验电荷在该点所受的最大的力F max 与其所带电量q 0和速度的乘积之比值,的方向为置于该点的小磁针北极所指的方向。
应该指出:1)磁感应强度是描写磁场对运动电荷(或电流)施以作用力—磁场力的性质。
它是表征磁场本身性质的物理量。
既与在该点上的运动试验电荷所带的电量和速度无关,又与该点上有无运动试验电荷无关。
2)将磁感应强度和电场强度的定义进行比较,磁感应强度大小不能定义为运动试验电荷在磁场中所受的力与其所带电量和速度乘积之比值,否则的大小不确定;同样,磁感应强度的方向也不能定义为运动试验电荷所受磁场力的方向,不然,的方向亦不确定。
2、毕奥—萨伐尔—拉普拉定律真空中 304rId d ⨯=πμ 应该指出:1)注意电流元→l Id 、矢径→r 方向的规定,→B d 与→l Id 和→r 成右手定则关系。
2)当→l Id 与→r 之间的夹角为零或π,则dB =0,亦即在电流元→l Id 延长线上各点,电流元→l Id 并不产生磁场。
3)磁感应强度的迭加原理载流导线在磁场中某点产生的磁感应强度等于该载流导线上各电流元在该点所产生的磁感应强度的矢量和,即304rrl Id B d B L L⨯==⎰⎰πμ 4)运动电荷所产生的磁感应强度为304r q ⨯=πμ式中q 为运动电荷所带的电量,为其速度。







磁 场一、恒定电流的磁场1、直线电流的磁场通有电流强度为I 的无限长直导线,距导线为R 处的磁感应强度为:RIB πμ20=;如下图距通有电流强度为I 的有限长直导线为R 处的P 点的磁感应强度为:)cos (cos 40βαπμ+=RIB ----------------------------------①若P 点在通电直导线的延长线上,则R=0 α=0 β=π 无法直接应用上述式子计算,可进行如下变换lR d d 21)sin(2121=+βα 上式中1d 、2d 分别为P 点到A 、B 的距离,l 为直导线的长度所以:l d d R )sin(21βα+=代入①式得:)sin(cos cos 4210βαβαπμ++=d d Il B令2sin2cos2cos 2sin 22cos2cos2)sin(cos cos βαβαβαβαβαβαβαβα+-=++-+=++=y将α=0 β=π代入上式得0=y所以:在通电直导线的延长线上任意一点的磁感应强度为0=B2、微小电流元产生的磁场微小电流元的磁场,根据直线电流的磁场公式)cos (cos 40βαπμ+=rIB得:Ⅰ若α、β都是锐角,如左图,有:)cos (cos 40βαπμ+=r I B =)sin (sin 4210θθπμ∆+∆rI因1θ∆、2θ∆0→,所以≈∆+∆=)sin (sin 4210θθπμr I B )(4210θθπμ∆+∆rI所以:θπμ∆=rIB 40Ⅱ若α、β中有一个是钝角,如β(右图),则:]sin )[sin(cos 4)cos (cos 400000θθθθπμβαπμ-+∆=+=r Id I B -------------①00000sin sin cos cos sin sin )sin(θθθθθθθθ-∆+∆=-+∆因0→∆θ,所以:0000cos cos sin sin )sin(θθθθθθθ∆≈∆≈-+∆--------------------------------②②式代入①式得:θπμ∆=rIB40总上所述,电流元I 在空间某点产生的磁场为:θπμ∆=rIB 40,式中r 为电流元到该点的距离,θ∆为电流元端点与该点连线张开的角度。


第十八章 真空的恒定磁场一、基本要求1、确切理解磁感应强度的概念,明确磁感应强度的矢量性和迭加性;2、掌握毕奥一萨伐尔一拉普拉斯定律,并熟练地运用该定律来计算几何形状比较规则的载流导线所产生的磁场;3、掌握磁场的高斯定理和安培环路定理,并能熟练地运用安培环路定理来计算具有一定对称性分布的磁场的磁感应强度;4、掌握洛仑兹公式和安培定律,掌握计算洛仑兹力、安培力(或磁力矩)的方法。
二、基本概念和规律1.磁感应强度 磁场中某点的磁感应强度的大小定义为V q F B 0max / ,即在磁场中某点磁感应强度的大小等于运动试验电荷在该点所受的最大的力F max 与其所带电量q 0和速度的乘积之比值,的方向为置于该点的小磁针北极所指的方向。
应该指出:1)磁感应强度是描写磁场对运动电荷(或电流)施以作用力—磁场力的性质。
它是表征磁场本身性质的物理量。
既与在该点上的运动试验电荷所带的电量和速度无关,又与该点上有无运动试验电荷无关。
2)将磁感应强度和电场强度的定义进行比较,磁感应强度大小不能定义为运动试验电荷在磁场中所受的力与其所带电量和速度乘积之比值,否则的大小不确定;同样,磁感应强度的方向也不能定义为运动试验电荷所受磁场力的方向,不然,的方向亦不确定。
2、毕奥—萨伐尔—拉普拉定律真空中 304rr l Id d ⨯=πμ 应该指出: 1)注意电流元→l Id 、矢径→r 方向的规定,→B d 与→l Id 和→r 成右手定则关系。
2)当→l Id 与→r 之间的夹角为零或π,则dB =0,亦即在电流元→l Id 延长线上各点,电流元→l Id 并不产生磁场。
3)磁感应强度的迭加原理载流导线在磁场中某点产生的磁感应强度等于该载流导线上各电流元在该点所产生的磁感应强度的矢量和,即 304rr l Id B d B L L ⨯==⎰⎰πμ 4)运动电荷所产生的磁感应强度为304r q ⨯=πμ 式中q 为运动电荷所带的电量,V 为其速度。
若运动电荷为正电荷,0>q ,的方向与⨯的方向相同;若运动电荷为负电荷,0<q ,的方向与⨯的方向相反;5)毕一萨一拉定律只在稳恒电流情况下成立。
它是根据大量实验事实进行理论分析的结果,不能从实验上直接加以证明,但由它所计算出的与实验测定相符合,从而间接证明了它的正确性。
它是电流产生磁场所遵循的基本规律,是稳恒磁场的理论基础。
3、稳恒磁场的基本性质1)磁场的高斯定理0·=⎰⎰s d B S即通过任意闭合曲面S 的磁通量等于零。
磁场的高斯定理说明磁场是无源场,磁感应线是闭合曲线。
2)安培环路定理在真空中 ∮L i I l d B ∑=0·μ 即磁感应强度沿任何闭合环路L 的线积分,等于穿过这环路所有电流强度的代数和的0μ倍。
应该指出:a 、在环路定理∮L i I l d B ∑=0·μ中,环路L 上任一点的应是空间中所有电流在该点所产生的磁感应强度的矢量和,即它既包括环路L 内的电流,又包括环路L 外的电流共同产生的。
而i I ∑只包括穿过环路L 的电流。
即是说环路L 外的电流对有贡献,而对沿l 的环流无贡献。
b 、必须注意电流I 的正负规定。
当穿过环路L 的电流方向与环路l 的绕行方向服从右手定则时,I >0,反之I <0。
c 、安培环路定理只对稳恒电流产生的稳恒磁场才成立。
而对于有限长的载有稳恒电流的直导线不能用安培环路定理求磁感应强度,因稳恒电流一定是闭合的,而安培环路定理中的应是闭合电路中全部电流产生的。
d 、无论环路L 外面电流如何分布,只要环路L 内没有包围电流,或者所包围电流强度的代数和为零,则∮L 0·=l d B ,但应当注意,的环流为零,一般并不意味着环路L 上各点的都为零。
e 、安培环路定理说明磁场是非保守场,亦即是有旋场。
4、磁场对运动电荷、载流导线(或载流线圈)的作用1)磁场对运动电荷的作用 运动电荷在磁场中所受的力称为洛仑兹力,由洛仑兹公式计算q ⨯=式中q 为运动电荷所带的电量,V 是它的速度。
洛仑兹力与库仑力是不同的。
主要表现在:a 、洛仑兹力只作用于运动电荷,而库仑力既作用于运动电荷,又作用于静止电荷;b 、洛仑兹力总是垂直于运动电荷的速度,即V F ⊥,所以洛仑兹力只改变运动电荷速度的方向,而不改变其速度的大小,故洛仑兹力对运动电荷不作功。
而库仑力既可改变电荷速度的方向,又可改变其速度的大小,故库仑力对电荷要做功;c 、洛仑兹力与垂直,而库仑力与平行。
在均匀磁场中,带电粒子在洛仑兹力作用下作圆周运动的半径为qB mv R =v 是与相垂直的速度,带电粒子在均匀磁场中运动的回频共振频率mqB T πν21== 它与粒子的速率及回旋半径无关。
2)磁场对载流导线的作用电流元→l Id 在磁场中所受到的安培力→F d 由安培定律计算Id F d ⨯=→ 载流导线所受到的安培为B l Id F L ⨯=⎰→在稳恒电流情况下,载流导线在磁场中运动时,磁力所作的功为∆Φ=I A△Φ是闭合电流回路所包围面积内磁通量的增量。
磁场对载流平面线圈的作用载流平面线圈在均匀磁场中所受的力矩为M m ⨯=→式中NIS m =为载流平面线圈的磁矩。
I 是线圈中的电流强度,N 是线圈的匝数,S 为线圈每匝所包围的面积,的方向与电流I 的方向成右手定则关系。
上式表明,对于任意形状的载流平面线圈(或闭合电路)在均匀磁场中所受合力为零(不考虑线圈变形),但受到一个力矩,这力矩总是力图使这线圈的磁矩m 转到磁感应强度的方向,当m 与的夹角2πθ=时,线圈所受的力矩最大;当0=θ或π时,线圈所受的力矩为零。
当0=θ时,线圈处于稳定平衡状态;πθ=时,线圈处于非稳定平衡状态。
上式只对在同一平面上的任意形状的载流线圈在均匀磁场中成立。
三、解题方法本章的内容分两个方面:一是稳恒电流所产生的磁场;二是磁场对电流(或运动电荷)的作用。
虽然稳恒磁场与静电场的基本性质不同,但分析和处理问题的方法与静电场有很多相似之处。
1、求磁场分布的方法已知电流分布,求磁感应强度的方法有两种。
1)利用毕奥—萨伐尔—拉普拉斯定律和磁场的迭加原理求磁感应强度,即 304r r l Id B L ⨯=→⎰πμ 求 从原则上讲,在已知电流分布的情况下,可利用此种方法求任何载流导体所产生的磁场,因此,这是求的一种普遍方法。
这种方法还应包括利用已知的载流导体的磁感应强度公式和磁场的迭加原理求磁感应强度。
例如将无限长的载流导线弯成几何形状比较规则的各种形状的载流导线(由若干段直线和圆弧组成),在求其它们所产生的磁场时,就是利用载流导线和圆形电流在其圆心处的磁感应强度公式和磁场的迭加原理求。
2)利用安培环路定理求磁感应强度利用安培环路定理求磁感应强度与用静电场的高斯定理求电场强度的方法相类似,其步骤如下:a 、首先分析磁场分布的对称性,这是判断能否用安培环路定理求磁感应强度的关键。
只有当磁场分布具有一定的对称性时,才能用安培环路定理求,否则不能用。
这并不意味着安培环路定理对非对称性磁场不适用,而是用它求不出。
这是因为安培环路定理只是反映了稳恒磁场性质的一个侧面(有旋场),它对磁场性质的描述是不完全的,只有在磁场分布具有高度对称性的情形下,才能根据这种不完全的描述来确定磁场的分布,在一般情况下,应当配合反映磁场性质的另一个侧面(无源场)的高斯定理,才能充分描述稳恒磁场,并由它们确定普遍情形下稳恒磁场的分布。
b 、若能用安培环路定理,则选取适当的闭合环路(又称安培环路)通过拟求的场点,并规定安培环路的绕行方向。
选取安培环路的原则是使B 能从∮L l d B ·中积分号内提出来,以便能算出B ,通常选用的安培环路为圆周和矩形。
c 、分别计算所选取的安培环路的环流和安培环路所包围的电流的代数和,应用安培环路定理求出B ,并指出的方向。
2、磁场对电流、运动电荷的作用1)利用安培定律求磁场对载流导线的作用,即B l Id F L ⨯=⎰→其步骤如下:a 、根据问题的性质,选取适当的坐标系,首先求出在载流导线分布区域内的分布。
若题中已给出的分布,则此步骤求可省略。
b 、将载流导线分成无限多个电流元Id ,利用安培定律,写出某一电流元Id (所在位置不能选得特殊)所受的安培力Id d ⨯=,由右手定则确定d 的方向,然后根据所选择的坐标系将d 沿坐标轴进行正交分解,亦即将d 的矢量式用其分量式表示,以便把矢性函数的运算化成数性函数的运算。
c 、对电流元所受的安培力Fd 的诸分量分别积分,积分遍及整个载流导体。
注意:应根据所选取的坐标系,载流导线的几何形状,电流I 的方向,积分变量正确确定积分上、下限。
载流平面线圈在均匀磁场中所受的力矩,由M m ⨯=→求之,M 和与→成右手定则关系2)磁场对运动电荷的作用 利用络仑兹公式q F ⨯=→求磁场对运动电荷所作用的磁力。
3、常用例题公式1)载流直导线的磁场)(421θθπμCos Cos rI B O -= 式中r 为场点到直导线之垂直距离,1θ为始端电流元方向与其矢径方向之间的夹角。
2θ为末端电流的方向与其矢径方向之间的夹角,的方向由右手定则确定之。
若载流直导线为无限长,即πθθ==21,0,则有rI B O πμ2= 2)载流圆线圈轴线上的磁场23222)(2x R IR B O +=μ式中R 为圆线圈的半径,x 为轴线上的场点到圆线圈的圆心的距离。
当x = 0时,即在圆心处R I B O μ=3)载流长直螺线管内的磁场nI B O μ=式中n 为单位长度的线圈匝数4)载流螺绕环内的磁场当螺绕环横截面积很小时,环的平均周长为l ,则环内的磁感应强度nI I lN B O O μμ== 式中N 为螺绕环的总匝数四、解题示例例1,将一根载流导线弯成如图所示的形状,已知导线中的电流为I ,正方形的边长为a ,圆的半径为R ,求圆心O 点的磁感应强度。
解:利用载流直导线和载流圆线圈圆心处的磁感应强度公式和磁场迭加原理求圆心O 点的磁感应强度。
由于圆心O 点在载流直导线AC 之延长线上,所以载流直导线AC 在O 点产生的磁感应强度B 1=0。
载流圆弧CDE 在O 点产生的磁感应强度B 2是载流圆线圈中心磁感应强度R IO 2μ的43,即RI R IB O O 834322μμ=⨯= 2B 的方向由右手定则可得,垂直于纸面向外。
由于圆心O 点在载流直导线EF 延长线上,所以载流直导线EF 在O 点产生的磁感应强度B 3=0。
由载流直导线的磁感应强度公式可得载流直导线FG 在O 点产生的磁感应强度为:a I Cos Cos a I B O O πμπππμ82)432(44=-= 4B 的方向垂直于纸面向外,同理可得载流直导线GA 在O 点产生的磁感应强度为a I Cos Cos a I B O O πμπππμ82)24(45=-= 5的方向垂直于纸面向外,选取通过O 点垂直于纸面向外为正方向,由磁场的迭加原理得圆心O 点的磁感应强度为aI R I B B B B B B O O μμ28354321+=++++= 的方向垂直于纸面向外。