当前位置：文档之家 › 2020年高中物理奥赛辅导PPT★★运动学教学课件

2020年高中物理奥赛辅导PPT★★运动学教学课件

  • 格式：ppt
  • 大小：3.59 MB
  • 文档页数：65

下载文档原格式

  / 65

合集下载

2020年高中物理奥林匹克竞赛辅导课件★★01质点运动学(B位移 速度 加速度)优秀课件PPT

2020年高中物理奥林匹克竞赛辅导课件★★01质点运动学(B位移 速度 加速度)优秀课件PPT

谢谢观看！
用微笑告诉别人，今天的我，比昨天更强。瀑布跨过险峻陡壁时，才显得格外雄伟壮观。勤奋可以弥补聪明的不足，但聪明无法弥补懒惰的缺陷。孤独是 每个强者必须经历的坎。有时候，坚持了你最不想干的事情之后，会得到你最想要的东西。生命太过短暂，今天放弃了明天不一定能得到。只有经历人生 的种种磨难，才能悟出人生的价值。没有比人更高的山，没有比脚更长的路学会坚强，做一只沙漠中永不哭泣的骆驼！一个人没有钱并不一定就穷，但没 有梦想那就穷定了。困难像弹簧，你强它就弱，你弱它就强。炫丽的彩虹，永远都在雨过天晴后。没有人能令你失望，除了你自己人生舞台的大幕随时都 可能拉开，关键是你愿意表演，还是选择躲避。能把在面前行走的机会抓住的人，十有八九都会成功。再长的路，一步步也能走完，再短的路，不迈开双 脚也无法到达。有志者自有千计万计，无志者只感千难万难。我成功因为我志在成功！再冷的石头，坐上三年也会暖。平凡的脚步也可以走完伟大的行程。 有福之人是那些抱有美好的企盼从而灵魂得到真正满足的人。如果我们都去做自己能力做得到的事，我们真会叫自己大吃一惊。只有不断找寻机会的人才 会及时把握机会。人之所以平凡，在于无法超越自己。无论才能知识多么卓著，如果缺乏热情，则无异纸上画饼充饥，无补于事。你可以选择这样的“三 心二意”：信心恒心决心；创意乐意。驾驭命运的舵是奋斗。不抱有一丝幻想，不放弃一点机会，不停止一日努力。如果一个人不知道他要驶向哪个码头， 那么任何风都不会是顺风。行动是理想最高贵的表达。你既然认准一条道路，何必去打听要走多久。勇气是控制恐惧心理，而不是心里毫无恐惧。不举步， 越不过栅栏；不迈腿，登不上高山。不知道明天干什么的人是不幸的！智者的梦再美，也不如愚人实干的脚印不要让安逸盗取我们的生命力。别人只能给 你指路，而不能帮你走路，自己的人生路，还需要自己走。勤奋可以弥补聪明的不足，但聪明无法弥补懒惰的缺陷。后悔是一种耗费精神的情绪，后悔是 比损失更大的损失，比错误更大的错误，所以，不要后悔！复杂的事情要简单做，简单的事情要认真做，认真的事情要重复做，重复的事情要创造性地做。 只有那些能耐心把简单事做得完美的人，才能获得做好困难事的本领。生活就像在飙车，越快越刺激，相反，越慢越枯燥无味。人生的含义是什么，是奋 斗。奋斗的动力是什么，是成功。决不能放弃，世界上没有失败，只有放弃。未跌过未识做人，不会哭未算幸运。人生就像赛跑，不在乎你是否第一个到 达终点，而在乎你有没有跑完全程。累了，就要休息，休息好了之后，把所的都忘掉，重新开始！人生苦短，行走在人生路上，总会有许多得失和起落。 人生离不开选择，少不了抉择，但选是累人的，择是费人的。坦然接受生活给你的馈赠吧，不管是好的还是坏的。现在很痛苦，等过阵子回头看看，会发 现其实那都不算事。要先把手放开，才抓得住精彩旳未来。可以爱，可以恨，不可以漫不经心。我比别人知道得多，不过是我知道自己的无知。你若不想 做，会找一个或无数个借口；你若想做，会想一个或无数个办法。见时间的离开，我在某年某月醒过来，飞过一片时间海，我们也常在爱情里受伤害。1、 只有在开水里，茶叶才能展开生命浓郁的香气。人生就像奔腾的江水，没有岛屿与暗礁，就难以激起美丽的浪花。别人能做到的事，我一定也能做到。不 要浪费你的生命，在你一定会后悔的地方上。逆境中，力挽狂澜使强者更强，随波逐流使弱者更弱。凉风把枫叶吹红，冷言让强者成熟。努力不不一定成 功，不努力一定不成功。永远不抱怨，一切靠自己。人生最大的改变就是去做自己害怕的事情。每一个成功者都有一个开始。勇于开始，才能找到成功的 路。社会上要想分出层次，只有一个办法，那就是竞争，你必须努力，否则结局就是被压在社会的底层。后悔是一种耗费精神的情绪后悔是比损失更大的 损失，比错误更大的错误所以不要后悔。每个人都有潜在的能量，只是很容易:被习惯所掩盖，被时间所迷离,被惰性所消磨。与其临渊羡鱼，不如退而结网。 生命之灯因热情而点燃，生命之舟因拼搏而前行。世界会向那些有目标和远见的人让路。不积跬步，无以至千里；不积小流，无以成江海。骐骥一跃，不 能十步；驽马十驾，功在不舍。锲而舍之，朽木不折；锲而不舍，金石可镂。若不给自己设限，则人生中就没有限制你发挥的藩篱。赚钱之道很多，但是 找不到赚钱的种子，便成不了事业家。最有效的资本是我们的信誉，它小时不停为我们工作。销售世界上第一号的产品——不是汽车，而是自己。在你成

2020年高中物理奥林匹克竞赛辅导课件★★01质点运动学(B位移 速度 加速度)最新课件PPT

2020年高中物理奥林匹克竞赛辅导课件★★01质点运动学(B位移 速度 加速度)最新课件PPT
两v 矢v 量a a 相 互v ( 垂c 直a R 时s o 应有st 0i i n R ct j o ) s
( 2 R co t i s 2 R si t j) n
0 va 得证
[例2]:
v 2t一2。质点在(1x)写Oy出平质面点内任运意动时，刻运的动位方r置程矢为量x=2，t速，度y=矢19量-
t1 0s t2 3s t3 3s (舍去)
[例3]如图,长为l的细棒,在竖直平面内沿墙角下滑,上端A
下滑速度为匀速v。当下端B离墙角距离为x (x<l)时,B端
水平速度和加速度多大? 解：建立如图所示的坐标系
y A
设A端离地高度为y
x2y2 l2
yl
方程两边对t求导
2xdx2ydy0 dt dt
讨论：
a. 路程：质点沿轨迹运动所经历的路径长度 s
bcd...在路即单极程方限是向r情标直况量线下，运s大动小时d 与r位移r的d大s 小s一般不相等，
二.速度： 描述质点运动快慢和运动方向的物理量
1。平均速度
v
r
xiyjzk
t t t t
vxivyjvzk
大小：
v
r t
方向：r 的方向
谢谢观看！
努力，未来老婆的婚纱都是租的。只有你的笑才能让你在 中找到光明。我受过的伤都是我的勋章。知世故而不世故 良的成熟。愿你早日领教过这世界深深的恶意，然后开启 谁的快意人生。第二名就意味着你是头号输家——科比·布 当你感觉累的时候，你正在走上坡路。如果每个人都理解 得普通成什么样。赚钱的速度一定要超过父母变老的速度 发现以前的自己是个傻逼的过程，就是成长。脾气永远不 事。你那能叫活着么？你那“你如今的气质里，藏着你走 读过的书，和爱过的人。”素质是家教的问题，和未成年 总会有人是第一，那为什么不能是我？你可以没钱没颜， 以不努力。如果今天我取得了成功，一定是昨天我拼上了 阳光里做个孩子风雨里做个大人。枯木逢春犹再发，人无 年世界那么大，我要赚钱带父母去看看人情世故要看透， 不能丢。所有的人都在努力，不是只有你受尽委屈爱情可 质，但生活不行你才二十岁，你可以成为任何想成为的人 像一杯茶，不会苦一辈子，但总会苦一阵子。中学时候本

高中物理奥林匹克竞赛专题质点运动学(共37张)PPT课件

高中物理奥林匹克竞赛专题质点运动学(共37张)PPT课件

dt
v 0 2v 2 v 0 4 i 1j2
av022i6j
t
例：一质点由静止开始作直线运动，初始加速度为a0， 以后加速度均匀增加，每经过τ秒增加a0，求经过t秒
后质点的速度和运动的距离。
解：据题意知，加速度和时间的关系为：
a
a0
a0
t
a dv dt
dvadt
(直线运动中可用标量代替矢量）
v0 ta d0 t(ta 0a 0t)d ta 0 t2 a 0t2 vdx dxvdt dt
x0 tv d0 t(a t0 t 2 a 0t2 )d ta 2 0t2 6 a 0t3
d
2
r
dt 2
ax
dvx dt
d2x dt2 ,
ay
dvy dt
d2y dt2 ,
az
dvz dt
d2z dt2
a ax2ay2az2
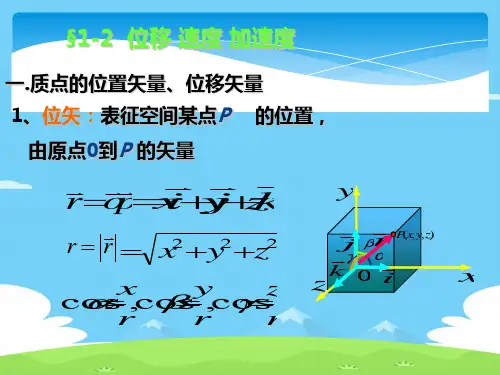
描述 质 点运动的四个基本物理量：r,r,v,a
r, v 描述质点在某一时刻所处的状态，称为质点
运动的状态参量。
r表示t时间内质点位置的变化， a为速度的瞬
在运动方程中，消去t即得轨道方程：f(x,y，z)=0。
1.2.2 位移 路程
1.位移
t时刻，A点位矢为 r1
t+Δt时刻在B点位矢为 r2
z
A
r
B
r1
r2
o
y
x
在t 时间内，位矢的变化量（即A到B的有向线
段）称为位移。
AB位移：rr2 r1
在直角坐标系中：rr2r1 xi yj zk
vx , vy
vx
, vz
dx dt
为速度在x，y，z方向的分量。

2020年高中物理竞赛(力学篇)02运动、力学定律：动能定理(共17张PPT)

2020年高中物理竞赛(力学篇)02运动、力学定律：动能定理(共17张PPT)

重力势能（以地面为零势能点）
0
势
EP
mgdy mg(0 y) mgy
y
能 只
弹性势能（以弹簧原长为零势能点）
具
E p
0
kx
• dx
(0
1
kx2 )
1
kx 2
x
2
2
有 相
引力势能（以无穷远为零势能点）
对
意
EP＝
－G
r
Mm r 2 dr
GMm
1 r
义
质点在某一点的势能大小等于在相应的保守力的作用
U(x)
E3 •d
E2 E1
A a
••
b• C B •c
X
E=E1 E=E2 E=E3
系统被限制在势阱A中运动 系统在势阱A或C中运动，且二者只居其一。 系统可在x≥xd的区域自由运动。
例 一个质量为m的小球，
由一根长为 l的细杆连接
成摆。可在竖直平面内绕 O点自由摆动或转动。 细杆质量忽略不计。
Af
(G0
Mm ra
)
(G0
Mm )
rb
As
1 2
kxa2
1 2
kxb2
A保
ab
F保
• dr
E pa E pb
DE p
保守力做正功等于相应势能的减少； 保守力做负功等于相应势能的增加。
比
A
1 2
mv 22
1 2
mv
2 1
E KB
E KA
DEK
较 外力做正功等于相应动能的增加；
外力做负功等于相应动能的减少。
力总是指向平衡位置
U(x) A a••

2020年高中物理奥赛辅导PPT★★运动学优品课件PPT

2020年高中物理奥赛辅导PPT★★运动学优品课件PPT

( third order determinant)
两矢量所在平面
A
2
a A
1
i
j
k
A
2
x 1 y1
z运位动置的物矢理量量
parameters for describing particle motion
1
位置矢量 r position vector
（其z单为矢量k为
z
P
z (t1)
P1
(t2)
P2
r1
r2
平均速率 v
O
mean speed
v
rs rt
是标量
X
Y
显然 v v
当rt 时0 ，平均速度v 的极限值具有更重要的意义：
瞬时速度简称 insvtaenlotacniteyous
v速el度oc瞬ityv时速z度当Prdt
0时 v
d
v rlti m0 rt d 方向：为 极限方向
两矢量叉乘的结果是矢量
A
A 的方向
1
2
大小 A
A
1
2
sin A A
a
12
方向 垂直于两矢量决定的平面，指向
按右螺旋从叉号前的矢量沿小于
p 角转向叉号后矢量的旋进方向。
若 A A 的空间坐标式为
、1
2
A
1
+ + x 1 i
y1j
z1k
A
2
+ + x 2 i
y2j
z2k
A
1
A A 用一个三阶行列式
1
2
表示
点（标）(乘scalar multiplication)

2020山大附中高中物理竞赛辅导课件01质点运动学(共12张PPT)

2020山大附中高中物理竞赛辅导课件01质点运动学(共12张PPT)
2 、选择一条适合自己的路坚持走下去，只要坚持，就会取得成功。 1 、想急于得到所需的东西，一时冲动，草率行事，就会身遭不幸。遇事时要多动脑，多思考，才能成功。 2 、在人生中只有曲线前进的快乐，没有直线上升的成功。只有珍惜今天，才会有美好的明天;只有把握住今天，才会有更辉煌的明天! 4 、工作上的烦恼，不要带回家，解决不了任何问题，带回来会平添更多烦恼。 5 、一个人要想掌握精湛的技术，不能性急，要肯于吃苦，扎扎实实地练好基本功。 6 、大成若缺，其用不弊。大盈若冲，其用不穷。大直若屈，大巧若拙，大辩若讷。 6 、遇难心不慌，遇易心更细。 13 、一个能从别人的观念来看事情，能了解别人心灵活动的人，永远不必为自己的前途担心。 5 、在你往上爬的时候，一定要保持梯子的整洁，否则你下来时可能会滑倒。 12 、一个人要实现自己的梦想，最重要的是要具备以下两个条件：勇气和行动。 18 、金矿的山上还有着其他花朵，除了具备发现的眼睛外，还需要有着肯流汗的心。成功提示：金子常常就埋在身旁的泥土里，勤奋是最好 的点金指。
如：地球绕太阳的运动、轨道运动
b. 物体无转动运动时可视为质点 物体上任一点都可以代表物体的运动
三.坐标系 确定物体相对参照系的位置，需在参照系上建立坐标系
1.直角坐标系：
直角坐标 (x,y,z)确定质点位置
y
k
z
j
P(x, y,z)
y
i
0z x x
2.自然坐标系
在已知运动轨迹上任选一点0为原点建立的坐标系
14 、男人最大的武器是眼神，女人最大的武器是眼泪。 4 、工作上的烦恼，不要带回家，解决不了任何问题，带回来会平添更多烦恼。 9 、眼泪不是我们的答案，拼搏才是我们的选择。 7 、每个行业都是这样：很多当年的第一名都已销声匿迹，曾经默默无闻的，却成了领军人。真正的事业拼得都不是快功。成功大多是慢火细 熬出来的。你可以不是第一，但一定要最后一个放弃。

2020山大附中高中物理竞赛辅导课件01质点运动学(共12张PPT)

2020山大附中高中物理竞赛辅导课件01质点运动学(共12张PPT)

自然坐标 s(t) 确定质点的位置 et :切向单位矢量
en :法向单位矢量
3.平面极坐标系
Ox：极轴 r：极径
： 辐角
0
s
en
P
et
P(r,) r(t)
0
x
※通常规定从极轴沿逆时针方向的 为正 ※平面极坐标( r, ) 确定质点的位置
THE END 祝大家竞赛顺利、学业有成
谢谢观看！
13. 生活坏到一定程度就会好起来的，因为它无法更坏。 1. 驾驭命运的舵是奋斗。不抱有一丝幻想，不放弃一点机会，不停止一日努力。 9. 你若一向在、我便一向爱。惋惜没人会懂我的。 4. 正是这些平凡的人生，却构成了伟大的历史。 3. 路曼曼其修远兮，吾将上下而求索。 14. 漫无目的的生活就像出海航行而没有指南针。 9. 只有一条路不能选择——那就是放弃的路;只有一条路不能拒绝——那就是成长的路。 15. 在人的一生中，可能会遇到各种各样的困难和挫折，也就是大家常说的逆境。逆境不是愉快的，但逆境并不能因为我们不喜欢就不到来。 我们应该充分利用逆境，抓紧时间学习。等逆境过后，见到自己的进步和收获，意义不同寻常。——夏承寿 5. 如果在胜利前却步，往往只会拥抱失败;如果在困难时坚持，常常会获得新的成功。 8. 赚钱之道很多，但是找不到赚钱的种子，便成不了事业家。 15. 伟人所达到并保持着的高处，并不是一飞就到的，而是他们在同伴们都睡着的时候，一步步艰辛地。 12. 当你能飞的时候就不要放弃飞;当你有梦的时候就不要放弃梦。 3. 崇高的理想就像生长在高山上的鲜花。如果要搞下它，勤奋才能是攀登的绳索。 5. 有理想在的地方，地狱就是天堂。 20. 可以失败。可以哭闹。但是不能失去对自己的勇气和信心。 4. 伤害你最深的人，往往是那些声称永远不会伤害你的人。 12. 要纠正别人之前，先反省自己有没有犯错。

高中物理奥林匹克竞赛——质点运动学(共38张PPT)

高中物理奥林匹克竞赛——质点运动学(共38张PPT)

x t 2 (SI)
y t 4 2t 2 (SI)
dx
t 2
vx dt 2t
vx 4ms
v y ddy t4t 34t t
v 4 i 2j4 m /s
2
v
vy 24ms
vx 2v2 y 437 ms
axddx vtd d22 x t 2ms2 练习 a y ? ay1t2 244(m 42)s
六、质点运动学的两类问题
已知运动方程，求质点的速度和加速度 求导数
已知质点的速度(或加速度)和初始条件， 求质点运动方程及其它未知量
运用积分方法
例：一质点运动轨迹为抛物线
x t 2 (SI) y t 4 2t 2 (SI)
y
求：x= -4m时（t>0)
x
粒子的速度、速率、 加速度。
解：
x ( t) i y ( t) j z ( t) k
Z
P(x,y,z) r
分量式 x x(t ) y y(t) z z(t)
k
iO
j
z x
Y
y
X
轨道
质点运动的空间轨迹称为轨道.
轨道方程: F(x,y,z)0
三、位移
位移矢量:在t时间间隔内位矢的增量
r r 2 r 1 r ( t 2 ) r ( t 1 )
t
t2t1
· r1
瞬时加速度
o
a (t) lt i0m vtd dvtd d2r2 t
加速度是速度对时间的一阶导数
v1 B
· v2
r2
v1 Δv
v2
或位矢对时间的二阶导数
直角坐标系中
加速度
a dv dxv idyv jdzv k dt dt dt dt

2020年高中物理奥林匹克竞赛辅导课件★★01质点运动学(C直线运动 圆周运动及其描述)

2020年高中物理奥林匹克竞赛辅导课件★★01质点运动学(C直线运动 圆周运动及其描述)

已知运动方程 x x，(求t)速度和加速度
速度 v dxdt
----微分问题
加速度 a dvdt d2x dt2
已知加速度a=a(t)和初始条件，求速度、位移和运动方程
a dv dvadt ----积分问题
dt
v
t
两边积分 dv adt
vo
o
t
vv0
adt
0
t
v v0
adt
0
a为常数时 vv0 at (1)
40
2w 2 tw 205ra/sd 2
N 20圈 2
THE END 祝大家竞赛顺利、学业有成
遇到困难时不要放弃，要记住，坚持到底就是胜利。 学会下一次进步，是做大自己的有效法则。因此千万不要让自己睡在已有的成功温床上。 读书是在别人思想的帮助下，建立起自己的思想。——鲁巴金 我们必须拿我们所有的，去换我们所没有的。 每个企业家都有自己的特色和风格，但他们还有共同的特征，那就是：有正确的判断力，有决心，敢于创新，勤奋工作。 为你制造一些困难和障碍的人未必是你的敌人，把你从困境里拉出来的人未必是你的朋友。不要用眼前的利益得失看人，要看长远，所谓路遥 知马力，日久见人心！ 上天不会亏待努力的人，也不会同情假勤奋的人，你有多努力时光它知道。 不能强迫别人来爱自己，只能努力让自己成为值得爱的人。 泉水，奋斗之路越曲折，心灵越纯洁。 每一种创伤，都是一种成熟。 所谓“人”，就是你在它上面再加上任何一样东西它就不再是“人”了。 要求别人是很痛苦的，要求自己是很快乐的。
身体健康，学习进步！
又 v dx
dxvdt
dt
x
t
t
dx vdt
x0
0
即
x x0

2020年高中物理竞赛辅导课件(运动的守恒定律)02机械能守恒定律(共17张PPT)

2020年高中物理竞赛辅导课件(运动的守恒定律)02机械能守恒定律(共17张PPT)
解：(1)船－砂袋系统：P水平=const.
mv0=(m+M)v
v= mv0/(m+M)
(2)牛Ⅱ： kv (m M ) dv dt
kvdx (m M ) dv dx dt
S
k
0
dx dv
0 mM
v
k S v mv0
mM
mM
S mv0 / k
[思考] ①系统在碰撞前后动能变否？ ② 一起运动过程中 v(t)=? x(t)=?
*§3.5 质心 (The Center of Mass) 1.质心定义
——质点系中一个特殊的点，其位矢为
rc
mi ri
i
mi
i
z
ri
mi
rc
C y
xO
2.质心运动定理
Fext
Mac
合外力 系统总 质心加 质量 速度
Note: 用牛Ⅱ处理大块物体的平移运动， 其实是用质心运动定理处理质心的 运动．
所有外力 所有内力 系统总动能 做的功 做的功 的增量 [来历] 将质点的动能定理应用于系统中各质
点，求和．
2.功能原理(work-mechanical energy theorem)
Aext Anon (Ek E p )
所有外力 所有非保守 系统机械能 做的功 内力做的功 的增量
[来历] Aext Aint Ek
其中 Aint Anon Acon Anon (Ep )
于是 ……
w of conservation of mechanical energy
若 Aext Anon 0
则 Ek Ep const.
Notes: ⑴动能定理、功能原理和机械能守 恒定律都只是在惯性系中成立．
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

自然坐标系
自然坐标系
t 时刻位置 M
初始位置
法向N
质点的运动学方程s s( t )， 速率 v
d d
s t
速度加速度
自然坐标系时t 刻位置 M
自然坐标 中的 速度 和 加速度
( third order determinant)
两矢量所在平面
A
2
a A
1
i
j
k
A
2
x 1 y1
z
1
x 2 y2
z2
描述质点运位动置的物矢理量量
parameters for describing particle motion
1
位置矢量 r position vector
（其z单为矢量k为
z
P
称为
参 数方程
x y z
xyz(((ttt)))
即 运动学方程可表成
r x(t)i +y(t)j +z(t)k
所从得参的数空方间程曲中线消方t去程
O
x
称f为(x,轨y,迹z)方0程
X
z r
y Y
位移
3
位 移 rr displacement
rr r2 r1
+(ry22 ry11)j(+x2(z2x1)zi1)k
两矢量叉乘的结果是矢量
A
A 的方向
1
2
大小 A
A
1
2
sin A A
a
12
方向 垂直于两矢量决定的平面，指向
按右螺旋从叉号前的矢量沿小于
p 角转向叉号后矢量的旋进方向。
若 A A 的空间坐标式为
、1
2
A
1
+ + x 1 i
y1j
z1k
A
2
+ + x 2 i
y2j
z2k
A
1
A A 用一个三阶行列式
1
2
表示
d r
（曲线上P点的切线方向）
在直角坐标中
d
vd
xd
d
i+
ddyj
+
zddBiblioteka kOYvxi +vyj +vzk
X
的v 大小称为s速pe率ed v v vx2+ vy2+ vz2
而且当rt 0时rr 故 v rltim0 rst
rs
d d
s
平均加速度
5 加速度
怎a样cce定le量rat描ion述 平均加速度a m质ean点a的cc速ele度ati随on
A
2
a
A
1
A
+ A A 服从平行四边形法则
1
2
A
A 为邻边 A 为对角线
、 1
2
若A
( + ( + ( + ( x 1
x2
i
y1
y
j
2
则A
( ( + ( ( x 1
x
2
i
y1
y
j
2
A
A
+( ( A 1
A
2
2
A 反向为 A 减法相当于将一矢量反向后再相加。
2
2
矢量乘法
矢量乘法 ( vectorial multiplication)
点（标）(乘scalar multiplication)
两矢量的点乘 = 两量大小与它们夹角余弦的乘积
A
2
a
A
1
A
2
cos A
A
a
12
两矢量点乘的结果是标量
在直角坐标中
A
1 等于对应坐标乘积的代数和
O
例如 A
A
1
2
+ x 1 x 2
y1
y
2
叉（矢）乘( cross叉mu乘ltiplication)
）
r x i + yj + zk
gr
r 的大小为
O
b
y
其r单位x是2+米y2（+zm2)（其xX 单为a矢量（i为其单）为矢量Yj为
其三个方向余弦为
cos a x r cos b y r cos g z r
2
运动学方程
运动学方程
z
kinematic equation
r r (t)
间r 随变时化
其投影式
运动第学一章
2020年高中物理奥赛辅导PPT★★
第一节质点质点参运考动系的描述
moraspsaprtoicinlet reference system
质点
忽略物体的形状和大小，保留物体
原质量的一ss 个1理- 1想化的物理点模型。
参考系 为确质定点物运体动的的位描置述和描述物体运动
Des而cr被ipt选io作n 参of考pa的rt物ic体le或m物ot体io群n 。
坐标系 coordinate system
固联在参考系上的正交数轴组成的系统，可定量描 述物体的位置及运动。如直角坐标系、自然坐标系等。
z
坐标系 θ 卫星
r 球坐标系
坐标系（直角坐标系）
O
Y
X 参考系（地面）
运动质点
切线
法线
n
τ
φ参考系（地心）
自然坐标系
由运动曲线上任 一点的法线和切 线组成
质点运矢动量的知描识述
z (t1)
P1
(t2)
P2
r1
r2
O
rr rx i +ryj +rzk
Y
(
一位般实移：际的r路s大程小rrrr，rs特殊PP11PP：22r在单t 直向X时0线，r运s动r视r中r 为s 相r等r 。
平均速度
4 怎样描速述度质点 velocity
快v 位慢m平rr置程ea均rtn变度方速v化及e向度l是o的方c与矢ri向tvyr量相？同
j
A
0i
xX
i 、j 分别为 X、Y 轴的
单位矢量（大小为1，方向
分别沿 X、Y 轴正向）。
印刷
A = x i +yj
在课本中惯用印刷形式。 在本演示课件中，为了 配合同学做手书作业，采 用手书形式。
矢量的基本运(f算undam矢en量tal 加ope法rations of vectors
矢量加法 ( vectorial addition)
a
rltim0
v rt
d d
v
d2 d2
方向：为rt 0 时
v 极限方向。 在直角坐标系中
r1
t1P1 当rt 0 v
d
P2
tv2
a ddvx i + ddvyj + ddvz k
r2
dd2x2
i+
d2y d2
j
+
d2z d2
k
O
ax i + ayj +azk X
a 的大小v a ax2+ ay2+az2 Y
z (t1)
P1
(t2)
P2
r1
r2
平均速率 v
O
mean speed
v
rs rt
是标量
X
Y
显然 v v
当rt 时0 ，平均速度v 的极限值具有更重要的意义：
瞬时速度简称 insvtaenlotacniteyous
v速el度oc瞬ityv时速z度当Prdt
0时 v
d
v rlti m0 rt d 方向：为 极限方向
a
v2 v1 rv 时间t2的变t1化？rt
z
v
P1tv1
vv1
的质大点r1小速和度方v 向v2
P2
t2 v
vv2
a 的方向与rv 一致 随时都在改r2 变。
当rt 时0，平均加速度 O
的极限值具有更重要的意义：
a
X
Y
瞬时加速度
瞬时加速简度称加速度 a z inacstcaenletarnateioounsacceleration
description of a particle motion
矢量基本知识
矢量 (vector)
有大小、有方向，且服从平行四边形运算法则的量。
线段长度（大小）；箭头（方向）。
A
手书
A （附有箭头）
印刷
A （用黑体字，不附箭头）
在 X-Y 平面上的某矢量矢A量表示该矢式量 A 的坐标式
Y
y
手书
A = xi +yj