振动理论第四讲 简谐振动中的能量

§3-3简谐振动的能量下面以弹簧振子为例来说明简谐振动的能量。

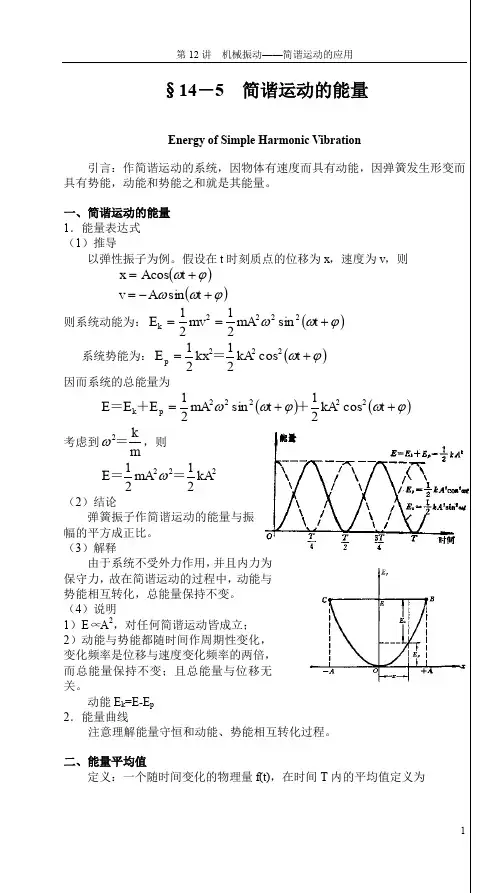
某一时刻 t ：位移 ()0c o s x A t ωϕ=+ 速度 ()0s i n v A t ωωϕ=-+振动动能 ()2222011sin 22k E mv m A t ωωϕ==+ ()2201sin 2kA t ωϕ=+振动势能 ()222011cos 22p E kx kA t ωϕ==+ 总能量 22221122k p E E E kA m A A ω=+==∝ 振幅反映了振动的强度 简谐振动系统机械能守恒！动能和势能相互转化。

简谐振动的系统都是保守系统。

动能和势能在一个周期内的平均值为()2220001111()sin 24T T k k E E t dt kA t dt kA T T ωϕ==+=⎰⎰ ()2220001111()cos 24T T p p E E t d t kA t dt kA T T ωϕ==+=⎰⎰21142k p E E kA E ===动能和势能在一个周期内的平均值相等，都等于总能量的一半。

例3.4：见第一册教材第113页。

（不讲）例：光滑水平面上的弹簧振子由质量为 M 的木块和劲度系数为 k 的轻弹簧构成。

现有一个质量为 m ，速度为 0u 的子弹射入静止的木块后陷入其中，此时弹簧处于自由状态。

（不讲） （1）试写出谐振子的振动方程；Ox（2）求出2Ax =-处系统的动能和势能。

解：（1）射入过程，水平方向动量守恒。

设射入后子弹和木块的共同速度为 0V ()00mu M m V =+00mV u M m=+ 建立坐标系如图，初始条件为00x =， 00v V = 谐振系统的圆频率为ω=初相位 032ϕπ=振幅v A ω===振动方程3o 2x π⎫=+⎪⎪⎭（2）势能 ()22220112228p m u A E kx k M m ⎛⎫=== ⎪+⎝⎭O动能 ()22222031132888k p m u E E E kA kA kA M m =-=-==+Ex ：质量为kg 10103-⨯的小球与轻弹簧组成的系统，按)SI ()328cos(1.0ππ+=t x 的规律作谐振动，求：(1)振动的周期、振幅和初相位及速度与加速度的最大值；(2)最大的回复力、振动能量、平均动能和平均势能，在哪些位置上动能与势能相等?(3)s 52=t 与s 11=t 两个时刻的相位差； 解：(1) 0.1m,8A ωπ== rad/s ， 214T πω∴==秒， 02/3ϕπ= πω8.0==A v m 1s m -⋅ 51.2=1s m -⋅ 2.632==A a m ω2s m -⋅ (2) 0.63N m m F ma ==J 1016.32122-⨯==m mv E J 1058.1212-⨯===E E E k p当p k E E =时，有p E E 2=，即 )21(212122kA kx ⋅=∴ m 20222±=±=A x (3) ππωφ32)15(8)(12=-=-=∆t t§3-4简谐振动的合成一、两个同向同频简谐振动的合成设质点同时参与两个同方向同频率的谐振动 ()1110c o s x A t ωϕ=+()2220c o s x A t ωϕ=+质点的合位移()()12110220c o sc o sx x x A t A t ωϕωϕ=+=+++下面我们用旋转矢量法求合位移：0t = 时刻，两分振动与 x 轴正方向的夹角分别为 10ϕ 和 20ϕ，以相同的角速度 ω 逆时针转动。

振动能量计算公式1. 简谐振动能量。

- 对于一个弹簧振子做简谐振动，其动能E_k=(1)/(2)mv^2，其中m是振子的质量，v是振子的速度。

- 根据简谐振动的速度公式v = ω Asin(ω t+φ)（ω是角频率，A是振幅，φ是初相位），则动能E_k=(1)/(2)mω^2A^2sin^2(ω t + φ)。

- 其势能E_p=(1)/(2)kx^2，对于简谐振动x = Acos(ω t+φ)，所以E_p=(1)/(2)kA^2cos^2(ω t+φ)。

- 弹簧振子的总能量E = E_k+E_p，由于k = mω^2，将E_k和E_p表达式代入可得：- E=(1)/(2)mω^2A^2sin^2(ω t+φ)+(1)/(2)mω^2A^2cos^2(ω t+φ)- 根据sin^2α+cos^2α = 1，所以E=(1)/(2)mω^2A^2（总能量守恒，与时间t 无关）。

2. 阻尼振动能量。

- 阻尼振动的能量是逐渐减小的。

- 阻尼振动的能量E(t)=E_0e^ - (2β t)/(m)，其中E_0是初始能量，β是阻尼系数，m是振子质量，t是时间。

3. 受迫振动能量。

- 在稳定状态下，受迫振动的能量取决于驱动力的功率。

- 设驱动力F = F_0cos(ω_dt)，振子做受迫振动达到稳定时的振动方程为x = Acos(ω_dt+φ)。

- 驱动力的功率P = Fv，其中v=-Aω_dsin(ω_dt + φ)，则P=-F_0Aω_dcos(ω_dt)sin(ω_dt+φ)。

- 在一个周期T=(2π)/(ω_d)内的平均功率¯P=(1)/(T)∫_0^TPdt，通过计算可得¯P=(1)/(2)F_0Aω_dsinφ。

- 受迫振动系统的能量与平均功率有关，能量E=¯Pt（t为时间），在稳定状态下能量保持稳定。

简谐振动的能量公式好嘞，以下是为您生成的关于“简谐振动的能量公式”的文章：咱先来说说啥是简谐振动。

比如说一个小球挂在弹簧上，一松手，小球就这么上上下下地动起来，这就是简谐振动。

简谐振动的能量可是有讲究的，这里面的能量公式啊，能让咱们清楚地知道这个振动系统里到底藏着多少能量。

简谐振动的能量主要包括动能和势能。

动能呢，就好比那个上蹿下跳的小球跑起来的能量；势能呢，就像被拉长或者压缩的弹簧储存的能量。

那简谐振动的能量公式到底是啥呢？E = 1/2 kA²，这里的 E 表示总能量，k 是劲度系数，A 是振幅。

咱来好好琢磨琢磨这个公式。

振幅 A 越大，就意味着振动的幅度越大，那总能量也就越大。

这就好像荡秋千，荡得越高，也就是振幅越大，需要的能量就越多。

我记得有一次在课堂上给学生们讲这个知识点。

当时我拿了一个小弹簧和一个小铁球做演示。

我把弹簧拉长，然后松手让铁球振动起来，同学们都瞪大眼睛看着。

我问他们：“你们觉得这个铁球振动的能量和什么有关？”有的同学说和弹簧拉得长短有关，有的说和铁球的重量有关。

我笑着摇摇头，然后开始给他们讲解这个能量公式。

我告诉他们，就像这个弹簧，拉得越长，振幅越大，能量也就越大。

然后我又改变了弹簧的劲度系数，让他们观察铁球振动的变化。

同学们一下子就明白了，那一张张恍然大悟的小脸，让我特别有成就感。

咱们再回到这个公式。

劲度系数 k 越大，同样的振幅下，能量也会越大。

这就好比是不同的弹簧，有的硬一些，有的软一些，硬的弹簧储存的能量相对就更多。

在实际生活中，简谐振动的例子可不少。

像钟摆的摆动，吉他弦的振动，甚至是我们的心脏跳动，都可以用简谐振动的原理和能量公式来解释。

比如说吉他弦，调弦的时候，改变弦的松紧程度，其实就是在改变劲度系数。

弦调得越紧，劲度系数越大，振动的能量就会有所变化，发出来的声音也就不同啦。

还有啊，心脏的跳动也是一种简谐振动。

当我们运动的时候，心跳会加快加强，振幅和频率都发生变化，能量的供给也得跟上，不然咱们可就没力气活动啦。

简谐振动的能量要点简谐振动是物体在一些平衡位置附近以固定频率来回振动的运动方式。

它是一种理想化的振动模型，常用于描述弹簧和摆钟等物理系统的振动特性。

在简谐振动中，振动物体的能量一直保持着恒定。

以下是关于简谐振动能量的几个重要要点：1.势能和动能之间的转换：在简谐振动中，振动物体的能量主要由势能和动能组成。

当物体从平衡位置偏离时，会产生弹性势能。

随着物体向平衡位置回归，弹性势能转变为动能。

两种能量形式之间的转换是周期性的，能量在势能和动能之间交替转换，始终保持总能量不变。

2.势能的表达式：简谐振动的势能可以用一个二次函数来表达。

对于弹簧振子，势能与物体偏离平衡位置的平方成正比。

势能函数可以表示为U(x) = (1/2) kx²，其中k是弹簧劲度系数，x是物体离开平衡位置的位移量。

3.动能的表达式：振动物体的动能取决于物体的质量和速度。

动能可以表示为K = (1/2) mv²，其中m是物体的质量，v是物体的速度。

由于简谐振动中物体的运动速度是周期性变化的，动能的最大值等于势能的最大值。

4.总能量的守恒：在简谐振动中，总能量一直保持恒定。

振动物体的总能量可以表示为E=U+K，其中U是势能，K是动能。

由于振动物体在势能和动能之间交换能量，总能量以恒定的方式改变，但总能量的值始终保持不变。

5.振幅和能量关系：振动物体的振幅是指物体离开平衡位置的最大位移量。

振幅越大，物体在振动过程中的最大速度和最大加速度也会增大。

根据动能的表达式K = (1/2) mv²可以看出，振幅的增加会导致动能的增加，从而增加振动物体的总能量。

6.能量的周期性变化：简谐振动的能量以周期性的方式变化。

在振动周期的不同阶段，势能和动能的值会交替变化。

具体来说，在最大位移点，势能达到最大值而动能为零；在通过平衡位置时，势能为最小值而动能最大。

这种能量的周期性变化特性与简谐振动的周期性变化是紧密相关的。

简谐振动的能量与周期简谐振动是物体在弹性势能恢复力作用下进行的一种周期性振动。

在简谐振动中，能量与周期之间存在一定的关系。

下面将通过分析简谐振动的能量变化以及与周期之间的关系来探讨这一问题。

一、简谐振动的能量变化简谐振动的能量可以分为两部分，一部分是动能，另一部分是势能。

在振动过程中，物体在运动的过程中，动能和势能不断地相互转换，但其总和保持不变。

1. 动能的变化物体在振动过程中具有动能。

当物体达到最大振幅时，速度最大，此时动能也最大。

而当物体通过平衡位置时，速度为零，动能也为零。

因此，可以得出结论：动能随物体的位移而变化，与物体的位移成正比。

2. 势能的变化物体在振动过程中具有势能。

当物体位于极大位移时，弹性势能最大，此时势能也最大。

而当物体通过平衡位置时，位移为零，势能也为零。

因此，可以得出结论：势能随物体的位移而变化，与物体的位移成正比。

3. 能量守恒定律根据能量守恒定律，简谐振动中的能量保持不变。

即动能和势能之和等于常数。

可以用下式表示：E = K + U其中，E表示总能量，K表示动能，U表示势能。

因为动能和势能之和保持不变，所以在振动过程中，动能和势能的增减是互相抵消的。

二、简谐振动的周期与能量的关系简谐振动的周期是指完成一次完整振动所需要的时间。

简谐振动的周期与其能量之间存在一定的关系。

下面将从理论和实验两个方面探讨这一问题。

1. 理论推导简谐振动的周期与物体的振动频率有关。

振动频率可以用下式表示：f = 1 / T其中，f表示振动频率，T表示周期。

根据简谐振动的定义，可以得出如下的等式：ω^2 = k / m其中，ω表示角频率，k表示弹簧的劲度系数，m表示物体的质量。

角频率与振动频率之间存在如下的关系：ω = 2πf将振动频率表达式代入上式，可以得到：ω = 2π / T通过对上述等式的变换，可以得到简谐振动的周期与劲度系数和物体质量的关系：T = 2π√(m / k)由上式可以看出，简谐振动的周期与劲度系数和物体质量有关。