下载文档原格式
全国2008年4月自考信号与系统真题课程代码：02354一、单项选择题（本大题共12小题，每小题2分，共24分）在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1．RLC 串联电路发生谐振的条件是（ ）A ．LC10=ω B ．LC πω210=C ．LC f 10=D ．LCR=0ω2．已知信号)(t f 的波形如题2图所示,则)()1(t t f ε-的表达式为（ ）A ．)3(-t εB ．)3()(--t t εεC ．)(t εD ．)3()(+-t t εε 3．计算⎰∞∞-=-dt t t )6(sin 2πδ（ ） A ．1 B ．1/6C ．1/8D ．1/44．已知⎰∞-=t d t f ττδ)()(,则其频谱=)(ωj F （ ）A ．ωj 1B ．j ωC ．)(1ωπδω+j D ．)(1ωπδω+-j 5．信号)(1t f 与)(2t f 的波形分别如题5图(a ),(b )所示,则信号)(2t f 的频带宽度是信号)(1t f 的频带宽度的（ ）A ．2倍B ．1/2倍C ．1倍D ．4倍6．已知某周期电流t t t i 5sin 223sin 221)(++=,则该电流信号的有效值I 为（ ） A ．3A B ．1A C ．17A D ．10A 7．已知)(t f 的拉普拉斯变换为F (s ),⎰-∞-0)(dt t f 有界,则⎰∞-td f ττ)(的拉普拉斯变换为（ ）A ．)(1s F sB ．)0()(1--f s F sC ．⎰-∞-+0)(1)(1ττd f ss F sD ．⎰-∞--0)(1)(1ττd f s s F s8．已知)(t f 的拉普拉斯变换为F (s ),且F (0)=1,则⎰∞-0)(dt t f 为（ ）A ．π4B ．π2C ．π21D ．19．系统函数22)()(c a s bs s H +-+=,a ,b ,c 为实常数,则该系统稳定的条件是（ ）A ．a <0B ．a>0C ．a=0D ．c =010．已知某离散序列)(n f 如题10图所示,则该序列的数学表达式为（ ） A ．)1()1()(+-=n n f n ε B ．)1()1()(--=n n f n ε C ．)()1()(n n f n ε-=D ．n n f )1()(-=11．已知某系统的差分方程为)1()()2()1()(0101-+=-+-+n f b n f b n y a n y a n y ,则该系统的系统函数H (z )为（ ）A ．201011)(z a z a zb b z H +++= B ．211011)(1---+++=z a z a z b b z HC ．102120)(a z a z z b z b z H +++=D ．20111011)(---+++=z a z a z b b z H12．已知)1(3)(+=z zz F ,则)(n f 为（ ）A ．)()3(n n ε-B ．)()1(31n n ε-C ．)(31n nε⎪⎭⎫⎝⎛ D ．)(3n n ε二、填空题（本大题共12小题，每小题2分，共24分） 请在每小题的空格中填上正确答案。
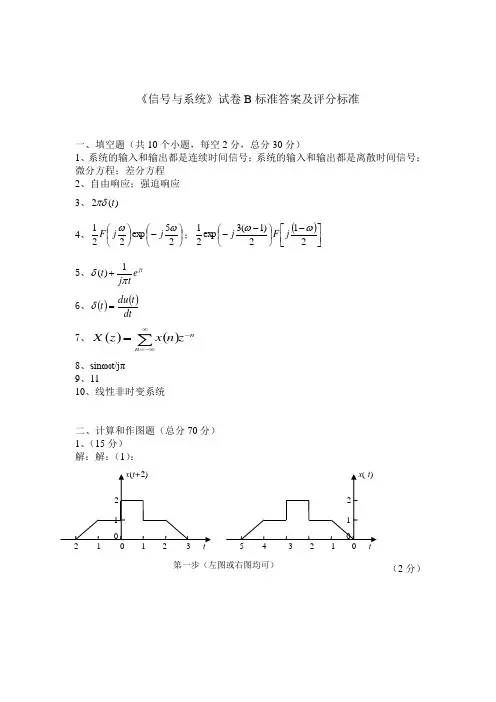
《信号与系统》试卷B 标准答案及评分标准一、填空题（共10个小题，每空2分，总分30分）1、系统的输入和输出都是连续时间信号；系统的输入和输出都是离散时间信号；微分方程；差分方程2、自由响应；强迫响应3、2()t πδ4、⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛25exp 221ωωj jF ；()⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛--212)1(3exp 21ωωj F j5、1()jtt e j tδπ+6、()()dtt du t =δ7、()()nn zn x z X -∞-∞=∑=8、sinω0t/jπ 9、1110、线性非时变系统二、计算和作图题（总分70分） 1、（15分） 解：解：（1）：（2分）第一步（左图或右图均可）（3分）（2）：（2分）（3分）（3）：第二步第一步，上面两种图形都可以第二步（5分）2. （15分）解：对1()f t 求导数得1'()f t ，对2()f t 求积分得(1)2()f t -，其波形如图1所示。
（4分）卷积(1)1212'()*()()*()f t f t f t f t -=，（3分）()()()()[]()()()[]()()()[]()()()()()()()()552444224112545242322112-----+-----=----+---------=t u t t u t t u t t u t t u t u t t u t u t t u t u t t f（5分）波形图如图2：（3分） 3、（15分）解：对方程两边取拉普拉斯变换，得2()(0)'(0)3()3(0)2()2()6()s Y s sy y sY s y Y s sF s F s --+-+=+2(32)()[(0)'(0)3(0)]2(3)()s s Y s sy y y s F s ++-++=+图1－2 2 图222(0)'(0)3(0)2(3)()()()()3232zi zs sy y y s Y s Y s Y s F s s s s s +++=+=+++++ （4分）又1()F s s=所以 22753()3212zi s Y s s s s s +==-++++22(3)1341()3212zs s Y s s s sss s +=⋅=-+++++ （4分）系统的零输入响应为：2()(53)()t t zi y t e e t ε--=- （2分） 零状态响应为：2()(34)()t t zs y t e e t ε--=-+ （2分） 全响应为：2()()()(32)()t t zi zs y t y t y t e e t ε--=+=+-。
杭州电子科技大学学生考试卷（ 期中）卷与解析考试课程 概率论与数理统计 考试日期2008年 11月 日 成 绩课程号 A0702140教师号任课教师姓名考生姓名参考答案 学号（8位）年级专业 一、选择题（每小题3分，共12分）1．设B A ,是两个互不相容的事件，0)(>B P ，则下列各式中一定成立的是（ C ） A ．1)(=B A P B ．)(1)(B P A P -= C ．0)(=B A P D ．0)(=AB P解析：知识点：1）若B A ,是两个互不相容的事件，则φ=AB ，可推0)(=AB P2）本题还用到条件概率公式)()()(B P AB P B A P =2．设随机事件B A ,满足)()(A B P B P =，则下列结论中正确的是 （ A ） A ．)()()(B P A P B A P = B ．)()()(B P A P B A P +=⋃ C ． B A ,互不相容 D ．)()(A B P A P =解析：由)()(A B P B P =得B A ,相互独立，则B A ，也相互独立。
而若B A ,是相互独立，则)()()(B P A P AB P =3． 随机变量X 的概率密度为),(,21)(4)3(2+∞-∞∈=+-x e x f x π，则=Y （ B ）)1,0(~N A ．23+X B ．23+XC ．23-X D ．23-X解析：正态分布的概率密度函数与参数μ和2σ的关系；及与标准正态分布的关系（转化）)1,0(~N X Y σμ-=4．设随机变量X 和Y 相互独立，其分布函数分别为)(x F X 与)(y F Y ，则随机变量 ),max(Y X Z =的分布函数)(z F Z 等于 （ C ） A ．)}(),(max{z F z F Y X B ．)]()([21z F z F Y X +C ．)()(z F z F Y X ⋅D ．)()()()(z F z F z F z F Y X Y X ⋅-+ 解析：1）二维随机变量函数的分布}),({}{)(z Y X G P z Z P z F Z ≤=≤=；2）若为二维离散型随机变量，则∑∑≤===≤=≤=zy x G j i Z j i y Y x XP z Y X G P z Z P z F ),(},{}),({}{)(；3）若为二维连续型随机变量，则⎰⎰≤=≤=≤=zy x G Z dxdy y x f z Y X G P z Z P z F ),(),(}),({}{)(。
学院 姓名 学号 任课老师 选课号……………密……………封……………线……………以……………内……………答……………题……………无……………效…………1、 两个联合平稳的随机过程为：()()()()00X cos Y sin t a t t b t ωω=+Θ=+Θ其中a 、b 、0ω皆为常数，Θ是在[]0,2π上均匀分布的随机变量。
试求互相关函数()()XY YX R R ττ和，并说明互相关函数在0τ=时的值具有什么意义。
（10分） 解：()()()()()()()()()()()()()0000000Y X 0c o s s i n s i n 22s i n 2sin 2sin 2XY XY R E X t Y t E a t b t abE t ababR R ττωωτωωωτωτωτττωτ=+⎡⎤⎣⎦⎡⎤=++Θ+Θ⎣⎦=++Θ-⎡⎤⎣⎦=--==()()YX 000XY R R ==，说明()()X t Y t 和在同一时刻正交，对于本题，()()0E X t E Y t =⎡⎤⎡⎤⎣⎦⎣⎦=，说明()()X t Y t 和在同一时刻还互不相关。
2、设有平稳过程()cos()X t a t =Ω+Θ，其中a 为常数，Θ是在[0,2]π上服从均匀分布的随机变量，Ω是概率密度函数满足()()f f ωω=-的随机变量，且Ω与Θ相互独立。
求证()X t 的功率谱密度2()()X S a f ωπω=。
（10分）解：[](,)cos()cos()X R t t E a t a t ττ+=Ω+Ω+ΘΩ+Θ[]2cos(22)cos()2a E t ττ=Ω+Ω+Θ+Ω 由于Ω与Θ相互独立[]2,()0cos(22)cos(22)(,)0E t t f d d πωτωωτθωθθωΩΦ∴Ω+Ω+Θ=++=⎰⎰[][]22(,)cos(22)cos()=cos()22X a a R t t E t E ττττ∴+=Ω+Ω+Θ+ΩΩ2cos()()2a f d ωτωω∞Ω-∞'''=⎰由于()()X X R S τω⇔，所以2()cos()()2X a S f d ωωτωω∞Ω-∞⎧⎫'''=⎨⎬⎩⎭⎰F2cos()()2j a f d e d ωτωτωωτ∞∞-Ω-∞-∞⎡⎤'''=⎢⎥⎣⎦⎰⎰ 2cos()()2j a e d f d ωτωττωω∞∞-Ω-∞-∞⎡⎤'''=⎢⎥⎣⎦⎰⎰()()2()2a f d πδωωδωωωω∞Ω-∞''''=-++⎡⎤⎣⎦⎰由于(), ()f δωωΩ''为偶函数，所以()()20()a f d πδωωδωωωω∞Ω''''=-++⎡⎤⎣⎦⎰()20()a f d πδωωωω∞Ω''=-⎰2()a f πωΩ=得证。
《数字信号处理》期末考试B卷答案一、单项选择题(本大题共10小题，每小题2分，共20分)在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.已知某序列z变换的收敛域为有限z平面，则该序列为( A )。
A.有限长序列B.右边序列C.左边序列D.双边序列2.下列系统(其中y(n)是输出序列，x(n)是输入序列)中______属于线性系统。
( C )A.y(n)=x2(n)B.y(n)=4x(n)+6C.y(n)=n2x(n-n0)D.y(n)=e x(n)3.下列关于因果稳定系统说法错误的是( A )A.极点可以在单位圆外B.系统函数的z变换收敛区间包括单位圆C.因果稳定系统的单位抽样响应为因果序列D.系统函数的z变换收敛区间包括z=∞4.按时间抽取的基-2FFT算法的运算量按频率抽取的基-2FFT算法。
( C )A.大于B.小于C.等于D.大小不确定5.序列x(n)=R7(n)，其16点DFT记为X(k)，k=0,1,…,15则X(0)为( D )。
A.2B.3C.4D.76.下面描述中最适合DFT的是（ B ）A．时域为离散序列，频域也为离散序列B．时域为离散有限长序列，频域也为离散有限长序列C．时域为离散无限长序列，频域为连续周期信号D．时域为离散周期序列，频域也为离散周期序列7.序列x1（n）的长度为4，序列x2（n）的长度为3，则它们线性卷积的长度是，5点圆周卷积的长度是。
（B）A. 5, 5B. 6, 5C. 6, 6D. 7, 58.无限长单位冲激响应（IIR）滤波器的结构是______型的( C )A. 非递归B. 反馈C. 递归D. 不确定9．利用矩形窗函数法设计FIR滤波器时，在理想特性的不连续点附近形成的过滤带的宽度近似等于( A )。
A.窗函数幅度函数的主瓣宽度B.窗函数幅度函数的主瓣宽度的一半C.窗函数幅度函数的第一个旁瓣宽度D.窗函数幅度函数的第一个旁瓣宽度的一半 10.下列系统哪个属于全通系统（ A ）。
学院 姓名 学号 任课老师 选课号……………密……………封……………线……………以……………内……………答……………题……………无……………效…………1. （10分）随机变量12,X X 彼此独立，且特征函数分别为12(),()v v φφ，求下列随机变量的特征函数： （1）122X X X =+ （2）12536X X X =++解：（1）()121222()jv X X jvX jv X jvXX v E e E e E e e φ+⎡⎤⎡⎤⎡⎤===⋅⎣⎦⎣⎦⎣⎦1221212()(2)jvX jv X X X E e E e v v φφ⎡⎤⎡⎤=⎣⎦⎣⎦和独立（2）()1212536536()jv X X jv X jv X jv X v E e E e e e φ++⎡⎤⎡⎤==⋅⋅⎣⎦⎣⎦1253612jv X jv X jv X X E e E e E e ⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦和独立 612(5)(3)jv e v v φφ=2. （10分）取值()1,1-+，概率[0.4,0.6]的独立()半随机二进制传输信号()X t ，时隙长度为T ，问： （1） 信号的均值函数()E X t ⎡⎤⎣⎦； （2） 信号的自相关函数(),X R t t τ+； （3） 信号的一维概率密度函数();X f x t 。
解：（1）()10.410.60.2X t E =-⨯+⨯=⎡⎤⎣⎦(2) 当,t t τ+在同一个时隙时：[]222(,)()()[()]10.6(1)0.41X R t t E X t X t E X t ττ+=+==⨯+-⨯=当,t t τ+不在同一个时隙时：[][][](,)()()()()0.20.20.04X R t t E X t X t E X t E X t τττ+=+=+=⨯=（3）()()();0.610.41X f x t x x δδ=-++3. （10分）随机信号0()sin()X t t ω=+Θ，()()0cos Y t t ω=+Θ，其中0ω为常数，Θ为在[]-,ππ上均匀分布的随机变量。
全国2008年4月自考信号与系统真题课程代码：02354一、单项选择题（本大题共12小题，每小题2分，共24分）在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1．RLC 串联电路发生谐振的条件是（ ）A ．LC 10=ωB ．LC πω210=C ．LC f 10=D ．LCR=0ω2．已知信号)(t f 的波形如题2图所示,则)()1(t t f ε-的表达式为（ ）A ．)3(-t εB ．)3()(--t t εεC ．)(t εD ．)3()(+-t t εε 3．计算⎰∞∞-=-dt t t )6(sin 2πδ（ ） A ．1 B ．1/6C ．1/8D ．1/44．已知⎰∞-=t d t f ττδ)()(,则其频谱=)(ωj F （ ）A ．ωj 1 B ．j ω C ．)(1ωπδω+j D ．)(1ωπδω+-j5．信号)(1t f 与)(2t f 的波形分别如题5图(a ),(b )所示,则信号)(2t f 的频带宽度是信号)(1t f 的频带宽度的（ ）A ．2倍B ．1/2倍C ．1倍D ．4倍6．已知某周期电流t t t i 5sin 223sin 221)(++=,则该电流信号的有效值I 为（ ） A ．3A B ．1A C ．17A D ．10A 7．已知)(t f 的拉普拉斯变换为F (s ),⎰-∞-0)(dt t f 有界,则⎰∞-td f ττ)(的拉普拉斯变换为（ ）A ．)(1s F sB ．)0()(1--f s F sC ．⎰-∞-+0)(1)(1ττd f ss F sD ．⎰-∞--0)(1)(1ττd f s s F s8．已知)(t f 的拉普拉斯变换为F (s ),且F (0)=1,则⎰∞-0)(dt t f 为（ ）A ．π4B ．π2C ．π21D ．19．系统函数22)()(c a s bs s H +-+=,a ,b ,c 为实常数,则该系统稳定的条件是（ ）A ．a <0B ．a>0C ．a=0D ．c =010．已知某离散序列)(n f 如题10图所示,则该序列的数学表达式为（ ）A ．)1()1()(+-=n n f n εB ．)1()1()(--=n n f n εC ．)()1()(n n f n ε-=D ．n n f )1()(-=11．已知某系统的差分方程为)1()()2()1()(0101-+=-+-+n f b n f b n y a n y a n y ,则该系统的系统函数H (z )为（ ）A ．201011)(z a z a zb b z H +++= B ．211011)(1---+++=z a z a z b b z HC ．102120)(a z a z z b z b z H +++=D ．20111011)(---+++=z a z a z b b z H12．已知)1(3)(+=z zz F ,则)(n f 为（ ）A ．)()3(n n ε-B ．)()1(31n n ε-C ．)(31n nε⎪⎭⎫⎝⎛ D ．)(3n n ε二、填空题（本大题共12小题，每小题2分，共24分） 请在每小题的空格中填上正确答案。
电⼦科技⼤学随机信号分析中期考题2006随机（A）1.设随机过程21)(cos )(2-Θ+=t t X ω，Θ是随机变量，其特征函数为)(υφΘ。
证明：)(t X 是⼴义平稳随机过程的充要条件是0)4()2(==ΘΘφφ。
证明：（1）)(t X 的均值为：()21()[()][cos ()]2111[1cos 2()][cos(22)]22211cos(2)[cos(2)]sin(2)[sin(2)]22X m t E X t E t E t E t t E t E ωωωωω==+Θ-=++Θ-=+Θ=Θ-Θ由上式可知，当且仅当0)]2sin()2[cos(][)2(2=Θ+Θ==ΘΘj E e E j φ时，()0X m t =，才与t ⽆关。
（2）)(t X 的相关函数为：22(,)[()()]11[(cos ())(cos ())]2211[cos(222)cos(22)]22[cos(2)][cos(424)]811cos(2)cos(42)[cos(4)]881sin(42)][sin(4)]8X R t t E X t X t E t t E t t E E t t E t E ττωωτωωωτωωτωωτωτωωτωωτ+=+=++Θ-+Θ-=++Θ?+Θ+++Θ==++Θ-+Θ同理可得，当且仅当0)]4sin()4[cos(][)4(4=Θ+Θ==ΘΘj E eE j φ时，)cos(21),(ωττ=+t t R X 与t ⽆关。
2.设随机过程)sin()(0Θ+Ω=t A t X ，其中0A 为常数，ΘΩ和为相互独⽴的随机变量，Ω在]2010[ππ内均匀分布，Θ在]20[π内均匀分布。
证明：（1） )(t X 是⼴义平稳随机信号；（2） )(t X 的均值是各态历经的。
解：（1）00000[()][sin()][sin()cos()cos()sin())][sin()][cos()][cos()][sin())]0E X t E A t E A t A t A E t E A E t E =Ω+Θ=ΩΘ+ΩΘ=ΩΘ+ΩΘ= 202020(,)[()()][sin()sin()]cos()cos(22)2cos()2X R t t E X t X t A E t t t A E A E ττττττ+=+=Ω+Ω+ΘΩ+ΘΩ-Ω+Ω+Θ??=Ω??=所以)(t X 是⼴义平稳随机信号（2）[]00000001[()][sin()]lim sin()lim sin()lim cos()|0TT T T T T A X t A A t A t dtT A A t d t t T T →+∞→+∞→+∞=Ω+Θ=Ω+Θ=Ω+ΘΩ=-Ω+Θ=ΩΩ时间平均等于统计平均，所以)(t X 的均值是各态历经的。
