MFSK的调制与解调
- 格式:docx
- 大小:235.61 KB
- 文档页数:14


多进制数字相位调制(MPSK)1前言:VHDL主要用于描述数字系统的结构,行为,功能和接口。
除了含有许多具有硬件特征的语句外,VHDL的语言形式和描述风格与句法是十分类似于一般的计算机高级语言。
VHDL的程序结构特点是将一项工程设计,或称设计实体(可以是一个元件,一个电路模块或一个系统)分成外部(或称可是部分,及端口)和内部(或称不可视部分),既涉及实体的内部功能和算法完成部分。
在对一个设计实体定义了外部界面后,一旦其内部开发完成后,其他的设计就可以直接调用这个实体。
这种将设计实体分成内外部分的概念是VHDL系统设计的基本点。
2设计主题2.1设计目的(1).掌握MPSK的设计原理(2).掌握MPSK的VHDL设计2.2 MPSK的设计原理多进制数字相位调制也称多元调相或多相制。
它利用具有多个相位状态的正弦波来代表多组二进制信息码元,即用载波的一个相位对应于一组二进制信息码元。
如果载波有2k 个相位,它可以代表 k位二进制码元的不同码组。
多进制相移键控也分为多进制绝对相移键控和多进制相对(差分)相移键控。
下面以四相相位调制为例进行讨论。
四相调相信号是一种四状态符号,即符号有00、01、10、11四种状态。
所以,对于输入的二进制序列,首先必须分组,每两位码元一组。
然后根据组合情况,用载波的四种相位表征它们。
这种由两个码元构成一种状态的符号码元称为双比特码元。
同理,k位二进制码构成一种状态符号的码元则称为k比特码元、四相PSK(4PSK)信号实际是两路正交双边带信号。
串行输入的二进制码,两位分成一组。
若前一位用A表示,后一位用B表示,经串/并变换后变成宽度加倍的并行码(A、B码元在时间上是对齐的)。
再分别进行极性变换,把单极性码变成双极性码,然后与载波相乘,形成正交的双边带信号,加法器输出形成4PSK信号。
显然,此系统产生的是π/4系统PSK信号。
如果产生π/2系统的PSK信号,只需把载波移相π/4后再加到乘法器上即可。

基于FPGA的MFSK调制解调器设计与实现FPGA技术(Field Programmable Gate Array)是一种可编程逻辑器件,广泛应用于数字电路的设计和实现。
在通信领域,FPGA可以用于实现各种数字调制解调器。
本文将介绍基于FPGA的MFSK(多频移键控)调制解调器的设计与实现。
第一部分:引言MFSK调制是一种多音调调制技术,常用于数字通信系统中。
它利用多个不同频率的正弦波信号来表示数字信息。
MFSK调制可以提供更高的抗干扰性能和更高的传输效率,因此在许多应用场景下得到广泛应用。
本文将利用FPGA技术设计一个MFSK调制解调器,并通过实现一个实例来验证其性能。
第二部分:MFSK调制解调器的原理MFSK调制解调器的主要任务是将数字信息转换为MFSK信号进行传输,并将接收到的MFSK信号解调还原为数字信息。
MFSK调制的原理是将数字信息编码为不同频率的正弦波信号,然后进行叠加。
解调时,通过对接收到的信号进行频率分析,可以恢复出原始的数字信息。
第三部分:FPGA的设计与实现在FPGA中实现MFSK调制解调器需要考虑到以下几个关键模块:1. 时钟模块:利用FPGA提供的时钟资源生成所需的时钟信号,用于同步调制解调器的各个模块。
2. 数字信息编码模块:将输入的数字信息转换为相应的MFSK信号,生成给调制模块使用。
3. 调制模块:将生成的MFSK信号与载波信号相乘,得到最终的调制信号。
4. 接收模块:接收到的MFSK信号与本地生成的载波信号相乘,然后通过低通滤波器进行滤波,得到解调后的信号。
5. 数字信息解码模块:对解调后的信号进行频率分析,将其转换为对应的数字信息。
第四部分:实例演示以一个4FSK调制解调器为例,假设输入的数字信息为"1010"。
首先,在数字信息编码模块中将其转换为相应的4FSK信号,如频率分别为f1、f2、f3、f4的四个正弦波信号。
然后,在调制模块中将生成的4FSK信号与本地生成的载波信号相乘得到调制后的信号。


mfsk调制解调
MFSK调制解调是指多频移键控(MFSK)调制解调技术。
它是一种高效的数字通信技术,在无线电广播、电视广播和无线电通信等领域都有广泛的应用。
MFSK调制是将数字信号转换为模拟信号的过程,通过将数字数据分成几个独立的频率信号,并将它们叠加在一起来实现。
每个频率信号代表一个特定的数字。
例如,对于4FSK(四频移键控)调制,可以使用四个不同的频率信号来表示四个不同的数字。
MFSK调制可以使用不同的调制方案,如二进制相移键控(BPSK)和四进制相移键控(QPSK)等。
MFSK解调是将模拟信号转换回数字信号的过程,通过检测接收信号的频率成分并将其与预定义的频率进行比较来实现。
根据最接近的频率,接收器可以确定接收到的数字信号是什么。
解调器还需要处理噪声和干扰,以确保接收到的数字信号的准确性。
在MFSK系统中,发送端将输入的二进制码元经过逻辑电路和串/并变换电路转换为M进制码元,每k位二进制码分为一组,用来选择不同的发送频率。
在接收端,当某一载波频率到来时,只有相应频率的带通滤波器能收到信号,其它带通滤波器输出的都是噪声。
抽样判决器的任务就是在某一时刻比较所有包络检波器的输出电压,通过选择最大值来进行判决。
将最大值输出就得到一个M进制码元,然后,再经过逻辑电路转换成k位二进制并行码,再经过并/串变换电路转换成串行二进制码,从而完成解调过程。
MFSK调制解调技术具有高频谱效率、良好的抗干扰性能和简单
的实现等优势,因此在无线电通信领域得到广泛应用。

多进制频率调制解调系统的设计XX(XX理工学院电信工程系电子信息工程专业,2007级6班,XXXX XX)指导老师:XX[摘要]MFSK ---多进制数字频率调制,简称多频制,是2FSK方式的推广。
它是用不同的载波频率代表各种数字信息。
在数字通信系统中,数字调制与解调技术占有非常重要的地位。
随着FPGA 技术的发展,数字通信技术与 FPGA的结合体现了现代数字通信系统发展的一个趋势。
文中介绍了MFSK 调制解调的原理, 并基于 VHDL 实现了MFSK 调制解调电路设计,仿真结果表明设计方案是可行的。
整个系统的功能在EDA技术开发平台均调试通过,并在MAX7000S系列FPGA上硬件实现,具有较高的实用性和可靠性。
[关键词]MFSK;VHDL;调制;解调Design and Simulation of MFSK ModulationCircuit Based on VHDLXX(Grade 03,Class 1,Major electronics and information engineering ,Electronics and information engineering Dept.,XX University of technology XXXX,XX)Tutor: XX[Abstract]MFSK --- Multi-band digital frequency modulation, referred to as multi-frequency system is the way 2FSK promotion. It is representative of a different variety of digital information carrier frequency. In digital communication system, the digital modulation and demodulation plays an important role with the development of FPGA technology, the combination of digital communication technology with FPGA is an inevitable trend. This paper gives the principle of MFSK modulation and demodulation. Based on VHDL,the design of MFSK modulation circuit is realized. The simulation result indicates that this scheme is feasible.[Key words]MFSK;VHDL; modulation; demodulation目录1绪论11.1MAXPLUXII简介31.2VHDL语言简介41.3多进制调制的特点52方案论证82.1FPGA简介82.2FPGA概述82.3ALTERA可编程逻辑器件简介93多进制数字调制原理103.1FSK调制解调的基本原理103.2MFSK简介123.3多进制数字频率调制的原理123.4多进制数字频率解调的原理133.5MFSK调制解调原理143.6MFSK信号的频谱、带宽与频带利用率153.7MFSK系统的误码性能164 MFSK的VHDL 建模与设计164.1MFSK调制电路的VHDL建模与设计与实现164.2MFSK解调电路的VHDL建模与设计与实现174.3MFSK调制解调电路的VHDL建模与设计与实现19 5硬件实现215.1程序下载215.2波形验证225.3结果分析与体会23结论24致25参考文献26附录A英文文献:27中文翻译:31附录B原文总程序:341绪论如今社会通信技术的发展速度可谓日新月异,计算机的出现在现代通信技术的各种媒体中占有独特的地位,计算机在当今社会的众多领域里不仅为各种信息处理设备被使用,而且它与通信向结合,使电信业务更加丰富。




利用随机共振解调微弱MFSK信号
利用随机共振解调微弱MFSK信号
在通信领域,MFSK (多频移键)是一种用广泛的频率调制技术,它可以在不同的载波频率上传输多个信息比特。
然而,由于MFSK信号本身很微弱,因此在传输过程中容易遭受干扰和噪声的影响,从而导致信号接收质量的降低。
为了解决这个问题,科学家们提出了一种新的解调方法:随机共振解调。
随机共振解调是一种先进的探测技术,它利用噪声和随机电路来增强微弱信号的强度,并提高信噪比,从而实现MFSK信
号的有效解调。
具体过程如下:
首先,将接收到的MFSK信号输入到随机共振电路中处理。
随机共振电路中包括一个噪声源和一个随机振荡器,当这两个元件相互作用时,会产生一种特殊的随机共振现象,使得电路的输出信号与输入信号之间产生频率差异,从而在保持相位不变的情况下,增强了输入信号的强度。
然后,在信号经过随机共振电路处理后,使用相干解调器将信号解调。
这时,由于随机共振电路的作用,信号已经变得强大,并且将接收到的噪声信号与随机电路中产生的噪声信号进行相消,进一步提高了信噪比。
最后,将解调后的信号送入MFSK解码器进行解码处理即可。
利用随机共振解调微弱MFSK信号有很多优点。
首先,随机
共振电路可以增强微弱信号的强度,并提高信噪比;其次,在保持相位不变的情况下,可以实现对信号的高效解调;最后,随机共振解调对线路要求较低,适用于不同环境下的通信。
总之,随机共振解调是一种新兴的解调技术,它可以有效地提高微弱MFSK信号的接收质量,实现高效通信。
在未来的通信领域中,随机共振解调技术将成为一种重要的发展方向。
doi:10.3969/j.issn.1003-3114.2022.03.024引用格式:李濛,吴呈瑜,占敖.基于正交MFSK信号的解调优化算法[J].无线电通信技术,2022,48(3):541-546.[LIMeng,WUChengyu,ZHANAo.OptimizationAnalysisofDemodulationBasedonQuadratureMFSKSignal[J].RadioCommunica⁃tionsTechnology,2022,48(3):541-546.]基于正交MFSK信号的解调优化算法李㊀濛,吴呈瑜∗,占㊀敖(浙江理工大学信息学院,杭州浙江310018)摘㊀要:针对传统多进制频移信号解调算法存在计算量大㊁误码率高等问题,提出了一种基于正交多进制频移键控(MultipleFrequencyShiftKeying,MFSK)信号的解调算法㊂该算法通过检测和判决MFSK信号在不同频率点处的功率谱峰值来完成信号同步,然后对信号的同向分量和正交分量进行反正切运算求得信号斜率,再根据信号斜率构建差值序列并建立MFSK信号解调数学模型,最后通过模型求解完成信号的调制进制识别和解调㊂该算法复杂度较低且仅呈线性增长,仿真结果表明该算法在性能上优于传统的小波解调算法,且当输入信噪比大于6dB时,对2FSK㊁4FSK㊁8FSK和16FSK的解调正确率都可以达到90%以上㊂关键词:MFSK;信号解调;误码性能;位同步中图分类号:TP92㊀㊀㊀文献标志码:A㊀㊀㊀开放科学(资源服务)标识码(OSID):文章编号:1003-3114(2022)03-0541-06OptimizationAnalysisofDemodulationBasedonQuadratureMFSKSignalLIMeng,WUChengyu∗,ZHANAo(SchoolofInformationandTechnology,ZhejiangSci⁃TechUniversity,Hangzhou310018,China)Abstract:Aimingattheproblemsofhighcomputationalcomplexityandhighbiterrorrateintraditionalmulti⁃systemfrequency⁃shiftedsignaldemodulationalgorithm,ademodulationalgorithmbasedonquadratureMFSK(MultipleFrequencyShiftKeying)signalisproposed.ThealgorithmcompletessignalsynchronizationbydetectingandjudgingpowerspectrumpeaksoftheMFSKsignalatdifferentfrequencypoints,andthenperformsarctangentoperationonthein⁃directionandquadraturecomponentsofthesignaltoobtainsignalslope,constructsthedifferencesequenceaccordingtothesignalslope.NextitestablishthemathematicalmodelofMFSKsignaldemodu⁃lation,andfinallycompletesignalmodulationsystemidentificationanddemodulationthroughmodelsolution.Thecomplexityofthealgo⁃rithmislowandonlyincreaseslinearly.Simulationresultsshowthatthealgorithmissuperiortothetraditionalwaveletdemodulational⁃gorithminperformance,andwhentheinputsignal⁃to⁃noiseratioisgreaterthan6dB,thedemodulationaccuracyof2FSK,4FSK,8FSKand16FSKcanreachmorethan90%.Keywords:MFSK;signaldemodulation;biterrorperformance;bitsynchronization收稿日期:2022-03-15基金项目:国家自然科学基金(61801430);浙江理工大学基本科研业务费专项资金资助(2021Q029)FoundationItem:NationalNaturalScienceFoundationofChina(61801430);FundamentalResearchFundsofZhejiangSci-TechUniversity(2021Q029)0 引言频移键控信号(FrequencyShiftKeying,FSK)[1]具有产生方法简单㊁易于实现㊁可以异步传输和抗噪声能力强的性能,使得多进制频移键控(MultipleFrequencyShiftKeying,MFSK)信号在无线通信中得到广泛的应用[2]㊂目前对MFSK信号的解调方法主要包括快速傅里叶变换(FastFourierTransform,FFT)[3]㊁短时傅里叶变化(Short⁃TimeFourierTransform,STFT)[4]以及小波变化[5]解调算法㊂文献[6]中FFT解调器方案是根据同相(I)和正交(Q)样本组成的接收信号输入FFT后,通过选取FFT输出中可选功率最大的位置,对信号进行解调,但该方法的复杂度较高,信号处理效率较低㊂文献[7]中基于STFT是通过求解信号的能量系数,根据其序列的极大值点对应着时频能量来对信号进行解调,但抗噪性能较差且只对低阶的MFSK信号效果较好㊂文献[8]基于小波变化对信号进行解调是通过对小波脊线提取进而得到信号的瞬时频率,但小波变化存在小波尺度盲点㊁抗噪声性能差等问题㊂文献[9]中MFSK正交解调方案通过对瞬时速率的抽样判决完成对信号的解调,但没有对高噪声的信号进行进一步处理,抗噪能力较弱㊂近几年有采用神经网络[10-14]对信号进行解调,效果较好,但该方法需要大量数据,且仅针对特定训练的信号效果较好㊂本文通过MFSK信号I㊁Q两路的正交特性和频域特性对信号的信号同步㊁调制码识别和进制识别进行了研究:通过对信号不同频率点处的功率谱峰值进行检测判决完成了信号同步;通过信号的正交特性进而对信号斜率进行提取,再根据信号斜率构建差值序列并建立解调的数学模型,完成了调制进制M的识别和调制码的解调㊂本文的算法复杂度较低且仅呈线性增长,有着较高的信号处理速率和较广应用前景㊂1㊀系统模型MFSK是一种可用多个不同的载波频率代表多种数字信息的调制方式[15],其表达式为:S(n)=ð+ɕm=-ɕA0g(n-m)cos((ωc+amΔω)n),(1)式中,A0为信号幅度,g(n-m)表示基带信号,amɪ{1,2,3, ,M}为发送的数据,Δω为载波频率间隔㊂通过将接收的MFSK信号相干解调处理后,可以得到两路正交的I㊁Q信号,如式(2)所示:SI(n)=ð+ɕm=-ɕA0g(n-m)cos(amΔωn)SQ(n)=ð+ɕm=-ɕA0g(n-m)sin(amΔωn)ìîíïïïï㊂(2)根据式(2)中的SI(n)和SQ(n),进一步建立优化模型求解信号所有码元数的实际信号和设定信号之间的最小频率误差,设定H为频率误差,以信号频率的取值范围为约束条件,则该优化模型可表示为:minak,tH=ðLk=1A0cos(akω)-SQ(t+(k-1)N:t+k㊃N)+A0sin(akω)-SI(t+(k-1)N:t+k㊃N)s.t.a1<ak<am,(3)式中,L为信号的总码元数,ak为信号第k个码元所发送的数据,SQ和SI为信号的同向和正交分量,t为信号的起始点,N为信号的码元长度㊂上述问题是一个含离散变量的非凸非线性规划问题,难以获得其最优解[16],在实际问题中,信号长度往往很长,调制进制也会出现16㊁32等较高的阶的情况,会进一步增加问题求解的复杂度㊂本文通过对上述问题进行简化,求解该问题的次优解,进而减少计算的复杂度和计算量㊂2㊀MFSK信号解调模型本文首先计算信号起始点位置,再根据信号的正交性对式(3)中的优化问题进行简化并求其次优解,具体如下:①信号同步:首先将MFSK信号通过FFT变化进行信号同步,找到信号的起始点t㊂②信号解调:通过I㊁Q两路信号的相位正交性得到信号的斜率,根据信号斜率构建差值序列对信号进行建模解调,求解出该问题的次优解㊂2.1㊀信号同步假设接收到信号的采样率为FS,码速率为C,此时码元长度N=Fs/C,通过FSK信号和FFT的原理可知,通过对长度为N的信号进行FFT,可以得到当前码元的频率值㊂并根据得到频率值进行判决可以完成信号同步,以下是进行信号同步的步骤,假设数据的起始位置计为t:①读取t到t+N的数据,进行FFT;②计算出所得功率谱中最大值max(A)及最小值min(A),并设定需要进行判决的门限D=max(A)/min(A);③当得到的门限D小于一个设定值,并且此时的最大值max(A)大于一个设定的门限,将其判定为有效信息;④找到当前频率谱中最大的两个值,t值递增,当频率谱中这两个值最接近时,此时t处于符号的中间位置,在向前移动半个码元,即可得到信号的起始位置㊂2.2㊀信号解调首先将MFSK信号的I㊁Q两路信号SI㊁SQ进行反正切运算得到信号的斜率Sv:Sv=arctanSISQæèçöø÷,(4)Sv(x)=arctansin(pωx)cos(pωx)[],pɪ{a1,a2,a3, ,aM},(5)Sv(x)=pωx,xɪ(-kπ/2,kπ/2),k=1,2,3 ,n,(6)其中,pɪ{a1,a2,a3, ,aM}为发送的数据㊂考虑到实际系统中反正切运算量较大,且在FPGA中也难以直接实现,通过式(7)改进算法来简化计算过程[9]:Sᶄv(x)=SQ(x-1)SI(x)-SQ(x)SI(x-1)SI2(x)+SQ2(x)㊂(7)通过式(6)可以看出不同频率的信号对应不同的斜率,通过对相邻的两斜率值求差,可得不同频率信号的斜率差值d(k):d(k)=Sv(π2)-Sv(-π2)[]π=pω=akωkɪ{1,2,3, ,M}㊂(8)由于不同频率的信号对应不同的斜率,可以通过斜率差值的数量确定MFSK信号的调制进制M㊂将得到的M个差值通过式(8)构建差值序列R1 RM,再将信号的斜率Sv通过式(9)进行求差,得到整段信号的斜率差值Sc,并对Sc进行低通滤波以减少高频噪声的影响,最后建立以频率误差H最小化为目标,以差值序列的取值范围为约束的优化模型㊂Rk=d(k)㊃IN,1,(9)Sc=Sv(n+1)-Sv(n),(10)㊀minRkiH=ðLi=1|Rki-Sc(t+(i-1)N:t+i㊃N)|s.t.Rkiɪ{R1,R2,R3, ,RM},(11)其中,IN,1是长度为码元长度N的单位矩阵,Sc(t+(i-1)㊃N:t+i㊃N)为信号的第i个码元㊂对于上述优化问题,根据式(8)所得斜率差值,设定不同的门限值,进行门限判决进而求解出每个码元的频点㊂对信号一个长度为N的码元进行求解的时间复杂度为O(N),对L个码元的信号建立模型求解的总计时间复杂度为O(LN),算法复杂度仅呈线性增长㊂通过解决式(9)的问题,可确定Sv中每段信号所处的频点,最后再根据MFSK调制映射对照关系解出比特信息㊂2.3㊀算法的实现首先设定W初始值为0,截取W W+N信号进行FFT,当功率谱中最大值和最小值的比值不符合判决门限时,W不断递增,直到功率谱中最大的两个值之差最小时,可得信号的起始点为W-N/2,再通过反正切运算得到信号的斜率,并构建差值序列对信号进行建模解调,算法实现的具体流程如图1所示㊂图1㊀算法实现程序流程框图Fig.1㊀Algorithmimplementationprogramflowdiagram㊀㊀算法实现的伪代码如算法1所示,首先将FFT变化后信号中的最大值result和次大值result1提取出来,并设定判决门限set1和set2,当满足判决门限时且result与result1差值最小时,得到信号起始点为W-N/2,再通过反正切运算得到信号斜率Sv,并求得信号的斜率差值d(k),最后根据斜率差值,设定不同的门限值,进行门限判决进而求解出每个码元的频点㊂算法1解调算法输入:接收信号S,I路信号SI,Q路信号SQ,码元长度N输出:Rn码元频点1:functionDemodulation(S,SI,SQ,N)2:㊀㊀Wѳ03:㊀㊀while1do4:㊀㊀WѳW+15:㊀㊀cѳmin(result)/106:㊀㊀resultѳFFT(S/(W+(k-1)N:W+Nˑk),N)7:㊀㊀result1ѳresult[find(result=max(result))]=null8:㊀㊀set1ѳ4ˑmean(result)/min(result)9:㊀㊀set2ѳ5ˑmean(result)10:㊀Dѳmax(result)/min(result)11:㊀ifD<set1andmax(result)>set2then12:㊀㊀ifmax(result)-max(result)<cthen13:㊀㊀㊀tѳW-N/214:㊀㊀㊀Break15:㊀㊀endif16:㊀endif17:㊀mѳ018:㊀Rѳ019:㊀Lѳlength(S)/N20:㊀Svѳarctan(SI/SQ)21:㊀fork=0ңlength(Sv)-1do22:㊀㊀d(k)ѳSv(k+1)-Sv(k)23:㊀endfor24:㊀fori=1ңLdo25:㊀㊀ifRʂ(ðt+Nˑik=t+Nˑ(i-1)d(k)/N)then26:㊀㊀mѳm+127:㊀㊀R(m)ѳ(ðt+Nˑik=t+Nˑ(i-1)d(k)/N28:㊀㊀endif29:㊀endfor30:㊀fori=1ңLdo31:㊀㊀fork=1ңmdo32:㊀㊀㊀H(k)ѳR(k)-d(t+Nˑ(i-1),t+Nˑi)33:㊀㊀endfor34:㊀Rn(i)ѳmin(H)35:㊀endfor36:㊀returnRn3 仿真实验及结果分析为比较本文算法以及文献[17]的算法,设置仿真参数如表1所示㊂表1㊀仿真参数设置Tab.1㊀Simulationparametersettings仿真参数参数值采样率512kHz码元长度1000基频10kHz载频间隔10kHz同时设置实验如下:通过Matlab仿真生成2FSK㊁4FSK㊁8FSK㊁16FSK信号,信号的先验信息保持一致,均采用加性的高斯白噪声,信噪比为1dB步进到12dB,每个不同信噪比下均进行200次蒙特卡罗试验,分别使用文献[17]算法㊁传统相干解调[18]和本文算法进行计算㊂仿真不同进制下的解调误码率,三种算法的误码率曲线如图2 图5所示㊂图2㊀2FSK性能对比Fig.2㊀2FSKperformancecomparison图3㊀4FSK性能对比Fig.3㊀4FSKperformancecomparison图4㊀8FSK性能对比Fig.4㊀8FSKperformancecomparison图5㊀16FSK性能对比Fig.5㊀16FSKperformancecomparison由图2 图5可以看出,本文算法在实验过程中有良好的稳定性和准确性㊂在低信噪比(<6dB)时,斜率差值误差较大,导致无法正确地设置判决门限,误码率较高;在高信噪比(>6dB)时,2FSK㊁4FSK㊁8FSK和16FSK的解调正确率都可以达到90%以上,且表现出很高的稳定性,解调性能优于传统的小波解调和相干解调算法㊂当面对一个未知的信号时,基于小波变化的解调算法无法事先确定好尺度因子的选择㊂因此,可以认为本文算法所需先验知识更少,本文算法也更加适用于MFSK信号的解调[19]㊂4 结束语本文提出了一种基于正交MFSK信号的解调算法,首先利用MFSK信号在功率谱中的能量聚集性,对功率谱频率的峰值进行检测判决来完成信号同步,然后利用信号的正交性对信号斜率进行提取,最后根据信号斜率构建差值序列并建立解调的数学模型,完成了调制进制M的识别和调制码的解调㊂本文算法复杂度较低且仅呈线性增长,仿真结果表明,有较为理想的处理性能和较高的运行效率,适于工程实现㊂参考文献[1]㊀BARISB,CEKME,KUNTALPDG.ModulationClassifi⁃cationofMFSKModulatedSignalsUsingSpectralCentroid[J].WirelessPersonalCommunications,2021,119:763-775.[2]㊀徐建飞,汪芙平,王赞基.基于全数字锁相环的MFSK信号盲解调算法[J].计算机应用研究,2011,28(10):3852-3854.[3]㊀杨丽娟,张白桦,叶旭桢.快速傅里叶变换FFT及其应用[J].光电工程,2004(S1):1-3,7.[4]㊀PRǓŠAZ,BALAZSP,SØNDERGAARDPL.ANonitera⁃tiveMethodforReconstructionofPhasefromSTFTMag⁃nitude[J].IEEE/ACMTransactionsonAudio,Speech,andLanguageProcessing,2017,25(5):1154-1164.[5]㊀陈锦,罗晓曙.一种新的基于小波变换的QPSK信号解调方法[J].广西师范大学学报(自然科学版),2016,34(2):35-45.[6]㊀MOONS,KIMS,JEUNGS,etal.ExactClosed⁃formPerformanceAnalysisofMFSKDemodulatorBasedonFFT[C]ʊTENCON2005-2005IEEERegion10Confer⁃ence.Melbourne:IEEE,2005:1-4.[7]㊀李伟,谢华.短时傅里叶变换在频移键控解调中的应用[J].电子测量技术,2011,34(7):34-36,42.[8]㊀林财永,张国毅,李英达,等.基于循环谱和小波变换的MFSK信号解调算法[J].科学技术与工程,2013,13(28):8293-8298.[9]㊀钱者凤.MFSK信号新型正交解调算法[J].电子设计工程,2018,26(21):106-109,114.[10]LIUCY,ROMERORA.DeepNeuralNetworkDetectionforPulsedRadar⁃EmbeddedM⁃PSKCommunications[C]ʊ202017thEuropeanRadarConference(EuRAD).Utrecht:IEEE,2021:238-241.[11]TANQ,ZHAOL.MSKDemodulatorandImpulsiveNoiseDepressionBasedonConvolutionalNeuralNetworkwithGatedLayers[C]ʊ2019IEEE5thInternationalConferenceonComputerandCommunications(ICCC).Chengdu:IEEE,2019:1975-1979.[12]QIANGZK,YANTF,TANGCY.DemodulationofLowSNRQPSKSignalBasedonCNN[C]ʊ2021InternationalConferenceonIntelligentTransportation,BigData&SmartCity(ICITBS).Xi an:IEEE,2021:638-641.[13]ZHANGL,ZHANGH,JIANGY,etal.IntelligentandReliableDeepLearningLSTMNeuralNetworks⁃basedOFDM⁃DCSKDemodulationDesign[J].IEEETransactionsonVehicularTechnology,2020,69(12):16163-16167.[14]KOZLENKOM,LAZAROVYCHI,TKACHUKV,etal.SoftwareDemodulationofWeakRadioSignalsUsingCon⁃volutionalNeuralNetwork[C]ʊ2020IEEE7thInterna⁃tionalConferenceonEnergySmartSystems(ESS).Kyiv:IEEE,2020:339-342.[15]孙柏昶,陈超群.MFSK调制方式在极低速通信中的性能分析[J].无线电通信技术,2019,45(2):182-185.[16]邓琪,高建军,葛冬冬,等.现代优化理论与应用[J].中国科学:数学,2020,50(7):899-968.[17]高勇,黄振,陆建华.基于小波变换的MFSK信号盲解调算法[J].装备指挥技术学院学报,2010,21(1):82-87.[18]沈越泓,钱祖平,益晓新.新型MFSK最佳相干解调器[J].电子科学学刊,2000,22(4):573-578.[19]董鑫,欧阳喜,李斌.一种衰落信道下MFSK信号符号速率估计算法[J].数据采集与处理,2015,30(5):1121-1130.作者简介:㊀㊀李㊀濛㊀硕士研究生㊂主要研究方向:无线通信㊁信号调制解调㊂㊀㊀(∗通信作者)吴呈瑜㊀讲师㊂主要研究方向:认知无线网络中的无线资源管理㊁5G超密集网络㊂㊀㊀占㊀敖㊀讲师㊂主要研究方向:协同通信㊁无线网络编码和多中继网络容量分析㊂。
一、引言MFSK(多频正交调信号)是一种广泛使用的数字调制技术,广泛应用于无线通信、卫星通信等领域。
Matlab提供了一种名为MFSK的函数,用于实现MFSK调制和解调。
本文将介绍MFSK函数的基本原理和实现方法。
二、MFSK调制原理MFSK调制是一种基于正交调的数字调制技术,其基本原理是将数字信息加载到正弦和余弦两个信号上,然后将它们叠加在一起形成调制信号。
具体来说,MFSK调制包括以下几个步骤:1.生成基带数字信号,通常采用二进制相移键控(BPSK)或二进制频移键控(BFSK)等数字调制技术。
2.将数字信号映射到正弦和余弦两个信号上,生成两个正交调制信号。
3.将两个正交调制信号叠加在一起形成调制信号。
4.通过滤波器将调制信号转换为中频信号。
5.通过信道传输中频信号,接收端进行解调,恢复原始数字信号。
MFSK调制具有较高的频带利用率和较好的抗干扰性能,因此在无线通信和卫星通信等领域得到了广泛应用。
Matlab中的MFSK函数可以实现MFSK调制和解调。
以下是MFSK 函数的实现原理:1.输入参数:MFSK函数需要输入两个参数,一个是数字基带信号,另一个是调制阶数N。
数字基带信号可以是BPSK或BFSK等数字调制信号,调制阶数N决定了MFSK调制的阶数。
2.生成正弦和余弦两个信号:根据输入的数字基带信号和调制阶数N,MFSK函数会生成两个正交调制信号。
具体来说,每个信号由一个线性方程生成的相位序列得到相位值,通过映射得到不同的振幅值,得到模拟的波形。
3.叠加调制信号:将两个正交调制信号叠加在一起形成调制信号。
在叠加过程中,两个信号会进行适当的相位偏移和滤波处理,以获得更好的性能。
4.传输和解调:将调制信号通过信道传输,接收端通过滤波和解调,恢复原始数字基带信号。
在解调过程中,可以使用MFSK函数提供的解调算法对接收到的中频信号进行解调和解码,恢复原始数字信息。
需要注意的是,MFSK函数的具体实现可能会因Matlab版本和设置的不同而有所差异。
目录前言1正文22.1 课程设计的目的与意义22.2 多进制数字调制22.3 MFSK简介22.4 MFSK信号的频谱、带宽与频带利用率32.5 MFSK调制与解调的原理43 仿真结果与分析53.1 八进制的随机序列53.2 调制后的信号63.3 参加高斯白噪声后的已调信号73.4 MFSK的解调83.4.1 滤除高斯白噪声83.4.2 相干解调后的信号83.4.3 非相干解调后的信号93.5 MFSK系统的抗噪声性能103.5.1 相干解调时的误码率103.5.2 非相干解调时的误码率11课程设计总结12致谢12参考文献12附录14前言MFSK——多进制数字频率调制,简称多频制,是2FSK方式的推广。
它是用不同的载波频率代表各种数字信息。
在数字通信系统中,数字调制与解调技术占有非常重要的地位。
随着MATLAB技术的开展,数字通信技术与MATLAB的结合表现了现代数字通信系统开展的一个趋势。
文中介绍了MFSK调制解调的原理,并基于MATLAB实现MFSK调制解调的程序代码设计,仿真结果明确设计方案是可行的。
正文2.1 课程设计的目的与意义本次课程设计我所做的课题是一个多进制频移键控MFSK的调制与解调项目,这就要求我们需要完成信号的调制解调以与抗噪声性能的分析等问题。
通过我们对这次项目的学习和理解,综合运用课本中所学到的理论知识完成一个多进制频移键控MFSK的调制与解调项目的课程设计。
以与锻炼我们查阅资料、方案比拟、团结合作的能力。
学会了运用MATLAB编程来实现MFSK调制解调过程,并且输出其调制与解调过程中的波形,并且讨论了其调制和解调效果,分析了抗噪声性能,增强了我的动手能力,为以后学习和工作打下了根底。
2.2 多进制数字调制二进制键控调制系统中,每个码元只传输1b信息,其频带利用率不高。
而频率资源是极其宝贵和紧缺的。
为了提高频带利用率,最有效的方法是使一个码元传输多个比特的信息。
这就是将要讨论的多进制键控体制。
多进制数字相位调制(MPSK)1前言:VHDL主要用于描述数字系统的结构,行为,功能和接口。
除了含有许多具有硬件特征的语句外,VHDL的语言形式和描述风格与句法是十分类似于一般的计算机高级语言。
VHDL的程序结构特点是将一项工程设计,或称设计实体(可以是一个元件,一个电路模块或一个系统)分成外部(或称可是部分,及端口)和内部(或称不可视部分),既涉及实体的内部功能和算法完成部分。
在对一个设计实体定义了外部界面后,一旦其内部开发完成后,其他的设计就可以直接调用这个实体。
这种将设计实体分成内外部分的概念是VHDL系统设计的基本点。
2设计主题2.1设计目的(1).掌握MPSK的设计原理(2).掌握MPSK的VHDL设计2.2 MPSK的设计原理多进制数字相位调制也称多元调相或多相制。
它利用具有多个相位状态的正弦波来代表多组二进制信息码元,即用载波的一个相位对应于一组二进制信息码元。
如果载波有2k个相位,它可以代表 k位二进制码元的不同码组。
多进制相移键控也分为多进制绝对相移键控和多进制相对(差分)相移键控。
下面以四相相位调制为例进行讨论。
四相调相信号是一种四状态符号,即符号有00、01、10、11四种状态。
所以,对于输入的二进制序列,首先必须分组,每两位码元一组。
然后根据组合情况,用载波的四种相位表征它们。
这种由两个码元构成一种状态的符号码元称为双比特码元。
同理,k位二进制码构成一种状态符号的码元则称为k比特码元、四相PSK(4PSK)信号实际是两路正交双边带信号。
串行输入的二进制码,两位分成一组。
若前一位用A表示,后一位用B表示,经串/并变换后变成宽度加倍的并行码(A、B码元在时间上是对齐的)。
再分别进行极性变换,把单极性码变成双极性码,然后与载波相乘,形成正交的双边带信号,加法器输出形成4PSK信号。
显然,此系统产生的是π/4系统PSK信号。
如果产生π/2系统的PSK信号,只需把载波移相π/4后再加到乘法器上即可。
甚低频通信的 MSK与 MFSK性能比较分析甚低频通信技术是一种应用于超长距离无线通信的技术,其工作频率位于30Hz到300Hz之间。
在此频率范围内,甚低频通信技术具有穿透力强、适用于远距离无线通信等优点,但由于其传输速率较慢,因此需要一种高效的调制方式来实现数据传输。
最常用的两种调制方式是MSK和MFSK,本文将对它们进行比较分析。
MSK(Minimum Shift Keying)调制方式是一种将数字信号转换为模拟信号的变换方法。
它通过改变载波的相位来实现数字信号的传输。
MSK调制在传输时将数据编解码后,采用不同的相位角度去划分两个不同的数字信号,从而实现数据的传输。
它的优点是能够有效地降低频谱带宽,达到高速数据传输的目的,但也存在着一个缺点,即在新型的多接收器/多传输器网络中,它难以减少同步问题,也难以实现复杂的调制方式。
MFSK(Multiple Frequency Shift Keying)调制方式也是一种将数字信号转换为模拟信号的变换方法。
它通过改变载波的频率来实现数字信号的传输。
MFSK调制通常采用两种不同的频率,将数字信号编码成二进制数据,然后将这两种不同的频率作为载波频率,实现数据的传输。
它的优点是可以通过选择适当的频率带宽来实现高速数据传输,同时还可以减少同步的问题。
但是MFSK在频率选择方面有一定的局限性,会受到噪声的影响。
因此,从速度和可靠性角度来看,MSK和MFSK分别具有其独特的优点和缺点。
在实际应用中,需要根据不同的情况来应用相应的调制方式。
当需要高速传输数据时,MSK更加适用;而在传输距离较远或存在噪声的情况下,MFSK更加稳定可靠。
此外,对于新型的多接收器/多传输器网络,需要考虑同步问题,因此MFSK更加适用。
在总体而言,MSK和MFSK都是基于相位或频率变化来实现数字信号的调制方式,其各自的优缺点与实际应用相关。
未来,它们将继续拓展其应用领域,为超长距离无线通信提供更加完善的解决方案。
目录前言 (1)正文 (1)2.1 课程设计的目的及意义 (1)2.2 多进制数字调制 (1)2.3 MFSK简介 (1)2.4 MFSK信号的频谱、带宽及频带利用率 (2)2.5 MFSK调制与解调的原理 (3)3 仿真结果与分析 (3)3.1 八进制的随机序列 (3)3.2 调制后的信号 (4)3.3 加入高斯白噪声后的已调信号 (5)3.4 MFSK的解调 (6)3.4.1 滤除高斯白噪声 (6)3.4.2 相干解调后的信号 (7)3.4.3 非相干解调后的信号 (7)3.5 MFSK系统的抗噪声性能 (8)3.5.1 相干解调时的误码率 (8)3.5.2 非相干解调时的误码率 (8)课程设计总结 (9)致谢 (9)参考文献 (10)附录 (11)前言MFSK——多进制数字频率调制,简称多频制,是2FSK方式的推广。
它是用不同的载波频率代表各种数字信息。
在数字通信系统中,数字调制与解调技术占有非常重要的地位。
随着MATLAB技术的发展,数字通信技术与MATLAB的结合体现了现代数字通信系统发展的一个趋势。
文中介绍了MFSK调制解调的原理,并基于MATLAB实现MFSK调制解调的程序代码设计,仿真结果表明设计方案是可行的。
正文2.1 课程设计的目的及意义本次课程设计我所做的课题是一个多进制频移键控MFSK的调制与解调项目,这就要求我们需要完成信号的调制解调以及抗噪声性能的分析等问题。
通过我们对这次项目的学习和理解,综合运用课本中所学到的理论知识完成一个多进制频移键控MFSK的调制与解调项目的课程设计。
以及锻炼我们查阅资料、方案比较、团结合作的能力。
学会了运用MATLAB编程来实现MFSK调制解调过程,并且输出其调制及解调过程中的波形,并且讨论了其调制和解调效果,分析了抗噪声性能,增强了我的动手能力,为以后学习和工作打下了基础。
2.2 多进制数字调制二进制键控调制系统中,每个码元只传输1b信息,其频带利用率不高。
而频率资源是极其宝贵和紧缺的。
为了提高频带利用率,最有效的办法是使一个码元传输多个比特的信息。
这就是将要讨论的多进制键控体制。
多进制键控体制可以看作是二进制键控体制的推广。
这时,为了得到相同的误码率,和二进制系统相比,接要用更大的发送信号功率。
这就是为了传输更多信息量所要付出的代价。
由二进制数字调制系统的性能比较可得知,各种键控体制的误码率都决定于信噪比:r=a 22σn2(r表示信号码元收信号信噪比需要更大,即需码元功率a 22和噪声功率σn2之比)。
现在,设多进制码元的进制数为M,一个码元中包含信息K比特,则有k=log2M;若想把码元功率a 22平均分配给每比特,则每比特分得的功率为P b=a22k;这样每比特的信噪功率比为:r b=rk;在M进制中,由于每个码元包含的比特数K和进制数M有关,所以在研究不同M值下的错误率时,适合用r b为单位来比较不同体制的性能优劣。
所谓多进制数字调制,就是利用多进制数字基带信号去调制高频载波的某个参量,如幅度、频率或相位的过程。
根据被调参量的不同,多进制数字调制可分为多进制幅度键控(MASK)、多进制频移键控(MFSK)以及多进制相移键控(MPSK或MDPSK)。
也可以把载波的两个参量组合起来进行调制,如把幅度和相位组合起来得到多进制幅相键控(MAPK)或它的特殊形式多进制正交幅度调制(MQAM)等。
2.3 MFSK简介多进制数字频率调制(MFSK)简称多频制,是2FSK方式的推广。
它是用不同的载波频率代表不同种数字信息。
多进制频移键控(MFSK)的基本原理和2FSK是相同的,其调制可以用频率键控法和模拟调频电路来实现,不同之处在于使用键控法的时候供选的频率有M个。
MFSK(多进制频移键控),是一种在各种频率离散音频脉冲爆发传送数字信息的信号调制方法。
它原来是欧洲和英国政府机构在20世纪中叶使用。
在那时它叫做Piccolo,一种乐器的名字,这种乐器的声音音调很高,就像一个MFSK信号经过收音机的喇叭时发出的声音。
MFSK的主要缺点是信号占用较宽的频带,信道频带利用率不高。
因此MFSK一般用于调制速率(1T B) 不高的衰落信道传输场合。
2.4 MFSK信号的频谱、带宽及频带利用率键控法产生的MFSK信号,可以看作由M个幅度相同、载频不同、时间上互不重叠的2ASK信号叠加的结果。
设MFSK信号码元的宽度为T B,即传输速率f B=1T B(Baud),则MFSK信号的带宽为B=|f M−f1|+∆f;式中为f M最高选用载频,f1为最低选用载频。
∆f为单个码元的带宽。
MFSK信号功率谱P(f)如图2-4所示:图2-4 MFSK信号的功率谱若相邻载频之差等于2B f,即相邻频率的功率谱主瓣刚好互不重叠,这时的MFSK信号的带宽及频带利用率分别为:B MFSK=2Mf B n=Kf BB MFSK =K2M=log2M2M式中M=2K,K=2,3,……。
可见,MFSK信号的带宽随频率数的增大而线性增宽,频带利用率明显下降。
因此,MFSK多用于调制速率较低及多径延时比较严重的信道,如无线短波信道。
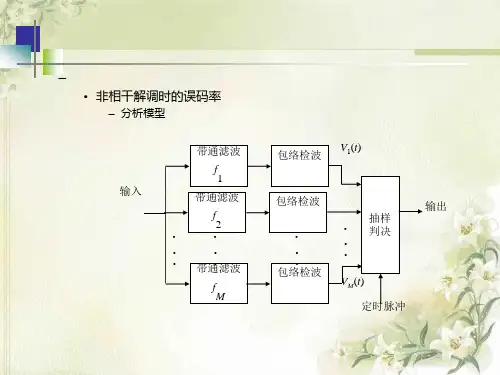
2.5 MFSK调制与解调的原理图2-5 多进制数字频率调制系统的组成方框图MFSK调制原理和2FSK的基本相同。
串/并变换器和逻辑电路1将一组组输入的二进制码(每K 个码元为一组)对应地转换成有M(M=2K)种状态的一个个多进制码。
这M个状态分别对应M个不同的载波频率(f1,f2……fm)。
要求载频之间的距离足够大,以便用滤波器分离不同频率的谱。
当某组K位二进制码到来时,逻辑电路1的输出一方面接通某个门电路,让相应的载频发送出去,另一方面同时关闭其余所有的门电路。
于是当一组二进制码元输入时,经相加器组合输出的便是一个M进制调频波形。
多进制频移键控的解调部分由M个带通滤波器BPF、包络检波器及一个抽样判决器、逻辑电路2组成。
各带通滤波器的中心频率分别对应发送端的各个载波频率。
因而,当某一已调信号到来时,在任一码元持续时间内,只有与发送端频率相应的一个带通滤波器能收到信号,其它带通滤波器只有噪声通过。
抽样判决器的任务是比较所有检波器输出的电压,并选出最大者作为输出,这个输出是一位与发送端载波频率相应的进制数M。
逻辑电路2把这个M进制数译成K位二进制并行码,并进一步做并/串变换恢复二进制信息输出,从而完成数字信号的传输。
3 仿真结果与分析3.1 八进制的随机序列在本次课程设计中M=8,所以是每3个码元为一组,这8个状态分别对应8个不同的载波频率。
8FSK采用8种不同的频率分别表示三比特信息。
如图3-1所示:图3-1 二进制随机序列的产生程序的运行过程是:首先产生随机序列码(如图3-1所示 注:此序列为随机序列,每一次运行程序所产生的序列都不同。
)表3-1 M=8时的码元 3.2 调制后的信号图3-2-1 调制后的信号02468101214八进制随机序列T ime 码元已调信号的眼图如3-2-1图所示图3-2-2 未加入高斯白噪声已调信号的眼图由图3-2-2可知眼图的线迹是比较清晰的带状的线,线条较细,清晰,“眼睛”张开的大,说明未加入高斯白噪声的已调信号码间串扰比较小。
3.3 加入高斯白噪声后的已调信号然后通过调用函数对随机序列进行调制,如图3-3-1所示。
在调制信号中加入高斯白噪声如图6所示。
图3-3-1 加入高斯白噪声的已调信号在实际中,只要噪声的功率谱均匀分布的频率范围远远大于通信系统的工作频带,我们就可以把它视为白噪声。
如果白噪声取值的概率服从高斯分布,则称为高斯白噪声。
加入高斯白噪声后已调信号的眼图如下图3-3-2所示:图3-3-2 加入高斯白噪声后已调信号的眼图由图可知眼图的线迹是比较模糊的带状的线,线条较粗,模糊,“眼睛”张开的小,说明加入高斯白噪声的已调信号噪声大,码间串扰比较大。
3.4 MFSK的解调3.4.1 滤除高斯白噪声图3-4-1 升余弦滤波器前后波形比较图3-4-1中红线表示:加入高斯白噪声的已调信号;蓝线表示:经过升余弦滤波器后的已调信号。
升余弦滤波器本质上是一个低通滤波器,滤除了高频成分,减小了码间串扰和噪声。
只不过是他的滚降因子会对波形的幅度产生一定影响,一般是降低了波形的幅度并且低通。
减小了码间串扰和噪声。
3.4.2 相干解调后的信号在通过调用函数让函数通过相干解调方式进行解调,解调信号如图3-4-2所示图3-4-2 相干解调后的信号原序列比较因为MFSK信号占用较宽的带宽,频带利用率不高,所以MFSK一般用于调制速率不高的衰落信号的传输场合,这些信道会引起信号的相位和振幅随机抖动和起伏。
余弦滚降滤波器只能减小码间串扰和定时误差的影响,不能完全消除噪声,所以相干解调后的信号与原信号存在误差。
3.4.3 非相干解调后的信号在通过调用函数让函数通过非相干解调方式进行解调,解调信号如图3-4-3所示图3-4-3 非相干解调后的信号原序列比较因为MFSK信号占用较宽的带宽,频带利用率不高,所以MFSK一般用于调制速率不高的衰落信号的传输场合,这些信道会引起信号的相位和振幅随机抖动和起伏。
余弦滚降滤波器只能减小码间串扰和定时误差的影响,不能完全消除噪声,所以非相干解调后的信号与原信号也存在误差。
3.5 MFSK系统的抗噪声性能3.5.1 相干解调时的误码率图3-5-1 相干解调后误码率统计注释:图3-5-1中右上角的意思为:绿线表示二进制误码率和信噪比之间的关系,红线表示八进制误码率和信噪比之间的关系。
在相同误码率的情况下,随着进制数M的增大信噪比减小;在相同信噪比的情况下,随着进制数M的增大误码率减小。
MFSK信号采用相干解调(相干检波器)时系统的误码率为上界公式为:P e≤(M−1)erfc(√r);可以看出,多频制误码率随M增大而减小,但与多电平调制相比增加的速度要小的多。
所以MFSK信号在相干解调时的设备复杂,应用较少。
3.5.2 非相干解调时的误码率图3-5-2 非相干解调后误码率统计注释:图3-5-2中右上角的意思为:绿线表示二进制误码率和信噪比之间的关系,红线表示八进制误码率和信噪比之间的关系。
在相同误码率的情况下,随着进制数M的增大信噪比减小;在相同信噪比的情况下,随着进制数M的增大误码率减小。
MFSK信号采用非相干解调时(包络检波器)系统的误码率为:P e≈M−12e−r2;式中r为平均信噪比。
r b=rlog2M为每比特的信噪功率比。
M=8,K=3,如表3-1所示,在任一一列中均有4个“0”和4个“1”。
所以在给定的比特位置上的信息和其他(2K−1−1)种码元在同一位置上的信息相同,和其他2k−1种码元在同一位置上的信息则不同。
所以比特错误率P b和码元错误率P e之间的关系为:P b=2k−12k−1P e=P e2[1−12k];当K很大时,P b≈P e2。