浙江省中小学生研学实践教育基地(第二批)公示名单(43家)
- 格式:doc
- 大小:191.50 KB
- 文档页数:7
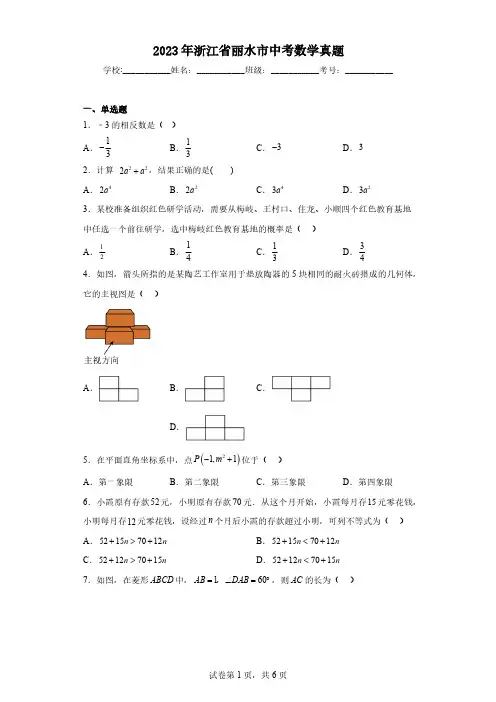
2023年浙江省丽水市中考数学真题学校:___________姓名:___________班级:___________考号:___________A .....在平面直角坐标系中,点()21,1P m -+位于(A.12B.18.如果100N的压力F作用于物体上,产生的压强力面积()2S m的说法正确的是()A.S小于20.1m B.S大于0.1mA.2B.2 2二、填空题11.分解因式:x2-9=______.12.青田县“稻鱼共生”种养方式因稻鱼双收、互惠共生而受到农户青睐,现有一农户在5块面积相等的稻田里养殖田鱼,产量分别是(单位:kg):12,13,15,17,18,则这5块稻田的田鱼平均产量是__________kg.13.如图,在ABC中,AC的垂直平分线交BC于点D,交AC于点E,B ADB∠=∠.若4AB=,则DC的长是__________.14.小慧同学在学习了九年级上册“4.1比例线段”3节课后,发现学习内容是一个逐步特殊化的过程,请在横线上填写适当的数值,感受这种特殊化的学习过程.图中横线处应填:__________15.古代中国的数学专著《九章算术》中有一题:“今有生丝三十斤,干之,耗三斤十二两.今有干丝一十二斤,问生丝几何?”意思是:“今有生丝30斤,干燥后耗损3斤12两(古代中国1斤等于16两).今有干丝12斤,问原有生丝多少?”则原有生丝为__________斤.16.如图,分别以,,,a b m n 为边长作正方形,已知m n >且满足2am bn -=,4an bm +=.(1)若3,4a b ==,则图1阴影部分的面积是__________;(2)若图1阴影部分的面积为3,图2四边形ABCD 的面积为5,则图2阴影部分的面积是__________.三、解答题20.为全面提升中小学生体质健康水平,我市开展了儿童青少年专家组随机抽取某校各年级部分学生进行了脊柱健康状况筛查.绘制了两幅不完整的统计图表,请根据图表信息解答下列问题:抽取的学生脊柱健康情况统计表(2)该校共有学生1600人,请估算脊柱侧弯程度为中度和重度的总人数;(3)为保护学生脊柱健康,请结合上述统计数据,提出一条合理的建议.21.我市“共富工坊”问海借力,某公司产品销售量得到大幅提升.为促进生产,公司提供了两种付给员工月报酬的方案,如图所示,员工可以任选一种方案与公司签订合同.看图解答下列问题:(1)直接写出员工生产多少件产品时,两种方案付给的报酬一样多;(2)求方案二y 关于x 的函数表达式;(3)如果你是劳务服务部门的工作人员,你如何指导员工根据自己的生产能力选择方案.22.某数学兴趣小组活动,准备将一张三角形纸片(如图)进行如下操作,并进行猜想和证明.(1)用三角板分别取,AB AC 的中点,D E ,连接DE ,画AF D E ⊥于点F ;(2)用(1)中所画的三块图形经过旋转或平移拼出一个四边形(无缝隙无重叠),并用三角板画出示意图;(3)请判断(2)中所拼的四边形的形状,并说明理由.23.已知点(),0m -和()3,0m 在二次函数23,(y ax bx a b =++是常数,0)a ≠的图像上.(1)当1m =-时,求a 和b 的值;(2)若二次函数的图像经过点(),3A n 且点A 不在坐标轴上,当21m -<<-时,求n 的取值范围;(3)求证:240b a +=.24.如图,在O 中,AB 是一条不过圆心O 的弦,点,C D 是 AB 的三等分点,直径CE 交AB 于点F ,连结AD 交CF 于点G ,连结AC ,过点C 的切线交BA 的延长线于点H .(1)求证: AD HC ∥;(2)若2OG GC=,求tan FAG ∠的值;(3)连结BC 交AD 于点N ,若O ①若52OF =,求BC 的长;②若10AH =,求ANB 的周长;参考答案:∵四边形ABCD 是菱形,∴AB CD ∥,AB AD =,AC BD ⊥由圆周角定理得:90BDE ∠=︒,ADB ∠45ADB C CBD ∴∠=∠=∠=︒,45ABD DBE EBC DBE ∴∠+∠=︒=∠+∠ABD EBC ∠=∠∴,ADB C ∠=∠⎧【点睛】本题主要考查解一元一次不等式组,掌握不等式的性质,解一元一次不等式的方法是解题的关键.19.18m【分析】如图:过点D 作DE AB ⊥于点E ,由题意易得4BE CD ==,进而求得7AE =,再通过解直角三角形可得cos6014AD AE =÷︒=,然后求出AD CD +即可解答.【详解】解:如图:过点D 作DE AB ⊥于点E ,由题意,得4BE CD ==,∵11AB =,∴7AE =.∵60A ∠=︒,∴cos6014AD AE =÷︒=.∴()18m AD CD +=.即管道A D C --的总长为18m .【点睛】本题主要考查了解直角三角形的应用,理解题意求得cos6014AD AE =÷︒=是解答本题的关键.20.(1)200人(2)80人(3)答案不唯一,见解析【分析】(1)利用抽取的学生中正常的人数除以对应的百分比即可得到所抽取的学生总人数;(2)用该校学生总数乘以抽取学生中脊柱侧弯程度为中度和重度的百分比即可得到答案;(3)利用图表中的数据提出合理建议即可.【详解】(1)解:17085%200÷=(人).∴所抽取的学生总人数为200人.(2)()1600185%10%80⨯--=(人).∴估算该校学生中脊柱侧弯程度为中度和重度的总人数有80人.(3)该校学生脊柱侧弯人数占比为15%,说明该校学生脊柱侧弯情况较为严重,建议学校要每天组织学生做护脊操等.【点睛】此题考查了统计表和扇形统计图,熟练掌握用部分除以对应的百分比求总数、用样本估计总体是解题的关键.21.(1)30件(2)20600y x =+(3)若每月生产产品件数不足30件,则选择方案二;若每月生产产品件数就是30件,两种方案报酬相同,可以任选一种;若每月生产产品件数超过30件,则选择方案一【分析】(1)由图象的交点坐标即可得到解答;(2)由图象可得点()()0,600,30,1200,设方案二的函数表达式为y kx b =+,利用待定系数法即可得到方案二y 关于x 的函数表达式;(3)利用图象的位置关系,结合交点的横坐标即可得到结论.【详解】(1)解:由图象可知交点坐标为()30,1200,即员工生产30件产品时,两种方案付给的报酬一样多;(2)由图象可得点()()0,600,30,1200,设方案二的函数表达式为y kx b =+,把()()0,600,30,1200代入上式,得600,301200.b k b =⎧⎨+=⎩解得20,600.k b =⎧⎨=⎩∴方案二的函数表达式为20600y x =+.(3)若每月生产产品件数不足30件,则选择方案二;若每月生产产品件数就是30件,两种方案报酬相同,可以任选一种;若每月生产产品件数超过30件,则选择方案一.【点睛】此题考查了从函数图像获取信息、一次函数的应用等知识,从函数图象获取正确信息和掌握待定系数法是解题的关键.22.(1)见解析(2)见解析(3)答案不唯一,见解析【分析】(1)根据题意画出图形即可;(2)方法一:将ADF △绕点D 逆时针旋转180︒到DBM △,将AEF △绕E 点逆时针旋转180︒到CEN 即可得出四边形BCNM ;方法二:将AEF △绕E 点逆时针旋转180︒到CEM ,将ADF △绕点D 逆时针旋转180︒后再沿BC 向右平移到CMN ,即可得出四边形DBCN ;方法三:将ADF △绕点D 逆时针旋转180︒到DBN ,将AEF △绕E 点逆时针旋转180︒后沿CB 向左平移到BNM ,即可得出四边形MBCE ;(3)方法一:先证明点,,,M D E N 在同一直线上,根据DE 为ABC 的中位线,得出DE BC ∥且2BC DE =.证明MN MD DE EN BC =++=且MN BC ∥,得出四边形MBCN 为平行四边形,根据90M ∠=︒,得出平行四边形MBCN 为矩形.方法二:证明点,,,D E M N 在同一直线上,根据DE 为ABC 的中位线,得出DE BC ∥且2BC DE =,证明EN DE =,得出DN BC =且DN BC ∥,证明四边形DBCN 为平行四边形.方法三:证明点,,,M N D E 在同一直线上,根据DE 为ABC 的中位线,得出DE BC ∥且2BC DE =,证明ME BC =且ME BC ∥,得出四边形MBCE 为平行四边形.【详解】(1)解:如图所示:(2)解:方法一:四边形BCNM 为所求作的四边形方法二:四边形DBCN 是所求的四边形.方法三:四边形MBCE 是所求的四边形.(3)解:方法一(图1),∵180,180MDB BDE DEC NEC ∠+∠=︒∠+∠=︒,∴点,,,M D E N 在同一直线上,∵点,D E 分别是,AB AC 的中点,∴DE 为ABC 的中位线,∴DE BC ∥且2BC DE =.∵MD EN DE +=,∴MN MD DE EN BC =++=且MN BC ∥,∴四边形MBCN 为平行四边形.∵AF D E ⊥,90M ∠=︒,∴平行四边形MBCN 为矩形.方法二(图2),∵180,180DEC MEC EMC NMC ∠+∠=︒∠+∠=︒,∴点,,,D E M N 在同一直线上.∵点,D E 分别是,AB AC 的中点,∴DE 为ABC 的中位线,∴DE BC ∥且2BC DE =.∵EN DE =,∴DN BC =且DN BC ∥,∴四边形DBCN 为平行四边形.方法三(图3),∵180,180MNB BND NDB BDE ∠+∠=︒∠+∠=︒,∴点,,,M N D E 在同一直线上.∵点,D E 分别是,AB AC 的中点,∴DE 为ABC 的中位线,∴DE BC ∥且2BC DE =.∵MD DE =,∴ME BC =且ME BC ∥,∴四边形MBCE 为平行四边形.【点睛】本题主要考查了旋转作图或平移作图,平行四边形的判定,矩形的判定,解题的关键熟练掌握旋转的性质和平移的性质.23.(1)1,2a b =-=-(2)42n -<<-(3)见解析【分析】(1)由1m =-可得图像过点()1,0和()3,0-,然后代入解析式解方程组即可解答;(2)先确定函数图像的对称轴为直线x m =,则抛物线过点()(),3,0,3n ,即2n m =,然后再结合21m -<<-即可解答;∴BAD CAD ∠=∠.由CE AD ⊥,则AGF AGC ∠=∠又∵AG AG =,∴CAG FAG △≌△,∴CG FG =.设CG a =,则FG a =,2OG =∵,AD HC FG GC =∥,∴AH AF =.∵90HCF ∠=︒,∴10AC AH AF ===.设CG x =,则,5FG x OG ==-由勾股定理得222AG AO OG =-设CG x =,则,5FG x OG ==-由勾股定理得222AG AO OG =-2222210AF AG FG x x x =+=-+∵,AD HC FG GC =∥,∴12AH AF HF ==,∴12AG HC =.。

研学旅游六年级作文(优秀7篇)(经典版)编制人:__________________审核人:__________________审批人:__________________编制单位:__________________编制时间:____年____月____日序言下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!并且,本店铺为大家提供各种类型的经典范文,如工作资料、求职资料、报告大全、方案大全、合同协议、条据文书、教学资料、教案设计、作文大全、其他范文等等,想了解不同范文格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor.I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, this shop provides you with various types of classic model essays, such as work materials, job search materials, report encyclopedia, scheme encyclopedia, contract agreements, documents, teaching materials, teaching plan design, composition encyclopedia, other model essays, etc. if you want to understand different model essay formats and writing methods, please pay attention!研学旅游六年级作文(优秀7篇)在日常的学习、工作、生活中,大家总少不了接触作文吧,作文是人们以书面形式表情达意的言语活动。

第1篇一、案例一:信息技术与教育教学深度融合案例背景:随着信息技术的飞速发展,我国教育领域正经历着前所未有的变革。
为推进信息技术与教育教学的深度融合,某中学开展了“智慧课堂”试点项目。
案例内容:1. 教师通过学习平台获取教学资源,结合信息技术手段,设计丰富多彩的教学活动,提高学生的学习兴趣。
2. 学生利用平板电脑、笔记本电脑等设备,在课堂上进行自主学习、互动交流,提高学习效率。
3. 教师通过教学平台实时监控学生的学习进度,针对性地进行辅导,实现个性化教学。
案例成效:1. 学生学习成绩显著提高,学习兴趣得到激发。
2. 教师教育教学水平得到提升,教学质量得到保证。
3. 促进了信息技术与教育教学的深度融合,为我国教育事业发展提供了有力支持。
二、案例二:农村教育振兴行动计划案例背景:为缩小城乡教育差距,提高农村教育质量,我国政府启动了农村教育振兴行动计划。
案例内容:1. 加大对农村学校的投入,改善教学设施,提高教师待遇。
2. 加强农村教师队伍建设,开展教师培训,提高教师素质。
3. 推进城乡教育资源共享,组织城市优秀教师到农村学校支教。
案例成效:1. 农村学校教育教学质量得到显著提高,学生综合素质得到提升。
2. 农村教育基础设施得到改善,学校面貌焕然一新。
3. 城乡教育差距逐渐缩小,为我国教育事业发展奠定了坚实基础。
三、案例三:职业教育与产业深度融合案例背景:为满足经济社会发展需求,我国职业教育正朝着与产业深度融合的方向发展。
案例内容:1. 职业院校与企业合作,共同制定人才培养方案,培养适应产业需求的高素质技术技能人才。
2. 职业院校与企业共建实训基地,为学生提供真实的工作环境,提高学生实践能力。
3. 职业院校与企业开展产学研合作,推动科技成果转化,服务经济社会发展。
案例成效:1. 职业教育人才培养质量得到提高,毕业生就业率显著提升。
2. 企业得到高素质技术技能人才支持,促进了产业发展。
3. 职业教育为我国经济社会发展提供了有力的人才保障。

落实“双减”政策致家长的⼀封信(精选25篇)落实“双减”政策致家长的⼀封信 ⼀、书信简介 书信分为⼀般书信和专⽤书信两⼤类。
⼀般书信主要有家庭成员之间的家书类书信,朋友和同事之间的问候类书信、请托类书信、规劝类书信、借贷类书信、庆贺类书信等。
这类书信多⽤于个⼈和个⼈之间。
专⽤书信主要有表扬信、感谢信、邀请信等。
这类书信多⽤于单位与⼈、单位与单位之间。
⼀般书信由信封和信瓤两部分组成。
信封是显⽰于外的东西,信瓤则是信的正⽂。
信封分为竖式信封与横式信封两种。
⼆、落实“双减”政策致家长的⼀封信(精选25篇) ⽆论是⾝处学校还是步⼊社会,⼤家对书信都再熟悉不过了吧,书信是⼈们相互交流情感与思想的⼯具。
写起信来就毫⽆头绪?下⾯是⼩编为⼤家收集的落实“双减”政策致家长的⼀封信(精选25篇),供⼤家参考借鉴,希望可以帮助到有需要的朋友。
落实“双减”政策致家长的⼀封信1亲爱的家长朋友们: 《关于进⼀步减轻义务教育阶段学⽣作业负担和校外培训负担的意见》明确严格执⾏未成年⼈保护法有关规定,校外培训机构不得占⽤国家法定节假⽇、休息⽇及寒暑假期组织学科类培训。
学校要充分利⽤资源优势,提升学校课后服务⽔平,满⾜学⽣多样化需求;⼤⼒提升教育教学质量,确保学⽣在校内学⾜学好。
《意见》还对家校协同育⼈共同体建设提出指导建议,推动形成减负共识。
为有效落实“双减”⼯作,减轻中⼩学⽣校内校外负担,结合当前疫情防控⼯作要求,温馨提醒如下: ⼀、慎重选报培训课程 XX区教体局严格执⾏省、市关于学科类培训机构管理统⼀部署。
为保障⾃⾝利益,家长们⼀定要和培训机构签订培训合同(参照《中⼩学⽣校外培训合同(⽰范⽂本)》),希望家长谨慎报名学科类培训机构,谨慎付(续)费,以免发⽣不必要的退费纠纷。
⾮学科类的兴趣爱好培训,也请家长根据孩⼦实际情况,适度参加。
学科类指中⼩学语⽂、数学、外语、物理、化学等⽂化学科及与其升学考试相关的延伸类项⽬,具体包括道德与法治、语⽂、历史、地理、数学、外语(英语、⽇语、俄语)、物理、化学、⽣物等。

第1篇一、引言基础教育是我国教育体系的重要组成部分,关系到国家未来人才培养的质量。
近年来,我国基础教育领域不断涌现出各种创新案例,为我国基础教育改革与发展提供了有益借鉴。
本文将针对基础教育领域的若干典型案例进行汇总分析,以期为广大教育工作者提供有益参考。
二、基础教育案例汇总1. 案例一:北京市某小学“快乐课堂”教学实践背景:为了提高学生的学习兴趣,该校教师创新教学方式,将“快乐课堂”理念融入教学实践。
措施:教师采用小组合作、角色扮演、游戏化教学等方法,激发学生的学习兴趣,让学生在轻松愉快的氛围中学习。
效果:学生的课堂参与度明显提高,学习成绩和综合素质得到提升。
2. 案例二:上海市某中学“翻转课堂”教学模式探索背景:为了提高学生的学习效率,该校教师尝试采用“翻转课堂”教学模式。
措施:教师将课堂讲授内容提前录制视频,学生课前自主学习,课堂上进行讨论、实践和巩固。
效果:学生的学习主动性得到提高,课堂效率显著提升。
3. 案例三:浙江省某农村小学“一校一品”特色发展之路背景:该校地处偏远农村,教育资源相对匮乏。
为了提高教育质量,该校校长带领教师探索“一校一品”特色发展之路。
措施:挖掘当地特色资源,打造特色课程,如农耕文化、民间艺术等,培养学生综合素质。
效果:该校学生在各类比赛中屡获佳绩,教育教学质量稳步提升。
4. 案例四:广东省某中学“研学旅行”实践活动背景:为了拓宽学生的视野,该校开展“研学旅行”实践活动。
措施:组织学生走出校园,参观博物馆、科技馆、红色教育基地等,让学生在实践中学习。
效果:学生的综合素质得到提升,对国家历史、文化有了更深刻的认识。
5. 案例五:湖北省某小学“家校共育”模式探索背景:为了促进学生全面发展,该校积极探索“家校共育”模式。
措施:定期举办家长学校,加强家校沟通,共同关注学生的成长。
效果:学生的家庭教育环境得到改善,家校合作意识明显增强。
6. 案例六:江苏省某中学“德育课程”创新实践背景:为了培养学生的道德素养,该校创新德育课程,将德育融入学科教学。

浙江省教育厅关于印发《浙江省数字教育高质量发展行动计划(2024-2027年)》的通知文章属性•【制定机关】浙江省教育厅•【公布日期】2023.12.27•【字号】浙教技〔2023〕61号•【施行日期】2023.12.27•【效力等级】地方规范性文件•【时效性】现行有效•【主题分类】教育正文浙江省教育厅关于印发《浙江省数字教育高质量发展行动计划(2024-2027年)》的通知浙教技〔2023〕61号各市、县(市、区)教育局,各高等学校:现将《浙江省数字教育高质量发展行动计划(2024—2027年)》印发给你们,请结合实际认真贯彻实施。
附件:《浙江省数字教育高质量发展行动计划(2024—2027年)》浙江省教育厅2023年12月27日附件浙江省数字教育高质量发展行动计划(2024—2027年)为深入贯彻党的二十大关于推进教育数字化的战略部署,加快建设教育强国,深入推进国家教育数字化战略行动,根据《浙江省教育事业发展“十四五”规划》《浙江省教育信息化“十四五”发展计划》等文件精神和浙江省数字教育发展实际,制定本行动计划。
一、总体要求(一)建设目标在高质量发展建设共同富裕示范区背景下,以立德树人为根本任务,坚持“以教育信息化驱动引领教育现代化”的发展理念,充分发挥数字教育推进教育现代化的内变量、快变量、强变量作用,统筹做好技术支撑、数字赋能、应用深化、公共服务、安全保障,构建数字教育基础设施、数字教育资源应用、教育数据开放服务、数字教育协同创新、教育网络安全保障和数字教育发展制度等六大体系完善、结构合理、供给充分的高质量数字教育公共服务体系,支持公平包容、更有质量、适合人人、绿色发展、开放合作的数字教育生态。
到2027年,形成在国内处于领先水平、在国际具有影响力的数字教育高地,助推中国式现代化教育示范省建设。
(二)基本原则立德树人、全面育人。
始终坚持党的全面领导,始终坚持促进人的全面而有个性的发展,为学习者的终身幸福奠基,办好人民满意的教育。

国家中医药管理局关于政协第十三届全国委员会第四次会议第4415号(教育类469号)提案答复的函文章属性•【制定机关】国家中医药管理局•【公布日期】2021.08.24•【文号】国中医药提字〔2021〕51号•【施行日期】2021.08.24•【效力等级】部门规范性文件•【时效性】现行有效•【主题分类】文化正文关于政协第十三届全国委员会第四次会议第4415号(教育类469号)提案答复的函国中医药提字〔2021〕51号高佩璇委员:您提出的《关于推进中医药文化进中小学校园的提案》收悉,现答复如下:党中央、国务院高度重视中医药文化进校园工作,2019年《中共中央国务院关于促进中医药传承创新发展的意见》明确要求,把中医药文化贯穿国民教育始终,中小学进一步丰富中医药文化教育,使中医药成为群众促进健康的文化自觉。
为贯彻落实中央文件精神,推动各地中医药文化进校园工作深入开展,2021年6月,我局联合中央宣传部、教育部、国家卫生健康委、国家广电总局制定印发了《中医药文化传播行动实施方案(2021—2025年)》,将“推动中医药文化贯穿国民教育始终”作为方案重点任务之一予以部署推动。
一、关于研究、设计中医药文化教学内容我局和教育部积极推动将中医药文化纳入中小学课程教学内容。
《义务教育历史课程标准(2011年版)》中,明确要求学生了解三国两晋南北朝时期“中医学已形成系统的理论和独特的治疗方法”“讲述张仲景和华佗的故事”“搜集具体事例,体会中医对我们日常生活的广泛影响”“知道《本草纲目》等名著,了解明代科技的成就及影响”等。
普通高中历史、生物学、体育与健康等学科课程标准(2017年版2020年修订)分别要求学生了解中医药的主要成就,了解李时珍等医药学家的主要事迹以及对社会发展所做的贡献等;知道“植物组织培养在中药材植物等的迅速扩大繁殖等方面发挥了重要的作用”;重视具有中华优秀传统文化特色的养生方法的教学。
除国家课程外,鼓励各地和学校结合实际,挖掘当地资源,开设地方课程、校本课程。

浙江省语言文字工作委员会、浙江省教育厅关于印发《中小学(幼儿园)经典诵读活动指导纲要》的通知文章属性•【制定机关】浙江省语言文字工作委员会,浙江省教育厅•【公布日期】2013.08.20•【字号】浙教语[2013]77号•【施行日期】2013.08.20•【效力等级】地方规范性文件•【时效性】现行有效•【主题分类】教育综合规定正文浙江省语言文字工作委员会、浙江省教育厅关于印发《中小学(幼儿园)经典诵读活动指导纲要》的通知(浙教语〔2013〕77号)各市、县(市、区)语委、教育局,有关高校:为落实《浙江省贯彻〈国家中长期语言文字事业改革和发展规划纲要(2012-2020年)〉的实施意见》,继承与弘扬中华民族优秀文化,促进中小学(幼儿园)全面开展中华经典诵读活动,省语委、省教育厅研究制定了《中小学(幼儿园)中华经典诵读活动指导纲要》(以下简称《指导纲要》),现印发给你们,请于2013年秋季开始执行。
现将有关要求通知如下:一、充分认识开展中华经典诵读活动的重要意义中华经典诗文是中华民族宝贵的文化财富,开展中华经典诵读活动,有助于让学生从经典中体会中国传统文化的家国情怀,汲取民族精神的源头活水,增强民族自信心和自豪感;有助于让学生在熟读成诵的过程中陶冶性情品德,逐步树立社会主义核心价值观,形成自信自强的人格、和善诚信的品质;有助于让学生广泛而深入地撷取国学精华,在记忆的黄金时代增加经典储备,进一步提升文化素养、审美品位及语言文字应用能力。
各地各校要充分认识开展青少年中华经典诵读活动的重要意义,认真学习《指导纲要》,进一步探索中华经典诵读活动的新模式和新途径,促进中小学(幼儿园)全面开展中华经典诵读活动,为全面推进素质教育,建设文化强省、科教人才强省作出积极贡献。
二、加强中华经典诵读活动的指导和管理各级语委、教育行政部门要按照本通知的要求,结合当地实际,制订切实可行的实施方案,力求区域性整体推进中华经典诵读活动。


导游资格习题库(含答案)一、单选题(共44题,每题1分,共44分)1.根据2016年11月30日教育部等11个部门出台的《关于推进中小学生研学旅行的意见》,中小学生研学旅行的主导单位是()。
A、旅行社B、中小学校C、研学基地和营地D、旅游主管部门正确答案:B2.导游人员没有按预定航班(车次、船次)时刻迎接旅游团,导致旅游团到达后无导游人员迎接的现象,称为( )。
A、空接B、错接C、误接D、漏接正确答案:D3.为打造文化特色鲜明的国家级旅游休闲街区,文化和旅游部牵头编制的《旅游休闲街区等级划分》(LB/T082-2021)行业标准,提出旅游休闲街区划分为()个等级。
A、2B、3C、4D、5正确答案:A4.把“玄武门”改为“神武门”,“玄武大帝”改为“真武大帝”是避()皇帝之讳。
A、康熙B、雍正C、乾隆D、道光正确答案:A5.俄罗斯最流行的宗教是()。
A、东正教B、伊斯兰教C、天主教D、萨满教正确答案:A6.个园中的()在扬州古代园林中别具特色,在国内也属罕见。
A、水景B、山水景色C、四季假山D、城市山林正确答案:C7.在下面旅行社四大业务中,属于产品消费的是( )。
A、旅游者接待B、旅游产品销售C、旅游产品开发D、旅游服务采购正确答案:A8.“旅游不文明行为记录”信息保存期限最多为()。
A、3年B、2年C、1年D、5年正确答案:D9.教育部等11部门下发的《关于推进中小学生研学旅行的意见》,明确小学阶段以()研学为主。
A、放眼世界B、县情市情C、省情国情D、乡土乡情正确答案:D10.东大寺是日本佛教()总寺院,距今约有一千二百余年的历史。
A、法相宗B、天台宗C、禅宗D、华严宗正确答案:D11.北京时间为零点时,当地时间为16:00的城市是( )。
A、巴黎B、伦敦C、汉城D、纽约正确答案:B12.为了公共利益的需要,依照法律规定的权限和程序征收、征用不动产或者动产的,应当给予公平、合理的()。
A、赔偿或补偿B、补偿C、赔偿和补偿D、赔偿正确答案:B13.楷书产生于()。

浙江省温州市2019年中考社会法治试卷一、选择题(共20小题,每小题2分,共40分)1.2019年2月,中共中央、国务院印发《________发展规划纲要》。
该纲要的实施,将推动形成全面开放的新格局和“一国两制”事业发展的新实践。
()A. 粤港澳大湾区B. 京津冀地区C. 长江经济带D. 珠三角地区2.为了更好地造福各国人民,第二届________于2019年4月在北京举行。
()A. 二十国集团领导人会议B. 博鳌亚洲论坛C. “一带一路”国际合作高峰论坛D. 中非合作论坛3.看专家建政:在心情沮丧、情绪低落的时候,让自己忙碌起来。
热爱你的工作,让忙碌忘记烦恼。
这说明()A. 转移注意力能调控情绪B. 消除烦恼更有利于工作C. 换位思考可以调节情绪D. 消极情绪也能锻炼意志4.温州爱心市民筹集善款十多万元,帮助西藏嘉黎县两名患病儿童到温州就医并获得康复。
爱心市民的义举主要体现了()A. 懂得保护自己B. 善待他人生命C. 意志需要磨砺D. 履行法律义务5.读下图,回答小题。
(1)对判决书内容解读正确的有()①被告人郑某某侵犯了他人的物质帮助权②多次窃取他人物品具有严重社会危害性③判决的依据是《中华人民共和国刑法》④拘役和罚金既是主刑,又属于附加刑A. ①③B. ①④C. ②③D. ②④(2)从该案件可以看出()①政府应当依法行政②法院应当依法判决③社会应当倡导自由④公民应当遵守法律A. ①③B. ①④C. ②③D. ②④6.下图反映了()①公民行使决定权②人民当家作主的地位③公民享有监督权④人民能直接管理国家A. ①③B. ①④C. ②③D. ②④7.温州某校八(2)班学生开展道德与法治学种社会实践活动(过程如下),受到各方好评。
这一活动告诉我们要()①培养亲社会行为②关心家乡的发展建设③积极参与民主协商④保护青少年合法权益A. ①②B. ①③C. ②④D. ③④8.2019年3月,有报道指出广东作为全国经济最为发达的省份之一,截至2017年底仍有59.5万相对贫困人口未脱贫,贫困发生率1.52%。
2024年春季研学旅行活动方案一、方案背景及目的研学旅行是现代教育实践中的一种重要形式,通过组织学生参与实地考察、体验亲身参与等活动,帮助学生提高综合能力和实践能力。
2024年春季研学旅行活动旨在为学生提供一个多元、开放、综合的学习环境,培养学生的创新意识、实践能力和合作精神。
二、活动内容及安排为了保证活动的多样性和学生的实际需求,本次研学旅行活动将包括以下几个方面的内容:1. 科技创新体验在科技创新体验环节,学生将参观当地知名高科技企业,并进行工厂参观和科技实验。
通过近距离接触创新科技,学生可以更深入地了解科技发展和应用,激发学生的创新意识和实践能力。
2. 自然环境探索在自然环境探索环节,学生将前往当地的自然保护区或自然景观区开展实地考察和生态保护活动。
学生将学习生物多样性保护、生态环境保护等知识,增强学生对环境保护的意识和责任感。
3. 文化遗产传承在文化遗产传承环节,学生将参观当地具有历史、文化价值的遗产建筑、博物馆等场所。
通过了解和学习当地的历史文化,学生可以增强自身的文化自信,培养对传统文化的尊重和理解。
4. 社会实践活动在社会实践环节,学生将参与志愿者活动或社区服务活动,亲身体验社会实践的过程。
通过参与实际社会活动,学生可以感受社会的复杂性和多样性,提高自身的人际交往能力和社会责任感。
三、活动地点及时间安排活动地点:本次研学旅行活动将选择一个有条件和资源丰富的城市作为主要活动地。
在该城市,有着丰富的科技创新企业、自然环境和文化遗产资源,能够满足学生的学习需求。
活动时间:本次研学旅行活动将在2024年春季假期期间进行,为期7天。
具体活动时间安排如下:第一天:抵达目的地,进行活动简介和安全教育培训;第二天:参观科技创新企业,进行工厂参观和科技实验;第三至第五天:前往自然保护区或自然景观区开展实地考察和生态保护活动;第六天:参观文化遗产建筑、博物馆等场所,了解当地的历史文化;第七天:参与志愿者活动或社区服务活动,进行社会实践活动。
嘉兴(舟山)市 2023 年中考试题语文一、社会实践为提升同学们的劳动素养,学校拟开辟校外劳动实践基地,请你参与相关活动。
(16 分)【任务一布置文化墙】1. 为宣传农耕文化,筹备组准备在基地围墙上配上相关图画,请同学们一起参与讨论。
(5 分)组长:我认为可以在墙上画常用农具。
看,这是我画的。
你:好主意!同学们不一定认识这几种农具,我来注一下拼音,再用汉字写出来。
(1)(chú)______头 (2)______ (lián)刀 (3)铁(qiāo)______组长:不错啊!这三个字有不少共同点,你是否也有发现?你:考我?这难不倒我,我可以从造字法、部首等角度去探究发现: (4)2. 筹备组准备在墙上配一副对联。
组长写好了上联“麦浪涌绿波稼穑园前留愿景”,三位组员各自对了下联,请你挑选最合适的一个。
(2 分)A. 犁轻耕沃土古今黎庶乐耕耘B. 田风传野籁桑麻事内话来年C. 农桑扶社稷千载耕耘皆事业【任务二命名种植园】3. 下图是劳动实践基地规划图。
请你从古诗文中寻找灵感,参照 B 园区的命名方式,给 C 或 D 园区命名,并解说你的创意。
(5 分)古诗文提示:《钱塘湖春行》《卜算子· 咏梅》《桃花源记》……◊规划方案:基地分为4 个园区,分别种植粮食作物、蔬菜、树木和花卉。
◊命名解说: B 园区种植蔬菜,取名为“蔬乐园”,创意来源于陶渊明《读<山海经> (其一 )》中的“欢言酌春酒,摘我园中蔬”。
用“蔬乐园”命名,既点明此处种植的是蔬菜,又能体现同学们在劳动实践中体验到的快乐和收获的满足。
【任务三说服好朋友】4. 学校决定让学生参与劳动实践基地的管理。
朋友小舟表示:我们平时学习忙,没有时间;再说也没种植经验,不能参与管理。
请你说服他。
(4 分)..二、文化传承班级开展“文化传千古,非遗焕新彩”探究活动。
请你阅读以下材料,完成相关任务。
(12 分) 前言:非物质文化遗产,是指各种以非物质形态存在的与群众生活密切独家采访:今天,我们为什么要加入非遗名录?让我们来采访一位名录上的“老前辈”,听听它的看法。
浙江省人民政府办公厅关于印发浙江省全民科学素质行动规划纲要实施方案(2021—2025年)的通知文章属性•【制定机关】浙江省人民政府办公厅•【公布日期】2021.12.08•【字号】浙政办发〔2021〕67号•【施行日期】2021.12.08•【效力等级】地方规范性文件•【时效性】现行有效•【主题分类】科学技术综合规定正文浙江省人民政府办公厅关于印发浙江省全民科学素质行动规划纲要实施方案(2021—2025年)的通知浙政办发〔2021〕67号各市、县(市、区)人民政府,省政府直属各单位:《浙江省全民科学素质行动规划纲要实施方案(2021—2025年)》已经省政府同意,现印发给你们,请认真贯彻执行。
浙江省人民政府办公厅2021年12月8日浙江省全民科学素质行动规划纲要实施方案(2021—2025年)根据《国务院关于印发全民科学素质行动规划纲要(2021—2035年)的通知》(国发〔2021〕9号)精神,结合我省实际,制定本实施方案。
一、总体要求以习近平新时代中国特色社会主义思想为指导,全面贯彻落实习近平总书记关于全民科学素质工作重要论述精神,践行社会主义核心价值观、弘扬科学精神,不断提高全民科学素质,为我省高质量发展作出积极贡献。
到2025年,我省公民具备科学素质的比例超过18%,位居全国前列;各区域、各人群科学素质发展不均衡明显改善。
科学素质建设长效协同机制不断完善,“科学普及与科技创新同等重要”的制度安排基本形成。
科学素质建设推动人民精神生活共同富裕,社会文明程度实现新提高。
二、重点任务(一)实施青少年科学素质提升行动。
加强各年龄段青少年科学教育。
将弘扬科学精神和科学家精神贯穿于育人全链条。
完善以学校教育为主阵地的青少年科学教育体系。
加强基础教育阶段探究性教学,保护学生好奇心,培养创新能力。
探索实行科普教育学分制,支持中小学校建设“未来教室”、创新实验室,培育一批富有科技教育特色的幼儿园、中小学校。
浙江省杭州市八区八年级(上)期末语文试卷(含答案)2022-2023学年浙江省杭州市八区八年级(上)期末语文试卷一、文化探源1.(9分)【承先人智慧,张文化自信】请认真阅读上面的文字,完成各小题。
承先人之智慧,张文化之自信。
历史源于一代代人的书写,既有故事,更沉diàn_______出文化、闪耀着智慧。
新时代领路人的“用典”,正是一个感受历史魅力的窗口。
用东汉杨震“四知拒金”说廉洁,引《晏子春秋》“为者常成,行者常至”讲实干……信手拈(A.ni ānB.zhān)来的精妙典故,让新时代领路人的讲话、文章充满魅力、_______,也让人看到历史中yùn_______藏着的智慧与力量。
(1)根据拼音写汉字或给加点字选择正确读音。
①沉diàn___________②yùn___________藏③信手拈(A.niānB.zhān___________来(2)语段中横线上填入成语正确的一项是___________A.扣人心弦B.引人入胜C.心驰神往(3)从下面的两句“习语用典”中选择一句,仿照划线句子的结构续写一个例子。
A.天将降大任于斯人也B.三军可夺帅也,匹夫不可夺志也2.(7分)【诵古代诗文,感文化魅力】在下面文字的画线处,填入古诗名句。
诗词是中国人一直根植在灵魂和血脉深处的文化基因。
当身处喧嚣的闹市,我们不禁向往陶渊明《饮酒(其五)》中“(1),”的悠然自得;当置身广袤的沙漠,我们总会想起唐代诗人王维《使至塞上》中“(2),”的雄浑壮阔;当年老体弱时,我们会用“老骥伏枥;(3),”激励自己要永远乐观奋发,保持思想上的青春;当陷入迷茫时(4)”告诫自己要像松柏一样保持高洁的品性……(5)为了更好地宣传传统文化,同学们特意设计了精美的名言警句书签,请依次将书签空缺处补充完整。
3.(10分)【理教材内容,解红色基因】通过梳理八上语文教材内容,我们发现大量红色文化基因,整理如下:篇目名称文中红色文化基因红色星级《人民解放军百万大军横渡长江》A.毛泽东亲笔撰写的这则消息让我们重温波澜壮阔的解放战争,提醒我们不忘革命先烈,珍惜来之不易的和平。
2023年浙江省丽水市中考数学真题学校:___________姓名:___________班级:___________考号:___________A ....5.在平面直角坐标系中,点()21,1P m -+位于()A .第一象限.第二象限.第三象限6.小霞原有存款52元,小明原有存款70元.从这个月开始,小霞每月存小明每月存12元零花钱,设经过n 个月后小霞的存款超过小明,可列不等式为(A .521570n +>+C .521270n +>+7.如图,在菱形ABCDA .12B .18.如果100N 的压力F 作用于物体上,产生的压强力面积()2S m 的说法正确的是()A .S 小于20.1mB .S 大于0.1m 9.一个球从地面坚直向上弹起时的速度为h (米)适用公式2105h t t =-,那么球弹起后又回到地面所花的时间A .5B .1010.如图,在四边形ABCD 中,AD BC ∥A .2B .22二、填空题11.分解因式:x 2-9=______.12.青田县“稻鱼共生”种养方式因稻鱼双收、互惠共生而受到农户青睐,现有一农户在5块面积相等的稻田里养殖田鱼,产量分别是(单位:kg ):12,13,15,17,18,则这5块稻田的田鱼平均产量是__________kg .13.如图,在ABC 中,AC 的垂直平分线交BC 于点D ,交AC 于点E ,B ADB ∠=∠.若4AB =,则DC 的长是__________.14.小慧同学在学习了九年级上册“4.1比例线段”3节课后,发现学习内容是一个逐步特殊化的过程,请在横线上填写适当的数值,感受这种特殊化的学习过程.图中横线处应填:__________15.古代中国的数学专著《九章算术》中有一题:“今有生丝三十斤,干之,耗三斤十二两.今有干丝一十二斤,问生丝几何?”意思是:“今有生丝30斤,干燥后耗损3斤12两(古代中国1斤等于16两).今有干丝12斤,问原有生丝多少?”则原有生丝为__________斤.16.如图,分别以,,,a b m n 为边长作正方形,已知m n >且满足2am bn -=,4an bm +=.(1)若3,4a b ==,则图1阴影部分的面积是__________;(2)若图1阴影部分的面积为3,图2四边形ABCD 的面积为5,则图2阴影部分的面积是__________.三、解答题20.为全面提升中小学生体质健康水平,我市开展了儿童青少年专家组随机抽取某校各年级部分学生进行了脊柱健康状况筛查.绘制了两幅不完整的统计图表,请根据图表信息解答下列问题:抽取的学生脊柱健康情况统计表类别检查结果人数A正常170B轻度侧弯▲C中度侧弯7D重度侧弯▲(1)求所抽取的学生总人数;(2)该校共有学生1600人,请估算脊柱侧弯程度为中度和重度的总人数;(3)为保护学生脊柱健康,请结合上述统计数据,提出一条合理的建议.21.我市“共富工坊”问海借力,某公司产品销售量得到大幅提升.为促进生产,公司提供了两种付给员工月报酬的方案,如图所示,员工可以任选一种方案与公司签订合同.图解答下列问题:(1)直接写出员工生产多少件产品时,两种方案付给的报酬一样多;(2)求方案二y 关于x 的函数表达式;(3)如果你是劳务服务部门的工作人员,你如何指导员工根据自己的生产能力选择方案.22.某数学兴趣小组活动,准备将一张三角形纸片(如图)进行如下操作,并进行猜想和证明.(1)用三角板分别取,AB AC 的中点,D E ,连接DE ,画AF D E ⊥于点F ;(2)用(1)中所画的三块图形经过旋转或平移拼出一个四边形(无缝隙无重叠),并用三角板画出示意图;(3)请判断(2)中所拼的四边形的形状,并说明理由.23.已知点(),0m -和()3,0m 在二次函数23,(y ax bx a b =++是常数,0)a ≠的图像上.(1)当1m =-时,求a 和b 的值;(2)若二次函数的图像经过点(),3A n 且点A 不在坐标轴上,当21m -<<-时,求n 的取值范围;(3)求证:240b a +=.24.如图,在O 中,AB 是一条不过圆心O 的弦,点,C D 是 AB 的三等分点,直径CE 交AB 于点F ,连结AD 交CF 于点G ,连结AC ,过点C 的切线交BA 的延长线于点H .(1)求证:AD HC ∥;(2)若2OGGC=,求tan FAG ∠的值;(3)连结BC 交AD 于点N ,若O ①若52OF =,求BC 的长;②若10AH =,求ANB 的周长;③若88HF AB ⋅=,求BHC △的面积.参考答案:∵四边形ABCD 是菱形,∴AB CD ∥,AB AD =,AC BD ⊥∵60DAB ∠=︒,且AB AD =,由圆周角定理得:90BDE ∠=︒,45ADB C CBD ∴∠=∠=∠=︒,45ABD DBE EBC ∴∠+∠=︒=∠ABD EBC ∠=∠∴,在ABD △和EBC 中,ADB ABD ∠⎧⎨∠⎩ABD EBC ∴ ,2CE EBAD AB∴==,2212CE AD ∴==⨯=,故选:A .【点睛】本题考查了圆内接四边形、圆周角定理、相似三角形的判定与性质、等腰三角形的性质等知识点,正确判断出点A19.18m【分析】如图:过点D 作DE AB ⊥于点E ,由题意易得4BE CD ==,进而求得7AE =,再通过解直角三角形可得cos 6014AD AE =÷︒=,然后求出AD CD +即可解答.【详解】解:如图:过点D 作DE AB ⊥于点E ,由题意,得4BE CD ==,∵11AB =,∴7AE =.∵60A ∠=︒,∴cos 6014AD AE =÷︒=.∴()18m AD CD +=.即管道A D C --的总长为18m .【点睛】本题主要考查了解直角三角形的应用,理解题意求得cos 6014AD AE =÷︒=是解答本题的关键.20.(1)200人(2)80人(3)答案不唯一,见解析【分析】(1)利用抽取的学生中正常的人数除以对应的百分比即可得到所抽取的学生总人数;(2)用该校学生总数乘以抽取学生中脊柱侧弯程度为中度和重度的百分比即可得到答案;(3)利用图表中的数据提出合理建议即可.【详解】(1)解:17085%200÷=(人).∴所抽取的学生总人数为200人.(2)()1600185%10%80⨯--=(人).∴估算该校学生中脊柱侧弯程度为中度和重度的总人数有80人.(3)该校学生脊柱侧弯人数占比为15%,说明该校学生脊柱侧弯情况较为严重,建议学校要每天组织学生做护脊操等.【点睛】此题考查了统计表和扇形统计图,熟练掌握用部分除以对应的百分比求总数、用样本估计总体是解题的关键.21.(1)30件(2)20600y x =+(3)若每月生产产品件数不足30件,则选择方案二;若每月生产产品件数就是30件,两种方案报酬相同,可以任选一种;若每月生产产品件数超过30件,则选择方案一【分析】(1)由图象的交点坐标即可得到解答;(2)由图象可得点()()0,600,30,1200,设方案二的函数表达式为y kx b =+,利用待定系数法即可得到方案二y 关于x 的函数表达式;(3)利用图象的位置关系,结合交点的横坐标即可得到结论.【详解】(1)解:由图象可知交点坐标为()30,1200,即员工生产30件产品时,两种方案付给的报酬一样多;(2)由图象可得点()()0,600,30,1200,设方案二的函数表达式为y kx b =+,把()()0,600,30,1200代入上式,得600,301200.b k b =⎧⎨+=⎩解得20,600.k b =⎧⎨=⎩∴方案二的函数表达式为20600y x =+.(3)若每月生产产品件数不足30件,则选择方案二;若每月生产产品件数就是30件,两种方案报酬相同,可以任选一种;若每月生产产品件数超过30件,则选择方案一.【点睛】此题考查了从函数图像获取信息、一次函数的应用等知识,从函数图象获取正确信息和掌握待定系数法是解题的关键.22.(1)见解析(2)见解析(3)答案不唯一,见解析【分析】(1)根据题意画出图形即可;(2)方法一:将ADF △绕点D 逆时针旋转180︒到DBM △,将AEF △绕E 点顺时针旋转180︒到CEN 即可得出四边形BCNM ;方法二:将AEF △绕E 点顺时针旋转180︒到CEM ,将ADF △绕点D 逆时针旋转180︒后再沿BC 向右平移到CMN ,即可得出四边形DBCN ;方法三:将ADF △绕点D 逆时针旋转180︒到DBN ,将AEF △绕E 点顺时针旋转180︒后沿CB 向左平移到BNM ,即可得出四边形MBCE ;(3)方法一:先证明点,,,M D E N 在同一直线上,根据DE 为ABC 的中位线,得出DE BC ∥且2BC DE =.证明MN MD DE EN BC =++=且MN BC ∥,得出四边形MBCN 为平行四边形,根据90M ∠=︒,得出平行四边形MBCN 为矩形.方法二:证明点,,,D E M N 在同一直线上,根据DE 为ABC 的中位线,得出DE BC ∥且2BC DE =,证明EN DE =,得出DN BC =且DN BC ∥,证明四边形DBCN 为平行四边形.方法三:证明点,,,M N D E 在同一直线上,根据DE 为ABC 的中位线,得出DE BC ∥且2BC DE =,证明ME BC =且ME BC ∥,得出四边形MBCE 为平行四边形.【详解】(1)解:如图所示:(2)解:方法一:四边形BCNM 为所求作的四边形方法二:四边形DBCN 是所求的四边形.方法三:四边形MBCE 是所求的四边形.(3)解:方法一(图1),∵180,180MDB BDE DEC NEC ∠+∠=︒∠+∠=︒,∴点,,,M D E N 在同一直线上,∵点,D E 分别是,AB AC 的中点,∴DE 为ABC 的中位线,∴DE BC ∥且2BC DE =.∵MD EN DE +=,∴MN MD DE EN BC =++=且MN BC ∥,∴四边形MBCN 为平行四边形.∵AF D E ⊥,90M ∠=︒,∴平行四边形MBCN 为矩形.方法二(图2),∵180,180DEC MEC EMC NMC ∠+∠=︒∠+∠=︒,∴点,,,D E M N 在同一直线上.∵点,D E 分别是,AB AC 的中点,∴DE 为ABC 的中位线,∵180MNB BND ∠+∠=∴点,,,M N D E 在同一直线上.∵点,D E 分别是,AB AC ∴DE 为ABC 的中位线,∴DE BC ∥且2BC DE =∵MD DE =,∴ME BC =且ME BC ∥∴四边形MBCE 为平行四边形.【点睛】本题主要考查了旋转作图或平移作图,平行四边形的判定,矩形的判定,解题的关键熟练掌握旋转的性质和平移的性质.23.(1)1,2a b =-=-(2)42n -<<-(3)见解析【分析】(1)由1m =-(2)先确定函数图像的对称轴为直线结合21m -<<-即可解答;(3)根据图像的对称性得∴BAD CAD ∠=∠.由CE AD ⊥,则AGF AGC ∠=∠又∵AG AG =,∴CAG FAG △≌△,∴CG FG =.设CG a =,则FG a =,∵2OG CG=,∴2,3OG a AO CO a ===.在Rt AOG △中由勾股定理得AO ∴222(3)(2)a AG a =+,∴5AG a =.∴15tan 55FG FAG AG ∠===.(3)①如图1,连结OA ,∵OF∵,AD HC FG GC =∥,∴AH AF =.∵90HCF ∠=︒,∴10AC AH AF ===.设CG x =,则,5FG x OG x ==-由勾股定理得222AG AO OG =-即2225(5)10x x --=-,解得1x =.∴3,6AG AD ==∵ CDDB =,设CG x =,则,5FG x OG x ==-由勾股定理得222AG AO OG =-2222210AF AG FG x x x =+=-+∵,AD HC FG GC =∥,∴12AH AF HF ==,∴12AG HC =.∴111224AF AM HF AB HF ⋅=⋅=∵90,AGF OMF AFG ∠=∠=︒∠∴AFG OFM △∽△,∴AF GF OF FM=,。