MATLAB Simulink中的离散系统模块

第三讲MatlabSimulink ⼊门——离散系统仿真实例第三讲 Matlab/Simulink ⼊门——离散系统仿真实例1、离散系统基本概念1.1 离散系统 离散系统： 是指系统的输⼊和输出仅在离散的时间上取值，⽽且离散的时间具有相同的时间间隔，与连续的概念相反。

设系统输⼊变量为，其中为系统的采样时间，为采样时刻。

由于为⼀固定值，因此系统输⼊，常简记为。

设输出系统为，简记为。

于是，离散系统的数学表达为：1.2线性离散系统 线性离散系统： 是离散系统的⼀种特殊形式，需要同时满⾜(1)、(2)两个条件，即 (1)、齐次性： 对于离散系统，如果对任意的输⼊与给定的常数，下⾯的式⼦总成⽴：则称系统满⾜齐次性。

(2)、叠加性： 对于系统对于输出和，输出分别为 和，总有下⾯的式⼦成⽴：则称系统满⾜叠加性。

对于线性离散系统，其⼀般数学描述为：⽤差分⽅程描述为：状态⽅程：输出⽅程：1.3 Z 变换u (nT ),n =s 0,1,2...T s n T s u (nT )s u (n )y (nT )s y (n )y (n )=f (u (n ),u (n −1),...;y (n −1),y (n −2))T {αu (n )+1βu (n )}=2αT {u (n )}+1βT {u (n )}2y (n )=T {u (n )},n =0,1,2...u (n )αT {αu (n )}=αT {u (n )}u (n )1u (n )2y (n )1y (n )2T {u (n )+1u (n )}=2T {u (n )}+1T {u (n )}2y (n )=f (u (n ),u (n −1),...;y (n −1),y (n −2))x (n +1)=f (x (n ),u (n ),n )y (n )=g (x (n ),u (n ),n ) 变换： 对于⼀个离散信号，其变换为。

⼀般来说离散信号的起始时间往往⼤于零，这时它的变换为，可简记为。

如何在Matlab中进行离散系统设计离散系统设计在工程领域中扮演着重要的角色。

离散系统指的是使用一系列离散时间点进行操作和观测的系统。

而Matlab作为一种强大的数学软件，提供了丰富的工具和函数来进行离散系统设计。

本文将介绍如何使用Matlab进行离散系统设计，并提供一些实际案例来帮助读者理解和应用这些概念。

一、离散系统和离散系统设计概述离散系统是指系统的状态和输出在离散时间点上进行操作和观测，与连续系统相对应。

离散系统设计的目标是通过对系统进行建模、分析和控制，以实现所需的性能指标。

离散系统设计的基本步骤包括系统建模、性能分析和控制器设计。

系统建模是指将实际系统抽象为数学模型，以方便进行分析和设计。

性能分析是评估系统在不同工况下的性能表现，如稳定性、响应速度等。

控制器设计是根据性能要求设计出合适的控制器，使得系统能够满足需求。

二、Matlab中的离散系统建模在Matlab中，可以使用多种方法进行离散系统的建模。

最常用的方法是差分方程法和状态空间法。

差分方程法是将系统的输入输出关系表示为差分方程的形式，而状态空间法则是使用状态向量和状态方程来描述系统的动态行为。

在使用差分方程法进行建模时，可以使用Matlab中的函数tf或zpk来创建传递函数模型。

传递函数模型是用来描述系统输入和输出之间的关系的一种数学表达式。

例如，通过以下代码可以创建一个二阶传递函数模型：```matlabnum = [1, 0.5];den = [1, -0.6, 0.08];sys = tf(num, den, 1);```在使用状态空间法进行建模时，可以使用Matlab中的函数ss来创建状态空间模型。

状态空间模型是使用状态向量和状态方程来描述系统的动态行为的一种数学表达式。

例如，通过以下代码可以创建一个二阶状态空间模型：```matlabA = [0, 1; -0.08, 0.6];B = [0; 1];C = [1, 0.5];D = 0;sys = ss(A, B, C, D, 1);```三、离散系统性能分析离散系统的性能分析是评估系统在不同工况下的性能表现，如稳定性、响应速度等。

Simulink中连续与离散模型的区别matlab/simulink/simpowersystem中连续vs离散!本文中的一些具体数学推导见下面：计算机仿真技术1.连续系统vs离散系统连续系统是指系统状态的改变在时间上是连续的，从数学建模的角度来看，可以分为连续时间模型、离散时间模型、混合时间模型。

其实在simpowersystem的库中基本所有模型都属于连续系统，因为其对应的物理世界一般是电机、电源、电力电子器件等等。

离散系统是指系统状态的改变只发生在某些时间点上，而且往往是随机的，比如说某一路口一天的人流量，对离散模型的计算机仿真没有实际意义，只有统计学上的意义，所以在simpowersystem中是没有模型属于离散系统的。

但是在选取模型，以及仿真算法的选择时，常常提到的discrete model、discrete solver、discrete simulate type等等中的离散到底是指什么呢？其实它是指时间上的离散，也就是指离散时间模型。

下文中提到的连续就是指时间上的连续，连续模型就是指连续时间模型。

离散就是指时间上的离散，离散模型就是指离散时间模型，而在物理世界中他们都同属于连续系统。

为什么要将一个连续模型离散化呢？主要是是从系统的数学模型来考虑的，前者是用微分方程来建模的，而后者是用差分方程来建模的，并且差分方程更适合计算机计算，并且前者的仿真算法（simulationsolver）用的是数值积分的方法，而后者则是采用差分方程的状态更新离散算法。

在simpowersystem库中，对某些物理器件，既给出的它的连续模型，也给出了它的离散模型，例如：离散模型一个很重要的参数就是采样时间sampletime，如何从数学建模的角度将一个连续模型离散化，后面会有介绍。

在simpowersystem中常用powergui这个工具来将系统中的连续模型离散以便采用discrete算法便于计算机计算。

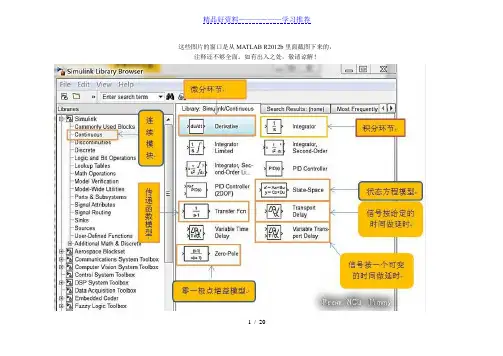
精品好资料——————学习推荐这些图片的窗口是从MA TLAB R2012b里面截图下来的，注释还不够全面。

如有出入之处，敬请谅解！1/ 20Derivative ：微分模块，输出为输入信号的微分。

无需设置参数Integrator：积分模块，输出时输入信号的积分，可设定初始条件（比如混沌系统的仿真），通常情况下初始条件不用考虑Memory：输出来自前一个时间步的模块输入State-Space：状态空间模块，主要应用应用于现代控制理论中多输入多输出系统的仿真，双击模块可设置的主要参数有：系数矩阵A,B,C,D以及初始条件Transfer Fcn：传递函数多项式模型，实现现行传递系统，双击可设置分子多项式和坟墓多项式的系数Transport Delay：时间延迟模块，通过模块内部参数设定延迟时间Variable Transport Delay：将输入延迟一可变的时间Zero-Pole：传递函数零、极点模型，实现一个用零极点标明的传递函数，双击设置零点、极点、增益2/ 20Backlash：磁滞回环特性模块Coulomb & Viscous Friction：库伦摩擦与黏性摩擦特性模块Dead Zone：死区特性模块Hit Crossing：检测输入信号的零交叉点模块Quantizer：阶梯状量化处理模块Rate Limiter：变化速率限幅模块Relay：带有滞环的继电特性模块Saturation：限幅的饱和特性模块3/ 204/ 20Discrete Transfer Fcn：离散系统传递函数多项式模型，可设置分子分母多项式Discrete Zero-Pole：离散系统传递函数零极点模型，可设置零点、极点、增益，可以设置采样时间Discrete Filter：离散系统滤波器，可设置分子分母系数（按照z-1作升幂排列），可设置采样时间Discrete State-Space：离散系统状态空间表达式模块，可设置参数矩阵A,B,C,D，可设置采样时间、初始条件Discrete-Time Integrator：离散系统积分器模块，可设置采样时间、初始条件Unit Delay：离散系统单位延迟模块，可设置采样时间，初始条件Fist-Order Hol：一阶采样保持器Memory：存储模块Zero-Order Hold：零阶采样保持器Discrete Filter：实现IIR和FIR滤波器Discrete State-Space：实现一个离散状态空间系统Discrete-Time Integrator：离散时间积分器Discrete Transfer Fcn ：实现一个离散传递函数Discrete Zero-Pol：实现一个用零极点来说明的离散传递函数First-Order Hold：实现一个一阶保持采样-保持系统Unit Delay：将信号延时一个单位采样时间Zero-Order Hold：实现具有一个采样周期的零阶保持5/ 206/ 20Direct Look-Up Table（n-D）：直接查询n维表模块Interpolation（n-D）Using Prelook-up：适用预查询的n维内查表模块Look-Up Table：一维查表模块Look-Up Table（2-D）：二维查表模块Look-Up Table（n-D）：n维查表模块Prelook-Up Index Search：预查询索引搜寻模块7/ 208/ 20Abs：绝对值或复数求模模块，输出是输入信号的绝对值（或复数的模）Algebraic Constraint：代数约束模块，将输入信号约束为零，计算输入信号为零时的状态值Assignment：分配器模块Bitwise Logical Operator：位逻辑运算模块，可选择逻辑运算关系（与-AND，或-OR，非-NOT，异或-XOR等），可设置第二运算数（默认值为FFFF）Combinatorial Logic：实现一个真值表，组合逻辑运算模块Complex to Magnitude-Angle：复数模、角运算模块，输入量为复数，输出量有两个，一个输出为输入信号的模，另一个为输入信号的角Complex to Real-Imag：复数实部、虚部运算模块，输入量为复数，输出量有两个，一个输出为输入信号的实部，另一个为输入信号的虚部Derivative：输出输入信号的时间微分Dot Product：两输入信号进行点积（内积）运算，无需设置参数Gain：增益模块，将模块的输入信号乘上一个增益Logical Operator：多输入单输出逻辑运算模块，可选择逻辑运算关系（与-AND，或-OR，非-NOT，异或-XOR等）、设置输入信号的个数Magnitude-Angle to Complex：模角生成复数模块，默认输入量有两个：一模一角。

simulink离散仿真简单实例Simulink是MATLAB的一个工具箱，它提供了一个图形化界面，用于建立和模拟动态系统。

它使用块图的形式表示系统，其中每个块代表系统中的一个组件或功能单元。

这些块可以通过线连接在一起，以表示信号的流动。

通过配置块的参数和连接，可以建立一个完整的系统模型。

在Simulink中进行离散仿真时，时间被划分为离散的步长，系统在每个步长内的行为被模拟。

离散仿真可以用于分析系统在不同时间点的行为，例如系统的稳定性、响应时间等。

接下来，我们将通过一个简单的实例来展示Simulink离散仿真的过程。

假设我们要建立一个简单的温度控制系统，系统包括一个温度传感器、一个控制器和一个加热器。

温度传感器用于测量当前环境温度，控制器根据测量值调整加热器的功率。

在Simulink中创建一个新的模型。

在模型中，我们将使用三个块来表示系统的各个组件：一个输入块用于表示环境温度的输入信号，一个控制器块用于调整加热器的功率，一个输出块用于表示系统的输出信号。

接下来，我们需要配置每个块的参数和连接它们。

输入块可以配置为生成一个随机的环境温度信号，控制器块可以配置为根据测量值输出一个控制信号，输出块可以配置为显示系统的输出信号。

通过连接输入块、控制器块和输出块，我们可以建立一个完整的系统模型。

在配置完模型后，我们可以设置仿真参数。

例如，我们可以设置仿真的时间范围、步长等参数。

然后，我们可以运行仿真并观察系统的行为。

通过仿真结果，我们可以分析系统的稳定性、响应时间等性能指标。

通过这个简单的实例，我们可以看到Simulink离散仿真的基本过程。

首先，我们建立一个系统模型，然后配置各个组件的参数和连接它们。

最后，我们设置仿真参数并运行仿真来分析系统的行为。

Simulink离散仿真可以应用于各种实际问题的建模和分析。

例如，它可以用于分析控制系统的性能、优化电路设计、评估通信系统的可靠性等。

通过Simulink离散仿真，我们可以更好地理解和改善系统的行为。

SIMULINK的模块库介绍SIMILINK模块库按功能进行分为以下8类子库：Continuous（连续模块）Discrete（离散模块）Function&Tables（函数和平台模块）Math（数学模块）Nonlinear（非线性模块）Signals&Systems（信号和系统模块）Sinks（接收器模块）Sources（输入源模块）连续模块（Continuous）continuous.mdlIntegrator：输入信号积分Derivative：输入信号微分State-Space：线性状态空间系统模型Transfer-Fcn：线性传递函数模型Zero-Pole：以零极点表示的传递函数模型Memory：存储上一时刻的状态值Transport Delay：输入信号延时一个固定时间再输出Variable Transport Delay：输入信号延时一个可变时间再输出离散模块（Discrete）discrete.mdlDiscrete-time Integrator：离散时间积分器Discrete Filter：IIR与FIR滤波器Discrete State-Space：离散状态空间系统模型Discrete Transfer-Fcn：离散传递函数模型Discrete Zero-Pole：以零极点表示的离散传递函数模型First-Order Hold：一阶采样和保持器Zero-Order Hold：零阶采样和保持器Unit Delay：一个采样周期的延时函数和平台模块(Function&Tables) function.mdlFcn：用自定义的函数（表达式）进行运算MATLAB Fcn：利用matlab的现有函数进行运算S-Function：调用自编的S函数的程序进行运算Look-Up Table：建立输入信号的查询表（线性峰值匹配）Look-Up Table(2-D)：建立两个输入信号的查询表（线性峰值匹配）数学模块（Math ）math.mdlSum：加减运算Product：乘运算Dot Product：点乘运算Gain：比例运算Math Function：包括指数函数、对数函数、求平方、开根号等常用数学函数Trigonometric Function：三角函数，包括正弦、余弦、正切等MinMax：最值运算Abs：取绝对值Sign：符号函数Logical Operator：逻辑运算Relational Operator：关系运算Complex to Magnitude-Angle：由复数输入转为幅值和相角输出Magnitude-Angle to Complex：由幅值和相角输入合成复数输出Complex to Real-Imag：由复数输入转为实部和虚部输出Real-Imag to Complex：由实部和虚部输入合成复数输出非线性模块（Nonlinear ）nonlinear.mdlSaturation：饱和输出，让输出超过某一值时能够饱和。

Simulink 中的模块一：连续模块库(Continuous)1.积分模块(Integrator)：功能：对输入变量进行积分。

说明：模块的输入可以是标量，也可以是矢量；输入信号的维数必须与输入信号保持一致。

2. 微分模块(Derivative)功能：通过计算差分A u/A t 近似计算输入变量的微分。

功能：用于建立一个预先指定的零点、极点，并用延迟算子s 表示的连续。

7.传输延迟模块(TransportDelay) 功能：用于将输入端的信号延迟指定的时间后再传输给输出信号8. 可变传输延迟模块(VariableTransportDelay) 功能：用于将输入端的信号进行可变时间的延迟。

二：离散模块库(Discrete)1 •零阶保持器模块(Zero-Order-Hold)功能：在一个步长内将输出的值保持在同一个值上。

2 .单位延迟模块(UnitDelay)功能：将输入信号作单位延迟，并且保持一个采样周期相当于时间算子z -1。

3•离散时间积分模块(DiscreteTimeIntegrator)功能：在构造完全离散的系统时，代替连续积分的功能。

使用的积分方法有：向前欧拉法向后欧拉法、梯形法。

6•离散传递函数模块(DiscreteTransferFcn)3. 线性状态空间模块(State-Space) 功能：用于实现以下数学方程描述的系统4. 传递函数模块(TransferFen) 功能：用执行一个线性传递函数。

5. 零极点传递函数模块(Zero-Pole)Ax y =Cx +Bu +Du4 •离散状态空间模块(DiscreteStateSpace)'功能：用于实现如下数学方程描述的系统：＜5 •离散滤波器模块(DiscreteFilter) x[(n +1)T]=Ax(nT)+Bu(nT) 功能：用于实现无限脉冲响应(IIR )和有限脉冲响应T R)的数C 滤波器。

)+Du (nT )功能：用于执行一个离散传递函数。

学生实验报告图18-9四、实验结论与心得永磁交流伺服电机位置反馈传感器检测相位与电机磁极相位的对齐方式2008-11-07 来源：internet 浏览：504主流的伺服电机位置反馈元件包括增量式编码器，绝对式编码器，正余弦编码器，旋转变压器等。

为支持永磁交流伺服驱动的矢量控制，这些位置反馈元件就必须能够为伺服驱动器提供永磁交流伺服电机的永磁体磁极相位，或曰电机电角度信息，为此当位置反馈元件与电机完成定位安装时，就有必要调整好位置反馈元件的角度检测相位与电机电角度相位之间的相互关系，这种调整可以称作电角度相位初始化，也可以称作编码器零位调整或对齐。

下面列出了采用增量式编码器，绝对式编码器，正余弦编码器，旋转变压器等位置反馈元件的永磁交流伺服电机的传感器检测相位与电机电角度相位的对齐方式。

增量式编码器的相位对齐方式在此讨论中，增量式编码器的输出信号为方波信号，又可以分为带换相信号的增量式编码器和普通的增量式编码器，普通的增量式编码器具备两相正交方波脉冲输出信号A和B，以及零位信号Z；带换相信号的增量式编码器除具备ABZ 输出信号外，还具备互差120度的电子换相信号UVW，UVW各自的每转周期数与电机转子的磁极对数一致。

带换相信号的增量式编码器的UVW电子换相信号的相位与转子磁极相位，或曰电角度相位之间的对齐方法如下：1.用一个直流电源给电机的UV绕组通以小于额定电流的直流电，U入，V 出，将电机轴定向至一个平衡位置；2.用示波器观察编码器的U相信号和Z信号；3.调整编码器转轴与电机轴的相对位置；4.一边调整，一边观察编码器U相信号跳变沿，和Z信号，直到Z信号稳定在高电平上（在此默认Z信号的常态为低电平），锁定编码器与电机的相对位置关系；5.来回扭转电机轴，撒手后，若电机轴每次自由回复到平衡位置时，Z信号都能稳定在高电平上，则对齐有效。

撤掉直流电源后，验证如下：1.用示波器观察编码器的U相信号和电机的UV线反电势波形；2.转动电机轴，编码器的U相信号上升沿与电机的UV线反电势波形由低到高的过零点重合，编码器的Z信号也出现在这个过零点上。

色子科技大学学院学生卖验报告院别：电子传息学院课程名称：传号与糸统实验-、卖验目的1. 拿握富散糸统Simulink的建栈方冻。

2. 拿墟禽散糸统肘城响应、频城响应的Simulink仿真方出。

二、卖验原理富散糸统的Simulink建模、仿真方比匀连续糸统相似，其糸统橈型主要有z 城核型、传输函数栈空和状态咗间栈型等形无。

现采用图1的形无建立糸统仿真栈型，结合如下仿真的令令，可得到糸统的状态咗间变量、频率响应曲线J、单住阶趾响应和单伐冲激响应的沐形。

图1糸统响应Simulink仿真的综合棋型仿真令令：[ABC、叨二dlinmodC'棋型丈件名'丿％求状态空间矩阵，注意：'模黑丈件名不含护展名dimpulse(A,B,C,D) %求冲激响应dimpuke(A,B,C,D」,N]：N J %求k=N[~ N, £间(步长为U的冲激响应dimpulse（ABC,DJ,N]:△“：N2）%求冲激响应Ak=N[~ N2 g.间（步长NJ的部分祥■值dstep（A.BCD） %求阶跃响应dstep（A、BCD、1,N ] :Z\N:N Jdbode（A.B,C,D.T c）%求频率响应（频：“ = 0~上_,印0 = 0~兀丿。

为Ts取挥周期.一般去T$=1・dbode（A,B,C,D. T y ,i d ,w0: Aw:wJ % 求频率响应（频4 = ® ： 0 =w° ~ w「即&= （w（）~ W]丿T「Aw为频率步长丿；i“为糸疣输入夠D的偏号，糸统只冇一个输入端o肘取i“ =1.以上令令，可以逐条症MATLAB令令窗d输入.执行"也可偏写成M丈件并运行。

三、实验彖1.^＜糸统肘城柩图如国2所示。

建立Simulink核型，求其状态吨间矩阵.糸统函数.冲激响应.阶跃响应和频率特性。

3.^ ＜糸统差分方程为y伙）+ - y（k一1）一丄y（k一2） = /伙）+ 2 f（k一2）。

simulink的离散系统微分模块
在Simulink中，离散系统微分模块可以通过Discrete-Time Integrator模块来实现。

该模块可以执行类似于连续时间微分器的操作，但是是在离散时间步长上执行的。

在Simulink中，可以使用如下步骤创建离散系统微分模块：
1. 打开Simulink并创建一个新模型；
2. 从Simulink库中拖动Discrete-Time Integrator模块并放置到
模型中；
3. 配置Discrete-Time Integrator模块的参数，如初始值、采样时间、积分限制等；
4. 连接Discrete-Time Integrator模块的输入信号和输出信号；
5.运行模型来模拟离散系统微分模块的行为。

例如，下面是一个使用Discrete-Time Integrator模块实现离散系
统微分的示例模型：
。

在该模型中，Discrete-Time Integrator模块的初始值为0，采样时
间为0.01秒，上限和下限都为无穷大。

输入信号为单位阶跃信号，输出
信号为阶跃信号在每个离散时间步长上的增量。

运行该模型可以得到如下结果：
。

可以看到，离散系统微分模块的输出信号等效于输入信号在每个离散时间步长上的增量，即数值微分结果。

simulink离散传递函数模块
Simulink中的离散传递函数模块可以用于对离散时间信号进行
离散时间域的传递函数处理。

在Simulink中，离散传递函数模块可以通过以下步骤进行设置：
1. 打开Simulink模型并找到离散传递函数模块。

2. 双击该模块以打开模块对话框。

3. 在模块对话框中，输入传递函数的离散时间域表达式。

表达式应包括多项式的系数，如：
y(n) = b0 x(n) + b1 x(n-1) + b2 x(n-2) - a1 y(n-1) - a2 y(n-2)
其中b0、b1、b2、a1、a2分别为多项式系数，x(n)和y(n)分
别为输入和输出离散时间信号。

4. 根据需要设置其他模块参数，如采样时间、模块输入和输出端口等。

5. 保存模型并运行仿真以测试模块的功能。

通过使用离散传递函数模块，可以实现对离散时间信号的滤波、增益控制和延迟等基本处理。

simulink的离散积分模块的accumulation
Simulink是MATLAB的一个扩展包，主要用于进行系统模拟和分析。

在Simulink 中，离散积分模块通常用于对离散时间信号进行积分操作。

关于离散积分模块的累积（accumulation），这涉及到在给定的离散时间点上对信号的累积效应进行建模。

具体来说，离散积分模块通过将每个时间步长的输入值累加到上一个时间步长的累积值上来工作。

这种累积行为对于模拟诸如存储器、电荷、质量等物理系统的行为特别有用。

例如，考虑一个简单的离散积分模块，其数学表示为：
(y[n] = y[n-1] + x[n] \cdot T)
其中：
•(y[n]) 是当前时间步长的输出。

•(y[n-1]) 是上一个时间步长的输出累积值。

•(x[n]) 是当前时间步长的输入。

•(T) 是时间步长。

通过将每个时间步长的输入与上一个时间步长的输出累积起来，离散积分模块可以模拟连续时间的积分行为。

在Simulink中，你可以通过调整模块参数来改变累积分隔、初始条件等，以适应不同的应用需求。

Matlab中SIMULINK的模块库以及比较常用的模块2009年04月18日星期六 13:41SIMULINK的模块库介绍SIMILINK模块库按功能进行分为以下8类子库：Continuous（连续模块）Discrete（离散模块）Function&Tables（函数和平台模块）Math（数学模块）Nonlinear（非线性模块）Signals&Systems（信号和系统模块）Sinks（接收器模块）Sources（输入源模块）连续模块（Continuous）continuous.mdlIntegrator：输入信号积分Derivative：输入信号微分State-Space：线性状态空间系统模型Transfer-Fcn：线性传递函数模型Zero-Pole：以零极点表示的传递函数模型Memory：存储上一时刻的状态值Transport Delay：输入信号延时一个固定时间再输出Variable Transport Delay：输入信号延时一个可变时间再输出离散模块（Discrete） discrete.mdlDiscrete-time Integrator：离散时间积分器Discrete Filter：IIR与FIR滤波器Discrete State-Space：离散状态空间系统模型Discrete Transfer-Fcn：离散传递函数模型Discrete Zero-Pole：以零极点表示的离散传递函数模型First-Order Hold：一阶采样和保持器Zero-Order Hold：零阶采样和保持器Unit Delay：一个采样周期的延时函数和平台模块(Function&Tables) function.mdlFcn：用自定义的函数（表达式）进行运算MATLAB Fcn：利用matlab的现有函数进行运算S-Function：调用自编的S函数的程序进行运算Look-Up Table：建立输入信号的查询表（线性峰值匹配）Look-Up Table(2-D)：建立两个输入信号的查询表（线性峰值匹配）数学模块（ Math ） math.mdlSum：加减运算Product：乘运算Dot Product：点乘运算Gain：比例运算Math Function：包括指数函数、对数函数、求平方、开根号等常用数学函数Trigonometric Function：三角函数，包括正弦、余弦、正切等MinMax：最值运算Abs：取绝对值Sign：符号函数Logical Operator：逻辑运算Relational Operator：关系运算Complex to Magnitude-Angle：由复数输入转为幅值和相角输出Magnitude-Angle to Complex：由幅值和相角输入合成复数输出Complex to Real-Imag：由复数输入转为实部和虚部输出Real-Imag to Complex：由实部和虚部输入合成复数输出非线性模块（ Nonlinear ） nonlinear.mdlSaturation：饱和输出，让输出超过某一值时能够饱和。

在 MATLAB Simulink 中，Discrete-Time Integrator 模块用于进行离散时间积分操作。

该模块可以在 Simulink 模型中创建一个离散时间积分器，用于对输入信号进行累
积求和。

初始条件是在模块初始化时给定的初始积分值。

Discrete-Time Integrator 模块的基本参数：
1.Initial condition (初始条件)：
▪初始条件表示在模块开始运行时的初始积分值。

可以在模块的参数中设置这个初始条件。

MATLAB 指令示例：
在 Simulink 模型中，通过在模型中添加 Discrete-Time Integrator 模块，并设置初始
条件，可以实现对输入信号的离散时间积分。

以下是 MATLAB 指令的示例：
在上述示例中，InitialCondition参数被设置为initialCondition的值。

这个值可以根据你
的需求设置为任何你希望的初始积分值。

请注意，这只是一个简单的示例，实际使用中需要根据具体的系统和控制需求来设置初始条件和其他参数。