专题：波的多解问题

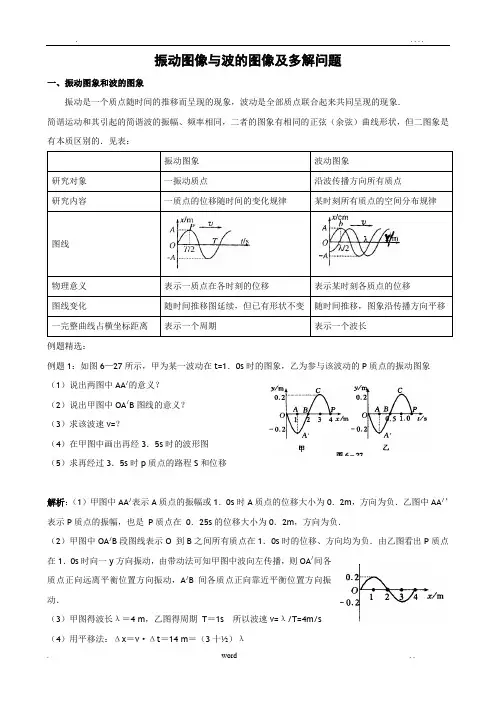
振动图像与波的图像及多解问题一、振动图象和波的图象振动是一个质点随时间的推移而呈现的现象，波动是全部质点联合起来共同呈现的现象．简谐运动和其引起的简谐波的振幅、频率相同，二者的图象有相同的正弦（余弦）曲线形状，但二图象是有本质区别的．见表：振动图象波动图象研究对象一振动质点沿波传播方向所有质点研究内容一质点的位移随时间的变化规律某时刻所有质点的空间分布规律图线物理意义表示一质点在各时刻的位移表示某时刻各质点的位移图线变化随时间推移图延续，但已有形状不变随时间推移，图象沿传播方向平移一完整曲线占横坐标距离表示一个周期表示一个波长例题精选：例题1：如图6—27所示，甲为某一波动在t=1．0s时的图象，乙为参与该波动的P质点的振动图象（1）说出两图中AA/的意义？（2）说出甲图中OA/B图线的意义？（3）求该波速v=？（4）在甲图中画出再经3．5s时的波形图（5）求再经过3．5s时p质点的路程S和位移解析：（1）甲图中AA/表示A质点的振幅或1．0s时A质点的位移大小为0．2m，方向为负．乙图中AA/’表示P质点的振幅，也是P质点在0．25s的位移大小为0．2m，方向为负．（2）甲图中OA/B段图线表示O 到B之间所有质点在1．0s时的位移、方向均为负．由乙图看出P质点在1．0s时向一y方向振动，由带动法可知甲图中波向左传播，则OA/间各质点正向远离平衡位置方向振动，A/B间各质点正向靠近平衡位置方向振动．（3）甲图得波长λ＝4 m，乙图得周期T＝1s 所以波速v=λ/T=4m/s（4）用平移法：Δx＝v·Δt＝14 m＝（3十½）λ所以只需将波形向x 轴负向平移½λ=2m 即可，如图6——28所示 （5）求路程：因为n=2/T t=7，所以路程S=2An=2×0·2×7=2。

8m求位移：由于波动的重复性，经历时间为周期的整数倍时．位移不变·所以只需考查从图示时刻，p 质点经T/2时的位移即可，所以经3．5s 质点P 的位移仍为零．例题2：如图所示，（1）为某一波在t ＝0时刻的波形图，（2）为参与该波动的P 点的振动图象，则下列判断正确的是A ． 该列波的波速度为4m ／s ；B ．若P 点的坐标为x p ＝2m ，则该列波沿x 轴正方向传播C ．该列波的频率可能为 2 Hz ；D ．若P 点的坐标为x p ＝4 m ，则该列波沿x 轴负方向传播；解析：由波动图象和振动图象可知该列波的波长λ=4m ，周期T ＝1．0s ，所以波速v ＝λ／T ＝4m ／s ． 由P 质点的振动图象说明在t=0后，P 点是沿y 轴的负方向运动：若P 点的坐标为x p ＝2m ，则说明波是沿x 轴负方向传播的；若P 点的坐标为x p ＝4 m ，则说明波是沿x 轴的正方向传播的．该列波周期由质点的振动图象被唯一地确定，频率也就唯一地被确定为f ＝ l ／t ＝0Hz ．综上所述，只有A 选项正确．点评：当一列波某一时刻的波动图象已知时，它的波长和振幅就被唯一地确定，当其媒质中某质点的振动图象已知时，这列波的周期也就被唯一地确定，所以本题中的波长λ、周期T 、波速v 均是唯一的．由于质点P 的坐标位置没有唯一地确定，所以由其振动图象可知P 点在t ＝0后的运动方向，再由波动图象确定波的传播方向二、波动图象的多解波动图象的多解涉及：(1)波的空间的周期性；(2)波的时间的周期性；(3)波的双向性；(4)介质中两质点间距离与波长关系未定；(5)介质中质点的振动方向未定． 1．波的空间的周期性沿波的传播方向，在x 轴上任取一点P （x)，如图所示，P 点的振动完全重复波源O 的振动，只是时间上比O 点要落后Δt ，且Δt =x/v=xT 0/λ.在同一波线上，凡坐标与P 点坐标x 之差为波长整数倍的许多质点，在同一时刻t 的位移都与坐标为λ的质点的振动位移相同，其振动速度、加速度也与之相同，或者说它们的振动“相貌”完全相同．因此，在同一波线上，某一振动“相貌”势必会不断重复出现，这就是机械波的空间的周期性．空间周期性说明，相距为波长整数倍的多个质点振动情况完全相同． 2．波的时间的周期性在x 轴上同一个给定的质点，在t+nT 时刻的振动情况与它在t 时刻的振动情况（位移、速度、加速度等）相同．因此，在t 时刻的波形，在t+nT 时刻会多次重复出现．这就是机械波的时间的周期性． 波的时间的周期性，表明波在传播过程中，经过整数倍周期时，其波的图象相同． ①传播距离：x n x ∆+=λ0 ②传播时间：t nT t ∆+= ③传播速度：t nT x n t x v ∆+∆+==λ0④质点振动路程：s nA s ∆+=4 3．波的双向性双向性是指波沿正负方向传播时，若正、负两方向的传播时间之和等于周期的整数倍，则沿正负两方向传播的某一时刻波形相同．4．介质中两质点间的距离与波长关系未定在波的传播方向上，如果两个质点间的距离不确定，就会形成多解，解题时若不能联想到所有可能情况，易出现漏解．5．介质中质点的振动方向未定在波的传播过程中，质点振动方向与传播方向联系，若某一质点振动方向未确定，则波的传播方向有两种，这样形成多解．说明：波的对称性：波源的振动要带动它左、右相邻介质点的振动，波要向左、右两方向传播．对称性是指波在介质中左、右同时传播时，关于波源对称的左、右两质点振动情况完全相同．5．已知波速v 和波形，画出再经t ∆时间波形图的方法⑴平移法：先算出经t ∆时间波传播的距离t v x ∆⋅=∆，再把波形沿波的传播方向平移x ∆即可。

专题十五 机械振动和机械波必刷62波的多解问题1．（2020·银川·宁夏大学附属中学月考）一列简谐横波沿直线传播，某时刻该列波上正好经过平衡位置的两质点相距6m ，且这两质点之间的波峰只有一个，则该简谐波可能的波长为（ ） A ．4m 、6m 和12m B ．6m 、8m 和12m C ．4m 、8m 和14mD ．8m 、12m 和14m2．（2020·山东罗庄·临沂十八中高二月考）一列简谐横波沿x 轴正方向传播，t 时刻波形图如图实线所示，此时波刚好传到P 点，0.6s t +时刻的波形如图中虚线所示，a 、b 、c 、P 、Q 是介质中的质点，则下列说法正确的是（ ）A ．这列波的波速一定是50m /sB ．质点a 在这段时间内通过的路程一定小于30cmC ．若周期0.8s T =，则在0.8s t +时刻，质点Q 速度最大D ．质点c 在这段时间内通过的路程可能为60cm3．（2020·三明市第二中学高二月考）如图所示为一列沿x 轴正方向传播的简谐横波，实线为10t =时刻的波形图，虚线为20.2s t =时的波形图。

则（ ）A ．N 、Q 两质点的振动情况总是相同的B ．这列波的波速可能为24m /s v =C ．10t =时刻的波形图上的M 点经0.5s 可能达到Q 点D ．从2t 时刻起再经过0.7s t ∆=质点M 可能处于波峰位置4．（2020·天津高三二模）有一列沿水平绳向右传播的简谐横波，频率为10Hz ，振动方向沿竖直方向。

当绳上的质点P 到达其平衡位置且向下运动时，在其平衡位置右方相距0.9m 处的质点Q 刚好到达最高点，由此可知波速不可能的是（ ） A ．36m/sB ．4m/sC ．7.2m/sD ．12m/s5．（2020·山东高二学业考试）如图，一列简谐横波沿x 轴正方向传播，a 、b 是x 轴上离坐标原点由近及远的两质点，图甲和图乙分别为x 轴上a 、b 两质点的振动图像，且x ab 为6m 。

小专题研究(三) 波的多解问题1．方向性不确定出现多解波总是由波源发出并由近及远地向前传播，波在介质中传播时，介质各质点的振动情况根据波的传播方向是可以确定的，反之亦然。

因此，根据题中的已知条件不能确定波的传播方向或者不能确定质点的振动方向，就会出现多解，然而同学们在解题中往往凭着主观臆断，先入为主地选定某一方向为波的传播方向或是质点的振动方向，这样就会漏掉一个相反方向的可能性解。

2．时间、距离不确定形成多解沿着波的传播方向，相隔一个波长的连续两个相邻的质点振动的步调是完全相同的；在时间上相隔一定周期的前后两个相邻时刻的波形图线是完全相同的，所以，当题中已知条件没有给定传播的时间(波传播的时间Δt 与周期T 之间的大小关系不确定)或是没有给定波的传播距离(波的传播距离Δs 与波长λ之间的大小关系不确定)，就会出现多解现象。

同学们在解题时经常只分析传播时间Δt 小于T (或传播距离Δs 小于波长λ)的特解情况，从而造成特解代替通解的漏解现象。

3．两质点间关系不确定形成多解在波的传播方向上，如果两质点间距离不确定或相位之间关系不确定，会形成多解，若不会联想所有的可能性，就会出现漏解。

[例证] 一列简谐横波沿直线传播，在传播方向上有P 、Q 两个质点，它们相距8 m ，当t ＝0时，P 、Q 的位移恰好是正最大值，且P 、Q 之间只有一个波谷。

t ＝0.6 s 末时，P 、Q 两点正好都处在平衡位置，且P 、Q 之间只有一个波峰和一个波谷，且波峰距Q 点的距离第一次为λ4，试求：(1)波由P 传至Q ，波的周期； (2)波由Q 传到P ，波的速度；(3)波由Q 传到P ，从t ＝0时开始观察，哪些时刻P 、Q 间(P 、Q 除外)只有一个质点的位移大小等于振幅。

[解析] (1)由题意，t ＝0时的波形如图1(a)所示，t ＝0.6 s 时的波形如图(b)所示：图1若波从P 传向Q ，则t ＝34T ，从而得T ＝0.8 s 。

波传播的周期性和多解问题1．一列简谐横波在x 轴上传播，如图4所示，实线是这列波在t 1＝0.1 s 时刻的波形，虚线是这列波在t 2＝0.2 s 时刻的波形，求：图4(1)如果此波沿x 轴正方向传播，波速的最小值；(2)如果此波沿x 轴负方向传播，波速的可能值．答案 (1)30 m /s (2)v ＝(80k ＋50) m/s(k ＝0,1,2，3…)解析 (1)由波形图知波长λ＝8 m波沿x 轴正方向传播时，传播距离Δx 满足Δx ＝kλ＋38λ(k ＝0,1,2,3…) 由v ＝Δx Δt知，当k ＝0时波速取最小值． 解得最小波速v min ＝30 m/s(2)波沿x 轴负方向传播时，传播距离Δx ＝kλ＋58λ(k ＝0,1,2,3…) 由v ＝Δx Δt得 v ＝(80k ＋50) m/s(k ＝0,1,2,3…)2．如图5所示，图中的实线是一列简谐横波在t ＝0时刻的波形图，虚线对应的是t ＝0.5 s 时的波形图．求：图5(1)如果波沿x 轴负方向传播，且周期T ＞0.5 s ，则波的速度多大？(2)如果波沿x 轴正方向传播，且周期T 满足0.3 s ＜T ＜0.5 s ，则波的速度又是多少？ 答案 (1)0.12 m /s (2)0.84 m/s解析 (1)如果波沿x 轴负方向传播，且周期T ＞0.5 s ，则波向左传播的距离x ＝14λ＝14×24 cm＝6 cm波速v ＝x t ＝0.06 m 0.5 s＝0.12 m/s (2)如果波是沿x 轴正方向传播的，且周期T 满足0.3 s ＜T ＜0.5 s ，则波向右传播了1个波长多，所以波传播的距离为x ＝34λ＋λ＝74×24 cm ＝42 cm 波速v ＝x t ＝0.42 m 0.5 s＝0.84 m/s.。

波的图像与振动图像的综合及波的多解性问题[学习目标] 1.理解波的图像与振动图像的意义及它们之间的关系.2.理解波的多解性，会分析波的综合问题．一、波的图像与振动图像的综合问题(多选)图1甲为一列简谐横波在t＝2 s时的波形图，图乙为这列波上质点P的振动图像，则下列说法正确的是()图1A．该横波向右传播，波速为0.4 m/sB．t＝2 s时，质点Q的振动方向为y轴负方向C．在2～4 s时间内，质点P沿x轴向右平移2.0 mD．在2～4 s时间内，质点Q通过的路程为10 cm答案AD解析由题图乙知，在t＝2 s时，质点P正通过平衡位置向下振动，根据“上下坡法”可知波向右传播，由题图甲可知波长为λ＝1.6 m，由题图乙可知周期T＝4 s，则波速为v＝λT＝1.64m/s＝0.4 m/s，A正确；质点Q与质点P相差半个波长，故振动方向相反，则t＝2 s时，质点Q沿y轴正方向运动，B错误；质点不会随波迁移，只在平衡位置附近振动，C错误；由题图甲可知振幅A＝5 cm，在2～4 s时间内，质点Q通过的路程为s＝2A＝10 cm，D正确．分析波的图像与振动图像的综合问题，主要有以下两个方面：(1)由振动图像确定波的周期(质点振动周期)，由波的图像确定波长，进而计算波速．(2)先在振动图像中确定与波的图像对应时刻质点的振动方向，然后根据波的图像确定波的传播方向．注意：波的图像对应时刻不一定是振动图像中t＝0的时刻．二、Δt 后波形图的画法1．平移法：算出波在Δt 时间内传播的距离Δx ＝v Δt ，把波形沿波的传播方向平移Δx .如果Δx 较大，可化为Δx ＝nλ＋Δx ′，由于波的空间周期性，可以去整留零，只需平移Δx ′即可，平移波形后一定要注意把图像补画完整．2．特殊点法：找出波形图一个波形中相邻的几个特殊点(如波峰、波谷、平衡位置等点)，画出这些特殊点在Δt 时刻的位置，然后用正、余弦曲线连起来画出波形图，如果Δt 较长，可先表示为Δt ＝nT ＋Δt ′.由于时间的周期性，可以去整留零，只需画出特殊点在Δt ′时刻的波形图．特殊点法适用于特殊时间，Δt 或Δt ′必须为14T 的整数倍才好确定特殊点的位置来画波形．特殊点法画波形图较为简单易行．如图2甲为某波在t ＝1.0 s 时的图像，图乙为参与该波动P 质点的振动图像．图2(1)求该波的波速；(2)画出Δt ＝3.5 s 时的波形． 答案 (1)4 m/s (2)见解析图解析 (1)由题图甲得波长λ＝4 m ，由题图乙得周期T ＝1.0 s ，所以波速v ＝λT ＝4 m/s.(2)法一：平移法由题图乙可知1.0 s 时质点P 向y 轴负方向振动，所以题图甲中的波沿x 轴负方向传播，传播距离Δx ＝v Δt ＝4×3.5 m ＝14 m ＝(3＋12)λ，所以只需将波形沿x 轴负方向平移12λ＝2 m 即可，如图(a)所示法二：特殊点法如图(b)所示，在图中取两特殊质点a 、b ，因Δt ＝3.5 s ＝312T ，舍弃3，取T2，找出a 、b 两质点振动T2后的位置a ′、b ′，过a ′、b ′画出正弦曲线即可．三、波的多解问题1．波的传播方向的双向性形成多解凡是没有指明机械波沿哪个方向传播，就要讨论两个方向的可能性． 2．波的时间的周期性形成多解机械波在传播过程中，t 时刻与t ＋nT (n ＝1,2…)时刻的波形完全重合，即同一波形图可能是不同时刻形成的．3．波的空间的周期性形成多解将某一波形沿波的传播方向平移波长的整数倍的距离，平移后的波形与原波形完全重合，这就是波的空间周期性．4．质点在振动中情况不明形成多解在波动问题中，如讲到某质点在某时刻处于最大位移处，就包含有处于正向最大位移处与负向最大位移处两种可能；讲到质点从平衡位置开始振动，就可能是沿y 轴正方向或负方向两个方向振动．一列简谐横波图像如图3所示，t 1时刻的波形如图中实线所示，t 2时刻的波形如图中虚线所示，已知Δt ＝t 2－t 1＝0.5 s ，图3(1)这列波的周期可能是多大？ (2)这列波可能的波速表达式是怎样的？ (3)若波向左传播，且3T <Δt <4T ，波速为多大？ (4)若波速v ＝68 m/s ，则波向哪个方向传播？ 答案 见解析解析 (1)(2)由题图可知波长λ＝8 m ， 当波向右传播时Δt ＝nT 1＋T 14T 1＝24n ＋1s(n ＝0,1,2，…)v 右＝λT 1＝4(4n ＋1) m/s(n ＝0,1,2，…)当波向左传播时Δt ＝nT 2＋34T 2T 2＝24n ＋3s(n ＝0,1,2，…)v 左＝λT 2＝4(4n ＋3) m/s(n ＝0,1,2，…)．(3)若波向左传播，且3T <Δt <4T 则Δt ＝334T ，T ＝215 s ，v 1＝λT＝60 m/s(4)Δt 内波传播的距离为：x ＝v Δt ＝68×0.5 m ＝34 m ＝414λ，故波向右传播．解决波的多解问题的一般思路1．首先考虑传播方向的双向性：如果题目未说明波的传播方向或没有其他条件暗示，应首先按波传播方向的可能性进行讨论．2．对设定的传播方向，首先确定Δt 和T (或确定Δx 和λ)的关系，一般先确定最简单的情况，即一个周期内(或一个波长内)的情况，然后在此基础上加nT (或nλ)．3．应注意题目是否有限制条件，如有的题目限制波的传播方向，或限制时间Δt 大于或小于一个周期等．所以解题时应综合考虑，加强多解意识，认真分析题意．针对训练 (多选)(2019·天津卷)一列简谐横波沿x 轴传播，已知x 轴上x 1＝1 m 和x 2＝7 m 处质点的振动图像分别如图4甲、乙所示，则此列波的传播速率可能是( )图4A ．7 m/sB ．2 m/sC ．1.2 m/sD ．1 m/s 答案 BC解析 由两质点的振动图像可知，t ＝0时刻，x 1＝1 m 处的质点处于平衡位置向下运动，x 2＝7 m 处的质点位于波峰处，该波的周期为T ＝4 s ．若该简谐横波沿x 轴正方向传播，则两质点间的距离为(n ＋14)λ＝6 m(n ＝0、1、2…)，则λ＝244n ＋1 m ，由波速的公式得v ＝λT ＝64n ＋1 m/s(n ＝0、1、2…)，n ＝0时，v ＝6 m/s ；n ＝1时，v ＝1.2 m/s ；n ＝2时，v ＝23 m/s ，C 正确；若该简谐横波沿x 轴负方向传播，则两质点间的距离为(n ＋34)λ＝6 m(n ＝0、1、2…)，则λ＝244n ＋3 m ，由波速的公式得v ＝λT ＝64n ＋3 m/s(n ＝0、1、2…)，n ＝0时，v ＝2 m/s ；n ＝1时，v ＝67 m/s ，B 正确，A 、D 错误．(多选)一列简谐横波沿直线传播，在波的传播方向上有A 、B 两点．在t 时刻A 、B 两点间形成如图5甲所示波形，在(t ＋3 s)时刻A 、B 两点间形成如图乙所示波形，已知A 、B 两点平衡位置间的距离a ＝9 m ，则下列说法中正确的是( )图5A ．若周期为4 s ，波一定向右传播B ．若周期大于4 s ，波可能向右传播C ．若波速为8.5 m/s ，波一定向左传播D ．该波波速可能的最小值为0.5 m/s 答案 ACD解析 若波向右传播，3 s ＝(n ＋34)T 1(n ＝0,1,2，…)，T 1＝124n ＋3 s ≤4 s ，B 错误；若波向左传播，3 s ＝(n ＋14)T 2(n ＝0,1,2，…)，T 2＝124n ＋1 s ．由于n 是整数，当n ＝0，T ＝4 s 时，符合T 1通项，波向右传播，故A 正确；由题图知波长λ＝6 m ，若波速为8.5 m/s ，波在3 s 内传播的距离为x ＝v t ＝8.5×3 m ＝25.5 m ＝414λ，根据波形的平移，波一定向左传播，故C 正确；波在3 s 内传播的最小距离为向左传播1.5 m ，波速可能的最小值为v min ＝1.53m/s ＝0.5 m/s ，故D 正确．1．(波的图像与振动图像的综合应用)(多选)如图6所示，图(a)为一列简谐横波在t ＝0.1 s 时刻的波形图，Q 是平衡位置为x ＝4 m 处的质点，图(b)为质点Q 的振动图像，则下列说法正确的是( )图6A ．该波的周期是0.1 sB ．该波的传播速度为40 m/sC ．该波沿x 轴正方向传播D ．t ＝0.4 s 时，质点P 的速度方向向下 答案 BD解析 由题图(a)得到该波的波长为λ＝8 m ，由题图(b)得到该波的周期为T ＝0.2 s ，所以波速为v ＝λT ＝80.2 m/s ＝40 m/s ，故A 错误，B 正确；t ＝0.1 s 时，Q 点处在平衡位置，且向下振动，根据波形平移法可知该波沿x 轴负方向传播，故C 错误；根据振动规律可知t ＝0.4 s 时，质点P 的速度方向向下，故D 正确．2.(Δt 后波形图的画法)如图7所示为一列沿x 轴负方向传播的简谐横波在某一时刻的图像，请画出再经过14T 后的波的图像．(T 为波源的振动周期)图7答案 见解析图解析 将图像沿x 轴负方向平移14个波长，如图虚线所示．3．(波的多解问题)(多选)(2020·南昌期中)一列简谐横波沿直线由A 向B 传播，A 、B 相距0.45 m ，如图8所示是A 处质点的振动图像．当A 处质点运动到波峰位置时，B 处质点刚好到达平衡位置且向y 轴正方向运动，这列波的波速可能是( )图8A ．4.5 m/sB ．3.0 m/sC ．1.5 m/sD ．0.5 m/s 答案 AD解析 由题图可知周期为0.4 s ．由题可知A 、B 间距和波长的关系为x ＝(n ＋14)λ，再由公式v＝λT 得v ＝ 4.54n ＋1 m/s(n ＝0,1,2，…)，当n ＝0时，v ＝4.5 m/s ，当n ＝1时，v ＝0.9 m/s ，当n ＝2时，v ＝0.5 m/s ，选项A 、D 正确．4.(波的多解问题)(2021·绵阳南山中学高二月考)一列简谐横波沿x 轴正方向传播，t ＝0时刻的波形如图9中实线所示，t ＝0.1 s 时刻的波形如图中虚线所示．波源不在坐标原点O ，P 是传播介质中平衡位置离坐标原点2.5 m 处的一个质点．则以下说法正确的是( )图9A ．质点P 的振幅为0.05 mB ．波的频率可能为0.75 HzC ．波的传播速度可能为50 m/sD ．在t ＝0.1 s 时刻，平衡位置与质点P 平衡位置相距5 m 处的质点一定沿x 轴正方向运动 答案 C解析 质点P 的振幅为0.1 m ，故A 错误；波沿x 轴正方向传播，则Δt ＝nT ＋T4，周期为T＝0.44n ＋1(s)(n ＝0,1,2，…)，f ＝1T ＝4n ＋10.4 (Hz)，所以波的频率可能为2.5 Hz ，12.5 Hz,22.5 Hz ，…，B 错误；波速v ＝λf ＝4×4n ＋10.4 m/s ＝(40n ＋10) m/s ，当n ＝1时，v ＝50 m/s ，C 正确；质点只能在其平衡位置附近振动，不可能沿x 轴正方向运动，故D 错误．。