电场中的电势分布与等势面

静电场与电势分布的电场线和等势面计
$number {01} 汇报人：XX
2024-01-25
算方法研究
目录
• 静电场基本概念与性质 • 电势分布及其表示方法 • 电场线计算方法研究 • 等势面计算方法研究 • 静电场与电势分布关系探讨 • 总结与展望
01
静电场基本概念与性质
静电场定义及特点
01
连续分布的电荷产生的电场可通 过积分计算得到。
点电荷产生的电场强度与距离的 平方成反比，方向沿径向指向点 电荷。
电偶极子产生的电场在远处可近 似为点电荷产生的电场，在近处 则表现为复杂的分布。
静电场中的导体和绝缘体
在静电场中，导体和绝缘体表现出不同的性质
导体内部存在自由电荷，当导体处于静电平衡状态时，其内部电场为零，电荷只分 布在导体表面。
电荷分布
电荷分布的不均匀性会导致电势分布的不均匀，如电 荷密集区域电势较高。
边界条件
不同边界条件下，静电场对电势分布的影响不同，如 接地导体表面电势为零。
不同形状导体周围电势分布特点
点电荷
点电荷周围电势分布呈球形对称，电势与距离 成反比。
线电荷
无限长直线电荷周围电势分布呈圆柱形对称， 电势与距离对数成正比。
据电势的分布情况，选择合适的等势面并进行绘制。
绘制结果
通过计算得到的等势面可以清晰地展示出导体周围的电场分布情况。同时，我们还可以利用这些 等势面来分析导体周围的电场强度和电势梯度等相关物理量。
05
静电场与电势分布关系探讨
静电场对电势分布影响
静电场强度
电场强度越大，电势梯度也越大，导致电势分布不均 匀。
01
在同一等势面上移动电荷时
电场力不做功。

正电荷在电势越高的地方电势能越大，负电荷在电势越高的地方电势能越小。（正电荷的电势能与电势的
关系和物体的重力势能与高度之间的关系相似）。
（3）沿电场线方向电势逐渐降低。
[例题]电子在一条电场线上从a点运动到b点，电势能增加，试判定a、b两点电势高低。
方法一、利用电场线方向来判断
C、沿电场线方向电势逐渐降低；
D、沿电场线方向移动电荷电势能逐渐减小。
（4）关于等势面的说法中正确的是： [ ]
A、电荷在等势面上移动时不受电场力的作用，所以不做功；
B、等势面上各点的场强大小相等；
C、等势面一定跟电场线垂直；
D、两等势面永不相交。
C、电场强度大的地方，其电势也一定较高；
D、沿着电场强度方向，电势逐渐降低。
8、两个带电小球，电量分别为+q和-q，固定在一个长度为L的绝缘杆两端，置于电场强度为E的匀强电场
C、沿电场线方向电势逐渐降低；
D、沿电场线方向移动电荷电势能逐渐减小。
（4）关于等势面的说法中正确的是： [ ]
A、电荷在等势面上移动时不受电场力的作用，所以不做功；
B、等势面上各点的场强大小相等；
C、等势面一定跟电场线垂直；
D、两等势面永不相交。
象。
（3）导体的静电平衡：
① 静电平衡状态：静电感应中，当感应出现的正、负电荷产生的附加场强E'大小等于外场强E0时，合
场强E等于零，导体内部没有电荷定向移动的状态。
② 导体静电平衡的条件：导体内部的合场强处处为零。
③ 导体静电平衡的特点：净电荷只能分布在导体的外表面；电场垂直于导体的外表面；整个导体是一个
参考答案：（1）D ； （2）CD ； （3）D 。

二、等势面
电场中电势相等的点构成的面叫等势面 点电荷形成的电场，等势面是以点电荷为圆心的同心球面
等势面有什么性质？
等势面的几个性质：
（1）在等势面上移动电荷，电场力做功为零； （2）等势面与电场线处处垂直； （3）等势面间的疏密程度表示了场强的大小；等势面的法线表示了 电场的方向， （4）电场线的方向是电势降低的方向。
（5）匀强电场的等势面是一组相互平行的疏密均匀的平面；
3.几种常见电场的等势面分布图谱：
三、尖端放电
1、电荷在表面具有凸出尖端的带电导体上的分布： 电荷有趋尖端性，即尖端电荷密度最大，场强很大
2、尖端放电： 带电较多的导体，尖端部位场强可大到使周围空气发生电离 而引起放电的程度，这就是尖端放电现象。
一、电势
第二节 电势与等势面
1、电势定义：电荷在电场中某点的电势能跟电荷量的比值，
叫做该点的电势 2、电势表达式：
Ep Aq
上式表明：电场中某点电势在数值在等于单位正电荷在该点
具有的电势能
3、电势的单位： 国际单位制 伏特 V
注意： 1、电势是标量
1V = 1J/C
2、电势是从匀强电场中得出的结论，对非匀强电场也适用
3、电势具有相对性,通常选距离电荷无穷远处为零势能位 置，在实际问题中也常选地球（线的方向电势越来越低 （2）由电势和电势能的关系来判断：先由电场力做功 情况判断电势能的变化，再由电势和电势能的关系来 判断电势的升降情况。 （3）根据场源电荷的电场来判断。离场源正电荷越近 的点，电势越高，离场源负电荷越近的点，电势越低。
3、尖端放电现象的应用： 避雷针就是应用尖端放电原理来防止雷击造成危害的。
4、避雷针的防雷击原理：

电势差、电势、电势能、等势面知识归纳一．电势差U AB 的理解电势差： 电荷在电场中两点间移动时，电场力所做的功跟它的电量的比值，叫这两点间的电势差．1．电势差与电场力做功：类比着在重力场中重力做功与高度间的关系，得出电场力做功与电势差的关系． W AB = qU AB 其中U AB =qW AB 是由电场及A 、B 两点位置确定的物理量． 与被移动的电荷无关，与路径无关，与零电势面选择无关．2．公式U AB = qW AB ，标量的正负不表示大小，计算时可以把W AB 和q 都代入正、负号进行计算． 也可以W AB 和q 只代绝对值求出U AB 的绝对值．U AB = -U AB ． 单位伏(V)即1 V= 1 J/C(3)电势差是从能量的角度反映电场性质的物理量．二．电势φ： 电场中某点的电势等于该点与参考点之间的电势差．也等于单位正电荷由该点移到参考点时电场力所做的功．1．电势具有相对性，必须先确定零电势参考点，才能确定电场某点的电势值． 一般取大地或无穷远的电势为零电势U ∞= 0，电势的大小由电场本身和零电势位置决定．2．电势是描述电场能的性质的物理量．3．电势是标量，有“+”、“-”号，正值表示该点的电势高于零，即φA ＞0；负值表示该点的电势小于零，即φA ＜0；电势正负号表示大小比较关系．当规定U ∞= 0时，正电荷形成的电场中各点的电势均为正值．负电荷形成的电场中各点的电势均为负值．4．公式：φA =E A /q ，单位 伏(V) 1 V = 1 J/C5．电势与电势差的关系： U AB ＝φA －φBU AB 为正值时说明φA ＞φB ；U AB 为负值时说明φA ＜φB6．电势和电场线方向的关系：沿着电场线方向电势逐渐降低．7．电势高低变化的判断①根据移动检验电荷做功判断： 移动正电荷电场力做正功(负功)时， 电势降低(升高)； 移动负电荷电场力做正功(负功)时，电势升高(降低)．②根据电场线判断：沿电场线方向电势逐渐降低，逆着电场线方向电势逐渐升高． ③根据场源电荷判断：离场源正电荷越近，电势越高，离场源负电荷越近电势越低．8．电势的叠加：电势是标量，因此点电荷组成电场中某点的电势，等于各个电点荷分别在该点产生的电势的代数和．如等量的异种电荷连线的中垂线上各点的电势为零，等量的同种电荷连线上各点以中点的电势最低，中垂线上各点以连线中点的电势最高，且连线和中垂线上关于该点的对称点等电势．三．电势能E ：电荷在静电场中具有由位置所决定的能．1．电势能是相对的，电势能的值与参考点(零电势能点)的选取有关，电势能零点的选取与电势零点的选取相同． 电势能不能作为描述电场性质的物理量，这是因为电势能的大小、正负都与检验电荷有关．2．电场力做功的四种计算方法①定义式计算法：W AB =Fs AB cos θ= qEd AB 此式仅适用于匀强电场，式中E 为电场强度，s AB 为A 、B 两点的距离，d AB 为沿场强方向的位移．②电势变化计算法：W AB = qU AB = q (φA -φB )③电势能变化计算法：W AB = -Δε=εA -εB④动能变化计算法：W AB = ΔE k =21mv B 2－21mv A 2 (此式只适用于电场力做功情况)，其中② ③ ④式不仅适用于匀强电场，也适用于非匀强电场．3．判断电势能变化(或比较电势能大小)的方法①利用εp = q φp 来判断：电势能的正负号是表示大小的，在应用时要把q 和φp 的正负号代入分析．②利用做功正负来判断：不管是正电荷还是负电荷，电场力对正电荷做正功时该电荷的电势能一定减小，反之该电荷的电势能一定增加． (类似于重力做功与重力势能的变化关系．）③用推论判断：正电荷在电势越高的地方电势能越大，负电荷在电势越低的地方电势能越大． a ．W AB = qU AB = q (φA -φB )普遍适用，利用这个公式时，q 、U 都取绝对值，算出的功也是绝对值，功的正负可以由电荷的正负和移动方向来判断，计算时也可将各量的正负号代入，再根据结果的正负号进行判断．b ．W =Eqd 此式只适用于匀强电场，且d 为起止两点的连线在电场方向的投影．4．电场力做功与电势能的变化的关系：电场力做正功时，电荷的电势能减小；电场力做负功时，电荷的电势能增加． 电场力对电荷所做的功等于电荷电势能的减少量，W AB = E A -E B =ΔεAB5．电势能和电势的关系： εp = q φ (φp =qP ) 正电荷在电势越高的地方电势能越大，负电荷在电势越高的地方电势能越小． (正电荷的电势能和电势的关系与物体的重力势能和高度的关系相同，而负电荷则相反．)四．等势面：电场中电势相等的点集合成的曲面．1．等势面是为了形象地描述电场能的性质(电场中各点的电势分布)引用的假想的图，它不是电场中实际存在的面或线．2．等势面的特点①等势面一定跟电场线垂直．②在同一等势面上移动电荷电场力不做功．③电场线总是从电势高的等势面指向电势低的等势面．④任意两个等势面都不会相交．⑤等差等势面越密的地方电场强度越大．3．几种电场等势面的分布： 匀强电场、点电荷形成的电场、等量异种电荷的电场，等量同种电荷的电场、带电导体周围的电场．。

b
d
0
+
d +
表面上: Ued E dl 0
+ l1 + l2 b+
U U U U a b d e
●整个导体连同表面为一个等势体。
15
e
二、导体上的电荷分布
1.实心导体 电荷只分布在导体表面，导体内部电荷为零。 证明：在导体内作任意高斯面
§17-5
等势面、场强与电势梯度的关系
一、等势面（电势分布的图示法）
●电场中电势相等的点所构成的曲面 1.等势面的规定 ●电场中任意相邻的两等势面之 间的电势差相等。
EE
a
b
c
U U U U U U U const c b a c b b a
U 例：点电荷场 P
1
P 2
E d l E n
5
在直角坐标中:
dU El dl
U Ez z
U Ex x
U Ey y
E dl
U U U ˆ ˆ ˆ E ( i j k ) gradU x y z
电势为标量，易于计算，而由关系
E g r a d UU 可更方便地求得 E 。
U const ,E 0 不是指等势面上
7
三、场强与电势梯度关系的应用 q ，求 E 例1：已知点电荷的电势 U 4 0 r 2 2 2 解： r x y z Y q U 2 2 2 + 4 x y z 0
U q x E x 2 2 2 3 / 2 x 4 ( x y z ) 0 U q y E y 2 2 2 3 / 2 y 4 ( x y z ) 0

电场中的电势分布知识点总结电场是物理学中一个重要的概念，描述了电荷之间相互作用的力场。

在电场中，电势分布是一个关键的概念，它描述了不同位置的电势大小和分布规律。

本文将从以下几个方面总结电场中的电势分布的知识点。

一、电势的定义和计算方法电势是描述电场中位置处势能大小的物理量。

在电势分布的计算中，我们常用到电势差的概念。

电势差表示从一个位置到另一个位置的电势变化量，可以通过电势差公式进行计算。

电势差的单位是伏特(V)。

二、电势分布的规律1. 点电荷电势分布规律在电场中，一个静止的点电荷产生一个以其为中心的球对称电势分布。

电势的大小与距离点电荷的距离成反比，距离越远，电势越小。

2. 均匀带电圆盘电势分布规律在电场中，均匀带电圆盘的电势分布具有轴对称性。

轴线上的位置电势为0，离轴线越远，电势越小。

离开圆盘足够远的点，电势趋近于0。

3. 均匀带电球电势分布规律在电场中，均匀带电球的电势分布具有球对称性。

球心处的电势为常数，离球心越远，电势越小。

球外点的电势与点电荷相同，与均匀带电圆盘相比，球外点电势的分布更加均匀。

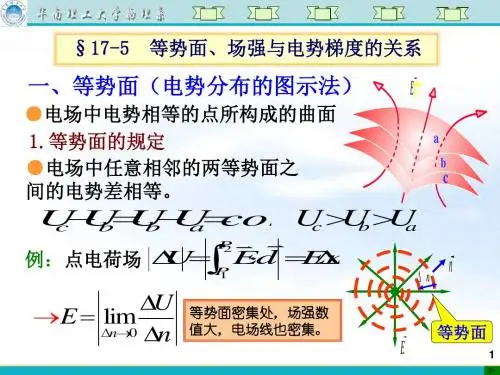
三、等势面的特点等势面是指在电场中，电势相等的点所构成的曲面。

等势面与电场线垂直。

等势面的间距表示电势差的大小，间距越短，电势差越大。

等势面间距均匀表示电势分布均匀，间距不均匀表示电势分布不均匀。

四、静电平衡和电势分布的关系静电平衡的条件是电荷处于电势最小的位置，即力场对电荷所作的虚功为零。

电势分布的不均匀性会导致电荷受到不平衡的力，使系统失去静电平衡。

因此，电势分布的均匀性是维持静电平衡的重要条件。

总结：电势分布是描述电场中电势大小和分布规律的重要概念。

电势的计算可以通过电势差公式进行，不同几何形状的带电物体具有不同的电势分布规律。

等势面与电场线垂直，间距均匀表示电势分布均匀。

电势分布的均匀性是系统保持静电平衡的关键条件。

以上就是对电场中的电势分布知识点的总结。

电势分布的理解和应用对于理解静电场的性质和电势能的转化具有重要意义。

[例1] (2012·泉州高二检测)图
2－2－5中K、L、M为静电场中的3个相 距很近的等势面(K、M之间无电荷)。一 带电粒子射入此静电场中后，沿ab cde
轨迹运动。已知电势φ K＜φ L＜φ M，且 图2－2－5
粒子在ab段做减速运动。下列说法中正确的是( )
A．粒子带负电
B．粒子在bc段做加速运动 C．粒子在a点与e点的速度大小相等 D．粒子从c点到d点的过程中电场力做负功
[思路点拨] 电场线跟等势面垂直，只要画出等势面， 即可画出电场线。匀强电场中的电势分布特点：匀强电场 沿任意方向电势均匀降低。
[解析] 题目中只要寻求电势相等 的点即可确定等势面，因φ B＝6 V， φ C＝－6 V，由匀强电场的特点电势均
匀分布知，在BC连线的中点O处的电势 必为0；同理，在AC线段上找一个电势为0的点，把AC线段 等分成三份，在等分点O′处的电势也必为0。连结OO′即
[答案] C
(1)利用电场线与等势面垂直的特点，可以根据等势 面的形状画出电场线，如果已知等势面电势的高低关系， 可以确定电场线的方向。
(2)带电粒子做曲线运动时，运动轨迹总是弯向粒子 受力的方向，从而可以根据运动轨迹的形状判断粒子受 到的电场力的方向，进而可以得知电场力做功的情况及 粒子的速度、动能和电势能的变化情况。
线，方向从高电势指向低电势，所以斜向左下方，如图所示。
答案：见解析
(2)等势面一定跟电场线垂直，即跟场强的方向垂直。 假如不是这样，场强就有一个沿着等势面的分量，这 样在等势面上移动电荷时电场力就要做功。但这是不可能 的，因为在等势面上各点电势相等，沿着等势面移动电荷 时电场力是不做功的。所以场强一定跟等势面垂直。
(3)沿着电场线方向电势越来越低。可见，电场线 不但跟等势面垂直，而且是由电势较高的等势面指向电 势较低的等势面。

D．若电子由P点运动到Q点，电场力做负功
解 场 ， 平行力q析＜的所0直做电，线的子所，负带以所功负有以相电UMN等荷NP＝，，和U有电MMWQ子P＞分M由N0别＝M，此的向是W点即条电是两M分φP件势怎M条＜别＞说什样等0运，φ明么的势N动而＝了关？线到Wφ系N，PNM点，?有N点电＝与匀φ和场PqM强U点＝P方M点电φNQ，场的，W中过故M等程AP＝势中错q线，误U为电M，P
转解析
方法提炼
1.电势高、低常用的两种判断方法 (1)依据电场线的方向―→沿电场线方向电势逐渐降低。
(2)依据 UAB＝WqAB ―→UAB>0，φA>φB，UAB<0，φA<φB。 2．电势能增、减的判断方法 (1)做功判断法―→电场力做正功，电势能减小；电场力做 负功，电势能增加。 (2)公式法―→由 Ep＝qφ，将 q、φ 的大小、正负号一起代 入公式，若 Ep 的正值越大，电势能越大，若 Ep 为负值，其 绝对值越小，电势能越大。 (3)能量守恒法―→在电场中，若只有电场力做功时，电荷 的动能和电势能相互转化，动能增大，电势能减小，反之， 电势能增大。
这条直线上的两点．一带负电的粒 出现题干所述情况，A错误；
子以速度vA经过A点向B点运动，一 带负电的粒子先向右减速后
段时间后，粒子以速度vB经过B点， 且vB与vA方向相反，不计粒子重力， 下列说法正确的是( )．
向左加速，其受力向左，电
场线注方意向:过向a右、，b两故点A点的的电
势高电于场B线点附的近电的势其，B它正电确；
解析：电场线密集的地
方场强大，ቤተ መጻሕፍቲ ባይዱEc<Eb，选 项A错误；沿电场线方向
电势降低，选项B错误；
从a到b的电场线是曲线，

第2节：电势与等势面一、电势1．等势面(1)定义：电场中电势相等的点构成的面。

(2)特点：由于在等势面上电荷受到的电场力跟等势面垂直，所以电荷在同一个等势面上运动时电场力。

2．几种常见电场的等势面三、尖端放电1．定义带电较多的导体，在部位，场强大到使周围的空气发生而引起的现象。

2．尖端放电的应用和防止(1)应用：避雷针是利用的原理来防止雷击的，它的作用是可以中和云层中的部分电荷，更主要的是把云层中的引入地下。

(2)防止：尖端放电会导致高压设备上的电能的损失，所以高压设备中导体的表面要做得尽可能地。

1．自主思考——判一判(1)沿一条电场线方向上的各点，电势不可能相同。

( )(2)电场中某点的电势与E p成正比，与q成反比。

( )(3)电势与电场强度无任何关系。

( )(4)电荷在等势面上移动时不受电场力作用，所以不做功。

( )(5)等势面上各点电势、场强均相同。

( )(6)电场线与等势面垂直。

( )2．合作探究——议一议(1)在电势越高的地方，某电荷的电势能是否越大？(2)为什么等势面一定跟电场线垂直？(3)尖端放电的原因是什么？避雷针的原理是怎样的？1．电势的特点(1)电势的相对性：电场中某点的电势高低与零电势点的选取有关。

通常选无穷远处或地球表面为零电势点。

(2)电势是标量：电势只有大小没有方向。

在规定了零电势点后，电场中各点的电势可能是正值，也可能是负值。

正值表示该点的电势高于零电势；负值表示该点的电势低于零电势。

显然，电势的正负只表示大小，不表示方向。

(3)电势的固有性：电势是反映电场的能的性质的物理量，由电场本身决定，与该点是否放入电荷及电荷的电性和电荷量均无关，这和许多用比值定义的物理量相同，如电场强度。

2．等势面的特点(1)在等势面内移动电荷，电场力不做功。

(2)在空间中两等势面不相交。

(3)电场线总是和等势面垂直，且从电势较高的等势面指向电势较低的等势面。

(4)在电场线密集的地方，等差等势面密集；在电场线稀疏的地方，等差等势面稀疏。

rdr
10
4.2 从电场强度计算电势
v vv 1）运用高斯定理电场的分布： E = E(r )
2) 通过电场强度的积分计算电势：
V =∫
∞
a
r r E ⋅ dl
11
例7-12 半径为 R 的均匀带电球面，带电量为q，求 空间的电势分布。
dl
r
rP R P ∞
12
(r ≤ R) 0 解： E = q 4πε r 2 (r > R) 0
33
p均匀带电球面内外的场强
E内 = 0 Q E外 = 4πε 0 r 2
p均匀带电球面的电势
Q V内 = 4πε 0 R Q V外 = 4πε 0 r
34
p均匀带电球体内外的场强
Qr E内 = 4πε 0 R 3 Q E外 = 4πε 0 r 2
p均匀带电球体外的电势
Q 3R 2 − r 2 V内 = 8πε 0 R 3 Q V外 = 4πε 0 r
dr r O R x P
E
x
25
σ 2 2 解： V = ( x + R − x) 2ε 0 ∂V σ x (1 − ) E = Ex = − = 2 2 ∂x 2ε 0 x +R
26
两均匀带电同心球面，根据电势分布求电场强度分布
27
1）电场弱的地方电势低；电场强的地方电势高吗？
v 2） V = 0 的地方， E = 0 吗？ v v 3） E 相等的地方，V 一定相等吗？等势面上 E
例7-10 均匀带电圆盘，半径为R ，电荷面密度为σ。 求轴线离圆盘中心O距离为x的P点的电势。
dr r O R x P x
9
解：dV =
dq 4πε 0 x 2 + r 2

电场的电势分布电场是指任何具有电荷的物体或系统周围的空间中存在的力场。

电场的电势分布是指在电场中各个位置的电势大小和分布情况。

本文将介绍电场的电势分布的基本概念、计算方法以及与电势分布相关的应用。

一、电势的概念和计算方法1. 电势的概念电势是指单位正电荷在电场中所具有的电位能，用符号V表示，单位为伏特（V）。

在电势能的定义中，我们通常将无穷远处的电势定义为零点。

电场中任意一点的电势可以通过单位正电荷从无穷远处移到该点所做的功来计算。

2. 电势的计算方法若电场是由静止电荷分布形成的，可以通过电势的叠加原理来计算电场中的电势分布。

对于单个点电荷，在与其距离r处的电势为V的位置，其电势可以由库仑定律计算得到：V = k * Q / r其中，k为静电力常量，Q为电荷量，r为与电荷距离。

对于多个电荷的电场，可以将各个点电荷的电势进行叠加求和。

即：V = ∑(k * Q_i / r_i)其中，Q_i为第i个电荷的电荷量，r_i为与该电荷的距离。

二、电势分布的特点与示意图电势分布受到电荷分布和电场强度的影响。

在电场中，电荷越集中、电场强度越大的地方，电势相对较高。

反之，电荷越分散、电场强度越小的地方，电势相对较低。

通常情况下，电场从正电荷流向负电荷，因此电势的降低方向与电场强度的方向相反。

电势分布可以用等势面表示，即在电场中，每个等势面上的电势数值相同。

示意图如下（图中的曲线即为等势面）：[示意图]三、电势分布的应用1. 电势能和电场力电势能是电势与电荷量的乘积，它表示了单位电荷所具有的电势能量。

当电荷在电势差下移动时，可以通过电势能的变化计算所做的功。

电场力可以通过电势的梯度来求得。

梯度表示了电势的变化率，即单位距离内电势的变化量。

电场力的方向与电势降低的方向相反，大小与电势的梯度成正比。

2. 电势分布在电容器中的应用电势分布在电容器中起着重要作用。

电容器通常由两个带电导体板和介质构成。

在均匀电场中，导体板之间的电势差等于电场强度乘以两板之间的距离。

答案（CD）
抄在练习纸反面
【例题】如图所示，A、B、C、D是匀强电场中
一正方形的四个顶点。已知A、B、C三点的电势
分别为UA=15V，UB=3V，UC=-3V，由此可得：
D点的电势UD=
V.
A

D
【答案】 UD=9V.
B
C
3、等势面较密集的地方，场强较大。 （等势面较稀疏的地方，场强较小。）
4、不同等势面在空间不相交。 （怎样证明？）
五、解题方法指导
---------利用等势面性质解题
例题：下列说法是否正确： A、匀强电场中场强处处相等，所以电
势也处处相等； B、电势降低的方向，就是场强方向； C、场强越大的地方，电场线越密； D、场强越大的地方，等势线越密。
+
4、两平行带电平板的等势面， 是垂直 于电场线的一簇平面。
++++++++++++
三、等势面的性质：
1、沿等势面移动电荷，电场力不做功
证明： W q0 (Ua Ub ) 0
a
b
等势面
注意：但在这个过程中，电场力不一定 不做功。（想一想，为什么？）
2、等势面一定和电场线垂直。且电场线 总是由电势较高的等势面指向电势较低 的等势面。
第七节
一、等势面
1、电场中电势相同的各点构 成的面叫等势面。(等势面上的任 一曲线叫做等势线）
2、电势图示法
规定：画等势面时，相邻两个等势面 的电势差为常数。
二、几种典型电场的等势面
1、点电荷的等势面，是以电荷为
球心的一簇球面。
3、一对等量同号点电荷的等势面，是两

电场与电势电场线与等势面的特性电场与电势——电场线与等势面的特性在电磁学中，电场和电势是两个重要的概念。

了解电场与电势的特性对于理解电磁现象以及应用电场力量进行工程设计和科学研究等都具有重要意义。

本文将详细介绍电场和电势的概念、特性以及电场线和等势面的相关知识。

1. 电场的概念和特性电场是指电荷所产生的一种力场。

当一个电荷存在于空间中时，它会在周围形成一个电场。

任何带电体都会对周围的电荷有一定的作用力，这种作用力就是电场力。

电场力的作用方式遵循库仑定律，即电场力与电荷之间的乘积成正比，与两个电荷之间的距离平方成反比。

在电场中，电场线是一种用于描绘电场的图形工具。

电场线的特性如下：- 电场线的切线方向表示了电场点的场方向。

- 电场线与等势面垂直相交。

- 电场线的密度表示了电场的强度。

密集的电场线表示电场强度大，稀疏的电场线表示电场强度小。

2. 电势的概念和特性电势是指电场对单位正电荷所做的功。

电势是一个标量，用V表示，单位是伏特（V）。

每个点的电势是相对于另一个点而言的。

电势具有以下特性：- 电势在空间中存在势能差，即电势能随着位置的改变而改变。

- 电荷在电势为正的方向移动时，会释放出能量；而在电势为负的方向移动时，会吸收外界的能量。

- 电势差的大小表示了电势能的转化情况。

两点之间的电势差等于单位正电荷从一个点到另一个点的做功。

3. 电场线与等势面的关系电场线和等势面是描述电场和电势分布的两个重要工具。

在电场中，电场线和等势面之间具有以下关系：- 电场线和等势面垂直相交。

这是因为电势是标量，没有方向性，而电场线是矢量，有方向性。

因此，电场线和等势面的切线方向必定垂直。

- 电场线的密度表示电场的强度，而等势面的密度表示电势的大小。

密集的电场线和等势面表示电场强度和电势大，而稀疏的电场线和等势面表示电场强度和电势小。

- 在均匀电场中，电场线平行且等间距，而等势面平行且等势差。

这是因为在均匀电场中，电场和等势面的分布是均匀的，不存在强弱变化。

负电荷在电势低旳地方电势能 大，负电荷在电势高旳地方电势能 小。
8、如图所示，在真空中有两个点电荷，Q1=+2×10-8C，Q2=+4×10-8C，它们相距0.3m，求电场中在Q1 Q2连线上距Q1 0.1m旳A点旳场强。
解:
或方向由电荷1指向电荷2
例1、有一点电荷q=-3×10-6C,从电场中旳A点移到B点过程中，克服电场力做功6×10-4J，从B点移到C点过程中静电力做功9×10-4J。（1）以B点为零势点，电荷在A点时旳电势能是多少？（2）假如以C点为零势点，电荷在A点时旳电势能又是多少？

珠穆朗玛峰海拔8848米
A
B
C
D
0V
1V
2V
3V
电势和高度都具有相对性，与参照点旳选择有关，而高度差与参照点旳选择无关。
E
0V
1V
2V
-1V
一、电势差1、定义：电场中两点间电势旳差值，也叫电压
则有
2、公式
或者表达成
显然
3、单位：在国际单位制中，伏（V ) 1V=1J/C
注意：
1、电场线与等势面到处垂直
2、两个等势面不相交
3、在等势面上移动电荷电场力不做功
几种主要旳结论：
1、沿着电场线旳方向电势逐渐降低 （沿场强方向电势逐渐降低）
2、电场力做旳功总等于电势能旳降低许
在电场中，若把q电荷从A点移到B点
W电＝EPA－EPB＝qψA－qψB＝qVAB
3、电场力做功与详细途径无关，只与起始、终止位置旳电势差有关。
等量同种点电荷电场旳电场线和等势面
匀强电场旳电场线和等势面
带电导体周围电场旳电场线和等势面
在等高面上移动物体重力不做功

静电学中电势分布与电场线的关系在静电学中，电势分布和电场线是描述电场分布的两个重要概念。

电势分布是指在电场中不同位置的电势值的分布情况，而电场线则是通过连接电场中各点的箭头表示电场的方向和强度。

电势分布和电场线之间存在着密切的关系，通过研究它们的关系可以更好地理解电场的特性。

首先，电势分布和电场线的形状是相关的。

在一个均匀的电场中，电势分布是等势面（等电势线）呈平行于电场方向的平面，而电场线则是垂直于等势面的直线。

这是因为在一个均匀电场中，电势值在各个位置上是相等的，所以等势线是平行于电场方向的。

而电场线则是从正电荷指向负电荷的方向，垂直于等势面。

其次，电势分布和电场线的密度也是相关的。

在电势分布比较集中的地方，电场线的密度较大；而在电势分布比较稀疏的地方，电场线的密度较小。

这是因为电势分布的集中程度反映了电场的强度，而电场线的密度反映了电场的强度。

当电势分布比较集中时，电场的强度较大，电场线的密度也较大；当电势分布比较稀疏时，电场的强度较小，电场线的密度也较小。

另外，电势分布和电场线的方向也是相关的。

在一个点电荷周围的电势分布是以点电荷为中心的球对称分布，而电场线则是从正电荷指向负电荷的方向。

这是因为点电荷产生的电场是以点电荷为中心的球对称电场，而电场线则是从正电荷指向负电荷的方向，垂直于等势面。

此外，电势分布和电场线的变化趋势也是相关的。

在两个电荷之间的电势分布是从正电荷指向负电荷的方向逐渐降低的，而电场线则是从正电荷指向负电荷的方向逐渐密集起来。

这是因为两个电荷之间的电势差随着距离的增加而减小，所以电势分布逐渐降低；而电场线的密度则随着电势差的减小而增加。

最后，电势分布和电场线的关系还可以通过数学公式来描述。

根据静电学的基本公式，电场强度的负梯度等于电势的梯度，即E = -∇V。

这个公式表明，电势分布的梯度方向与电场强度的方向相反。

因此，可以通过电势分布的梯度来确定电场线的方向和强度。

综上所述，静电学中电势分布和电场线之间存在着密切的关系。

电场在等位面上的电势分布导言：电势（potential）是描述电场中空间各点电势能的物理量。

电势分布是指空间中各点的电势数值分布情况。

在等位面上，表示电势相等的点构成一条曲线，被称为等位线。

本文将探讨电场在等位面上的电势分布及其特点。

一、电势的定义与计算电势是描述电场的一种性质，指的是单位正电荷在某处所具有的电势能。

电势可以通过以下公式进行计算：\[V=\frac{U}{q}\]其中，V表示电势，U表示电势能，q表示单位正电荷。

在电场中，电势随着距离的变化而改变，从而形成了不同点的电势分布。

二、电场在等位面上的特点1. 等位线的定义等位线是指一组在同一等势位上的点构成的曲线。

等势位是一组电势相等的点所在的平面或曲面，被称为等位面。

电场在等位面上的电势分布是描述电势在等位面上的变化情况。

2. 等位线的性质（1）等位线与电场线垂直相交在电场中，电场线表示电场的方向和强度。

等位线与电场线垂直相交，这是因为等位线所表示的点处具有相同电势，而电场线的方向是电场力的方向，两者之间垂直交叉。

（2）等位线的间距在等势面上，等位线的间距越小，表示电势变化越剧烈；间距越大，表示电势变化越缓慢。

在电势分布中，等位线的间距可以反映电场中电势的变化情况。

（3）等位线的曲率等位线一般具有曲率，曲率的大小反映了电势变化的速率。

曲率大的地方，电势变化剧烈；曲率小的地方，电势变化缓慢。

曲率可以通过等位线的弯曲程度来描述。

三、电势分布的实例以两个平行带电板构成的均匀带电场为例，来探讨电势分布在等位面上的表现。

带电板1带正电荷，带电板2带负电荷，它们之间的距离为d。

在两板中间的某一水平面上，构成了一个等势面。

这个等势面是垂直于带电板的平面，带电板上各点电势相等。

在该等势面上，靠近正带电板的区域电势较大，远离正带电板的区域电势较小。

等位线由电势相等的点构成，可以看做离正带电板越远，等位线密度越小；离正带电板越近，等位线密度越大。

同样，离负带电板越近的地方，等位线密度越大；离负带电板越远的地方，等位线密度越小。

b
q0
E dl
a
q0 (ua ub ) 0
(2) 等势面与电力线互相垂直。
E 等势面
(3) 规定相邻两等势面的电势差相等。
等势面密集——电场较强；
等势面稀疏——电场较弱； (4) 电场强度的方向总是指向电势降低的方向。
第8章 静电场
2
二. 电势与电场强度的微分关系
取两个相邻的等势面，等势面法线方向为 n ，设 n 相同，把点电荷从P移到Q，电场力作功为：
EyBiblioteka u yEzu z
E
(u
i
u
j
u
k)
grad(u)
x y z
某点的电场强度等于该点电势梯度的负值，这 就是电势与电场强度的微分关系。
第8章 静电场
5
思考：以下说法对吗？
E大处
E0处
u高 u0
E小处 E均匀处
u低 u 均匀
注意：
E 的大小，取决于 du 的大小，而不是u的大小
dn
如：均匀带电球面内部空间
§8.6 等势面 电场强度和电势的关系
一、等势面 （描绘电势的空间分布）
1. 等势面——在电场中电势相等的点所连成的曲面。 规定：相邻等势面之间电势差相等。
+
+
（点电荷） （无限大平面）
（电偶极子）
第8章 静电场
1
2. 等势面的性质
(1) 沿等势面移动电荷q0，静电力做功为零。
b
Aab a q0E dl
+ +A
+S +
+ B
-
+
+ +
+