宁夏固原市五原中学补习部2021届高三上学期期中考试数学(文)试题

2021年高三上学期期中统考数学（文）试题含答案本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分. 共 4页.满分150分，考试时间120分钟. 考试结束，将试卷答题卡交上，试题不交回.第Ⅰ卷选择题（共60分）注意事项：1.答卷前，考生务必将自己的姓名、准考证号、座号涂写在答题卡上.2.选择题每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，不能答在试题卷上.3.第Ⅱ卷试题解答要作在答题卡各题规定的矩形区域内，超出该区域的答案无效.一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合要求的.1.若，则＝A. B. C. D.2.已知集合，，则A. B. C. D.3.已知向量, ，如果向量与垂直，则的值为A. B. C. D.4.函数的图像为5.如果若干个函数的图象经过平移后能够重合，则称这些函数为“同簇函数”．给出下列函数：①；②；③；④．其中“同簇函数”的是A.①②B.①④C.②③D.③④6.若数列的前项和，则数列的通项公式A. B. C. D.7.已知命题；命题，则下列命题中为真命题的是A. B. C. D.8.已知，满足约束条件，若的最小值为，则A. B. C. D.9.在中,角的对边分别为,且.则A．B．C．D．10.函数是上的奇函数，,则的解集是A . B. C. D.11.定义在上的偶函数满足且，则的值为A. B. C. D.12.设函数，若实数满足则A． B．C． D．第Ⅱ卷非选择题（共90分）二、填空题：本大题共4小题，每小题4分，共16分．把答案填在答题卡中相应题的横线上．13.已知一元二次不等式的解集为,则的解集为. （）14. ．15.设正数满足, 则当 ______时, 取得最小值.16.在中，，，，则．三、解答题：本大题共6小题，共74分.把解答写在答题卡中.解答应写出文字说明，证明过程或演算步骤.17.(本小题满分12分）已知,.(Ⅰ)若,求的值;(Ⅱ)设,若,求的值.18.(本小题满分12分）已知函数和的图象关于轴对称，且.(Ⅰ)求函数的解析式；(Ⅱ)当时，解不等式.19. (本小题满分12分）设是首项为,公差为的等差数列,是其前项和.(Ⅰ) 若，求数列的通项公式；(Ⅱ) 记,，且成等比数列,证明:().20.(本小题满分12分）如图,游客在景点处下山至处有两条路径.一条是从沿直道步行到,另一条是先从沿索道乘缆车到,然后从沿直道步行到.现有甲、乙两位游客从处下山,甲沿匀速步行,速度为.在甲出发后,乙从乘缆车到,在处停留后,再从匀速步行到.假设缆车匀速直线运动的速度为,索道长为,经测量,,.(Ⅰ) 求山路的长;(Ⅱ) 假设乙先到，为使乙在处等待甲的时间不超过分钟,乙步行的速度应控制在什么范围内?21．（本小题满分12分）新晨投资公司拟投资开发某项新产品，市场评估能获得万元的投资收益.现公司准备制定一个对科研课题组的奖励方案：奖金（单位：万元）随投资收益（单位：万元）的增加而增加，且奖金不低于万元，同时不超过投资收益的.（Ⅰ）设奖励方案的函数模型为，试用数学语言表述公司对奖励方案的函数模型的基本要求.（Ⅱ）下面是公司预设的两个奖励方案的函数模型： C B A①；②试分别分析这两个函数模型是否符合公司要求.22．(本小题满分14分)设函数(Ⅰ)当时，求函数的最大值；(Ⅱ)令（），其图象上存在一点，使此处切线的斜率，求实数的取值范围；(Ⅲ)当，时，方程有唯一实数解，求的值．xx11文倾向数学参考答案及评分标准一、二、13. 14. 15. 16.三、17解: (Ⅰ)∵∴又∵,……3分 ∴ , ………………5分∴.…………………6分(Ⅱ)∵a 2b (2cos 2cos ,2sin 2sin )(2,0)αβαβ+=++= ∴即 …………………8分两边分别平方再相加得: ∴ ∴ ……10分∵且 ∴ …………………12分18.解：(Ⅰ)设函数图象上任意一点，由已知点关于轴对称点一定在函数图象上…………………2分代入，得 …………………4分（Ⅱ）由整理得不等式为等价……………………6分当，不等式为，解为………………7分当，整理为,解为……………………9分当，不等式整理为解为.……………………11分综上所述，当，解集为；当，解集为；当，解集为.…………12分19解(Ⅰ)因为是等差数列，由性质知，…………2分所以是方程的两个实数根，解得，………4分∴或即或.……………6分(Ⅱ)证明:由题意知∴∴ …………7分∵成等比数列，∴ ∴ …………8分∴ ∴ ∵ ∴ ∴…10分∴a n a n n na d n n na S n 222)1(2)1(=-+=-+= ∴左边= 右边=∴左边=右边∴()成立. ……………12分20解: (Ⅰ) ∵,∴∴, …………………2分∴[]6563sin cos cos sin sin sin sin =+=+=+-=C A C A C A C A B ）（）（π …………4分 根据得所以山路的长为米. …………………6分(Ⅱ)由正弦定理得() …………8分甲共用时间：，乙索道所用时间：，设乙的步行速度为 ，由题意得，………10分整理得∴为使乙在处等待甲的时间不超过分钟,乙步行的速度应控制在内. …………………12分21．解：（Ⅰ）由题意知，公司对奖励方案的函数模型的基本要求是：当时，①是增函数；②恒成立；③恒成立………3分（Ⅱ）①对于函数模型：当时，是增函数，则显然恒成立 ……4分而若使函数在上恒成立，整理即恒成立，而，∴不恒成立．故该函数模型不符合公司要求． ……7分②对于函数模型：当时，是增函数，则．∴恒成立． ………8分设，则． 当时，()24lg 12lg 1lg 10555e e e g x x --'=-≤=<，所以在上是减函数， ……10分从而．∴，即，∴恒成立．故该函数模型符合公司要求． ……12分22.解：(Ⅰ)依题意，的定义域为，当时，，……………………2分由 ，得，解得;由 ，得，解得或.，在单调递增，在单调递减；所以的极大值为，此即为最大值……………………4分(Ⅱ)，则有在上有解， ∴≥， ………6分所以 当时，取得最小值……………8分(Ⅲ)因为方程有唯一实数解，所以有唯一实数解，……9分 设，则，，所以由得，由得，所以在上单调递增，在上单调递减， . ……………11分若有唯一实数解，则必有11111()ln 011111m g e m m m m m e-=+=⇒=⇒=+---- 所以当时，方程有唯一实数解. ………14分38104 94D8 铘31576 7B58 筘27026 6992 榒•[22646 5876 塶z25325 62ED 拭27919 6D0F 洏237742 936E 鍮24070 5E06 帆33277 81FD 臽h+。

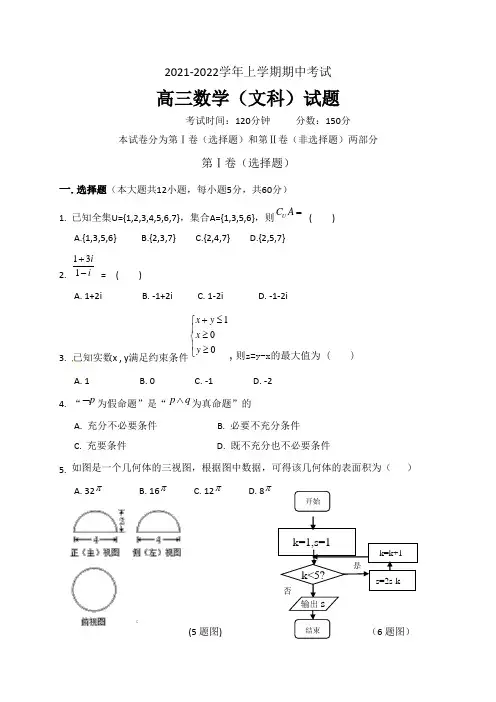
2021-2022学年上学期期中考试高三数学（文科）试题考试时间：120分钟 分数：150分本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分第Ⅰ卷（选择题）一.选择题（本大题共12小题，每小题5分，共60分）1. 已知全集U={1,2,3,4,5,6,7}，集合A={1,3,5,6}，则U C A =( )A.{1,3,5,6}B.{2,3,7}C.{2,4,7}D.{2,5,7}2. 131ii +- = ( )A. 1+2iB. -1+2iC. 1-2iD. -1-2i3. 已知实数x , y 满足约束条件100x y x y +≤⎧⎪≥⎨⎪≥⎩,则z=y-x 的最大值为 ( )A. 1B. 0C. -1D. -2 4. “p ⌝为假命题”是“p q ∧为真命题”的A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件5. 如图是一个几何体的三视图，根据图中数据，可得该几何体的表面积为（ ） A. 32π B. 16π C. 12π D. 8π(5题图) （6题图）是否开始k=1,s=1k<5?输出s结束 k=k+1s=2s-k6. 执行如图所示的程序框图，输出的s 值为 （ ） A. -10 B. -3 C. 4 D. 57. 已知x 与y 之间的几组数据如表：x 0 1 2 3 y267则y 与x 的线性回归方程y b x a ∧∧∧=+必过点 ( )A. (1,2)B. (2,6)C. (315,24) D. (3,7)8. 下列函数中，在定义域内与函数3y x =的单调性与奇偶性都相同的是 （ ）A. sin y x =B. 3y x x =-C. 2x y =D.2lg(1)y x x =++9. 对于使()f x N ≥成立的所有常数N 中，我们把N 的最大值叫作()f x 的下确界．若,a b ∈(0, +∞),且2a b +=，则133a b +的下确界为 （ ） A. 163 B. 83 C. 43 D. 2310.如图所示的数阵中，每行、每列的三个数均成等差数列．如果数阵中111213212223313233a a a a a a aa a ⎛⎫ ⎪ ⎪ ⎪⎝⎭所有数的和等于36，那么22a = （ ）A. 8B. 4C. 2D. 111.三棱锥P-ABC 的侧棱PA 、PB 、PC 两两垂直，侧面面积分别是6，4，3，则三棱锥的体积是 （ ）A. 4B. 6C. 8D.1012.函数()f x 的定义域为R ，f(0)=2,对x R ∀∈，有()()1f x f x '+>，则不等式()1x xe f x e >+ 的解集为 （ ） A. {}|0x x > B. {}|0x x < C. {}|11x x x <->或 D. {}|10x x x <->>或1第Ⅱ卷（非选择题）二．填空题（本大题共4小题，每小题5分，共计20分）13.已知-向量a 与b 的夹角为60°，且a =（-2，-6），10b =，则ab =14.已知数列{}n a 是等比数列，且1344,8a a a ==，则5a 的值为15.抛物线2(0)y ax a =<的焦点坐标为 16.将边长为2的等边∆ABC 沿x 轴正方向滚动，某时刻A 与坐标原点重合（如图），设顶点(,)A x y 的轨迹方程是y=f(x)，关于函数y=f(x)有下列说法：①f(x)的值域为[0，2]； ②f(x)是周期函数且周期为6 ; ③()(4)(2015)f f f π<<;④滚动后，当顶点A 第一次落在x 轴上时，f(x)的图象与x 轴所围成的面积为833π+．其中正确命题的序号为三．解答题(本大题共6道题,共70分,解答应写出文字说明，证明过程或演算步骤) 17.(本小题12分）在∆ABC 中，内角A,B,C 的对边分别为,,a b c .已知3cos 3cos c b C c B =+（I ）求sin sin C A 的值 (II)若1cos ,233B b =-=，求∆ABC 的面积。

宁夏固原市五原中学补习部2021届高三数学上学期期中试题 理（无答案）一、选择题：本题共 12 小题，每小题 5 分，共 60 分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．若集合}{2-==x y y M ，}1{-==x y y P ，那么=P M （ C ）A ．),1(+∞B ．),1[+∞C ．),0(+∞D ．),0[+∞2．设f (x )＝ln x ＋x －2，则函数f (x )的零点所在的区间为( B ) A ．(0，1) B ．(1，2) C ．(2，3) D ．(3，4) 3．将函数sin()3y x π=-的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变）， 再将所得的图象向左平移3π个单位，得到的图象对应的解析式是（ C ） A ．1sin 2y x = B ．1sin()22y x π=-C.1sin()26y x π=-D.sin(2)6y x π=-4．若x ＝－2是函数f (x )＝(x 2＋ax －1)·e x －1的极值点，则f (x )的极小值为( A ) A.－1B.－2e －3C.5e －3D.15．高为H ，满缸水量为V 的鱼缸的轴截面如图所示，其底部破了一个小洞，满缸水从洞中流出，若鱼缸水深为h 时水的体积为v ，则函数v ＝f (h )的大致图象是( B )6．若a >b ，则( D ) A.ln(a －b )>0 B.3a <3bC. |a |>|bD.|a 3－b 3>07．设3.0log 2.0=a ，3.0log 2=b 则( B )A ．0<<+ab b aB ．0<+<b a abC ．ab b a <<+0D ．b a ab +<<08．已知定义在R 上的奇函数()f x 满足：当0x ≥时，()1e exx f x =-.若不等式()()242f t f m mt->+对任意实数t 恒成立，则实数m 的取值范围是 ( A ) A.(),2-∞- B ．()2,0- C ．()(),02,-∞+∞ D ．()(),22,-∞-+∞9．已知函数f (x )＝|2x－1|，a <b <c 且f (a )>f (c )>f (b )，则下列结论中，一定成立的是( D ) A.a <0，b <0，c <0 B.a <0，b ≥0，c >0 C.2－a<2cD.2a ＋2c<210．若函数)12()2()(2+++-=m mx x m x f 的两个零点分别在区间(-1，0)和区间(1，2)内，则m 的取值范围是( C ) A ．(21-，41) B ．(41-，21) C ．(41，21) D ．⎥⎦⎤⎢⎣⎡2141， 11．函数f (x )＝sin xln （x ＋2）的图象可能是( A )12.已知函数y ＝f(x)在R 上可导且f(0)＝2，其导函数f'(x)满足()()2f x f x x '-->0，对于函数g(x)＝()x f x e，下列结论错误．．的是( D ) A.函数g(x)在(2，＋∞)上为单调递增函数 B.x ＝2是函数g(x)的极小值点 C.函数g(x)至多有两个零点 D.x ≤0时，不等式f(x)≤2e x 恒成立 二、填空题（本大题共4小题，每题5分，共20分.）13．已知2'()2(2)f x x xf =+，则曲线()y f x =在点(1,(1))f 处的切线方程为 . 610x y ++= 14.设f (x )＝⎩⎪⎨⎪⎧x 2，x ∈[0，1]，1x ，x ∈（1，e](e 为自然对数的底数)，则⎰=e dx x f 0)(____34____15.奇函数()f x 满足()()11f x f x +=-，当01x <≤时，()()2log 4f x x a =+，若1522f ⎛⎫=-⎪⎝⎭，则()a f a +=_____2______.16.定义：如果函数)(x f y =在定义域内给定区间b][，a 上存在)(00b x a x <<，满足ab a f b f x f --=)()()(0，则称函数)(x f y =是b][，a 上的“平均值函数”，0x 是它的一个均值点。

2021年高三上学期中段考试数学（文）试题 含答案选择题：本大题共10小题，每小题5分，满分50分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．的值为 ( ) A ．B ．C ．D ．2．设全集(){}{},30,1,U R A x x x B x x ==+<=<-集合集合则右图中阴影部分表示的集合为 （ ） A. B. C. D.3. 条件P ：x <-1，条件Q ：x <-2，则P 是Q 的 （ ）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件4.．在复平面内为坐标原点, 复数与分别对应向量和,则=（ ） A. B. C. D.5. 函数的定义域是 （ ） A ．（，） B ．(，） C ．(，1） D ．(，）6.. 已知函数，且，则的值是（ ） A. B. C. D.7.奇函数满足，且当时，，则的值为（ ）A. 8B.C.D.8．当时，下列大小关系正确的是( )A. B. D. D.9．客车从甲地以60km/h的速度匀速行驶1小时到达乙地，在乙地停留了半小时，然后以80km/h的速度匀速行驶1小时到达丙地．下列描述客车从甲地出发，经过乙地，最后到达丙地所经过的路程与时间之间关系的图象中，正确的是（）10．观察下列事实|x|+|y|=1的不同整数解（x,y）的个数为4 ， |x|+|y|=2的不同整数解（x,y）的个数为8， |x|+|y|=3的不同整数解（x,y）的个数为12 ….则|x|+|y|=20的不同整数解（x，y）的个数为（）A.76B.80C.86D.92二、填空题：本大题共4小题，考生作答4小题，每小题5分，满分20分．11．已知△ABC中，角A、B、C的对边分别为、、c且，，，则 .12．执行如右图所示的程序框图，若输入的值为6，则输出的值为13．已知满足约束条件，则的最大值是14.已知是内任意一点，连结，，并延长交对边于，，，则，这是平面几何中的一个命题，运用类比猜想，对于空间四面体中,若四面体内任意点存在什么类似的命题三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．15．（本小题满分12分）已知向量，（1）求向量与向量的夹角；（2）若向量满足：①；②，求向量.16．（本题满分13分）已知：函数，为实常数．(1) 求的最小正周期；(2)在上最大值为3，求的值.17．（本小题满分13分）如图6，某测量人员，为了测量西江北岸不能到达的两点A，B之间的距离，她在西江南岸找到一个点C，从C点可以观察到点A，B；找到一个点D，从D点可以观察到点A，C；找到一个点E，从E点可以观察到点B，C；并测量得到数据：，，，，，DC=CE=1（百米）. （1）求 CDE的面积；（2）求A，B之间的距离.18.（本小题满分14分）已知函数，曲线在点处的切线为:，且时,有极值.（1）求的值；（2）求函数在区间上的最大值和最小值.19.（本小题满分14分）（1）已知是公差为的等差数列，是与的等比中项，求该数列前10项和；（2）若数列满足，，试求的值.20．（本小题满分14分）已知是实数，函数，如果函数在区间上有零点，求的取值范围．五校联考xx学年高三第一学期期中考试文科数学试题答题卡一、选择题（每题5分,共40分）二．填空题（每题5分，共30分）11._____________________ 12.____________________ 13._____________________ 14.____________________三．解答题（共80分）15.解：(1)(2)(2)17.解：(1) (2)(2)19.解：（1）（2）（2）一．选择题（每题5分,共50分）三．解答题（共80分）16.解： .............2分.............4分.............6分（2）由（1）得且由可得 .............8分.............10分则 .............11分.............13分18.解：切线的斜率，，将代入切线方程可得切点坐标，根据题意可联立得方程解得（2）由（1）可得，令，得或.极值点不属于区间,舍去.分别将代入函数得.19.解:(1)设数列的首项为,公差为,则.根据题意,可知道,即(解得(2)解法一:由,经化简可得...........2分...........4分...........6分...........7分...........8分...........9分...........10分...........11分...........12分...........13分...........14分...........1分...........3分...........4分...........6分...........7分...........9分数列是首项为,公差为的等差数列..解法二:分别把代入可得:,,,,, 因此,猜想. . 20解: 若 ， ，显然在上没有零点， 所以 ...2分令 得当 时， 恰有一个零点在上； ...5分当 即 时， 也恰有一个零点在上；...8分当 在上有两个零点时， 则()()208244011121010a a a a f f >⎧⎪∆=++>⎪⎪-<-<⎨⎪≥⎪⎪-≥⎩ 或()()208244011121010a a a a f f <⎧⎪∆=++>⎪⎪-<-<⎨⎪≤⎪⎪-≤⎩ ..12分解得或 ..13分因此的取值范围是 或 ； ..14分...........10分 ...........13分 ...........14分 ...........10分 ...........13分 ...........14分_; 20779 512B 儫31773 7C1D 簝 38555 969B 際39894 9BD6 鯖b F"236684 8F4C 轌o。

宁夏2021年高三上学期数学期中考试试卷（II）卷姓名:________ 班级:________ 成绩:________一、填空题 (共14题；共14分)1. （1分）(2017·江苏模拟) 已知集合U={1，2，3，4，5，6，7}，M={x|x2﹣6x+5≤0，x∈Z}，则∁UM=________．2. （1分） (2017高二上·泰州开学考) 函数的定义域为________．3. （1分） (2020高一下·金华期末) 若是角终边上一点，则 ________；________.4. （1分） (2020高一下·吉林月考) 对于，有如下命题：①若，则为等腰三角形；② ，则为直角三角形；③若，则为钝角三角形，其中正确命题的序号是________.5. （1分）已知=（a，﹣2），=（1，2﹣a），且∥，则a=________6. （1分）已知等差数列{an}的前n项和为Sn ，若S12=21，则a2+a5+a8+a11________7. （1分）(2017·四川模拟) 在平面直角坐标系xOy中，已知P是函数f（x）=ex（x＞0）的图象上的动点，该图象在点P处的切线l交y轴于点M，过点P作l的垂线交y轴于点N，设线段MN的中点的纵坐标为t，则t的最大值是________．8. （1分） (2016高三上·新疆期中) “直线ax+2y+1=0和直线3x+（a﹣1）y+1=0平行”的充要条件是“a=________”．9. （1分） (2017高一下·乾安期末) 已知向量，，且，则m=________．10. （1分）(2020·泰州模拟) 若函数只有一个零点，则实数a的取值范围为________.11. （1分） (2015高三上·巴彦期中) 已知△AB C的三边长AC=3，BC=4，AB=5，P为AB边上任意一点，则的最大值为________12. （1分） (2018高二下·雅安期中) 某产品的销售收入（万元）是产量x（千台）的函数，生产成本（万元）是产量x（千台）的函数，已知，为使利润最大，应生产________（千台）．13. （1分）已知数列{an}满足a1=1，an+1•an=2n（n∈N*），则S2012=________14. （1分） (2020高二上·东莞开学考) 已知在中，，，，，，则的值为________.二、解答题 (共6题；共13分)15. （2分）设函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，﹣＜φ＜，x∈R）的部分图象如图所示．（1）求函数y=f（x）的解析式；（2）当x∈[﹣，]时，求f（x）的取值范围．16. （2分） (2018高一上·牡丹江期中) 已知命题p：，命题q:|2a-1|<3．（1）若命题p是真命题，求实数a的取值范围；（2）若p∨q是真命题，p∧q是假命题，求实数a的取值范围。

宁夏2021版高三上学期期中数学试卷（文科）（I）卷姓名:________ 班级:________ 成绩:________一、选择题 (共8题；共16分)1. （2分） (2017高二下·景德镇期末) 已知集合A={x|y=ln（x﹣1）}，B={x|﹣1＜x＜2}，则（∁RA）∩B=（）A . （﹣1，1）B . （﹣1，2）C . （﹣1，1]D . （1，2）2. （2分） (2019高一上·湖北月考) 下列四个函数中，在上为增函数的是（）A .B .C .D .3. （2分） (2020高二上·湛江期末) 已知命题，，则是（）．A . ，B . ，C . ，D . ，4. （2分） (2017高二下·正定期末) 已知是等比数列，，，则公比等于（）A .B .C .D .5. （2分） (2016高一下·武城期中) 已知θ是第三象限角，且sin4θ+cos4θ= ，那么sin2θ等于（）A .B . -C .D . -6. （2分） (2016高三上·洛宁期中) m，n是两条不同的直线，α，β是两个不同的平面，下列命题是真命题的是（）A . 若m∥α，m∥β，则α∥βB . 若m∥α，α∥β，则m∥βC . 若m⊂α，m⊥β，则α⊥βD . 若m⊂α，α⊥β，则m⊥β7. （2分） (2016高二上·大庆期中) 设双曲线的离心率e=2，右焦点为F（c，0），方程ax2+bx﹣c=0的两个实根分别为x1和x2 ，则点P（x1 ， x2）满足（）A . 必在圆x2+y2=2内B . 必在圆x2+y2=2外C . 必在圆x2+y2=2上D . 以上三种情形都有可能8. （2分） (2019高一上·株洲月考) 已知在长方体中，底面是边长为2的正方形，高为4，则点到截面的距离是（）A .B .C .D .二、填空题 (共7题；共7分)9. （1分） (2016高一上·鼓楼期中) 计算27 的结果是________．10. （1分） (2017高二下·红桥期末) 如果函数f（x）=sin（）（ω＞0）的最小正周期为，则ω的值为________．11. （1分）已知某个几何体的三视图如图所示，根据图中标出的尺寸，可得这个几何体的表面积是________12. （1分） (2018高二上·南京月考) 已知焦点在轴上的椭圆的离心率为，且它的长轴长等于圆的半径，则椭圆的标准方程是________.13. （1分） (2019高二下·哈尔滨期末) 给出下列4个命题：①若函数在上有零点，则一定有；②函数既不是奇函数又不是偶函数；③若函数的值域为，则实数的取值范围是；④若函数满足条件，则的最小值为 .其中正确命题的序号是：________.（写出所有正确命题的序号）14. （1分） (2016高二下·新疆期中) 函数y=loga（x+3）﹣1（a＞0，a≠1）的图象恒过定点A，若点A在直线mx+ny+1=0上，其中mn＞0，则 + 的最小值为________．15. （1分） (2016高一下·漳州期末) 已知Sn是等差数列{an}的前n项和，公差为d，且S2015＞S2016＞S2014 ，下列五个命题：①d＞0；②S4029＞0；③S4030＜0；④数列{Sn}中的最大项为S2015；⑤|a2015|＞|a2016|．其中正确结论的序号是________．（写出所有正结论的序号）三、解答题 (共5题；共40分)16. （5分）已知||=4，||=3，，的夹角θ为60°，求：（1）（+2）•（2﹣）的值；（2）|2﹣|的值．17. （5分） (2019高一下·宁波期中) 已知等差数列的公差，前项和 .（I）求的首项；（II）求数列的前项和 .18. （15分） (2020高一下·宝坻月考) 如图所示，已知平面，M，N分别是，的中点， .（1）求证：平面；（2）求证：平面平面；（3）若，，求直线与平面所成的角.19. （10分） (2019高二上·荔湾期末) 已知抛物线经过点．（1）求的标准方程和焦点坐标；（2）斜率为的直线经过抛物线的焦点，且与抛物线相交于，两点，求线段的长．20. （5分）如图，已知点A（11，0），函数y=的图象上的动点P在x轴上的射影为H，且点H在点A 的左侧，设|PH|=t，△APH的面积为f（t）（1）求函数f（t）的解析式及t的取值范围．（2）若a∈（0，2），求函数f（t）在（0，a]上的最大值．参考答案一、选择题 (共8题；共16分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、二、填空题 (共7题；共7分)9-1、10-1、11-1、12-1、13-1、14-1、15-1、三、解答题 (共5题；共40分) 16-1、17-1、18-1、18-2、18-3、19-1、19-2、20-1、。

宁夏 2021 版高三上学期期中数学试卷（I）卷姓名:________班级:________成绩:________一、 填空题 (共 14 题；共 18 分)1. （1 分） (2019 高一上·上海月考) 满足的集合 M 的个数是________个.2. （1 分） (2016 高二上·上海期中) 已知 x∈R，命题“若 2＜x＜5，则 x2﹣7x+10＜0”的否命题是________．3. （2 分） 设 α 是第二象限角，P（x，4）为其终边上一点，且 cosα= ， 则 x=________ ，tanα=________4. （1 分） (2019 高三上·海淀月考) 已知函数数在 ________处取得极值.的导函数有且仅有两个零点,其图像如图所示,则函5. （1 分） (2016 高一上·南城期中) 用二分法求方程 x3+4=6x2 的一个近似解时，已经将一根锁定在区间（0， 1）内，则下一步可断定该根所在的区间为________．6. （1 分） 若函数 f（x）= 7. （1 分） 对于函数， g（x）=f（x）+ax，x∈[﹣2，2]为偶函数，则实数 a=________ 的图象：①关于直线对称；②关于点对称；③可看作是把 y=sin2x 的图象向左平移 个单位而得到；④可看作是把的图象上所有点的纵坐标不变，横坐标缩短到原来的 倍而得到．以上叙述正确的序号是________第 1 页 共 14 页8. （2 分） (2019 高一下·宁波期末) ，则 B=________，中，角的对边分别为的面积 S=________.，已知9. （1 分） (2019 高二下·上海期末) 已知平行六面体，，则 的长为________中，，，，10. （1 分） (2019 高三上·浙江月考) 已知非零向量，满足，，，则对任意实数 ，的最小值为________．11. （1 分） (2016 高二上·长春期中) 函数 f（x）=﹣ x3+x2+4x+5 的极大值为________．12. （1 分） (2016 高一下·成都期中) 已知数列 1，a1 ， a2 ， 9 是等差数列，数列 1，b1 ， b2 ， b3 ，9 是等比数列，则的值为________．13. （2 分） (2019·浙江模拟) 设数列{an}的前 n 项和为 Sn ． 若 S2＝6，an+1＝3Sn+2，n∈N* ， 则 a2＝ ________，S5＝________．14. （2 分） (2017·诸暨模拟) 已知函数 f（x）=x3﹣3x，函数 f（x）的图象在 x=0 处的切线方程是________； 函数 f（x）在区间[0，2]内的值域是________．二、 解答题 (共 6 题；共 50 分)15. （5 分） (2018 高一下·伊通期末) 在平面直角坐标系中，已知向量，，.(Ⅰ)若，求的值；(Ⅱ)若的夹角为 ，求 的值.16. （10 分） (2019 高二上·大庆月考) 已知 ：实数 满足数 满足．（1） 若，且 ， 均正确，求实数 的取值范围；（2） 若是的充分不必要条件，求实数 的取值范围．第 2 页 共 14 页，其中； ：实17. （10 分） (2019 高一下·益阳月考) 已知函数．（1） 求函数的单调增区间；（2） 若锐角的三个角满足，求的取值范围．18. （10 分） (2019 高三上·常州月考) 如图是一个半径为 2 千米，圆心角为 的扇形游览区的平面示意图 是半径 上一点， 是圆弧 上一点，且.现在线段 ，线段 及圆弧 三段所示位置设立广告位，经测算广告位出租收入是：线段处每千米为 元，线段及圆弧处每千米均为 元．设弧度，广告位出租的总收入为 元．（1） 求 关于 的函数解析式，并指出该函数的定义域； （2） 试问： 为何值时，广告位出租的总收入最大？并求出其最大值． 19. （5 分） 已知函数 f（x）=（x2+ax+a）ex（a≤2，x∈R） （1）若 a=1，求 y=f（x）在点（0，f（0））处的切线方程； （2）是否存在实数 a，使得 f（x）的极大值为 3，若存在，求出 a 的值；若不存在，说明理由． 20. （10 分） (2017 高三下·赣州期中) 等差数列{an}的前 n 项和为 Sn ， 已知 a2=7，a3 为整数，且 Sn 的 最大值为 S5 ． （1） 求{an}的通项公式； （2） 设 bn= ，求数列{bn}的前 n 项和 Tn ．第 3 页 共 14 页一、 填空题 (共 14 题；共 18 分)答案：1-1、 考点：参考答案解析： 答案：2-1、 考点：解析：答案：3-1、 考点：第 4 页 共 14 页解析： 答案：4-1、 考点： 解析：答案：5-1、 考点：解析： 答案：6-1、 考点：第 5 页 共 14 页解析： 答案：7-1、 考点： 解析：答案：8-1、 考点：第 6 页 共 14 页解析： 答案：9-1、 考点：解析： 答案：10-1、 考点：第 7 页 共 14 页解析： 答案：11-1、 考点：解析：第 8 页 共 14 页答案：12-1、 考点：解析： 答案：13-1、 考点：解析：答案：14-1、 考点： 解析：第 9 页 共 14 页二、 解答题 (共 6 题；共 50 分)答案：15-1、 考点： 解析：第 10 页 共 14 页答案：16-1、答案：16-2、考点：解析：答案：17-1、答案：17-2、考点：解析：答案：18-1、答案：18-2、考点：解析：答案：19-1、考点：解析：答案：20-1、答案：20-2、考点：解析：。

宁夏固原市五原中学2021届高三中期考试试题数学(理)试题一､选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 若集合{}2M yy x -==∣，{P yy ==∣，那么M P ⋂=（ ）A. (1,)+∞B. [1,)+∞C. (0,)+∞D. [0,)+∞【答案】C 【解析】 【分析】计算集合M 和P ，再计算交集得到答案.【详解】{}210M y y y y x ⎧⎫===>⎨⎬⎩⎭，{{}0P yy y y ===≥∣，故(0,)M P =+∞.故选：C.2. 设()ln 2f x x x =+-，则函数()f x 的零点所在的区间为（ ） A. (0,1) B. (1,2)C. (2,3)D. (3,4)【答案】B 【解析】 【分析】根据()f x 的单调性，结合零点存在性定理，即可得出结论. 【详解】()ln 2f x x x =+-在(0,)+∞单调递增， 且(1)10,(2)ln20f f =-<=>， 根据零点存在性定理，得()f x 存在唯一的零点在区间(1,2)上. 故选：B【点睛】本题考查判断函数零点所在区间，结合零点存在性定理的应用，属于基础题.3. 将函数sin 3y x π⎛⎫=- ⎪⎝⎭的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再将所得的图象向左平移3π个单位，得到的图象对应的解析式是（ ） A. 1sin2y x = B. 1sin 22y x π⎛⎫=-⎪⎝⎭C. 1sin 26y x π⎛⎫=- ⎪⎝⎭D. sin 26y x π⎛⎫=-⎪⎝⎭【答案】C 【解析】【详解】将函数y=sin(x －3π)的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变）得到y=sin(12x －3π)，再向左平移3π个单位得到的解析式为y=sin(12（x+3π）－3π)= y=sin(12x－6π)，故选C 4. 若2x =-是函数21()(1)x f x x ax e -=+-的极值点，则()f x 的极小值为（ ）． A. 1- B. 32e -- C. 35e - D. 1【答案】A 【解析】由题可得()()()()121212121x x x f x x a ex ax e x a x a e ---⎡⎤=+++-=+++-⎣⎦'， 因为()20f '-=，所以1a =-，()()211x f x x x e-=--，故()()212x f x x x e--'=+，令()0f x '>，解得2x <-或1x >，所以()f x 在()(),2,1,-∞-+∞上单调递增，在()2,1-上单调递减， 所以()f x 的极小值为()()1111111f e-=--=-，故选A ．【名师点睛】（1）可导函数y ＝f (x )在点x 0处取得极值的充要条件是f ′(x 0)＝0，且在x 0左侧与右侧f ′(x )的符号不同；（2）若f (x )在(a ，b )内有极值，那么f (x )在(a ，b )内绝不是单调函数，即在某区间上单调增或减的函数没有极值．5. 高为H 、满缸水量为V 的鱼缸的轴截面如图所示，现底部有一个小洞，满缸水从洞中流出，若鱼缸水深为h 时水的体积为v ，则函数()v f h =的大致图像是（ ）A. B.C. D.【答案】B 【解析】 【分析】由函数的自变量为水深h ，函数值为鱼缸中水的体积，得到函数图像过原点，再根据鱼缸的形状，得到随着水深的增加，体积的变化速度是先慢后快再慢的，即可求解.【详解】根据题意知，函数的自变量为水深h ，函数值为鱼缸中水的体积，所以当0h =时，体积0v =，所以函数图像过原点，故排除A 、C ；再根据鱼缸的形状，下边较细，中间较粗，上边较细，所以随着水深的增加，体积的变化速度是先慢后快再慢的，故选B.【点睛】本题主要考查了函数的使用应用问题，其中解答中根据水缸的形状，得到函数的性质是解答的关键，着重考查了分析问题和解答问题的能力，属于基础题. 6. 若a b >，则（ ） A. n 0()l a b ->B. ||||a b >C. 33a b <D.330a b ->【答案】D 【解析】 【分析】根据题目条件，针对各选项分别进行讨论,从而求出答案.【详解】A. 因为a b >，所以0a b ->，当01a b <-<时，ln()0-<a b ，故A 错误； B 若12a b =>=-，所以||||a b <，故B 错误； C. 因为a b >，所以33a b >，故C 错误；D. 因为a b >，所以33a b ≠，所以330a b ->，故D 正确. 故选：D.【点睛】本题主要考查不等式的性质，根据题目条件化简得出结论，当然也可以使用特殊值的方法，本题属于常考题.7. 设0.2log 0.3a =，2log 0.3b =，则 A. 0a b ab +<< B. 0ab a b <+< C. 0a b ab +<< D. 0ab a b <<+【答案】B 【解析】【详解】分析：求出0.2211log0.3,0.3log a b ==，得到11a b+的范围，进而可得结果． 详解：.0.30.3log0.2,2a b log ==0.2211log0.3,0.3log a b ∴== 0.3110.4log a b ∴+= 1101a b ∴<+<,即01a b ab+<<又a 0,b 0><ab 0∴<即ab a b 0<+<故选B.点睛：本题主要考查对数的运算和不等式，属于中档题．8. 已知定义在R 上的奇函数()f x 满足：当0x ≥时，()1e e xxf x =-.若不等式()()242f t f m mt ->+对任意实数t 恒成立，则实数m 的取值范围是( )A. (,-∞B. ()C. ()(),02,-∞+∞D. ((),2,-∞+∞【答案】A 【解析】 【分析】由()f x 是R 上的奇函数，并结合当0x ≥时，()1e exx f x =-，可得()f x 的解析式，进而判断其单调性，可将不等式转化为2420mt t m ++<对任意t ∈R 恒成立，进而可求得实数m 的取值范围.【详解】由题意知，0x <时，0x ->，则()1e e xxf x ---=-， 因为()f x 是R 上的奇函数，所以()()11e e e e xxxx f x f x --⎛⎫=--=--=- ⎪⎝⎭，所以当x ∈R 时，()1e e xxf x =-. 因为函数1xy e =为R 上的减函数，所以1e x y =-为R 上的增函数，故()1e e xx f x =-为R 上的增函数，由()()242f t f m mt->+，可得242t m mt ->+，即2420mt t m ++<对任意t ∈R 恒成立，当0m =时，不等式可化为40t <，显然不符合题意， 所以0m ≠，可得21680m m <⎧⎨∆=-<⎩，解得m <故选：A.【点睛】本题考查奇函数的性质，考查函数单调性的应用，考查不等式恒成立问题，考查学生的计算能力与推理能力，属于中档题.9. 已知函数()|21|,x f x a b c =-<<且()()()f a f c f b >>，则下列结论中，一定成立的是（ ）A. 0,0,0a b c <<<B. 0,0,0a b c <≥>C. 22a c -<D. 222a c +<【答案】D【解析】 【分析】根据题意可画出函数图像，由图像可知要使得a b c <<，且()()()f a f c f b >>，则有()|21|12a a f a =-=-，()|21|21c c f c =-=-，由()()f a f c >，从而得到答案.【详解】作出函数()|21|xf x =-的图象，如图，a b c <<且()()()f a f c f b >>，结合图象知，0()1,0,0f a a c <<<>， 021a ∴<<()|21|12a a f a ∴=-=-()1,01f c c ∴<∴<<022,()|21|21c c c f c ∴<<∴=-=-，又()()f a f c >1221a c ∴->-，222a c ∴+<，故选：D .【点睛】本题考查指数型函数的单调性；函数图像的应用.10. 若函数2()(2)(21)f x m x mx m =-+++的两个零点分别在区间()1,0-和区间()1,2内，则m 的取值范围是（ ） A. 11,24⎛⎫-⎪⎝⎭ B. 11,42⎛⎫-⎪⎝⎭ C. 11,42⎛⎫⎪⎝⎭D. 11,42⎡⎤⎢⎥⎣⎦【答案】C 【解析】 【分析】利用零点存在定理进行列不等式方程组，进而求解即可【详解】函数2()(2)(21)f x m x mx m =-+++的两个零点，根据题意有，(1)(0)0(1)(2)0f f f f -⋅<⎧⎨⋅<⎩，解得1142m << 故选：C 11. 函数()()sin ln 2xf x x =+的部分图象可能是（ ）A. B.C. D.【答案】A 【解析】 【分析】考查函数()y f x =的定义域、在()1,0-上的函数值符号，可得出正确选项.【详解】对于函数()y f x =，2021x x +>⎧⎨+≠⎩，解得2x >-且1x ≠-，该函数的定义域为()()2,11,---+∞，排除B 、D 选项.当10x -<<时，sin 0x <，122x <+<，则()ln 20x +>，此时，()()sin 0ln 2xf x x =<+，故选A.【点睛】本题考查函数图象的识别，一般从函数的定义域、奇偶性、单调性、零点、函数值符号进行判断，考查分析问题和解决问题的能力，属于中等题.12. 已知函数()y f x =在R 上可导且()02f =，其导函数()f x '满足()()02f x f x x '>--，对于函数()()xf xg x e =，下列结论错误．．的是（ ）. A. 函数()g x 在()2,+∞上为单调递增函数 B. 2x =是函数()g x 的极小值点 C. 0x ≤时，不等式()2xf x e ≤恒成立D. 函数()g x 至多有两个零点【答案】C 【解析】 【分析】由()()02f x f x x '>--，利用导数求出函数()g x 的单调区间以及函数的极值，根据单调性、极值判断每个选项，从而可得结论． 【详解】()()xf xg x e =， 则()()()xf x f xg x e '-'=，2x >时，()()0f x f x '->，故()y g x =在(2,)+∞递增，A 正确；2x <时，()()0f x f x '-<，故()y g x =在(,2)-∞递减，故2x =是函数()y g x =的极小值点，故B 正确； 若g （2）0<，则()y g x =有2个零点， 若g （2）0=，则函数()y g x =有1个零点，若g （2）0>，则函数()y g x =没有零点，故D 正确； 由()y g x =在(,2)-∞递减，则()y g x =在(,0)-∞递减， 由0(0)(0)2f g e==，得0x 时，()(0)g x g ， 故()2xf x e，故()2x f x e ≥，故C 错误；故选：C ．【点睛】本题考查了利用导数研究函数的单调性、极值、零点问题，考查了构造函数法的应用，是一道综合题．二､填空题(本大题共4小题，每题5分，共20分.)13. 已知2()2(2)f x x xf '=+，则曲线()y f x =在点(1,(1))f 处的切线方程为________. 【答案】610x y ++= 【解析】 【分析】求出导函数()22(2)f x x f ''=+，令2x =，求出()2f '，从而求出函数表达式以及导函数表达式，求出()1f 以及()1f '，再利用导数的几何意义以及点斜式方程即可求解.【详解】由2()2(2)f x x xf '=+，则()22(2)f x x f ''=+，当2x =时，(2)42(2)f f ''=+，解得()24f '=-，所以2()8f x x x =-，()28f x x '=-，即()17f =-，(1)2186f '=⨯-=-，所以曲线()y f x =在点(1,(1))f 处的切线方程为：()761y x +=--， 即为610x y ++=. 故答案为：610x y ++=【点睛】本题考查了导数的几何意义、基本初等函数的导数以及导数的运算法则，属于基础题.14. 已知()[](]2,0,11,1,x x f x x e x⎧∈⎪=⎨∈⎪⎩(e 为自然对数的底数),则()e 0f x dx =⎰_________.【答案】43【解析】因为()[](]2,0,11,1,x x f x x e x⎧∈⎪=⎨∈⎪⎩，所以()e 1e231e 0101114|ln |33f x dx x dx dx x x x =+=+=⎰⎰⎰ 15. 奇函数()f x 满足(1)(1)f x f x +=-，当01x <≤时，2()log (4)f x x a =+，若1522f ⎛⎫=- ⎪⎝⎭，则()a f a +=__________. 【答案】2 【解析】【分析】根据题中条件，先得到函数的周期，再由21511log (2)2222f f f a ⎛⎫⎛⎫⎛⎫=-=-=-+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭求出a ，进而可求出结果.【详解】由于函数()y f x =为奇函数，且(1)(1)(1)f x f x f x +=-=--，即(2)()f x f x +=-，(4)(2)()f x f x f x ∴+=-+=，所以，函数()y f x =是以4为周期的奇函数，21511log (2)2222f f fa ⎛⎫⎛⎫⎛⎫∴=-=-=-+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，解得2a =. (2)(2)(2)f f f =-=-，(2)0f ∴=.因此，()2(2)2a f a f +=+=. 故答案为：2.【点睛】本题主要考查函数奇偶性与周期性的应用，属于常考题型.16. 定义：如果在函数y ＝f (x )定义域内给定区间[a ，b ]上存在x 0(a ＜x 0＜b )，满足f (x 0)＝()()f b f a b a--，则称函数y ＝f (x )是[a ，b ]上的“平均值函数”，x 0是它的一个均值点，如y ＝x 4是[－1,1]上的平均值函数，0就是它的均值点．现有函数f (x )＝－x 2＋mx ＋1是[－1,1]上的平均值函数，则实数m 的取值范围是________． 【答案】(0,2) 【解析】 【分析】设x 0为均值点，由已知可得：关于x 0的方程(1)(1)1(1)f f ----＝f (x 0)有实数根，整理求得：x 0＝1或x 0＝m －1，结合题意列不等式可得：－1＜m －1＜1，问题得解. 【详解】因为函数f (x )＝－x 2＋mx ＋1是[－1,1]上的平均值函数，设x 0为均值点，所以(1)(1)1(1)f f ----＝m ＝f (x 0)，即关于x 0的方程－20x ＋mx 0＋1＝m 在(－1,1)内有实数根，解方程得x 0＝1或x 0＝m －1. 所以必有－1＜m －1＜1，即0＜m ＜2， 所以实数m 的取值范围是(0,2)．.【点睛】本题主要考查了新概念知识的理解及方程思思，还考查了转化能力及计算能力，属于难题．三､解答题：(本大题共6小题，共70分.解答应写出文字说明､证明过程或演算步骤.)17. 已知函数321()(,)3f x x ax bx a b R =++∈在3x =-处取得极大值9.（1）求a ，b 的值；（2）求函数()f x 在区间[3,3]-上的最值.【答案】(1) 13a b =⎧⎨=-⎩.(2) 函数()f x 在区间[3,3]-上的最大值为9，最小值为53-. 【解析】分析：（I ）首先求解导函数，然后结合()()3039f f ⎧-=⎪⎨-='⎪⎩，可得13a b =⎧⎨=-⎩. （II ）由（I ）得()()()()321-3313f x x x x f x x x '=+∴=+-，结合导函数研究函数的单调性和最值可知函数()f x 在区间[]3,3-上的最大值为9，最小值为53-.详解：（I ）()22f x x ax b =++'依题意得()()3039f f ⎧-=⎪⎨-='⎪⎩， 即9609939a b a b -+=⎧⎨-+-=⎩，解得13a b =⎧⎨=-⎩.经检验，上述结果满足题意. （II ）由（I ）得()()()()3221-323=313f x x x x f x x x x x =+∴'=+-+-， 令()0f x '>，得31x x -或；令()0f x '<，得31x -<<，()f x ∴的单调递增区间为()1+∞，和()--3∞，，()f x 的单调递增区间是()-3,1，()()=39f x f ∴-=极大值，()()()5=1,393f x f f =-=极小值又，所以函数()f x 在区间[]3,3-上的最大值为9，最小值为53-.点睛：(1)可导函数y ＝f (x )在点x 0处取得极值的充要条件是f ′(x 0)＝0，且在x 0左侧与右侧f ′(x )的符号不同．(2)若f (x )在(a ，b )内有极值，那么f (x )在(a ，b )内绝不是单调函数，即在某区间上单调增或减的函数没有极值．18. 对于函数()()()212,0f x ax b x b a =+++-≠,若存在实数0x ,使()0f x =0x 成立,则称0x 为()f x 的不动点.（1）当2,2a b ==-时,求()f x 的不动点；（2）若对于任意实数b ,函数()f x 恒有两个不相同的不动点,求a 的取值范围 【答案】（1）1-和2；（2）（0,2） 【解析】 【分析】（1）把a ，b 的值代入方程，解出方程22240x x --=即可得()f x 的不动点；（2）根据方程有两解可得2480b ab a -+>，将其看成关于b 的二次函数，根据10∆<即可得结果. 【详解】⑴由题义()()222122x x x +-++--=整理得22240x x --=,解方程得121,2x x =-= 即()f x 的不动点为-1和2．⑵由()f x =x 得220ax bx b ++-=如此方程有两解,则有△=()2242480b a b b ab a --=-+>把2480b ab a -+>看作是关于b 的二次函数,则有1∆=()()()2244816321620a a a a a a -=-=-<，解得02a <<即为所求.【点睛】本题主要考查了二次函数的性质，考查了新定义问题，考查了转化思想，将“b ”看成自变量是解题的关键，是一道中档题．19. 某市近郊有一块大约500500m m ⨯的接近正方形的荒地，地方政府准备在此建一个综合性休闲广场，首先要建设如图所示的一个矩形场地，其中总面积为3000平方米，其中阴影部分为通道，通道宽度为2米，中间的三个矩形区域将铺设塑胶地面作为运动场地（其中两个小场地形状相同），塑胶运动场地占地面积为S 平方米． （1）分别用x 表示y 和S 的函数关系式，并给出定义域； （2）怎样设计能使S 取得最大值，并求出最大值．【答案】（1）1500030306S x x ⎛⎫=-+⎪⎝⎭，其定义域是(6,500)． （2）设计50x m =，60y m =时，运动场地面积最大，最大值为2430平方米． 【解析】 【分析】（1）总面积为3000xy =，且26a y +=，则3000y x=，1500332y a x =-=-（其中6500)x <<，从而运动场占地面积为(4)(6)S x a x a =-+-，代入整理即得； （2）由（1）知，占地面积1500015000303063030(6)S x x x x=--=-+，由基本不等式可得函数的最大值，以及对应的x 的值． 【详解】解：（1）由已知3000xy =，∴3000y x=，其定义域是(6,500)．(4)(6)(210)S x a x a x a =-+-=-， 26a y +=，∴1500332y a x=-=-， ∴150015000(210)(3)3030(6)S x x x x=--=-+，其定义域是(6,500)． （2）150003030(6)3030303023002430S x x x x=-+-=-⨯=， 当且仅当150006x x=，即50(6,500)x =∈时，上述不等式等号成立， 此时，50x =，60y =，2430max S =．答：设计50x m =，60y m =时，运动场地面积最大，最大值为2430平方米．【点睛】本题以实际问题为载体，考查函数模型的构建，考查应用基本不等式求函数最值，构建函数关系式是关键，属于中档题．20. 已知函数f （x ）=2sin x －x cos x －x ，f′（x ）为f （x ）的导数．（1）证明：f′（x ）在区间（0，π）存在唯一零点； （2）若x ∈[0，π]时，f （x ）≥ax ，求a 的取值范围． 【答案】（1）见解析； （2）(],0a ∈-∞. 【解析】 【分析】（1）求导得到导函数后，设为()g x 进行再次求导，可判断出当0,2x π⎛⎫∈ ⎪⎝⎭时，()0g x '>，当,2x ππ⎛⎫∈⎪⎝⎭时，()0g x '<，从而得到()g x 单调性，由零点存在定理可判断出唯一零点所处的位置，证得结论；（2）构造函数()()h x f x ax =-，通过二次求导可判断出()()min 2h x h a π''==--，()max 222h x h a ππ-⎛⎫''==- ⎪⎝⎭；分别在2a ≤-，20a -<≤，202a π-<<和22a π-≥的情况下根据导函数的符号判断()h x 单调性，从而确定()0h x ≥恒成立时a 的取值范围.【详解】（1）()2cos cos sin 1cos sin 1f x x x x x x x x '=-+-=+-令()cos sin 1g x x x x =+-，则()sin sin cos cos g x x x x x x x '=-++= 当()0,x π∈时，令()0g x '=，解得：2x π=∴当0,2x π⎛⎫∈ ⎪⎝⎭时，()0g x '>；当,2x ππ⎛⎫∈ ⎪⎝⎭时，()0g x '<()g x ∴在0,2π⎛⎫ ⎪⎝⎭上单调递增；在,2ππ⎛⎫⎪⎝⎭上单调递减又()0110g =-=，1022g ππ⎛⎫=->⎪⎝⎭，()112g π=--=- 即当0,2x π⎛⎫∈ ⎪⎝⎭时，()0g x >，此时()g x 无零点，即()f x '无零点 ()02g g ππ⎛⎫⋅< ⎪⎝⎭ 0,2x ππ⎛⎫∴∃∈ ⎪⎝⎭，使得()00g x = 又()g x 在,2ππ⎛⎫⎪⎝⎭上单调递减 0x x ∴=为()g x ，即()f x '在,2ππ⎛⎫⎪⎝⎭上的唯一零点 综上所述：()f x '在区间()0,π存在唯一零点（2）若[]0,x π∈时，()f x ax ≥，即()0f x ax -≥恒成立 令()()()2sin cos 1h x f x ax x x x a x =-=--+ 则()cos sin 1h x x x x a '=+--，()()cos h x x x g x '''== 由（1）可知，()h x '在0,2π⎛⎫⎪⎝⎭上单调递增；在,2ππ⎛⎫⎪⎝⎭上单调递减 且()0h a '=-，222h a ππ-⎛⎫'=-⎪⎝⎭，()2h a π'=-- ()()min 2h x h a π''∴==--，()max 222h x h a ππ-⎛⎫''==- ⎪⎝⎭①当2a ≤-时，()()min 20h x h a π''==--≥，即()0h x '≥在[]0,π上恒成立()h x ∴在[]0,π上单调递增()()00h x h ∴≥=，即()0f x ax -≥，此时()f x ax ≥恒成立②当20a -<≤时，()00h '≥，02h π⎛⎫'>⎪⎝⎭，()0h π'< 1,2x ππ⎛⎫∴∃∈ ⎪⎝⎭，使得()10h x '=()h x ∴在[)10,x 上单调递增，在(]1,x π上单调递减又()00h =，()()2sin cos 10h a a ππππππ=--+=-≥()0h x ∴≥在[]0,π上恒成立，即()f x ax ≥恒成立③当202a π-<<时，()00h '<，2022h a ππ-⎛⎫'=->⎪⎝⎭20,2x π⎛⎫∴∃∈ ⎪⎝⎭，使得()20h x '=()h x ∴在[)20,x 上单调递减，在2,2x π⎛⎫⎪⎝⎭上单调递增()20,x x ∴∈时，()()00h x h <=，可知()f x ax ≥不恒成立④当22a π-≥时，()max 2022h x h a ππ-⎛⎫''==-≤⎪⎝⎭()h x ∴在0,2π⎛⎫⎪⎝⎭上单调递减00h x h可知()f x ax ≥不恒成立 综上所述：(],0a ∈-∞【点睛】本题考查利用导数讨论函数零点个数、根据恒成立的不等式求解参数范围的问题.对于此类端点值恰为恒成立不等式取等的值的问题，通常采用构造函数的方式，将问题转变成函数最值与零之间的比较，进而通过导函数的正负来确定所构造函数的单调性，从而得到最值.21. 已知函数f (x )＝e x (e x －a )－a 2x ，其中参数a ≤0. (1)讨论f (x )的单调性； (2)若f (x )≥0，求a 的取值范围.【答案】(1) f (x )在,ln 2⎛⎫⎛⎫-∞-⎪ ⎪⎝⎭⎝⎭a 上单调递减，在区间ln ,2⎛⎫⎛⎫-+∞ ⎪ ⎪⎝⎭⎝⎭a 上单调递增.【解析】 【分析】(1)求f (x )的导函数为f ′(x )＝(2e x ＋a )(e x －a )，通过讨论a ，求函数的单调区间即可. (2)因为f (x )≥0，所以即求f (x )的最小值大于等于0，由第(1)的结果求的f (x )的最小值，解关于a 的不等式即可求出a 的范围.【详解】(1)函数f (x )的定义域为(－∞，＋∞)，且a ≤0. f ′(x )＝2e 2x －a e x －a 2＝(2e x ＋a )(e x －a ).①若a ＝0，则f (x )＝e 2x ，在(－∞，＋∞)上单调递增. ②若a <0，则由f ′(x )＝0，得x ＝ln 2a ⎛⎫-⎪⎝⎭. 当x ∈,ln 2⎛⎫⎛⎫-∞-⎪ ⎪⎝⎭⎝⎭a 时，f ′(x )<0； 当x ∈ln ,2⎛⎫⎛⎫-+∞ ⎪ ⎪⎝⎭⎝⎭a 时，f ′(x )>0. 故f (x )在,ln 2⎛⎫⎛⎫-∞-⎪ ⎪⎝⎭⎝⎭a 上单调递减，在区间ln ,2⎛⎫⎛⎫-+∞ ⎪ ⎪⎝⎭⎝⎭a 上单调递增.(2)①当a ＝0时，f (x )＝e 2x ≥0恒成立. ②若a <0，则由(1)得，当x ＝ln 2a ⎛⎫-⎪⎝⎭时，f (x )取得最小值，最小值为f ln 2a ⎛⎫⎛⎫- ⎪⎪⎝⎭⎝⎭＝a 23ln 42a ⎡⎤⎛⎫--⎪⎢⎥⎝⎭⎣⎦， 故当且仅当a 23ln 42a ⎡⎤⎛⎫--⎪⎢⎥⎝⎭⎣⎦≥0， 即0>a ≥342e -时，f (x )≥0. 综上a 的取值范围是[342e -，0].【点睛】本题考查利用导数求函数的单调区间，考查函数的恒成立问题，同时考查了分类讨论的思想和学生的计算能力，属于中档题.22. 若以直角坐标系xOy 的O 为极点，Ox 为极轴，选择相同的长度单位建立极坐标系，得曲线的极坐标方程是26cos sin θρθ=. （1）将曲线C 的极坐标方程化为直角坐标方程，并指出曲线是什么曲线；（2）若直线l的参数方程为32x t y ⎧=+⎪⎨⎪=⎩(t 为参数)，3,02P ⎛⎫⎪⎝⎭，当直线l 与曲线C 相交于A ，B两点，求2||||||AB PA PB ⋅. 【答案】（1）曲线C 的直角坐标系方程为26y x =，曲线为以3,02⎛⎫⎪⎝⎭为焦点，开口向右的抛物线；（2）163. 【解析】 【分析】（1）运用极坐标与直角坐标之间的关系将曲线C 的极坐标方程26cos sin θρθ=化为直角坐标方程，再依据圆锥曲线的标准方程的特征进行判断；（2）将直线的参数方程32x t y ⎧=+⎪⎨⎪=⎩代入曲线方程26y x =，运用直线参数方程中的参数t 的几何意义进行求解. 【详解】（1）∵26cos sin θρθ=，∴22sin 6cos ρθρθ=， ∴曲线C 的直角坐标系方程为26y x =，曲线为以3,02⎛⎫⎪⎝⎭为焦点，开口向右的抛物线. （2）直线l的参数方程可化为31222x t y t ⎧=+⎪⎪⎨⎪=⎪⎩，代入26y x =得24120t t --=.则12124,12t t t t +==-，128AB t t =-==，因为3,02P ⎛⎫⎪⎝⎭在直线l 上，所以1212PA PB t t ，∴2||6416||||123AB PA PB ==⋅. 【点睛】本题关键点是熟练掌握极坐标方程和普通方程的转化公式；熟练利用直线参数方程中的参数t 的几何意义进行求解. 23. 设,,x y z ∈R ，且1x y z ++=.（1）求222(1)(1)(1)x y z -++++的最小值； （2）若2221(2)(1)()3x y z a -+-+-≥成立，证明：3a ≤-或1a ≥-. 【答案】(1) 43；(2)见详解. 【解析】 【分析】(1)根据条件1x y z ++=，和柯西不等式得到2224(1)(1)(1)3x y z -++++≥，再讨论,,x y z 是否可以达到等号成立的条件.(2)恒成立问题，柯西不等式等号成立时构造的,,x y z 代入原不等式，便可得到参数a 的取值范围. 【详解】(1)22222222[(1)(1)(1)](111)[(1)(1)(1)](1)4x y z x y z x y z -++++++≥-++++=+++=故2224(1)(1)(1)3x y z -++++≥等号成立当且仅当111x y z -=+=+而又因1x y z ++=，解得531313x y z ⎧=⎪⎪⎪=-⎨⎪⎪=-⎪⎩时等号成立所以222(1)(1)(1)x y z -++++的最小值为43. (2)因为2221(2)(1)()3x y z a -+-+-≥，所以222222[(2)(1)()](111)1x y z a -+-+-++≥.根据柯西不等式等号成立条件，当21x y z a -=-=-，即22321323a x a y a z a +⎧=-⎪⎪+⎪=-⎨⎪+⎪=-⎪⎩时有22222222[(2)(1)()](111)(21)(2)x y z a x y z a a -+-+-++=-+-+-=+成立.所以2(2)1a +≥成立，所以有3a ≤-或1a ≥-.【点睛】两个问都是考查柯西不等式，属于柯西不等式的常见题型.。

某某某某市五原中学补习部2021届高三数学上学期期中试题 文（含解析）第Ⅰ卷（共60分）一.选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. “若1sin 2x ≥，则6x π≥”的否命题是（） A. 若1sin 2x ，则6x π< B. 若6x π≥，则1sin 2x ≥ C. 若6x π<，则1sin 2x D. 若1sin 2x ≤，则6x π≤ 【答案】A【解析】【分析】 否命题就是把条件和结论都否定，写出结论即可.【详解】“若1sin 2x ≥，则6x π≥”的否命题是“若1sin 2x ，则6x π<” 故选：A.【点睛】易错点睛：否命题与命题的否定有一定的区别：（1）否命题需否定原命题的条件和结论；（2）命题的否定只需直接否定结论即可.2. “f (x )为偶函数”是“()22x x f x -=+”的（） A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】B【解析】【分析】利用定义判断()22x xf x -=+是偶函数，再利用充分必要性的定义判断，即可得出答案. 【详解】()22x x f x -=+，定义域为R ，()22()x x f x f x --=+=()f x ∴是定义在R 上的偶函数，故必要性成立；但若()f x 为偶函数，()f x 表达式不唯一，举反例：2()f x x =，()2x f x =，等等，不能推出()22x x f x -=+，故充分性不成立；所以“()f x 为偶函数”是“()22x x f x -=+”的必要不充分条件.故选：B.3. 如图所示，I 是全集，,,M P S 是I 的三个子集，则阴影部分所表示的集合是（）A. ()M P SB. ()MP S C. ()()I M S P ⋂⋂D. ()()I M S P ⋂⋃【答案】C【解析】【分析】 根据阴影部分与对应集合关系可直接判断得结果.【详解】由图可知：阴影部分中元素在集合M 中、且在集合P 中、且不在集合S 中,即在集合I S 中,因此阴影部分表示的集合为()()IM P S 故选：C【点睛】本题考查韦恩图、元素与集合关系，考查基本分析判断能力，属基础题.4. 已知tan 2θ=，则2sin sin cos 2θθθ+-=（） A. 35B. 45C. 54D. 45- 【答案】D【解析】【分析】利用三角函数平方关系化简整理得：原式22sin sin cos 2cos θθθθ=-+-变形处理2222sin sin cos 2cos sin +cos θθθθθθ-+-=，分子分母同时除以2cos θ，即可得解. 【详解】因为22sin +cos 1θθ=，sin tan cos θθθ= 所以222sin sin cos 2sin sin cos 2cos θθθθθθθ+-=-+-222222sin sin cos 2cos tan tan 2sin +cos tan +1θθθθθθθθθ-+--+-== 42244+15-+-==- 故选：D.5. 已知α是第二象限角，5tan 12α=-，则cos α=（） A. 1213B. 1213- C. 513D. 513- 【答案】B【解析】【分析】先由α是第二象限角，得cos 0α<；再由同角三角函数基本关系求解，即可得出结果.【详解】因为α是第二象限角，所以cos 0α<， 又5tan 12α=-，所以22sin 5cos 12sin cos 1αααα⎧=-⎪⎨⎪+=⎩，因此2225cos cos 1144αα+=， 即2144cos 169α=，所以12cos 13α=-. 故选：B.6. 函数()ln x f x x=，若(4)a f =，(5.3)b f =，(6.2)c f =，则（） A a b c << B. c b a << C. c a b << D. b a c <<【答案】B【解析】【分析】 求导'21ln ()x f x x-=，可得()f x 在(,)e +∞的单调性，利用单调性，即可得答案. 【详解】因为()ln x f x x=(0)x >， 所以'21ln ()x f x x -=， 当x e >时，'()0f x <，则()f x 在(,)e +∞为减函数，因为4 5.3 6.2e <<<，所以(4)(5.3)(6.2)f f f >>，即a b c >>，故选：B7. 已知4sin()35ππα++=，则cos()6πα-=（） A. 45B. 45- C. 35D. 35 【答案】B【解析】【分析】先利用诱导公式化简题目得到4sin()35πα+=-，再由632πππαα-=+-，利用诱导公式，得cos()sin(+)63ππαα-=，即可求解得到答案. 【详解】由题意，4sin()sin()335πππαα++=-+=，即4sin()35πα+=- 又632πππαα-=+-，利用三角函数的诱导公式可得：4cos()cos()sin(+)63235ππππααα-=+-==- 故选：B. 【点睛】方法点睛：三角函数化简求值，常用拼凑角：（1）再利用诱导公式求值或化简时，巧用相关角的关系会简化解题过程，常见的互余关系有：3πα+与6πα-，3πα-与6πα+，4πα-与4απ+等；常见的互补关系有：3πα+与23πα-，4πα+与34πα-等； （2）在利用两角和与差的三角函数公式求值或化简时，常根据角与角之间的和差、倍半、互余、互补的关系，运用角的变换，沟通条件与结论的差异，使问题获解，常见角的变换方式有：()ααββ=+-，2()()ααβαβ=++-，2()αβααβ-=+-等.8. 函数()()sin ln 2x f x x =+的部分图象可能是（ ） A. B.C. D.【答案】A【解析】【分析】考查函数()y f x =的定义域、在()1,0-上的函数值符号，可得出正确选项.【详解】对于函数()y f x =，2021x x +>⎧⎨+≠⎩，解得2x >-且1x ≠-， 该函数的定义域为()()2,11,---+∞，排除B 、D 选项.当10x -<<时，sin 0x <，122x <+<，则()ln 20x +>，此时，()()sin 0ln 2x f x x =<+， 故选A.【点睛】本题考查函数图象的识别，一般从函数的定义域、奇偶性、单调性、零点、函数值符号进行判断，考查分析问题和解决问题的能力，属于中等题.9. 若()()2log ,021,02x x x f x x ⎧-<⎪+=⎨⎛⎫≥⎪ ⎪⎝⎭⎩，则2(2)(log 12)f f -+=（） A. 112B. 2C. 3D. 73 【答案】D【解析】【分析】令22x +=-和22log 12x +=，分别解得4x =-和2log 3x =，代入对应的解析式，即可得答案.【详解】令4x =-，因为40-<，则2log (22)4f -==，令2log 30x =>，则222log 3log 12+=， 所以21log 32log 3211(log 12)()223f -===，所以2(2)(log 12)f f -+=17233+=， 故选：D 10. 已知函数()37sin f x x x x =--+，若()()220f a f a +->，则实数a 的取值X 围是 A. (),1-∞ B. (),3-∞ C. ()1,2- D. ()2,1-【答案】D【解析】【分析】先研究函数()f x 奇偶性与单调性，再根据奇偶性与单调性化简不等式()()220f a f a +->，解得实数a 的取值X 围.【详解】因为()()37sin ,f x x x x f x -=+-=-2()37cos 0f x x x =--+<' , 所以()f x 为奇函数，且在R 上单调递减，因为()()220f a f a +->，所以()()()2222,2,21f a f a f a a a a >--=-<--<<，选D.【点睛】解函数不等式：首先根据函数的性质把不等式转化为(())(())f g x f h x >的形式，然后根据函数的单调性去掉“f ”，转化为具体的不等式(组)，此时要注意()g x 与()h x 的取值应在外层函数的定义域内.11. 已知函数21,2()3, 2.1x x f x x x ⎧-<⎪=⎨≥⎪-⎩若方程()0f x a -=有三个不同的实数根，则实数a 的取值X 围为（）A. (0,1)B. (0,2)C. (0,3)D. (1,3)【答案】A【解析】【分析】根据函数()f x的解析式，作出函数()f x的图象，方程()0f x a-=有三个不同的实数根即为函数()y f x=的图象与y a=的图象有三个不同的交点，结合函数的图象即可求得实数a 的取值X围.【详解】21,2()3,21x xf xxx⎧-<⎪=⎨≥⎪-⎩，∴图象如图：方程()0f x a-=有三个不同的实数根即为函数()y f x=的图象与y a=的图象有三个不同的交点，由图象可知：a的取值X围为(0,1).故选：A【点睛】本题主要考查了分段函数的应用，考查了分段函数的图象，函数与方程的关系，考查了数形结合与转化化归的思想.12. 已知函数()f x的导函数为()f x'，且()()f x f x'<对任意的x∈R恒成立，则下列不等式均成立的是（）A. ()()()()2ln220,20f f f e f<< B. ()()()()2ln220,20f f f e f>>C. ()()()()2ln220,20f f f e f<> D. ()()()()2ln220,20f f f e f><【答案】A【解析】【分析】构造函数()()x f x g x e=，求出函数()g x 的导数，判断函数的单调性，从而求出结果. 【详解】令()()x f x g x e =，则2()()()()()x x x xe f x e f x f x f x g x e e '--='='. ()()f x f x '<，∴()0g x '<，∴()g x 是减函数，则有(ln 2)(0)g g <，(2)(0)g g <，即ln 2020(ln 2)(0)(2)(0),f f f f e e e e<<，所以2(ln 2)2(0),(2)(0)f f f e f <<.选A . 【点睛】本题考查函数与导数中利用函数单调性比较大小.其中构造函数是解题的难点.一般可通过题设已知条件结合选项进行构造.对考生综合能力要求较高.第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题卡上）13. 计算sin()24ππ+=_______;【解析】【分析】利用诱导公式以及三角函数值即可求解.【详解】sin()cos 2442πππ+==.故答案：214. 若lg 2lg21a -=，则a =______ ;【答案】40【解析】【分析】利用对数的运算公式log log n a a n M M =，log log log ()a a a M N MN +=，直接求值即可.【详解】lg 2lg 21a -=lg 2lg 21lg 4lg10lg 40a ∴=+=+=40a ∴=故答案为：4015. 已知函数3()1f x x ax =--在()1,+∞内为增函数，则a 的取值X 围；____ ； .【答案】3a ≤【解析】【分析】求出导函数使2()30f x x a '=-≥在()1,+∞恒成立即可求解,【详解】由3()1f x x ax =--，则2()3f x x a '=-因为函数在()1,+∞内为增函数，则2()30f x x a '=-≥在()1,+∞恒成立， 即23a x ≤在()1,+∞恒成立，所以3a ≤.故答案为：3a ≤16. 若12,x x 是函数2()74ln f x x x x =-+的两个极值点，则12x x =____，12()()f x f x +=____.【答案】 (1). 2 (2). 654ln 24-【解析】【分析】根据极值点定义，即可由方程的根与系数之间的关系，即可求得12x x 以及12x x +，再结合对数运算即可容易求得结果.【详解】2121247()2702740,22f x x x x x x x x x '=-+=⇒-+=⇒+==，2212111222()()74ln 74ln f x f x x x x x x x +=-++-+21212121265()27()4ln()4ln 24x x x x x x x x =+--++=-.故答案为：2；654ln 24-. 【点睛】本题考查利用导数求函数的极值点，涉及对数运算，属综合基础题.三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） 17. 已知角α的顶点与原点O 重合，始边与x 轴的非负半轴重合，它的终边在直线430x y -=上.（1）求sin()απ+的值；（2）求2sin cos sin cos 1tan ααααα+--值． 【答案】（1）45-或45；（2）75-或75； 【解析】 【分析】（1）在直线430x y -=上任取一点4(,)3P m m (0)m ≠，由已知角α的终边过点4(,)3P m m ，利用诱导公式与三角函数定义即可求解，要注意分类讨论m 的正负.（2）先利用商的关系化简原式为sin cos αα+，结合第一问利用三角函数定义分别求得cos α与sin α，要注意分类讨论m 的正负.【详解】（1）在直线430x y -=上任取一点4(,)3P m m (0)m ≠，由已知角α的终边过点4(,)3P m m ，x m ∴=，43y m =，224533r OP m m m ⎛⎫==+= ⎪⎝⎭利用诱导公式与三角函数定义可得：sin()sin 443553mm m m απα=-=-+=-，当0m >时，4in()5s απ-+=；当0m <时，4sin()5απ+=（2）原式22222sin cos sin cos sin cos sin sin cos sin cos cos sin sin cos 1cos αααααααααααααααα-=+=+=-----()()sin cos sin cos sin cos sin cos αααααααα+-==+-同理（1）利用三角函数定义可得：3553cos m mm m α==， 当0m >时，4sin 5α，3cos 5α=，此时原式75=；当0m <时，4sin 5α=-，3cos 5α=-，此时原式75=-；【点睛】易错点睛：本题考查三角函数化简求值，解本题时要注意的事项：角α的终边在直线430x y -=上，但未确定在象限，要分类讨论，考查学生的转化能力与运算解能力，属于中档题.18. 已知函数321()(,)3f x x ax bx a b R =++∈在3x =-处取得极大值为9. （1）求a ，b 的值；（2）求函数()f x 在区间[3,3]-上的最值.【答案】(1) 13a b =⎧⎨=-⎩.(2) 函数()f x 在区间[3,3]-上的最大值为9，最小值为53-. 【解析】分析：（I ）首先求解导函数，然后结合()()3039f f ⎧-=⎪⎨-='⎪⎩，可得13a b =⎧⎨=-⎩.（II ）由（I ）得()()()()321-3313f x x x x f x x x '=+∴=+-，结合导函数研究函数的单调性和最值可知函数()f x 在区间[]3,3-上的最大值为9，最小值为53-.详解：（I ）()22f x x ax b =++'依题意得()()3039f f ⎧-=⎪⎨-='⎪⎩，即9609939a b a b -+=⎧⎨-+-=⎩，解得13a b =⎧⎨=-⎩.经检验，上述结果满足题意.（II ）由（I ）得()()()()3221-323=313f x x x x f x x x x x =+∴'=+-+-， 令()0f x '>，得31x x -或；令()0f x '<，得31x -<<，()f x ∴的单调递增区间为()1+∞，和()--3∞，，()f x 的单调递增区间是()-3,1，()()=39f x f ∴-=极大值，()()()5=1,393f x f f =-=极小值又，所以函数()f x 在区间[]3,3-上的最大值为9，最小值为53-.点睛：(1)可导函数y ＝f (x )在点x 0处取得极值的充要条件是f ′(x 0)＝0，且在x 0左侧与右侧f ′(x )的符号不同．(2)若f (x )在(a ，b )内有极值，那么f (x )在(a ，b )内绝不是单调函数，即在某区间上单调增或减的函数没有极值．19. 如图，在直角坐标系xOy 中，角α的顶点是原点，始边与轴正半轴重合，终边交单位圆于点A ，且,62ππα⎛⎫∈⎪⎝⎭，将角α的终边按照逆时针方向旋转3π，交单位圆于点B ，记()()1122,,,A x y B x y（1）若113x =，求2x ； （2）分别过A 、B 做x 轴的垂线，垂足依次为C 、D ，记AOC ∆的面积为1S ，BOD ∆的面积为2S ，若122S S =，求角α的值.【答案】（1）2x =；（2）4πα=【解析】 【分析】（1）由三角函数定义，得11cos 3x α==，由此利用同角三角函数的基本关系求得sin α的值，再根据2cos()3x πα=+，利用两角和的余弦公式求得结果．（2）依题意得1sin y α=，2sin()3y πα=+，分别求得1S 和2S 的解析式，再由122S S =求得cos 20α=，根据α的X 围，求得α的值．【详解】（1）解：由三角函数定义，得1cos x α=，2cos()3x πα=+．因为(,)62ππα∈，1cos 3α=，所以sin α==．所以21cos()cos 32x π=+==αα-α． （2）解：依题意得1sin y α=，2sin()3y πα=+．所以111111cos sin sin 2224S x y ααα===，2221112||[cos()]sin()sin(2)223343S x y πππααα==-++=-+． 依题意122S S =得2sin 22sin(2)3παα=-+，即22sin 22[sin 2coscos2sin ]sin 233ππααααα=-+=， 整理得cos 20α=． 因为62ππα<<，所以23παπ<<，所以22πα=，即4πα=．【点睛】本题主要考查任意角的三角函数的定义，两角和差的正弦公式、余弦公式，同角三角函数的基本关系的应用，属于中档题．20. 已知函数f(x)＝ln x－ax(a∈R).（1）当a＝12时，求f(x)的极值；（2）讨论函数f(x)在定义域内极值点的个数.【答案】（1）f(x)极大值＝ln2－1，无极小值；（2）答案见解析.【解析】【分析】（1）当a＝12时，f(x)＝ln x－12x，求导得到f′(x)＝1x－12＝22xx-，然后利用极值的定义求解.（2）由（1）知，函数的定义域为(0，＋∞)，f′(x)＝1x －a＝1axx-(x>0)，然后分a≤0和a>0两种情况讨论求解.【详解】（1）当a＝12时，f(x)＝ln x－12x，函数的定义域为(0，＋∞)且f′(x)＝1x－12＝22xx-，令f′(x)＝0，得x＝2，于是当x变化时，f′(x)，f(x)的变化情况如下表.x (0，2) 2 (2，＋∞) f′(x) ＋0 －f (x )ln2－1故f (x )在定义域上的极大值为f (x )极大值＝f (2)＝ln2－1，无极小值. （2）由（1）知，函数的定义域为(0，＋∞)，f ′(x )＝1x －a ＝1ax x- (x >0) 当a ≤0时，f ′(x )>0在(0，＋∞)上恒成立，即函数在(0，＋∞)上单调递增，此时函数在定义域上无极值点； 当a >0时，当x ∈10,a ⎛⎫⎪⎝⎭时，f ′(x )>0， 当x ∈1,a ⎛⎫+∞⎪⎝⎭时，f ′(x )<0， 故函数在x ＝1a处有极大值. 综上可知，当a ≤0时，函数f (x )无极值点， 当a >0时，函数y ＝f (x )有一个极大值点，且为x ＝1a. 【点睛】本题主要考查导数与函数极值以及极值点的个数问题，还考查了分类讨论的思想和运算求解的能力，属于中档题. 21. 已知函数21()(1)ln 2f x x ax a x =-+-；（1）若12a <≤，求函数()f x 的单调递减区间； （2）求证：若15a <<，则对任意的120x x >>，有1212()()1f x f x x x ->--．【答案】（1）{}|11x a x -<<；（2）证明见解析.【解析】【分析】（1）求出()f x 的导函数，根据12a <≤可得到单调递减区间； （2）令21()()(1)ln 2g x f x x x ax a x x =+=-+-+()0x >，判断出单调性，利用12()()g x g x >可得答案.【详解】（1）21()(1)ln 2f x x ax a x =-+-的定义域为(0+)∞，， [](1)(1)1()x x a a f x x a x x----'=-+=， 因为12a <≤，所以011a <-≤，当11a -=即2a =时，()f x 在(0+)∞，单调递增， 当011a <-<时，即02a <<，令()0f x '<得11a x -<<，所以()f x 单调递减， 单调递减区间为{}|11x a x -<<，综上所述，2a =时，()f x 无单调递减区间；02a <<时，()f x 单调递减区间为{}|11x a x -<<.（2）设21()()(1)ln 2g x f x x x ax a x x =+=-+-+()0x >，则 21(1)1()1a x a x a g x x a x x-+-+-'=-++=， 令2()(1)1M x x a x a =+-+-，所以2(1)4(1)(1)(5)a a a a ∆=---=--， 因为15a <<，所以(1)(5)0a a ∆=--<，所以()0M x >，即()0g x '>， 所以()g x 在(0+)∞，上单调递增， 对任意的120x x >>，有12()()g x g x >，即1122()()f x x f x x +>+，1212()()()f x f x x x ->--，所以1212()()1f x f x x x ->--.【点睛】利用导数()0f x '<求得函数的单调递减区间，利用导数()0f x '>求得函数的单调递增区间.选做题：共10分.请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分. 【选修4-4：坐标系与参数方程】22. 已知曲线C 的极坐标方程是2cos ρθ=，若以极点为平面直角坐标系的原点，极轴为x 轴的正半轴，且取相同的单位长度建立平面直角坐标系，则直线l的参数方程是12x m y t ⎧=+⎪⎪⎨⎪=⎪⎩（t 为参数）．（1）求曲线C 的直角坐标方程与直线l 的普通方程；（2）设点(),0P m ，若直线l 与曲线C 交于,A B 两点，且1PA PB ⋅=，求非负实数m 的值． 【答案】（1）曲线C 的直角坐标方程为()2211x y -+=，直线l 的普通方程为0x m -=；（2）1m =或1m = 【解析】 【分析】（1）2cos ρθ=得22cos ρρθ=，结合cos sin x y ρθρθ=⎧⎨=⎩即可求出曲线C 的直角坐标方程，由12yt 得2t y ，代入到3xt m 可得直线l 的普通方程； （2）将直线l 的参数方程代入到曲线C 的直角坐标方程，利用韦达定理和参数的几何意义即可求出答案．【详解】解：（1）∵曲线C 的极坐标方程是2cos ρθ=，即22cos ρρθ=，由cos sin x y ρθρθ=⎧⎨=⎩得222x y x +=，即曲线C 的直角坐标方程为()2211x y -+=，由12yt 得2t y ，代入到3xt m 可得， 直线l 的普通方程为0x m -=；（2）将12x m y t ⎧=+⎪⎪⎨⎪=⎪⎩代入到222x y x +=得，可得223120t m t m m ， 由2231420m m m可得13m -<<，由m 为非负数，可得03m ≤<， 设12,t t 是方程的两根，则2122t t m m ，由1PA PB ⋅=可得21221t t m m，解得1m =或12m ，又03m ≤<，∴1m =或1m =+【点睛】本题主要考查参数方程与普通方程的互化，考查极坐标方程与直角坐标方程的互化，考查直线的参数方程中参数的几何意义，属于中档题．选修4-5：不等式选讲23. 已知f (x )＝|2x －1|＋2|x ＋1| （1）求函数f (x )的最小值；（2）若f (x )的值域为M ，当t ∈M 时，证明t 2＋1≥3t＋3t . 【答案】（1）()min 3f x =；（2）证明见详解. 【解析】 【分析】（1）利用绝对值三角不等式即可求解. （2）利用作差法即可证明.【详解】（1）()2121f x x x =-++212221223x x x x =-++≥---=，当且仅当()()21220x x -+≤时，取等号，()min 3f x ∴=.（2）由（1）可得[)3,M =+∞， 原不等式等价于32233313t t t t t t t-+-+--=()()231t t t-+=t M ∈，30t ∴-≥，210t +>，()()2310t t t-+∴≥，∴ t 2＋1≥3t＋3t .【点睛】方法点睛：本题考查了分段函数的最值、证明不等式，常见方法有以下几种. （1）去绝对值，将函数化为分段函数，利用分段函数的图像可求最值. （2）利用绝对值三角不等式求最值. （3）证明不等式的方法：作差法、作商法. （4）构造函数，利用导函数证明不等式.。

2021年高三上学期期中检测数学（文）试卷含答案本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试用时120分钟。

第Ⅰ卷1至2页，第Ⅱ卷3至6页。

答卷前，考生务必将自己的姓名、准考号填写在答题卡上，并在规定位置粘贴考试用条形码。

答题时，务必将答案涂写在答题卡上，答在试卷上的无效。

考试结束后，将本试卷和答题卡一并交回。

祝各位考生考试顺利！第Ⅰ卷注意事项：1．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

2．本卷共8题，共40分。

一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．（1）已知集合，，则集合（A）（B）（C）（D）（2）是虚数单位，复数=（A）（B）（C）（D）（3）命题“对”的否定是（A）（B）（C）（D）（4）某程序框图如右图所示，则输出的结果S等于（A ） （B ） （C ） （D ）（5）设0.30.33log 2,log 2,2,a b c ===则这三个数的大小关系是（ ）（A ） （B ） （C ） （D ）（6）已知，，，若，则（A ） （B ） （C ） （D ）（7）函数图象上各点的横坐标缩短到原来的倍（纵坐标不变），右平移个单位，那么所得图象的一条对称轴方程为（A ） （B ） （C ） （D ）（8）如图，在三角形中，已知，，，点为的三等分点．则的取值范围为 （A ） （B ） （C ） （D ）第Ⅱ卷注意事项：1．用黑色墨水的钢笔或签字笔将答案写在答题卡上．．．．．．．．．。

2．本卷共12题，共110分。

二、填空题：本大题共6个小题，每小题5分，共30分． （9）设全集，集合，，则 ． （10） ． （11）计算：2log 151log 25lg2100++= ． 第（8）题图CDBA第14题图（12）在中， ，，，则的面积等于____. （13）设函数，则的值是________．（14）如图，△为圆的内接三角形，为圆的弦， 且． 过点作圆的切线与的延长线交于点， 与交于点．若，，则线段的长为 .三、解答题：本大题共6小题，共80分．解答应写出文字说明、证明过程或演算步骤． （15）（本小题满分13分）已知集合[]{}|(2)(31)0A x x x a =--+< ，． （Ⅰ）当时，求;（Ⅱ）求使的实数 的取值范围． （16）（本小题满分13分）在等差数列｛}中，已知，， （Ⅰ）求数列｛}的通项； （Ⅱ）求数列｛}的前9项和; （Ⅲ）若，求数列的前项和.（17）（本小题满分13分）已知πθθ⎛⎫=∈ ⎪⎝⎭4cos ,0,52, （Ⅰ）求的值；（Ⅱ）求的值；（Ⅲ）求 的值．（18）（本小题满分13分）已知函数()sin 2cos 2f x x x ωω=+．（）的最小正周期为，（Ⅰ）求的值及函数的单调递减区间；（Ⅱ）将函数的图象上各点的横坐标向右平行移动个单位长度，纵坐标不变，得到函数的图象，求函数在上的最大值和最小值．（19）（本小题满分14分）已知函数，满足(0)2,(1)()21=+-=-f f x f x x（Ⅰ）求函数的解析式；（Ⅱ）当时，求函数的最大值和最小值.（Ⅲ）若函数的两个零点分别在区间和内，求的取值范围.（20）（本小题满分14分）已知：已知函数，（Ⅰ）若曲线在点处的切线的斜率为，求实数；（Ⅱ）若，求的极值；（Ⅲ）当时，在上的最小值为，求在该区间上的最大值．高三期中文科数学答案（xx 、11）一、选择题：本卷共8题，共40分。