面面平行的判定与性质

面面平行的断定与性质
假如一个平面内的两条相交直线和另一个平面内的两条相交直线分别平行，那么这两个平面平行。

假如一个平面内的两条相交直线和另一个平面内的两条相交直线分别平行，那么这两个平面平行。

面面平行的断定定理1、假如两个平面垂直于同一条直线，那么这两个平面平行。

2、假如一个平面内有两条相交直线与另一个平面平行，那么这两个平面平行。

3、假如一个平面内有两条相交直线分别与另一个平面内的两条相交直线平行，那么这两个平面平行。

面面平行的性质定理定理1
两个平面平行，在一个平面内的任意一条直线平行于另外一个平面。

证明：设α∥β，a?α，那么a∥β
∵α∥β
∴α与β无交点
又∵a?α
∴a与β无交点
即a∥β
定理2
两个平行平面，分别和第三个平面相交，交线平行。

假如交线不平行的话，设交线交点为P，那么P属于两条交线，即P属于两个平行平面，这是不可能的事情。

所以交线必定平行。

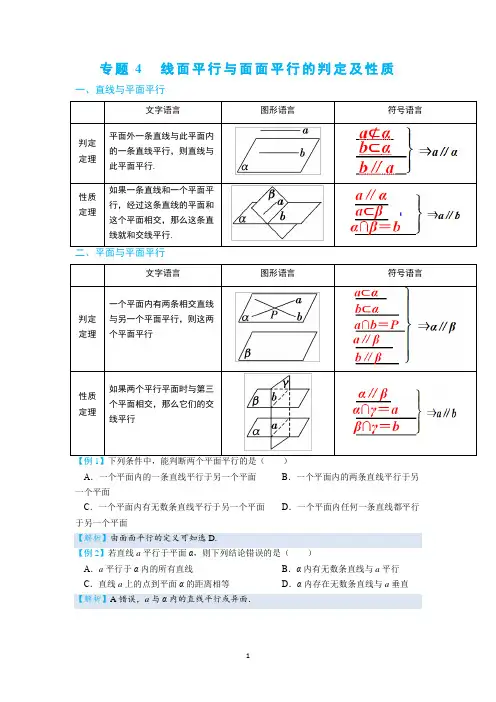
专题4 线面平行与面面平行的判定及性质一、直线与平面平行下列条件中，能判断两个平面平行的是（）A．一个平面内的一条直线平行于另一个平面B．一个平面内的两条直线平行于另一个平面C．一个平面内有无数条直线平行于另一个平面D．一个平面内任何一条直线都平行于另一个平面【解析】由面面平行的定义可知选D.【例2】若直线a平行于平面α，则下列结论错误的是（）A．a平行于α内的所有直线B．α内有无数条直线与a平行C．直线a上的点到平面α的距离相等D．α内存在无数条直线与a垂直【解析】A错误，a与α内的直线平行或异面．【例3】已知不重合的直线a ，b 和平面α，①若a ∥α，b ⊂α，则a ∥b ；②若a ∥α，b ∥α，则a ∥b ；③若a ∥b ，b ⊂α，则a ∥α；④若a ∥b ，a ∥α，则b ∥α或b ⊂α，上面命题中正确的是________(填序号)．【解析】 ①中a 与b 可能异面；②中a 与b 可能相交、平行或异面；③中a 可能在平面α内，④正确．【例4】已知α、β是平面，m 、n 是直线，给出下列命题：①若m ⊥α，m ⊂β，则α⊥β.②若m ⊂α，n ⊂α，m ∥β，n ∥β，则α∥β.③如果m ⊂α，α⊄n ，m 、n 是异面直线，那么n 与α相交．④若α∩β＝m ，n ∥m ，且α⊄n ，β⊄n ，则n ∥α且n ∥β其中正确命题的个数是（ ）A ．1B ．2C ．3D ．4【解析】对于①，由定理“如果一个平面经过另一个平面的一条垂线，那么这两个平面垂直”得知，①正确；对于②，注意到直线m ，n 可能是两条平行直线，此时平面α，β可能是相交平面，因此②不正确；对于③，满足条件的直线n 可能平行于平面α，因此③不正确；对于④，由定理“如果平面外一条直线平行于平面内一条直线，那么这条直线平行于这个平面”得知，④正确．综上所述，其中正确的命题是①④，故选B.【例5】已知m ，n 表示两条不同直线，α，β，γ表示不同平面，给出下列三个命题： ①n m n m //⇒⎩⎨⎧⊥⊥αα；①αα//n n m m ⇒⎩⎨⎧⊥⊥；①n m n m ⊥⇒⎩⎨⎧⊥αα//其中真命题的个数为（ ） A ．0 B ．1 C ．2 D ．3【解析】若⎩⎨⎧⊥⊥ααn m ，则m ①n ，即命题①正确；若⎩⎨⎧⊥⊥n m m α，则n ①α或n ①α，即命题①不正确；若⎩⎨⎧⊥αα//n m ，则m ①n ，即命题①正确；综上可得，真命题共有2个．故选C ．【例6】已知m 、n 、l 1、l 2表示直线，α、β表示平面．若m ⊂α，n ⊂α，l 1⊂β，l 2⊂β，l 1∩l 2＝M ，则以下条件中，能推出α∥β的是（ ） A ．m ∥β且l 1∥α B ．m ∥β且n ∥βC ．m ∥β且n ∥l 2D ．m ∥l 1且n ∥l 2【解析】由定理“如果一个平面内有两条相交直线分别与另一个平面平行，那么这两个平面平行”可得，由选项D 可推知α∥β.【例7】在下列条件中，可判断平面α与β平行的是（ ） A ．α、β都平行于直线l B ．α内存在不共线的三点到β的距离相等C ．l 、m 是α内两条直线，且l ①β，m ①βD ．l 、m 是两条异面直线，且l ①α，m ①α，l ①β，m ①β【解析】排除法，A 中α、β可以是相交平面；B 中三点可面平面两侧；C 中两直线可以不相交．故选D ，也可直接证明．【例8】经过平面外的两点作该平面的平行平面可以作（ ）A ．0个B ．1个C ．0个或1个D ．1个或2个【解析】这两点可以是在平面同侧或两侧．故选C ．达标训练11．（2019•延安一模）已知m ，n 表示两条不同的直线，α表示平面．下列说法正确的是（ ）A ．若//m α，//n α，则//m nB ．若m α⊥，n α⊥，则//m nC ．若m α⊥，m n ⊥，则//n αD ．若//m α，m n ⊥，则n α⊥ 2．（2019•湖北期中）平面α与平面β平行的条件可以是（ ）A ．α内有无数多条直线都与β平行B ．直线a α⊂，b β⊂，且//a β，//b αC ．直线//a α，//a β，且直线a 不在α内，也不在β内D ．一个平面α内两条不平行的直线都平行于另一个平面β3．（2019•深圳二模）己知正方体1111ABCD A B C D -，P 为棱1CC 的动点，Q 为棱1AA 的中点，设直线m 为平面BDP 与平面11B D P 的交线，以下关系中正确的是（ ） A ．1//m D Q B ．//m 平面11B D QC ．1m B Q ⊥D ．m ⊥平面11ABB A4．（2019•聊城二模）在长方体1111ABCD A B C D -中，F ，F ，G ，H 分别为棱11A B ，1BB ，1CC ，11C D 的中点，则下列结论中正确的是（ ）A ．1//AD 平面EFGHB ．1//BD GHC ．//BD EFD ．平面//EFGH 平面11A BCD5．（2019•汕头月考）如图，在正方体1111ABCD A B C D -中，M ，N 分别是1BC ，1CD 的中点，则下列判断错误的是（ ） A ．1MN CC ⊥B ．MN ⊥平面11ACC AC ．//MN 平面ABCDD ．11//MN A B6．（2019•大连一模）已知m ，n 为两条不重合直线，α，β为两个不重合平面，下列条件中，可以作为//αβ的充分条件的是（ ） A ．//m n ，m α⊂，n β⊂ B ．//m n ，m α⊥，n β⊥ C ．m n ⊥，//m α，//n βD ．m n ⊥，m α⊥，n β⊥7．（2019•汕头一模）在正方体1111ABCD A B C D -中，点O 是四边形ABCD 的中心，关于直线1A O ，下列说法正确的是（ ）A ．11//AO D C B ．1AO BC ⊥C ．1//A O 平面11B CDD ．1A O ⊥平面11AB D8．（2019•青云月考）如图，四棱锥P ABCD -中，M ，N 分别为AC ，PC 上的点，且//MN 平面PAD ，则（ ） A ．//MN PD B ．//MN PAC ．//MN ADD ．以上均有可能9．（2019•上饶一模）设m ，n 表示不同的直线，α，β表示不同的平面，且m ，n α⊂．则“//αβ”是“//m β且//n β”的（ ） A ．充分但不必要条件 B ．必要但不充分条件C ．充要条件D ．既不充分又不必要条件10．（2018•沧州一模）如图，在下列四个正方体中，P ，R ，Q ，M ，N ，G ，H 为所在棱的中点，则在这四个正方体中，阴影平面与PRQ 所在平面平行的是（ ）A ．B ．C ．D ．11．（2017•洛南期末）已知平面//α平面β，直线m α⊂，直线n β⊂，下列结论中不正确的是（ ） A ．//m βB ．//n αC ．//m nD ．m 与n 不相交12．（2018•杭州期中）如图，四棱锥P ABCD -的底面ABCD 是平行四边形，M 、N 分别为线段PC 、PB 上一点，若:3:1PM MC =，且//AN 平面BDM ，则:PN NB =（ ）A ．4:1B ．3:1C ．3:2D ．2:113．（2018•厦门二模）如图，在正方体1111ABCD A B C D -中，M ，N ，P 分别是11C D ，BC ，11A D 的中点，则下列命题正确的是（ ）A ．//MN APB ．1//MN BDC ．//MN 平面11BBD DD ．//MN 平面BDP14．（2018•辛集期中）在四棱锥P ABCD -中，底面ABCD 为菱形，60BAD ∠=︒，Q 为AD 的中点，点M 在线段PC 上，PM tPC =，//PA 平面MQB ，则实数t 的值为（ ） A ．15B ．14 C ．13D ．1215．（2018•四川模拟）如图是某几何体的平面展开图，其中四边形ABCD 为正方形，E ，F 分别为PA ，PD 的中点．在此几何体中，以下结论一定成立的是（ ） A ．直线//BE PFB ．直线//EF 平面PBCC ．平面BCE ⊥平面PAD D ．直线PB 与DC 所成角为60︒16．（2017•万州期末）平面α与ABC ∆的两边AB ，AC 分别交于点D ，E ，且::AD DB AE EC =，如图，则BC 与α的位置关系是（ ）A ．异面B ．相交C ．平行或相交D ．平行17．（2018•桃城模拟）如图，各棱长均为1的正三棱柱111ABC A B C -，M ，N 分别为线段1A B ，1B C 上的动点，且//MN 平面11ACC A ，则这样的MN 有（ ）A ．1条B ．2条C ．3条D ．无数条18．（2018•雁江月考）已知P 为ABC ∆所在平面外一点，平面//α平面ABC ，且α交线段PA ，PB ，PC 于点A '，B '，C '，若:2:3PA AA ''=，则:A B C ABC S S '''=△△（ ）A ．2:3B ．2:5C ．4:9D ．4:2519．（2018•香坊四模）对于不重合的两个平面α和β，给定下列条件： ①存在直线l ，使得l α⊥，且l β⊥； ①存在平面γ，使得αγ⊥且βγ⊥； ①α内有不共线的三点到β的距离相等；①存在异面直线l ，m ，使得//l α，//l β，//m α，//m β． 其中，可以判定α与β平行的条件有（ ） A ．1个B ．2个C ．3个D ．4个20．（2018•西城期末）在直三棱柱111ABC A B C -中，D 为1AA 中点，点P 在侧面11BCC B 上运动，当点P 满足条件 时，1//A P 平面BCD （答案不唯一，填一个满足题意的条件即可达标训练21．（2017•新课标①）如图，在下列四个正方体中，A ，B 为正方体的两个顶点，M ，N ，Q 为所在棱的中点，则在这四个正方体中，直线AB 与平面MNQ 不平行的是（ ）A ．B ．C ．D ．2．（2011•浙江）若直线l 不平行于平面α，且l α⊂/，则（ ） A ．α内存在直线与l 异面 B ．α内存在与l 平行的直线C ．α内存在唯一的直线与l 平行D ．α内的直线与l 都相交 3．（2010•浙江）设l ，m 是两条不同的直线，α是一个平面，则下列命题正确的是（ ） A ．若l m ⊥，m α⊂，则l α⊥ B ．若l α⊥，//l m ，则m α⊥C ．若//l α，m α⊂，则//l mD ．若//l α，//m α，则//l m 4．（2010•江西）如图，M 是正方体1111ABCD A B C D -的棱1DD 的中点，给出下列命题 ①过M 点有且只有一条直线与直线AB 、11B C 都相交； ①过M 点有且只有一条直线与直线AB 、11B C 都垂直； ①过M 点有且只有一个平面与直线AB 、11B C 都相交； ①过M 点有且只有一个平面与直线AB 、11B C 都平行． 其中真命题是（ ） A ．①①①B ．①①①C ．①①①D ．①①①5．（2008•湖南）已知直线m 、n 和平面α、β满足m n ⊥，m α⊥，αβ⊥，则（ ） A ．n β⊥ B ．//n β，或n β⊂ C ．n α⊥D ．//n α，或n α⊂6．（2007•北京）平面//α平面β的一个充分条件是（ ） A ．存在一条直线a ，//a α，//a β B ．存在一条直线a ，a α⊂，//a βC ．存在两条平行直线a ，b ，a α⊂，b β⊂，//a β，//b αD ．存在两条异面直线a ，b ，a α⊂，b β⊂，//a β，//b α7．（2011•福建）如图，正方体1111ABCD A B C D -中，2AB =，点E 为AD 的中点，点F 在CD 上，若//EF 平面1AB C ，则线段EF 的长度等于 ．。

温馨小提示：本文主要介绍的是关于面面平行定理和判定定理的文章，文章是由本店铺通过查阅资料，经过精心整理撰写而成。

文章的内容不一定符合大家的期望需求，还请各位根据自己的需求进行下载。

本文档下载后可以根据自己的实际情况进行任意改写，从而已达到各位的需求。

愿本篇面面平行定理和判定定理能真实确切的帮助各位。

本店铺将会继续努力、改进、创新，给大家提供更加优质符合大家需求的文档。

感谢支持！(Thank you fordownloading and checking it out!)面面平行定理和判定定理一、面面平行定理面面平行定理的定义：面面平行定理是立体几何中的一个重要定理，它描述了空间中两个平面之间的平行关系。

具体来说，面面平行定理是指，如果一个平面同时与两个平行平面相交，那么它与这两个平行平面的交线也是平行的。

面面平行定理的表述：面面平行定理可以表述为：在空间中，如果平面α与平面β平行，并且平面α与平面γ相交于一条直线l，那么平面β与平面γ也平行，且它们的交线m也与直线l平行。

面面平行定理的证明方法：面面平行定理的证明通常采用反证法。

首先假设平面β与平面γ不平行，那么它们必须相交于一条直线n。

根据平面与直线的位置关系，直线l与直线n 都在平面α内，因此直线l与直线n平行。

但是这与假设直线l与直线n不平行相矛盾。

因此，假设不成立，平面β与平面γ必须平行。

同理，可以证明平面β与平面γ的交线m也与直线l平行。

这样，面面平行定理得证。

二、判定定理面面平行定理和判定定理是空间几何中的重要理论，其中判定定理包括线线平行定理、线面平行定理和面面平行定理。

这些定理在空间几何图形的判定和空间几何问题的求解中具有广泛的应用。

判定定理的种类线线平行定理是指，如果两条直线在同一平面内，且它们的交线与第三条直线平行，则这两条直线平行。

线面平行定理是指，如果一条直线与一个平面平行，那么这条直线上的所有点都与这个平面平行。

面面平行定理是指，如果两个平面上的对应线段平行，则这两个平面平行。

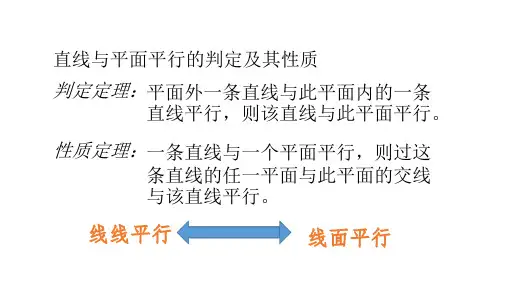
面面平行的判定公式在我们的数学世界里，面面平行可是一个相当有趣的概念，特别是它的判定公式，就像是一把神奇的钥匙，能帮我们打开几何世界的大门。

咱们先来说说什么是面面平行。

简单来讲，两个平面如果没有公共点，那就叫面面平行。

想象一下，家里的地板和天花板，它们就是平行的两个面，永远不会相交。

那怎么来判定两个平面是不是平行呢？这就轮到我们的判定公式登场啦！判定公式一：如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行。

比如说，在一个教室里，黑板所在的平面和对面墙所在的平面。

假设黑板平面内有两条相交的直线，一条是黑板的上边沿，另一条是黑板的左边沿，这两条直线都和对面墙平面内对应的两条直线平行，那黑板平面和对面墙平面就是平行的。

我记得有一次给学生们讲这个知识点的时候，有个调皮的小家伙就问我：“老师，那要是这两条直线不相交呢？”我笑着回答他：“那可不行哦，如果这两条直线不相交，就没法确定一个平面啦，就像你在操场上随便画两条不相交的直线，它们可不能确定一个固定的区域，是不是？”小家伙恍然大悟地点点头。

判定公式二：如果两个平面都垂直于同一条直线，那么这两个平面平行。

这就好比两根笔直的电线杆，它们都垂直于地面，那它们所在的平面也就和地面平行啦。

还有啊，在实际解题中，可不能死记硬背这些公式，得灵活运用。

有时候题目会故意给你设置一些小陷阱，就看你能不能识破啦。

比如说，有一道题是这样的：一个平面内有三条直线，其中两条平行，另一条与这两条相交，问这两个平面是否平行。

这时候就得仔细分析了，别一看有平行的直线就匆忙下结论。

学习面面平行的判定公式，就像是在搭建一座知识的大厦，每一块砖头都要放对位置，才能让这座大厦稳稳当当。

希望同学们在面对这些知识的时候，都能像勇敢的探险家，不怕困难，勇往直前，把面面平行的判定公式掌握得牢牢的！这样在数学的海洋里，就能更加自由自在地遨游啦！。

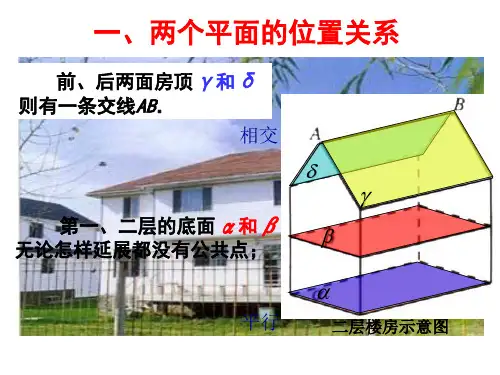
线面、面面平行的判定与性质（教师版）知识回顾1．线面平行的判定（1）直线与平面平行的定义：直线与平面无公共点． （2）直线与平面平行的判定定理：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行． 用符号表示为：a ⊄α，b ⊂α，且a ∥b ⇒a ∥α． 2．线面平行的性质直线与平面平行的性质定理：一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行符号语言描述：⎭⎪⎬⎪⎫a ∥αa ⊂ββ∩α＝b ⇒a ∥b ． 3. 面面平行的判定（1）平面α与平面β平行的定义：两平面无公共点． （2）直线与平面平行的判定定理：下面的命题在“________”处缺少一个条件，补上这个条件，使其构成真命题(m ，n 为直线，α，β为平面)，则此条件应为m ，n 相交．⎭⎪⎬⎪⎫m ⊂αn ⊂αm ∥βn ∥β⇒α∥β 4．面面平行的性质平面与平面平行的性质定理：如果两个平行平面同时和第三个平面相交，那么它们的交线平行．符号表示为：⎭⎪⎬⎪⎫α∥βα∩γ＝a β∩γ＝b ⇒a ∥b ． 题型讲解题型一 利用三角形中位线证明线面平行例1、如图，ABCD 是平行四边形，S 是平面ABCD 外一点，M 为SC 的中点.求证：SA∥平面MDB.答案:证明：连结AC交BD于N，因为ABCD是平行四边形，所以N是AC的中点.又因为M是SC的中点，所以MN∥SA.因为MN平面MDB，所以SA∥平面MDB.例2、如图,已知点M、N是正方体ABCD-A1B1C1D1的两棱A1A与A1B1的中点，P是正方形ABCD的中心，求证：MN∥平面PB1C.答案证明：如图，连结AC，则P为AC的中点，连结AB1，∵M、N分别是A1A与A1B1的中点，∴MN∥AB1.又∵平面PB1C，平面PB1C，故MN∥面PB1C.例3、如图所示，P是▱ABCD所在平面外一点，E、F分别在PA、BD上，且PE∶EA＝BF∶FD．求证：EF∥平面PBC．证明连接AF延长交BC于G，连接PG．在▱ABCD中，易证△BFG∽△DFA．∴GFFA＝BFFD＝PEEA，∴EF∥PG．而EF⊄平面PBC，PG⊂平面PBC，∴EF∥平面PBC．练习在正方体ABCD－A1B1C1D1中，E为DD1的中点，则BD1与过点A，E，C的平面的位置关系是______．答案：平行题型二利用平行四边形证明线面平行例1、如图所示，在正方体ABCD—A1B1C1D1中，E、F分别是棱BC、C1D1的中点．求证：EF∥平面BDD1B1．证明：取D1B1的中点O，连接OF，OB．∵OF 12B1C1，BE12B1C1，∴OF BE．∴四边形OFEB是平行四边形，∴EF∥BO．∵EF⊄平面BDD1B1，BO⊂平面BDD1B1，∴EF∥平面BDD1B1．例2、如图所示，已知正方体ABCD－A1B1C1D1中，面对角线AB1、BC1上分别有两点E、F，且B1E＝C1F．求证：EF∥平面ABCD．证明方法一过E、F分别作AB、BC的垂线，EM、FN分别交AB、BC于M、N，连接MN．∵BB1⊥平面ABCD，∴BB1⊥AB，BB1⊥BC，∴EM∥BB1，FN∥BB1，∴EM∥FN，∵AB1＝BC1，B1E＝C1F，∴AE＝BF，又∠B1AB＝∠C1BC＝45°，∴Rt△AME≌Rt△BNF，∴EM＝FN．∴四边形MNFE是平行四边形，∴EF∥MN．又MN⊂平面ABCD，EF⊄平面ABCD，∴EF∥平面ABCD．方法二过E作EG∥AB交BB1于G，连接GF，∴B1EB1A＝B1GB1B，B1E＝C1F，B1A＝C1B，∴C1FC1B＝B1GB1B，∴FG∥B1C1∥BC．又∵EG∩FG＝G，AB∩BC＝B，∴平面EFG∥平面ABCD．又EF⊂平面EFG，∴EF∥平面ABCD．题型三利用面面平行证明线面平行例. 如图，在四棱锥中，是平行四边形，，分别是，的中点．求证：平面．答案：证明：如图，取的中点，连接，，分别是，的中点，，，P ABCDABCD M N AB PCMN//PADCD E NE ME∵M N AB PCNE PD∴//ME AD//可证明平面，平面．又，平面平面，又平面，平面．题型四面面平行的证明例1、如图所示，在正方体ABCD—A1B1C1D1中，O为底面ABCD的中心，P是DD1的中点，设Q是CC1上的点，问：当点Q在什么位置时，平面D1BQ∥平面PAO?解：当Q为CC1的中点时，平面D1BQ∥平面PAO．∵Q为CC1的中点，P为DD1的中点，∴QB∥PA．∵P、O为DD1、DB的中点，∴D1B∥PO．又PO∩PA＝P，D1B∩QB＝B，D1B∥平面PAO，QB∥平面PAO，∴平面D1BQ∥平面PAO．题型五平行性质NE//PAD ME//PADNE ME E=∴MNE//PADMN⊂MNE∴MN//PAD例1、如图所示，长方体ABCD－A1B1C1D1中，E、F分别是棱AA1和BB1的中点，过EF的平面EFGH分别交BC和AD于G、H，则HG与AB的位置关系是()A．平行 B．相交C．异面 D．平行和异面答案：A例2、ABCD是平行四边形，点P是平面ABCD外一点，M是PC的中点，在DM上取一点G，过G和AP作平面交平面BDM于GH，求证：AP∥GH．证明如图所示，连接AC交BD于O，连接MO，∵ABCD是平行四边形，∴O是AC中点，又M是PC的中点，∴AP∥OM．根据直线和平面平行的判定定理，则有PA∥平面BMD．∵平面PAHG∩平面BMD＝GH，根据直线和平面平行的性质定理，∴AP∥GH．练习、如图，在三棱柱ABC－A1B1C1中，M是A1C1的中点，平面AB1M∥平面BC1N，AC∩平面BC1N＝N．求证：N为AC的中点．证明 ∵平面AB 1M ∥平面BC 1N ， 平面ACC 1A 1∩平面AB 1M ＝AM ， 平面BC 1N∩平面ACC 1A 1＝C 1N ， ∴C 1N ∥AM ，又AC ∥A 1C 1， ∴四边形ANC 1M 为平行四边形， ∴AN 綊C 1M ＝12A 1C 1＝12AC ，∴N 为AC 的中点．跟踪训练1．如右图所示的三棱柱ABC －A 1B 1C 1中，过A 1B 1的平面与平面ABC 交于直线DE ，则DE 与AB 的位置关系是( )A ．异面B ．平行C ．相交D ．以上均有可能 答案：B[解析] ∵A 1B 1∥AB ，AB ⊂平面ABC ，A 1B 1⊄平面ABC ， ∴A 1B 1∥平面ABC.又A 1B 1⊂平面A 1B 1ED ，平面A 1B 1ED∩平面ABC ＝DE ，∴DE ∥A 1B 1. 又AB ∥A 1B 1，∴DE ∥AB.2．已知直线l ，m ，平面α，β，下列命题正确的是( ) A ．l ∥β，l ⊂α⇒α∥βB ．l ∥β，m ∥β，l ⊂α，m ⊂α⇒α∥βC ．l ∥m ，l ⊂α，m ⊂β⇒α∥βD ．l ∥β，m ∥β，l ⊂α，m ⊂α，l ∩m ＝M ⇒α∥β 答案：D3、直线a ∥平面α，α内有n 条直线交于一点，则这n 条直线中与直线a 平行的直线( )A．至少有一条 B．至多有一条C．有且只有一条 D．没有答案：B4、给出下列结论，正确的有()①平行于同一条直线的两个平面平行；②平行于同一平面的两个平面平行；③过平面外两点，不能作一个平面与已知平面平行；④若a，b为异面直线，则过a与b平行的平面只有一个．A．1个 B．2个 C．3个 D．4个答案：B5．正方体EFGH—E1F1G1H1中，下列四对截面中，彼此平行的一对截面是()A．平面E1FG1与平面EGH1B．平面FHG1与平面F1H1GC．平面F1H1H与平面FHE1D．平面E1HG1与平面EH1G答案：A6．如图是长方体被一平面所截得的几何体，四边形EFGH为截面，则四边形EFGH的形状为________．答案：平行四边形[解析]∵平面ABFE∥平面CDHG，又平面EFGH∩平面ABFE＝EF，平面EFGH∩平面CDHG＝HG，∴EF∥HG.同理EH∥FG，∴四边形EFGH的形状是平行四边形．7. 如图所示，在三棱柱ABC－A1B1C1中，AC＝BC，点D是AB的中点，求证：BC1∥平面CA1D.证明：如图所示，连接AC1交A1C于点O，连接OD，则O是AC1的中点．∵点D是AB的中点，∴OD∥BC1.又∵OD⊂平面CA1D，BC1⊄平面CA1D，∴BC1∥平面CA1D.8．如图所示，在正方体ABCD－A1B1C1D1中，S是B1D1的中点，E、F、G分别是BC、DC和SC的中点．求证：平面EFG∥平面BDD 1B1．证明如图所示，连接SB，SD，∵F、G分别是DC、SC的中点，∴FG∥SD．又∵SD⊂平面BDD1B1，FG⊄平面BDD1B1，∴直线FG∥平面BDD1B1．同理可证EG∥平面BDD1B1，又∵EG⊂平面EFG，FG⊂平面EFG，EG∩FG＝G，∴平面EFG∥平面BDD1B1．9．（本小题满分12分）在四棱锥S－ABCD中，底面ABCD是正方形， M、N分别为AB、SC的中点，SA⊥底面ABCD．求证：//MN平面SAD；答案．证明（Ⅰ）： E 为SD 中点，连接AE ，NE ，因为M 、N 分别为AB 、SC 的中点，所以AM//EN ，AM=EN ，即四边形AMNE 是平行四边形，所以MN//AE ，可得//MN 平面SAD ；10. 一个多面体的直观图及三视图如图所示：(其中M 、N 分别是AF 、BC 的中点)．(1)求证：MN ∥平面CDEF ；(2)求多面体A －CDEF 的体积．答案 由三视图可知，该多面体是底面为直角三角形的直三棱柱ADE-BCF ，且AB =BC =BF=2，DE =CF=2，∴∠CBF =. (1)证明：取BF 的中点G ，连结MG 、NG ，由M 、N 分别为AF 、BC 的中点可得，NG ∥CF ，MG ∥EF ，∴平面MNG ∥平面CDEF ，又MN ⊂平面MNG ，∴MN ∥平面CDEF .(2)取DE 的中点H .∵AD =AE ，∴AH ⊥DE ， 在直三棱柱ADE-BCF 中，平面ADE ⊥平面CDEF ，平面A DE ∩平面CDEF=DE .∴AH ⊥平面CDEF.∴多面体A-CDEF 是以AH 为高，以矩形CDE F 为底面的棱锥，在△ADE 中，AH =. S 矩形CDEF =DE ·EF =4，∴棱锥A-CDEF 的体积为2222V=·S 矩形CDEF ·AH =×4×= 解法2：13218222323A CDEF AED BFC A BFCAED V V V S AB S AB ---=-=⨯-⨯⨯=⨯⨯⨯⨯=△△BFC 11如图，在直四棱柱ABCD －A 1B 1C 1D 1中，底面ABCD 为等腰梯形，AB ∥CD ，且AB ＝2CD ，在棱AB 上是否存在一点F ，使平面C 1CF ∥平面ADD 1A 1？若存在，求点F 的位置；若不存在，请说明理由．答案 存在这样的点F ，使平面C 1CF ∥平面ADD 1A 1，此时点F 为AB的中点，证明如下：∵AB ∥CD ，AB ＝2CD ，∴AF ∥CD ，∴四边形AFCD 是平行四边形，∴AD ∥CF ，又AD ⊂平面ADD 1A 1，CF ⊄平面ADD 1A 1，∴CF ∥平面ADD 1A 1.又CC 1∥DD 1，CC 1⊄平面ADD 1A 1，DD 1⊂平面ADD 1A 1，∴CC 1∥平面ADD 1A 1，又CC 1、CF ⊂平面C 1CF ，CC 1∩CF ＝C ，∴平面C 1CF ∥平面ADD 1A 1.12. 如图，在底面是平行四边形的四棱锥P －ABCD 中，点E 在PD 上，且PE ∶ED ＝2∶1，在棱PC 上是否存在一点F ，使BF ∥平面AEC ？证明你的结论．答案 存在．证明如下：取棱PC 的中点F ，线段PE 的中点M ，连接BD .设BD ∩AC ＝O .连接BF ，MF ，BM ，OE .13132283∵PE ∶ED ＝2∶1，F 为PC 的中点，M 是PE 的中点，E 是MD的中点，∴MF ∥EC ，BM ∥OE .∵MF ⊄平面AEC ，CE ⊂平面AEC ，BM ⊄平面AEC ，OE ⊂平面AEC ，∴MF ∥平面AEC ，BM ∥平面AEC .∵MF ∩BM ＝M ，∴平面BMF ∥平面AEC .又BF ⊂平面BMF ，∴BF ∥平面AEC .13. (北京)如图，在四面体PABC 中，PC ⊥AB ，PA ⊥BC ，点D ，E ，F ，G 分别是棱AP ，AC ，BC ，PB 的中点．(1)求证：DE ∥平面BCP ；(2)求证：四边形DEFG 为矩形；(3)是否存在点Q ，到四面体PABC 六条棱的中点的距离相等？说明理由．答案 (1)证明：因为D ，E 分别为AP ，AC 的中点，所以DE ∥PC .又因为DE ⊄平面BCP ，PC ⊂平面BCP ，所以DE ∥平面BCP .(2)证明：因为D ，E ，F ，G 分别为AP ，AC ，BC ，PB 的中点所以DE ∥PC ∥FG ，DG ∥AB ∥EF ，所以四边形DEFG 为平行四边形．又因为PC ⊥AB ，所以DE ⊥DG ，所以四边形DEFG 为矩形．(3)存在点Q 满足条件，理由如下：连接DF ，EG ，设Q 为EG 的中点．由(2)知，DF ∩EG ＝Q ，且QD ＝QE ＝QF ＝QG ＝12EG .分别取PC ，AB 的中点M ，N ，连接ME ，EN ，NG ，MG ，MN .与(2)同理可证四边形MENG 为矩形，其对象线交点为EG 的中点Q ，且QM ＝QN ＝12EG ，所以EG 的中点Q 是满足条件的点．。

面面平行怎么证明面面平行怎么证明三篇面面平行要证明证明可不容易，因为牵扯的公式是很多的。

下面就是店铺给大家整理的面面平行的证明内容，希望大家喜欢。

面面平行的证明方法一判定定理：如果一个平面内的两条相交直线都平行于另一个平面，那么这两个平面平行。

反证：记其中一个平面内的两条相交直线为a，b。

假设这两个平面不平行，设交线为l，则a∥l(过平面外一条与平面平行的.直线的平面与该平面的交线平行于该直线)，b∥l，则a∥b，与a，b相交矛盾，故假设不成立，所以这两个平面平行。

证明：∵平面α∥平面β∴平面α和平面β没有公共点又a 在平面α上，b 在平面β上∴直线a、b没有公共点又∵α∩γ=a，β∩γ=b∴a在平面γ上，b 在平面γ上∴a∥b.面面平行的证明方法二用反证法命题：已知α∥β，AB∈α,求证：AB∥β证明:假设AB不平行于β则AB交β于点P，点P∈β又因为P∈AB，所以P∈αα、β有公共点P，与命题α∥β不符，所以AB∥β。

【直线与平面平行的判定】定理：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行。

【判断直线与平面平行的方法】(1)利用定义：证明直线与平面无公共点;(2)利用判定定理：从直线与直线平行得到直线与平面平行;(3)利用面面平行的性质：两个平面平行，则一个平面内的直线必平行于另一个面面平行的证明方法三证明：∵平面α∥平面β∴平面α和平面β没有公共点又a 在平面α上，b 在平面β上∴直线a、b没有公共点又∵α∩γ=a，β∩γ=b∴a在平面γ上，b 在平面γ上∴a∥b.证明：∵平面α∥平面β∴平面α和平面β没有公共点又a 在平面α上，b 在平面β上∴直线a、b没有公共点又∵α∩γ=a，β∩γ=b∴a在平面γ上，b 在平面γ上∴a∥b.下载全文。