面面平行的判定及性质定理

温馨小提示：本文主要介绍的是关于面面平行定理和判定定理的文章，文章是由本店铺通过查阅资料，经过精心整理撰写而成。

文章的内容不一定符合大家的期望需求，还请各位根据自己的需求进行下载。

本文档下载后可以根据自己的实际情况进行任意改写，从而已达到各位的需求。

愿本篇面面平行定理和判定定理能真实确切的帮助各位。

本店铺将会继续努力、改进、创新，给大家提供更加优质符合大家需求的文档。

感谢支持！(Thank you fordownloading and checking it out!)面面平行定理和判定定理一、面面平行定理面面平行定理的定义：面面平行定理是立体几何中的一个重要定理，它描述了空间中两个平面之间的平行关系。

具体来说，面面平行定理是指，如果一个平面同时与两个平行平面相交，那么它与这两个平行平面的交线也是平行的。

面面平行定理的表述：面面平行定理可以表述为：在空间中，如果平面α与平面β平行，并且平面α与平面γ相交于一条直线l，那么平面β与平面γ也平行，且它们的交线m也与直线l平行。

面面平行定理的证明方法：面面平行定理的证明通常采用反证法。

首先假设平面β与平面γ不平行，那么它们必须相交于一条直线n。

根据平面与直线的位置关系，直线l与直线n 都在平面α内，因此直线l与直线n平行。

但是这与假设直线l与直线n不平行相矛盾。

因此，假设不成立，平面β与平面γ必须平行。

同理，可以证明平面β与平面γ的交线m也与直线l平行。

这样，面面平行定理得证。

二、判定定理面面平行定理和判定定理是空间几何中的重要理论，其中判定定理包括线线平行定理、线面平行定理和面面平行定理。

这些定理在空间几何图形的判定和空间几何问题的求解中具有广泛的应用。

判定定理的种类线线平行定理是指，如果两条直线在同一平面内，且它们的交线与第三条直线平行，则这两条直线平行。

线面平行定理是指，如果一条直线与一个平面平行，那么这条直线上的所有点都与这个平面平行。

面面平行定理是指，如果两个平面上的对应线段平行，则这两个平面平行。

证明面面平行的判定定理
面面平行是立体几何学中一个非常重要的概念。

在三维空间中，
如果两个平面是平行的，那么它们永远不会相交。

而面面平行的判定
定理可以帮助我们准确地判断两个平面是否平行。

本文将详细介绍面
面平行的判定定理，包括定义、性质和应用。

一、定义
在三维空间中，两个平面是平行的，当且仅当它们的法线向量平行。

因此，要判断两个平面是否平行，我们只需要比较它们的法线向
量是否平行即可。

二、性质
1. 如果两个平面是平行的，那么它们永远不会相交。

2. 两个平面的法线向量分别为n和m，如果n和m平行，那么这
两个平面是平行的。

3. 如果两个平面是平行的，那么它们的法线向量长度相等。

三、应用
在求解立体几何学问题时，面面平行的判定定理是非常有用的。

比如，在计算两个平面之间的距离时，我们可以先判断它们是否平行，再利用向量的知识求解距离。

又比如，在求解两个平面的夹角时，我
们也可以利用这个定理来进行计算。

另外，在工程和建筑设计中，面面平行的判定定理也有着广泛的应用。

比如，在设计房屋或者建筑物时，我们需要保证墙壁之间是平行的，才能保证建筑物的稳定性和美观性。

此外，在工程测量中，面面平行的判定定理也可以用来判断不同建筑物的墙面是否平行，从而帮助我们得出准确的测量结果。

综上所述，面面平行的判定定理是立体几何学中一个非常重要的定理，它可以帮助我们准确地判断两个平面是否平行，并在工程、建筑设计和测量方面有着广泛的应用。

因此，学好面面平行的判定定理对我们的学习和工作都是非常有帮助的。

两平面平行的性质
两个平面平行，在一个平面内的任意一条直线平行于另外一个平面；2.两个平面平行，和一个平面垂直的直线必垂直于另外一个平面；3.两个平行平面，分别和第三个平面相交，交线平行。

线面平行的判定
定理1：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行。

已知：a∥b，α不包含a，α包含b，求证：a∥α
向量法证明：设a的方向向量为a，b的方向向量为b，面α的法向量为p。

∵α包含b
∴b⊥p，即p·b=0∵a∥b，由共线向量基本定理可知存在一实数k使得a=kb
那么p·a=p·kb=kp·b=0 即a⊥p ∴a∥α
定理2：平面外一条直线与此平面的垂线垂直，则这条直线与此平面平行。

已知：a⊥b，b⊥α，且a不在α上。

求证：a∥α
证明：设a与b的垂足为A，b与α的垂足为B。

假设a与α不平行，那么它们相交，设a∩α=C，连接BC由于不在直线上的三个点确定一个平面，因此ABC首尾相连得到△ABC
∵B∈α，C∈α，b⊥α∴b⊥BC，即∠ABC=90°
∵a⊥b，即∠BAC=90°∴在△ABC中，有两个内角为90°，这是不可能的事情。

∴假设不成立，a∥α。

1线面平行的判定定理：
如果平面外一条直线与此平面内的一条直线平行，那么该直线与此平面平行.
2线面平行的性质定理：
一条直线与一个平面平行，如果过该直线的平面与此平面相交，那么该直线与交线平行.
3面面平行的判定定理：
如果一个平面内的两条相交直线与另一个平面平行，那么这两个平面平行.
4面面平行的性质定理：
两个平面平行，如果另一个平面与这两个平面相交，那么两条交线平行
. 5线面垂直的判定定理：
如果一条直线与一个平面内的两条相交直线垂直，那么该直线与此平面垂直.
6线面垂直的性质定理：
垂直于同一个平面的两条直线平行.
7面面垂直的判定定理：
如果一个平面过另一个平面的垂线，那么这两个平面垂直.
8面面垂直的性质定理：
两个平面垂直，如果一个平面内有一直线垂直于这两个平面的交线，那么这条直线与另一个平面垂直.。

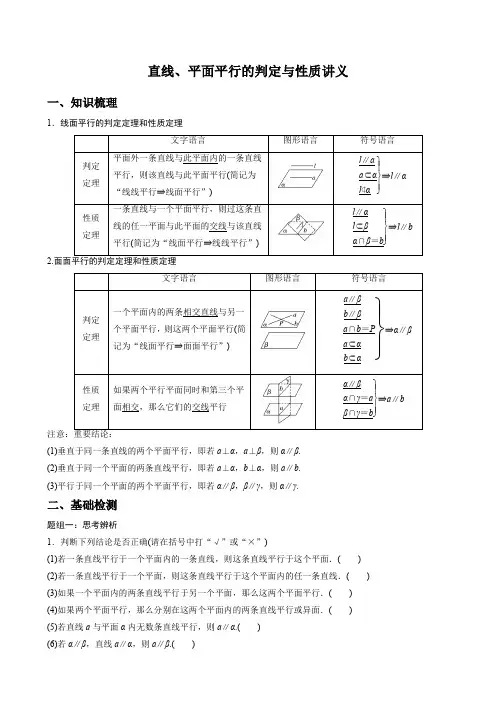
直线、平面平行的判定与性质讲义一、知识梳理1．线面平行的判定定理和性质定理文字语言图形语言符号语言判定定理平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行(简记为“线线平行⇒线面平行”)⎭⎪⎬⎪⎫l∥aa⊂αl⊄α⇒l∥α性质定理一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行(简记为“线面平行⇒线线平行”)⎭⎪⎬⎪⎫l∥αl⊂βα∩β＝b⇒l∥b2.面面平行的判定定理和性质定理文字语言图形语言符号语言判定定理一个平面内的两条相交直线与另一个平面平行，则这两个平面平行(简记为“线面平行⇒面面平行”)⎭⎪⎬⎪⎫a∥βb∥βa∩b＝Pa⊂αb⊂α⇒α∥β性质定理如果两个平行平面同时和第三个平面相交，那么它们的交线平行⎭⎪⎬⎪⎫α∥βα∩γ＝aβ∩γ＝b⇒a∥b(1)垂直于同一条直线的两个平面平行，即若a⊥α，a⊥β，则α∥β.(2)垂直于同一个平面的两条直线平行，即若a⊥α，b⊥α，则a∥b.(3)平行于同一个平面的两个平面平行，即若α∥β，β∥γ，则α∥γ.二、基础检测题组一：思考辨析1．判断下列结论是否正确(请在括号中打“√”或“×”)(1)若一条直线平行于一个平面内的一条直线，则这条直线平行于这个平面．()(2)若一条直线平行于一个平面，则这条直线平行于这个平面内的任一条直线．()(3)如果一个平面内的两条直线平行于另一个平面，那么这两个平面平行．()(4)如果两个平面平行，那么分别在这两个平面内的两条直线平行或异面．()(5)若直线a与平面α内无数条直线平行，则a∥α.()(6)若α∥β，直线a∥α，则a∥β.()题组二：教材改编2．下列命题中正确的是( )A ．若a ，b 是两条直线，且a ∥b ，那么a 平行于经过b 的任何平面B ．若直线a 和平面α满足a ∥α，那么a 与α内的任何直线平行C ．平行于同一条直线的两个平面平行D ．若直线a ，b 和平面α满足a ∥b ，a ∥α，b ⊄α，则b ∥α3．如图，在正方体ABCD －A 1B 1C 1D 1中，E 为DD 1的中点，则BD 1与平面AEC 的位置关系为________．题组三：易错自纠4．若平面α∥平面β，直线a ∥平面α，点B ∈β，则在平面β内且过B 点的所有直线中( ) A ．不一定存在与a 平行的直线 B ．只有两条与a 平行的直线 C ．存在无数条与a 平行的直线 D ．存在唯一与a 平行的直线 5．设α，β，γ为三个不同的平面，a ，b 为直线，给出下列条件： ①a ⊂α，b ⊂β，a ∥β，b ∥α；②α∥γ，β∥γ； ③α⊥γ，β⊥γ；④a ⊥α，b ⊥β，a ∥b .其中能推出α∥β的条件是______．(填上所有正确的序号)6.如图是长方体被一平面所截得的几何体，四边形EFGH 为截面，则四边形EFGH 的形状为________．三、典型例题题型一：直线与平面平行的判定与性质 命题点1：直线与平面平行的判定典例 如图，在四棱锥P －ABCD 中，AD ∥BC ，AB ＝BC ＝12AD ，E ，F ，H 分别为线段AD ，PC ，CD 的中点，AC 与BE 交于O 点，G 是线段OF 上一点．(1)求证：AP∥平面BEF；(2)求证：GH∥平面P AD.命题点2：直线与平面平行的性质典例如图，四棱锥P－ABCD的底面是边长为8的正方形，四条侧棱长均为217.点G，E，F，H分别是棱PB，AB，CD，PC上共面的四点，平面GEFH⊥平面ABCD，BC∥平面GEFH.(1)证明：GH∥EF；(2)若EB＝2，求四边形GEFH的面积．思维升华：判断或证明线面平行的常用方法(1)利用线面平行的定义(无公共点)．(2)利用线面平行的判定定理(a⊄α，b⊂α，a∥b⇒a∥α)．(3)利用面面平行的性质(α∥β，a⊂α⇒a∥β)．(4)利用面面平行的性质(α∥β，a⊄α，a⊄β，a∥α⇒a∥β)．跟踪训练如图，四棱锥P-ABCD中，P A⊥底面ABCD，AD∥BC，AB＝AD＝AC＝3，P A＝BC＝4，M为线段AD上一点，AM＝2MD，N为PC的中点．(1)证明：MN∥平面P AB；(2)求四面体N-BCM的体积．题型二：平面与平面平行的判定与性质典例如图所示，在三棱柱ABC－A1B1C1中，E，F，G，H分别是AB，AC，A1B1，A1C1的中点，求证：(1)B，C，H，G四点共面；(2)平面EF A1∥平面BCHG.引申探究：本例条件下，若D1，D分别为B1C1，BC的中点，求证：平面A1BD1∥平面AC1D.思维升华：证明面面平行的方法(1)面面平行的定义．(2)面面平行的判定定理：如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行．(3)利用垂直于同一条直线的两个平面平行．(4)两个平面同时平行于第三个平面，那么这两个平面平行．(5)利用“线线平行”“线面平行”“面面平行”的相互转化．跟踪训练：如图所示，四边形ABCD与四边形ADEF都为平行四边形，M，N，G分别是AB，AD，EF的中点．求证：(1)BE∥平面DMF；(2)平面BDE∥平面MNG.题型三：平行关系的综合应用典例如图所示，平面α∥平面β，点A∈α，点C∈α，点B∈β，点D∈β，点E，F分别在线段AB，CD 上，且AE∶EB＝CF∶FD.(1)求证：EF∥平面β；(2)若E，F分别是AB，CD的中点，AC＝4，BD＝6，且AC，BD所成的角为60°，求EF的长．思维升华：利用线面平行的性质，可以实现与线线平行的转化，尤其在截面图的画法中，常用来确定交线的位置，对于最值问题，常用函数思想来解决．跟踪训练如图所示，四边形EFGH为空间四边形ABCD的一个截面，若截面为平行四边形．(1)求证：AB∥平面EFGH，CD∥平面EFGH；(2)若AB＝4，CD＝6，求四边形EFGH周长的取值范围．四、反馈练习1．若直线l不平行于平面α，且l⊄α，则()A．α内的所有直线与l异面B．α内不存在与l平行的直线C．α与直线l至少有两个公共点D．α内的直线与l都相交2．已知直线a和平面α，那么a∥α的一个充分条件是()A．存在一条直线b，a∥b且b⊂αB．存在一条直线b，a⊥b且b⊥αC．存在一个平面β，a⊂β且α∥βD．存在一个平面β，a∥β且α∥β3．平面α∥平面β，点A，C∈α，点B，D∈β，则直线AC∥直线BD的充要条件是()A．AB∥CD B．AD∥CBC．AB与CD相交D．A，B，C，D四点共面4．一条直线l上有相异的三个点A，B，C到平面α的距离相等，那么直线l与平面α的位置关系是() A．l∥αB．l⊥αC．l与α相交但不垂直D．l∥α或l⊂α5．对于空间中的两条直线m，n和一个平面α，下列命题中的真命题是()A．若m∥α，n∥α，则m∥nB．若m∥α，n⊂α，则m∥nC．若m∥α，n⊥α，则m∥nD．若m⊥α，n⊥α，则m∥n6．如图，L，M，N分别为正方体对应棱的中点，则平面LMN与平面PQR的位置关系是()A．垂直B．相交不垂直C．平行D．重合7．在四面体A－BCD中，M，N分别是△ACD，△BCD的重心，则四面体的四个面中与MN平行的是________．8．设α，β，γ是三个不同的平面，m，n是两条不同的直线，在命题“α∩β＝m，n⊂γ，且________，则m∥n”中的横线处填入下列三组条件中的一组，使该命题为真命题．①α∥γ，n⊂β；②m∥γ，n∥β；③n∥β，m⊂γ.可以填入的条件有________．9．如图所示，在正四棱柱ABCD—A1B1C1D1中，E，F，G，H分别是棱CC1，C1D1，D1D，DC的中点，N是BC的中点，点M在四边形EFGH及其内部运动，则M只需满足条件______时，就有MN∥平面B1BDD1.(注：请填上你认为正确的一个条件即可，不必考虑全部可能情况)10．将一个真命题中的“平面”换成“直线”、“直线”换成“平面”后仍是真命题，则该命题称为“可换命题”．给出下列四个命题：①垂直于同一平面的两直线平行；②垂直于同一平面的两平面平行；③平行于同一直线的两直线平行；④平行于同一平面的两直线平行．其中是“可换命题”的是______．(填序号)11．如图，在四棱锥P—ABCD中，平面P AD⊥平面ABCD，底面ABCD为梯形，AB∥CD，AB＝2DC＝23，且△P AD与△ABD均为正三角形，E为AD的中点，G为△P AD的重心．(1)求证：GF∥平面PDC；(2)求三棱锥G—PCD的体积．12.如图，在四棱锥P－ABCD中，PD⊥平面ABCD，底面ABCD为正方形，BC＝PD＝2，E为PC的中点，CB＝3CG.(1)求证：PC⊥BC；(2)AD边上是否存在一点M，使得P A∥平面MEG？若存在，求出AM的长；若不存在，请说明理由．13．在四面体ABCD中，截面PQMN是正方形，则在下列结论中，错误的是()A．AC⊥BDB．AC∥截面PQMNC．AC＝BDD．异面直线PM与BD所成的角为45°14．过三棱柱ABC—A1B1C1的任意两条棱的中点作直线，其中与平面ABB1A1平行的直线共有________条．15．如图所示，侧棱与底面垂直，且底面为正方形的四棱柱ABCD—A1B1C1D1中，AA1＝2，AB＝1，M，N 分别在AD1，BC上移动，始终保持MN∥平面DCC1D1，设BN＝x，MN＝y，则函数y＝f(x)的图象大致是()16．在三棱锥S－ABC中，△ABC是边长为6的正三角形，SA＝SB＝SC＝15，平面DEFH分别与AB，BC，SC，SA交于点D，E，F，H.D，E分别是AB，BC的中点，如果直线SB∥平面DEFH，那么四边形DEFH 的面积为________．。

面面平行的性质定理
面面平行的性质定理：两个平面平行，在一个平面内的任意一条直线平行于另外一个平面。

两个平行平面，分别和第三个平面相交，交线平行。

两个平面平行，和一个平面垂直的直线必垂直于另外一个平面。

面面平行的性质定理：两个平面平行，在一个平面内的任意一条直线平行于另外一个平面。

两个平行平面，分别和第三个平面相交，交线平行。

两个平面平行，和一个平面垂直的直线必垂直于另外一个平面。

6条性质定理
定理1
两个平面平行，在一个平面内的任意一条直线平行于另外一个平面。

定理2
两个平行平面，分别和第三个平面相交，交线平行。

定理3
两个平面平行，和一个平面垂直的直线必垂直于另外一个平面。

〔断定定理1的逆定理〕
定理4
三个平行平面截两条直线，形成的对应线段成比例。

定理5
平行平面间的间隔处处相等。

定理6
经过平面外一点，有且只有一个平面与平面平行。

证明面面平行的所有条件
断定定理：一个平面内的两条相交直线和另一个平面平行，那么这两个平面平行。

性质定理：假如两个平行平面同时和第三个平面相交，那么它们的交线平行。

1、一个平面内的两条相交直线平行于另一个平面，则这两平面平行；
2、垂直于同一直线的两平面平行；
3、一个平面内的两条相交直线与另一个平面内的两条相交直线平行，则这两个平面平行。

两平面平行简介
两平面平行是两平面间的一种位置关系，如果两个平面没有公共点，则称这两
个平面有平行位置关系，简称两平面相互平行，一个平面称为另一个平面的平行平面。

平面与平面平行的性质定理
如果两个平行平面都和第三个平面相交，那么它们的交线平行，由两个平面平行，我们还有：
1、如果两个平面平行，那么其中一个平面内的直线平行于另一个平面；
2、和两个平行平面同时垂直的直线，叫做这两个平行平面的公垂线。

它夹在
这两个平行平面间的部分叫这两个平行平面的公垂线段。

公垂线段的长度叫做两个平行平面的距离。

注意：①两个平面平行，其中一个平面内的直线必平行于另一个平面。

但这两
个平面内的所有直线并不一定相互平行。

它们可能是平行直线，也可能是异面直线，但不可能是相交直线。

②两个平面平行的性质定理指出两个平面平行时所具有的性质：如果两个平面
平行同时与第三个平面相交，那么它们的交线平行。

③一条直线垂直于两个平行平面中的一个平面，它也垂直于另一个平面。