量子论习题
- 格式:ppt
- 大小:1.43 MB
- 文档页数:45

量子力学习题及解答第一章 量子理论基础1.1 由黑体辐射公式导出维恩位移定律:能量密度极大值所对应的波长m λ与温度T 成反比,即m λ T=b (常量);并近似计算b 的数值,准确到二位有效数字。
解 根据普朗克的黑体辐射公式dv e chv d kThv v v 11833-⋅=πρ, (1)以及 c v =λ, (2)λρρd dv v v -=, (3)有,118)()(5-⋅=⋅=⎪⎭⎫ ⎝⎛-=-=kThc v v ehc cd c d d dv λλλπλλρλλλρλρρ这里的λρ的物理意义是黑体内波长介于λ与λ+d λ之间的辐射能量密度。
本题关注的是λ取何值时,λρ取得极大值,因此,就得要求λρ 对λ的一阶导数为零,由此可求得相应的λ的值,记作m λ。
但要注意的是,还需要验证λρ对λ的二阶导数在m λ处的取值是否小于零,如果小于零,那么前面求得的m λ就是要求的,具体如下:01151186'=⎪⎪⎪⎭⎫⎝⎛-⋅+--⋅=-kT hc kThce kT hc ehcλλλλλπρ⇒ 0115=-⋅+--kThc ekThcλλ⇒ kThcekThc λλ=--)1(5 如果令x=kThcλ ,则上述方程为 x e x =--)1(5这是一个超越方程。
首先,易知此方程有解:x=0,但经过验证,此解是平庸的;另外的一个解可以通过逐步近似法或者数值计算法获得:x=4.97,经过验证,此解正是所要求的,这样则有xkhc T m =λ 把x 以及三个物理常量代入到上式便知K m T m ⋅⨯=-3109.2λ这便是维恩位移定律。
据此,我们知识物体温度升高的话,辐射的能量分布的峰值向较短波长方面移动,这样便会根据热物体(如遥远星体)的发光颜色来判定温度的高低。
1.2 在0K 附近,钠的价电子能量约为3eV ,求其德布罗意波长。
解 根据德布罗意波粒二象性的关系,可知E=hv ,λh P =如果所考虑的粒子是非相对论性的电子(2c E e μ<<动),那么ep E μ22= 如果我们考察的是相对性的光子,那么E=pc注意到本题所考虑的钠的价电子的动能仅为3eV ,远远小于电子的质量与光速平方的乘积,即eV 61051.0⨯,因此利用非相对论性的电子的能量——动量关系式,这样,便有ph=λnmm m E c hc E h e e 71.01071.031051.021024.1229662=⨯=⨯⨯⨯⨯===--μμ在这里,利用了m eV hc ⋅⨯=-61024.1以及eV c e 621051.0⨯=μ最后,对Ec hc e 22μλ=作一点讨论,从上式可以看出,当粒子的质量越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强;同样的,当粒子的动能越大时,这个粒子的波长就越短,因而这个粒子的波动性较弱,而粒子性较强,由于宏观世界的物体质量普遍很大,因而波动性极弱,显现出来的都是粒子性,这种波粒二象性,从某种子意义来说,只有在微观世界才能显现。



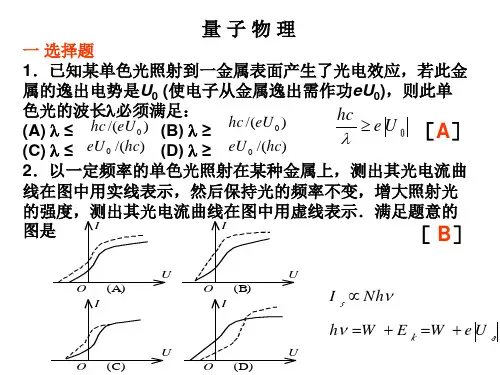
第 五 篇第 一 章 波粒二象性 玻尔理论一、选择题1. 已知某单色光照射到一金属表面产生了光电效应,若此金属的逸出电势是U 0 (使电子从金属逸出需作功eU 0),则此单色光的波长λ必须满足: [ A ] (A) 0eU hc ≤λ (B) 0eU hc≥λ (C) hc eU 0≤λ (D) hc eU 0≥λ解:红限频率与红限波长满足关系式hv 0=λhc=eU 0,即00eU hc =λ 0λλ≤才能发生光电效应,所以λ必须满足0eU hc≤λ 2. 在X 射线散射实验中,若散射光波长是入射光波长的1.2倍,则入射光光子能量0ε与散射光光子能量ε之比ε0为[ B ] (A) 0.8 (B) 1.2 (C) 1.6 (D) 2.0解: λεhc=,00λεhc=,02.1λλ= ,所以2.100==λλεε 3. 以下一些材料的功函数(逸出功)为铍 -----3.9 eV 钯 ---- 5.0 eV 铯 ---- 1.9 eV 钨 ---- 4.5 eV 今要制造能在可见光(频率范围为3.9×1014 Hz ~ 7.5×1014Hz)下工作的光电管,在这些材料中应选[ C ] (A) 钨 (B) 钯 (C) 铯 (D) 铍解:可见光的频率应大于金属材料的红限频率0νh , 才会发生光电效应。
这些金属的红限频率由A h =0ν可以得到:141934)(01086.101063.6106.15.4⨯=⨯⨯⨯=--钨ν(Hz)141934)(01007.121063.6106.10.5⨯=⨯⨯⨯=--钯ν(Hz) 141934) (01059.41063.6106.19.1⨯=⨯⨯⨯=--铯ν(Hz) 141934)(01041.91063.6106.19.3⨯=⨯⨯⨯=--铍ν(Hz)可见应选铯4. 以一定频率的单色光照射在某种金属上,测出其光电流曲线在图中用实线表示。
然后保持光的频率不变,增大照射光的强度,测出其光电流曲线在图中用虚线表示,满足题意的图是 [ B ]解:光的强度I=Nhv , 其中N 为单位时间内通过垂直于光线的单位面积的光子数。

精心整理量子物理习题解答习题17—1用频率为1ν的单色光照射某一金属时,测得光电子的最大初动能为E k 1;用频率为2ν的单色光照射另一种金属时,测得光电子的最大初动能为E k 2。
那么[ ](A)1ν一定大于2ν。
(B)1ν一定小于2ν。
(C)1ν一定等于2ν。
(D)1ν可能大于也可能小于2ν。
解:根据光电效应方程,光电子的最大初动能为由此式可以看出,E k 不仅与入射光的频率ν有关,而且与金属的逸出功A 有关,因此我们无法判习题 所以L (A)。
习题所以习题(A)1/4。
(B)1/8。
(C)1/16。
(D)1/32。
解:根据玻尔的理论,氢原子中电子的动能、角动量和轨道半径分别为mP E k 22= ; n P r L n == ;12r n r n = 所以电子的动能与量子数n 2成反比,因此,题给的两种情况下电子的动能之比12/42=1/16,所以我们选择答案(C)。
习题17—5在康普顿效应实验中,若散射光波长是入射光波长的1.2倍,则散射光光子能量ε与反冲电子动能E k 之比k E ε为[ ](A)2。
(B)3。
(C)4。
(D)5。
解:由康普顿效应的能量守恒公式可得所以,应该选择答案(D)。
习题17—6设氢原子的动能等于温度为T 的热平衡状态时的平均动能,氢原子的质量为m ,那么此氢原子的德布罗意波长为[ ](A)mkT h 3=λ。
(B)mkT h 5=λ。
(C)h mkT 3=λ。
(D)h mkT 5=λ。
把此式代入德布罗意公式有所以因此,应该选择答案(D)。
习题17—10氩(Z =18)原子基态的电子组态是:[ ] (A)1S 22S 83P 8(B)1S 22S 22P 63d 8 (C)1S 22S 22P 63S 23P 6(D)1S 22S 22P 63S 23P 43d 2解:对(A)示组态,既违反泡利不相容原理,也违反能量最小原理,是一个不可能的组态;对(B)示组态和(D)示组态均违反能量最小原理,也都是不可能组态。


吉林大学物理学院理论物理中心 高等量子力学习题† 量子力学中的对称性1、 试证明:若体系在线性变换Qˆ下保持不变,则必有0]ˆ,ˆ[=Q H 。
这里H ˆ为体系的哈密顿算符,变换Qˆ不显含时间,且存在逆变换1ˆ−Q 。
进一步证明,若Q ˆ为幺正的,则体系可能有相应的守恒量存在。
2、 令坐标系xyz O −绕z 轴转θd 角,试写出几何转动算符)(θd R zeG 的矩阵表示。
3、 设体系的状态可用标量函数描述,现将坐标系绕空间任意轴n G转θd 角,在此转动下,态函数由),,(z y x ψ变为),,(),()',','(z y x d n U z y x ψθψG =。
试导出转动算符),(θd n U G的表达式,并由此说明,若体系在转动),(θd n U G下保持不变,则体系的轨道角动量为守恒量。
4、 设某微观粒子的状态需要用矢量函数描述,试证明该粒子具有内禀自旋1=S 。
5、 证明宇称算符的厄米性和幺正性,并证明宇称算符为实算符。
6、 试证明幺正算符U 与复数共轭算符K 的乘积为反幺正算符。
7、 试证明自旋不为零的粒子的时间反演算符可表为K e T y S i π=−=。
8、 试讨论由时间反演不变性引起的Kramers 简并。
† 角动量理论1、 角动量算符可以从两个方面来定义,一种是按矢量算符三个分量所满足的对易关系定义,另一种是按坐标系转动时,态函数的变换规律来定义,试证明这两种定义是等价的。
2、 试证明任意个相互独立的角动量算符之和仍是角动量算符。
3、 定义角动量升降算符yx J i J J ˆˆˆ±=±,试利用升降算符讨论,对给定的角量子数j ,相应的磁量子数m 的取值范围。
4、 给出角量子数1=j 情况下,角动量平方算符及角动量各分量的矩阵表示。
5、 设总角动量算符21J J J G G G +=,1J G 、2J G相应的角量子数分别为1j 和2j ,试讨论总角动量量子数j 的取值情况。

量子力学练习题随着科学技术的不断进步,量子力学作为近代物理学的基石,在我们生活中扮演着越来越重要的角色。
量子力学的概念和理论模型不仅用于解释微观世界的现象,还应用于信息处理、材料科学等领域。
为了加深对量子力学的理解,本文将为读者提供一些量子力学练习题,请认真思考并尽力解答。
题目一:平面上的单粒子态考虑一个二维平面上的单粒子,其波函数为Ψ(x, y)。
假设该波函数可以展开为以下形式:Ψ(x, y) = A(xe^(-λx) + ye^(-λy))其中,A和λ均为实常数。
1. 请计算波函数Ψ(x, y)的归一化常数A。
2. 求解波函数Ψ(x, y)对应的概率密度函数|Ψ(x, y)|^2。
3. 计算算符x和y对该波函数的期望值<x>和<y>。
题目二:自旋1/2粒子的测量考虑一个自旋1/2粒子,其自旋算符的本征态为|+⟩和|-⟩,对应自旋向上和向下的状态。
现在进行如下测量:1. 如果对该粒子的自旋以z方向为测量方向,求测量得到自旋向上状态的概率。
2. 假设在z方向上测量得到自旋向上状态后,立即进行对z方向自旋的再次测量,求再次测量得到自旋向上状态的概率。
3. 如果对该粒子的自旋以任意方向为测量方向,求测量得到自旋向上状态的概率。
题目三:简谐振子的能量本征态考虑一个一维简谐振子,其能量本征态可由波函数Ψ_n(x)表示,n 为非负整数。
波函数Ψ_n(x)的表达式为:Ψ_n(x) = N_n H_n(x) e^(-x^2/2)其中,N_n为归一化常数,H_n(x)为Hermite多项式。
1. 请计算波函数Ψ_0(x)的归一化常数N_0。
2. 求解波函数Ψ_1(x)对应的薛定谔方程解,并给出其归一化常数N_1。
3. 计算简谐振子的能量本征值E_n,其中n = 0, 1, 2。
题目四:双缝干涉实验考虑一个双缝干涉实验,光源发射频率为f,波速为v。
光通过双缝后形成干涉条纹,条纹之间的间距为d。

现代物理(量⼦⼒学习题)思考题(程守诛江之永《普通物理学》)1两个相同的物体A 和B,具有相同的温度,如A 物体周围的温度低于A ,⽽B物休周围的温度⾼于B.试问:A 和B 两物体在温度相同的那⼀瞬间.单位时间内辐射的能量是否相等?单位时间内吸收的能量是否相等?2绝对⿊体和平常所说的⿊⾊物体有何区别?绝对⿊体在任何温度下,是否都是⿊⾊的?在同温度下,绝对⿊体和⼀般⿊⾊物休的辐出度是否⼀样? 3你能否估计⼈体热辐射的各种波长中,哪个波长的单⾊辐出度最⼤?4有两个同样的物体,⼀个是⿊⾊的,⼀个是⽩⾊的且温度相同.把它们放在⾼温的环境中,哪⼀个物体温度升⾼较快?如果把它们放在低温环境中.哪⼀个物体温度降得较快?5 若⼀物体的温度(绝对温度数值)增加⼀倍.它的总辐射能增加到多少倍? 6在光电效应的实验中,如果:(1)⼊射光强度增加1倍;(2)⼊射光频率增加1倍,按光⼦理论,这两种情况的结果有何不同?;7已知⼀些材料的逸出功如下:钽4.12eV ,钨4.50eV ,铝 4.20eV ,钡2. 50eV ,锂2. 30eV .试问:如果制造在可见光下⼯作的光电管,应取哪种材料?8在彩⾊电视研制过程中.曾⾯临⼀个技术问题:⽤于红⾊部分的摄像管的设计技术要⽐绿、蓝部分困难,你能说明其原因吗?·9光⼦在哪些⽅⾯与其他粒⼦(譬如电⼦)相似?在哪些⽅⾯不同? 10⽤频率为v 1的单⾊光照射某光电管阴极时,测得饱和电流为I 1,⽤频率为v 2的单⾊光以与v1的单⾊光相等强度照射时,测得饱和电流为I2,:若I2>I1,v 1和v 2的关系如何?11⽤频率为v1的单⾊光照射某光电管阴极时,测得光电⼦的最⼤动能为E K1 ;⽤频率为v 2的单⾊光照射时,测得光电⼦的最⼤动能为E k2 ,若E k1 >E k2,v 1和v 2哪⼀个⼤?12⽤可见光能否观察到康普顿散射现象?13光电效应和康普倾效应都包含有电⼦与光⼦的相互作⽤,这两过程有什么不同?14在康普顿效应中,什么条件下才可以把散射物质中的电⼦近似看成静⽌的⾃由电⼦?15在康普顿效应中,反冲电⼦获得的能量总是⼩于⼊射光⼦的能量这是否意味着⼊射光的光⼦分成两部分,其中的⼀部分被电⼦吸收.这与光⼦的粒⼦性是否⽭盾?16 (1) 氢原⼦光谱中.同⼀谱系的各相邻谱线的间隔是否相等?(2) 试根据氢原⼦的能级公式说明当量⼦数n 增⼤时能级的变化情况以及能级间的间距变化情况.17了由氢原⼦理论可知.当氢原⼦处于 n=4的激发态时,可发射⼏种波长的光?18如图所⽰.被激发的氢原⼦跃迁到低能级时,可发射波长为λ1、λ2、λ3的辐射.问三个波长之间的关系如何?19设实物粒⼦的质量为m, 速度为v, 由德布罗意公式mV h mc hv /,2==λ得 V c v /2=λλ根据Vv=得Vc=显然以上的结论是错误的,试问错误的根源何在?8-20为什么说不确定度关系与实验技术或仪器的改进⽆关?习题1、估测星球表⾯温度的⽅法之⼀是:将星球看成⿊体,测量它的辐射峰值波长。

量子物理课堂习题Lecture 1: 旧量子论1.求氘原子Hα线n=2到n=3的波数2.Ce的逸出功是1.9eV, 求阈值频率和波长3.对于氢原子、一次电离的氦离子He+和两次电离的锂粒子Li++,分别计算它们的:a)第一、第二波尔轨道半径及电子在这些轨道上的速度b)电子在基态的结合能c)第一激发态退激到基态所放光子的波长Lecture 2:波粒二象性不确定性原理=a(n=1,2,…, a 为弦长)。
按照“定态即驻波”的说1.已知琴弦振动的驻波条件为nλ2法,束缚在长宽高分别为a,b,c 的三维势箱中的粒子(质量为m)的定态能量取值是多少?2.一原子的激发态发射波长为600nm 的光谱线,测得波长的精度为∆λ/λ=10−7,试问该原子态的寿命为多长?3.1,3—丁二烯分子长度a≈7Å,试用测不准关系估计其基电子态能级的大小(量级)Lecture 3: 波函数薛定谔方程1.下列哪些函数不是品优函数,说明理由:f(x)=x2,e−|x|,sin(x),e−x22.试写出下列体系的定态薛定谔方程:(a)He 原子(b)H2 分子3.写出一个被束缚在半径为a的圆周上运动的粒子的Schrödinger 方程,并求其解Lecture 4: 势箱模型1.(2.7)Consider a particle with quantum number n moving in a one-dimensional box of lengthl.(a) Determine the probability of finding the particle in the left quarter of the box.(b)For what value of n is this probability a maximum?(c) What is the limit of this probability for n→∞?(d) What principle is illustrated in (c)?2.(2.17)A crude treatment of the pi electrons of a conjugated molecule regards theseelectrons as moving in the particle-in-a-box potential of Fig. 2.1, where the box length issomewhat more than the length of the conjugated chain. The Pauli exclusion principle(Chapter 10) allows no more than two electrons to occupy each box level. (These two haveopposite spins.) For 1,3-butadiene, CH2 =CHCH=CH2, take the box length as 7.0 Å and usethis model to estimate the wavelength of light absorbed when a p electron is excited from thehighest-occupied to the lowest-vacant box level of the molecular electronic ground state. The experimental value is 217 nm.3.(2.18) For the particle in a one-dimensional box of length 1, we could have put the coordinateorigin at the center of the box. Find the wave functions and energy levels for this choice of origin.4.试用一维势箱模型(6个电子)计算如下分子的电子光谱最大吸收波长(第一吸收峰)。
一.微观粒子的波粒二象性1、在温度下T=0k 附近,钠的价电子能量约为3电子伏特,求其德布罗意波长。
2、求与下列各粒子相关的德布罗意波长。
(1)能量为100电子伏特的自由电子;(2)能量为0.1电子伏特的自由中子;(3)能量为0.1电子伏特,质量为1克的自由粒子; (4)温度T=1k 时,具有动能kTE 23=的氦原子,其中k 为玻尔兹曼常数。
3、若电子和中子的德布罗意波长等于oA 1,试求它们的速度、动量和动能。
4、两个光子在一定条件下可以转化为正负电子对,如果两电子的能量相等,问要实现这种转化,光子的波长最大是多少?5、设一电子为电势差U 所加速,最后打在靶上,若电子的动能转化为一光子,求当这光子相应的光波波长分别为5000oA (可见光)o A 1(x 射线),oA001.0(γ射线)时,加速电子所需的电势差各是多少?二.波函数与薛定谔方程1、设粒子的归一化波函数为 ),,(z y x ϕ,求 (1)在),(dx xx +范围内找到粒子的几率;(2)在),(21y y 范围内找到粒子的几率; (3)在),(21x x 及),(21z z 范围内找到粒子的几率。
2、设粒子的归一化波函数为 ),,(ϕθψr ,求:(1)在球壳),(dr rr +内找到粒子的几率;(2)在),(ϕθ方向的立体角Ωd 内找到粒子的几率; 3、下列波函数所描述的状态是否为定态?为什么?(1)Eti ix Eti ix ex ex t x---+=ψ)()(),(211ψψ[])()(21x x ψψ≠(2)tE i t E i ex ex t x 21)()(),(2--+=ψψψ)(21E E ≠(3)EtiEti ex ex t x)()(),(3ψψ+=ψ-4、对于一维粒子,设 xp i o e xπψ21)0,(=,求 ),(t x ψ。
5、证明在定态中,几率密度和几率流密度均与时间无关。
6、由下列两个定态波函数计算几率流密度。
3.1幺正算符也有本征矢量。
证明幺正算符的本征值都是绝对值是1的复数;幺正算符的两个本征矢量,若所属本征值不同亦必正交。
证明: 设算符U为幺正算符,ψ为其任意本征矢量,u 为对应的本征值。
即ψψu U =则ψψψψψψψψu u U U U U *+===因0≠ψψ,所以1=*u u 即 1=u即证得幺正算符的本征值都是绝对值是1的复数。
设算符U 为幺正算符的两个本征值为1u 、2u ,对应的矢量分别为1ψ、2ψ,且21u u ≠。
则111ψψu U = 11111ψψu U =- 222ψψu U = 22211ψψu U =- 因为幺正算符1-+=U U则有21212121ψψψψψψu u U U *+==2121211ψψψψu u UU *+== 所以01212121=⎪⎪⎭⎫ ⎝⎛-**ψψu u u u 因为012121≠-**u u u u ,故021=ψψ,即 1ψ和2ψ正交。
即证得幺正算符的两个本征矢量,若所属本征值不同亦必正交。
3.2 投影于某一子空间的投影算符P ,既然是厄米算符,它的本征值是什么?有无简并?本证子空间是什么?解:投影于某一子空间的投影算符∑==mi iP 1,设全空间是n 维的,且n m <。
则本征值方程ψλψψ==∑=mi i iP 1⑴其中λ为本征值,ψ为相应的本征态。
则ψλψλψ22==P P ⑵ 由幺正算符等幂性P P =2得ψψP P =2 ⑶ 由⑴、⑵和⑶式得λλ=2,所以1=λ或0=λ。
即求得投影算符的本征值是1或0。
当1=λ时,本征失量是i ,其中m i ,2,1=。
所以是简并的,本征子空间S 是由这m 个基矢构成的矢量空间。
当0=λ时,本征矢量是与i 正交的矢量。
所以也是简并的,本征子空间是S 空间的补空间。
#练习3.3 证明若算符的本征值谱中有零本征值,则这个算符肯定没有逆。
证明:假设算符A 有逆,则在值域中取一任意|φ>,则定义域有|ψ>存在即ψφφ-==AA 1已知A的全部本征值和相应的本征矢量:i i i a A ψφ= i=1,2,3…,∴()ψψφ--==A a AA算符A 存在零本征值,即00=⇒=φa a∴对于任意本征矢量()ψφa A -≠与()ψφ-=A a 矛盾∴假设不成立,即算符的本征值谱中有零本征值,这个算符肯定没有逆。
量子力学 练习题1答案一。
基本概念及简要回答1. p 和 p是否相等?为什么?答:不相等。
因为p是动量 p r的本证态,而p是动量p r的本证态,实际上p与p r代表同一个态。
2. 判定下列符号中,哪些是算符?哪些是数?哪些是矢量?; )()(t t ; w v u ; w Fu ˆ。
答:是算符,)()(t t ,w Fˆ是数, w v u 是矢量。
3. 波函数的导数是否一定要连续?举例说明。
答:不一定。
例如,对于无限深势阱波函数中粒子波函数在全空间连续,但微商在0和a 点不连续。
4.为什么既不能把 波理解为‘粒子的某种实际结构,即把波包看作粒子’, 也不把 波理解为‘由大量粒子分布于空间而形成的波,即把波看作由粒子构成的’?答:自由粒子的物质波包必然要扩散,与实验矛盾。
所以不能‘把波包看作粒子’;另一方面,戴维逊-戈末实验表明电子的波动性不是很多电子在空间聚集在一起时才呈现的现象,单个电子就具有波动性,否则每次只有一个粒子,但长时间的衍射干涉就不会有干涉花样. 所以不能‘把波看作由粒子构成的’。
5. 设ˆˆA A ,ˆˆB B ,ˆˆ0A B ,。
试判断下列算符哪些是厄米算符,哪些不是。
(1)1ˆˆˆˆˆ()2F AB BA i; (2)ˆˆˆG AB ; (3)ˆˆˆC A iB ; (4)ˆˆˆDA B 。
解:(1)1ˆˆˆˆˆ()2F AB BA i,11ˆˆˆˆˆˆˆˆˆ()()22F B A A B AB BA i iˆˆFF ,即ˆF 为厄米算符。
(2)ˆˆˆG AB , ˆˆˆˆˆˆˆˆˆˆG AB B A BA AB G。
ˆG不是厄米算符。
(3)ˆˆˆC AiB ,ˆˆˆC A iBˆˆC C ,即ˆC 不是厄米算符。
(4)ˆˆˆD AB ,ˆˆˆˆˆD A B A BˆˆDD ,即ˆD 为厄米算符。
6. (9’) 指出下列使用的Dirac 符号那些是不正确的。
为什么?A.)(t ; B. )(x ; C.)(t ; D. ()r r rv; E.10; F. )'('x x x . 答:B ,E ,F 不正确。
量⼦⼒学习题第⼆章波函数与薛定谔⽅程(1)⼀、填空题1、在量⼦⼒学中,描述系统的运动状态⽤波函数()r ψ,⼀般要求波函数满⾜三个条件即有限性;连续性;单值性。
根据玻恩对波函数的统计解释,电⼦呈现的波动性只是反映客体运动的⼀种统计规律,称为概率波,波函数模的平⽅()2r ψ表⽰粒⼦在空间的⼏率分布,称为概率密度。
⽽()2r d ψτ表⽰在空间体积 dt 中概率,要表⽰粒⼦出现的绝对⼏率,波函数必须归⼀化。
2r 点处⼩体积元dτ内粒⼦出现的⼏率与波函数模的平⽅(|Ψ|2)成正⽐。
3、根据波函数的统计解释,dx t x 2),(ψ的物理意义为粒⼦在xdx 范围内的概率。
4、在量⼦⼒学中,描述系统的运动状态⽤波函数()r ψ,⼀般要求波函数满⾜三个条件即有限性;单值性;连续的。
5、波函数的标准条件为(1)波函数可归⼀化(2)波函数的模单值(3)波函数有限。
6、三维空间⾃由粒⼦的归⼀化波函数为()r pψ= ,()()=?+∞∞-*'τψψd r r p p见书P18 。
7、动量算符的归⼀化本征态=)(r p ψ,='∞τψψd r r p p )()(* 见书P18 。
8、按照量⼦⼒学理论,微观粒⼦的⼏率密度w = 见⽹页收藏,⼏率流密度= 。
9、设)(r ψ描写粒⼦的状态,2)(r ψ是概率波,在)(rψ中⼒学量F的平均值为F = 。
10、波函数ψ和ψc 是描写状态,δψi e 中的δi e 称为,δi e 不影响波函数ψ的归⼀化,因为。
11、定态是指的状态,束缚态是指的状态。
12、定态波函数的形式为。
13、)i exp()()iexp()(),(2211t Ex t E x t x-+-=ψψψ是定态的条件是,这时⼏率密度和都与时间⽆关。
14、波函数的统计解释 15.描述微观粒⼦状态的波函数ψ应满⾜的三个标准条件。
16、粒⼦作⾃由运动时,能量本征值是___ __。
17、已知()r V H +?-=2212?µ的本征函数为()r ψ,与它相应的本征值为E ,则()C r V H ++?-= 2222?µ(C 为常数)的本征函数为,本征值为。