(上海最好的高中物理讲义)匀变速直线运动中s=at2的讲解

2aTs=∆问题说明：在匀变速直线运动中，所有的公式都是四个未知数组成的，需要知道其中的三个，才可以求出另外一个，而2aTs=∆中，只有三个未知数，从运算量上来说，减少了；相应地需要的思考量就增加了。

因此这个公式主要用在填空题及选择题的运算，实验题中用得也不少，大的计算题则作为辅助手段来用。

类型一：基本应用（把握要点：相邻且相等）[例1]一物体做匀变速直线运动，第一个2秒内的位移是20米，第二个2秒内的位移是0米，求该运动的加速度为m/s2，初速度为m/s。

解析：相邻且相等的2秒内，由2aTs=∆得，a=(20-0)/(2*2)=5m/s2；由221att vso+=得初速度vo=5m/s。

类型二：变形应用说明：公式的要点是相邻且相等，而出题的要点则偏偏是偏开要点，而又可以用该公式去做。

与解方程类似，我们只会解一元一次方程，所以多元方程就消元，高次方程则降次，这里思路一样，将不相等转换成相等，将不相邻转换成相邻。

变形应用一：相等不相邻[例2]一物体做匀变速直线运动，第7秒内的位移比第3秒的位移多24米，则运动的加速度为m/s2。

解：匀变速直线运动中，第4秒比第3秒多s∆，第5秒比第4秒多s∆，依此可知，第7秒比第3秒多（7-3）个s∆。

由2aTs=∆知，42aT=24，则a=6m/s2易错点提醒：位移多24米，和位移的大小多24米是不一样的，矢量运算中一旦出现大小二字，方向要单独讨论。

变形应用二：相邻不相等[例3]一物体做匀变速直线运动总计5秒，前2秒位移为40米，后3秒的位移为135米，则运动的加速度为m/s2。

解：设物体第1秒的位移为S，则有2S+s∆=40 3S+9s∆=135解得s ∆=10 则a=10m/s 2。

(上述问题均可用2t v v =来做，这里提供一种思路)类型三：实验题（如何处理误差）[例4]某同学用题图所示装置测量重力加速度g,所用交流电频率为50 Hz.在所选纸带上取某点为0号计数点，然后每3个点取一个计数点，所以测量数据及其标记符号如图所示.该同学用两种方法处理数据(T 为相邻两计数点的时间间隔)：方法A ：由……，，取平均值g=8.667 m/s2; 方法B ：由取平均值g=8.673 m/s2.从数据处理方法看，在S 1、S 2、S 3、S 4、S 5、S6中，对实验结果起作用的，方法A 中有__________；方法B 中有___________.因此，选择方法_______（A 或B ）更合理，这样可以减少实验误差.本实验误差的主要来源有____________（试举出两条）.如果要求出编号为“4”的点时的速度正确的求法是v 4=____________（只要求用题中的字母写出表达式）.解析：在实验中，常常用2aT s =∆计算物体的加速度，但是由于实验误差，s ∆并不能完全相等，此时需要尽可能多的用到实验数据，减小误差。

匀变速直线运动两大推论从离地面高度为h 处有自由下落的甲物体，同时在它正下方的地面上有乙物体以初速度 竖直上抛，要使两物体在空中相 碰，则做竖直上抛运动物体的初速度v 0应满足什么条件？(不计空气阻力，两物体均看作质点)。

若要乙物体在下落过程中与甲物体相碰，则 应满足什么条 【例1】做匀变速直线运动的物体，在第一个3s 内的位移为 【例2 ＝2.0 m/s ， ＝ 时的 在第3 s 内通过的位移是4.5 m ，则它的加速度为 速度为( ) A ．1.5m/s B ．2.5m/s 2 C ．3.5m/sD ．4.5m/s1( ) 要使两物体在空中相 v 0 0件应满足什么条件？6m ，第一个5s 内的位移为15m ，则质点在t 4s A ．2.0 m/s 2 B ．0.5 m/s 2 C ．1.0 m/s D ．1.5 m/s 2【例3】自由下落的物体，在落地前最后1s 内下落了25m ，问 【例5】一辆汽车在平直的公路上做匀变速直线运动，该公路此物体是从离地面多高的地方开始下落的？(取g ＝ 每隔60米就有一电线杆，汽车通过第一根和第二根电 10m/s 2) 线杆用了5秒，通过第二根和第三根电线杆用了3秒｡ 求:汽车的加速度和经过这三根电线杆时的瞬时速度｡【例4】一物体做匀加速直线运动，在第1个t ，第末的速度是？【例6】做匀加速直线运动的物体，依次通过A 、B 、C 三点， 【例7】一列火车作匀变速直线运动驶来，一人在轨道旁观察 位移AB 等于BC ，物体在AB 段的平均速度为3m/s ，在 火车的运动，发现在相邻的两个10s 内，火车从他面前 BC 段的平均速度为6m/s ，那么物体在B 点的瞬时速度 分别驶过8节车厢和6节车厢，每节车厢长8m 。

求： 应为 ( ) A ．4 m/sB ．4.5 m/sC ．5 m/sD ．5.5 m/s2内位移为x 12个t 内位移为x 2，则物体在第1个t⑴火车的加速度a ； ⑵人开始观察时火车速度的大小。

2aTs=∆问题说明：在匀变速直线运动中，所有的公式都是四个未知数组成的，需要知道其中的三个，才可以求出另外一个，而2aTs=∆中，只有三个未知数，从运算量上来说，减少了；相应地需要的思考量就增加了。

因此这个公式主要用在填空题及选择题的运算，实验题中用得也不少，大的计算题则作为辅助手段来用。

类型一：基本应用（把握要点：相邻且相等）[例1]一物体做匀变速直线运动，第一个2秒内的位移是20米，第二个2秒内的位移是0米，求该运动的加速度为m/s2，初速度为m/s。

解析：相邻且相等的2秒内，由2aTs=∆得，a=(20-0)/(2*2)=5m/s2；由221att vso+=得初速度vo=5m/s。

类型二：变形应用说明：公式的要点是相邻且相等，而出题的要点则偏偏是偏开要点，而又可以用该公式去做。

与解方程类似，我们只会解一元一次方程，所以多元方程就消元，高次方程则降次，这里思路一样，将不相等转换成相等，将不相邻转换成相邻。

变形应用一：相等不相邻[例2]一物体做匀变速直线运动，第7秒内的位移比第3秒的位移多24米，则运动的加速度为m/s2。

解：匀变速直线运动中，第4秒比第3秒多s∆，第5秒比第4秒多s∆，依此可知，第7秒比第3秒多（7-3）个s∆。

由2aTs=∆知，42aT=24，则a=6m/s2易错点提醒：位移多24米，和位移的大小多24米是不一样的，矢量运算中一旦出现大小二字，方向要单独讨论。

变形应用二：相邻不相等[例3]一物体做匀变速直线运动总计5秒，前2秒位移为40米，后3秒的位移为135米，则运动的加速度为m/s2。

解：设物体第1秒的位移为S，则有2S+s∆=40 3S+9s∆=135解得s ∆=10 则a=10m/s 2。

(上述问题均可用2tv v =来做，这里提供一种思路)类型三：实验题（如何处理误差）[例4]某同学用题图所示装置测量重力加速度g,所用交流电频率为50 Hz.在所选纸带上取某点为0号计数点，然后每3个点取一个计数点，所以测量数据及其标记符号如图所示.该同学用两种方法处理数据(T 为相邻两计数点的时间间隔)：方法A ：由……，，取平均值g=8.667 m/s2;方法B ：由取平均值g=8.673 m/s2.从数据处理方法看，在S 1、S 2、S 3、S 4、S 5、S6中，对实验结果起作用的，方法A 中有__________；方法B 中有___________.因此，选择方法_______（A 或B ）更合理，这样可以减少实验误差.本实验误差的主要来源有____________（试举出两条）.如果要求出编号为“4”的点时的速度正确的求法是v 4=____________（只要求用题中的字母写出表达式）.解析：在实验中，常常用2aT s =∆计算物体的加速度，但是由于实验误差，s ∆并不能完全相等，此时需要尽可能多的用到实验数据，减小误差。

匀变速直线运动的规律匀变速直线运动公式1．常用公式有以下四个at v v t +=0 2021at t v s += as v v t 2202=- t v v s t 20+= 2．匀变速直线运动中几个常用的结论①Δs=aT 2，即任意相邻相等时间内的位移之差相等。

可以推广到s m -s n =(m-n)aT 2 ②ts v v v t t =+=202/，某段时间的中间时刻的即时速度等于该段时间内的平均速度。

22202/t s v v v +=，某段位移的中间位置的即时速度公式（不等于该段位移内的平均速度）。

可以证明，无论匀加速还是匀减速，都有2/2/s t v v <。

3．初速度为零（或末速度为零）的匀变速直线运动做匀变速直线运动的物体，如果初速度为零，或者末速度为零，那么公式都可简化为： gt v = ， 221at s = ， as v 22= ， t v s 2= 4．初速为零的匀变速直线运动①前1秒、前2秒、前3秒……内的位移之比为1∶4∶9∶……②第1秒、第2秒、第3秒……内的位移之比为1∶3∶5∶……③前1米、前2米、前3米……所用的时间之比为1∶2∶3∶……④第1米、第2米、第3米……所用的时间之比为1∶()12-∶（23-）∶…… 对末速为零的匀变速直线运动，可以相应的运用这些规律。

5．一种典型的运动经常会遇到这样的问题：物体由静止开始先做匀加速直线运动，紧接着又做匀减速直线运动到静止。

用右图描述该过程，可以得出以下结论： ①t s at a s ∝∝∝,1,1 ②221B v v v v === 6、解题方法指导：解题步骤：（1）确定研究对象。

（2）明确物体作什么运动，并且画出运动示意图。

（3）分析研究对象的运动过程及特点，合理选择公式，注意多个运动过程的联系。

（4）确定正方向，列方程求解。

（5）对结果进行讨论、验算。

解题方法：（1）公式解析法：假设未知数，建立方程组。

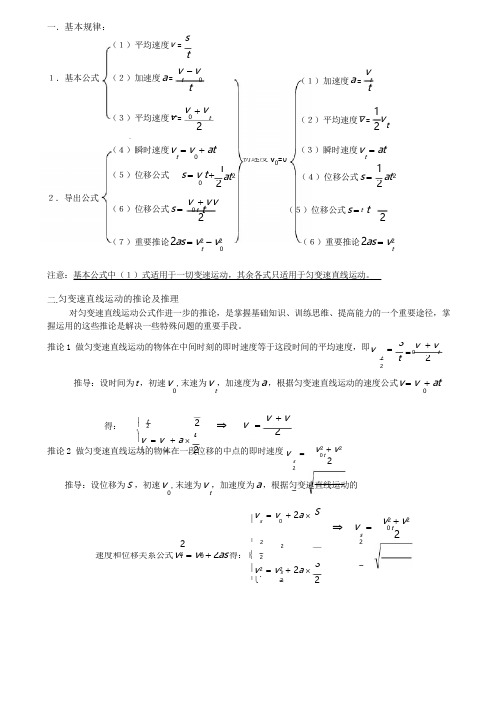
１．基本公式 （２）加速度 a = v - v初速度 v 0=0（５）位移公式 s = v t + 122推论 1 做匀变速直线运动的物体在中间时刻的即时速度等于这段时间的平均速度，即v= St 2⇒ v = v + v ⎪ t 2 ⎪ 2 ⎨ 2 ⎪v = v + a ⨯ t ⎪⎩ t2 ⎧2速度和位移关系公式 v 2 = v 2 + 2as 得： ⎪ 2⎪v 2 = v 2+ 2 a ⨯ S⎪⎩ t 22一．基本规律：（１）平均速度 v =stvt 0（１）加速度 a = ttt（３）平均速度 v = v 0 +v2t1（２）平均速度 v = v2 t（４）瞬时速度 v = v + at（３）瞬时速度 v = attt1at 2（４）位移公式 s = at 2２．导出公式（６）位移公式 s = v + v v0 t t （５）位移公式 s = t t2 2（７）重要推论 2as = v 2 - v 2t（６）重要推论 2as = v 2t注意：基本公式中（１）式适用于一切变速运动，其余各式只适用于匀变速直线运动。

二.匀变速直线运动的推论及推理对匀变速直线运动公式作进一步的推论，是掌握基础知识、训练思维、提高能力的一个重要途径，掌握运用的这些推论是解决一些特殊问题的重要手段。

t v + v = 0t2推导：设时间为 t ，初速 v ,末速为 v ，加速度为 a ，根据匀变速直线运动的速度公式 v = v + at0 t得：推论 2 做匀变速直线运动的物体在一段位移的中点的即时速度v=sv 2 + v 20 t22推导：设位移为 S ，初速 v ,末速为 v ，加速度为 a ，根据匀变速直线运动的0 t⎪vs = v 0+ 2 a ⨯2t 0 ⎨ s 2 S⇒ v =s2v 2 + v 20 t2经过第二个时间 t 后的速度为 v =2v +at ，这段时间内的位移为 S = v t + at 2 = v t + at 22 2 经过第三个时间 t 后的速度为 v =3v +at ，这段时间内的位移为 S = v t + at 2 = v t+ at 2 2 2 2 2 3 2 32 2 2 2t推论 3 做匀变速直线运动的物体,如果在连续相等的时间间隔 t 内的位移分别为 S 、 S 、 S …… S123n ，加速度为 a,则 ∆S =S 2- S 1 = S 3 - S 2= …… = S n - S推导：设开始的速度是 vn -1= at2经过第一个时间 t 后的速度为 v = v + a t ，这一段时间内的位移为 S = v t + 1 0 1 0 1 2 at 2，1 32 0 2 1 0 1 52 032…………………经过第 n 个时间 t 后的速度为 v =nv +at ，这段时间内的位移为 S =v t +1 a t 2 =v t + n 0 n n -1 02n -1 2at 2则 ∆S = S 2 - S 1 = S 3 - S 2 = …… = S n - Sn -1= at 2点拨：只要是匀加速或匀减速运动，相邻的连续的相同的时间内的位移之差，是一个与加速度 a 与时间 “有关的恒量”．这也提供了一种加速度的测量的方法： 即 a =∆S，只要测出相邻的相同时间内的位移之差 ∆S 和 t ，就容易测出加速度 a 。

高中物理知识点汇总：匀变速直线运动概念及公式物体在一条直线上运动，如果在相等的时间内速度的变化相等，这种运动就叫做匀变速直线运动。

也可定义为：沿着一条直线，且加速度不变的运动，叫做匀变速直线运动。

【概念及公式】沿着一条直线，且加速度方向与速度方向平行的运动，叫做匀变速直线运动。

如果物体的速度随着时间均匀减小，这个运动叫做匀减速直线运动。

如果物体的速度随着时间均匀增加，这个运动叫做匀加速直线运动。

s=1/2·at^2+vt=【v^2-v^2】/（2a)={【v（t）+v=v+at 其中a为加速度，v/2]·t利用速度公式v=v0+at，得s=[/2]·t=[v0+at/2]·t=v0·t+1/2·at^2⑵利用微积分的基本定义可知，速度函数（关于时间）是位移函数的导数，而加速度函数是关于速度函数的导数，写成式子就是ds/dt=v，dv/dt=a，d2s/dt2=a于是v=∫adt=at+v0，v0就是初速度，可以是任意的常数进而有s=∫vdt=∫（at+v0）dt=1/2at^2+v0·t+c，（对于匀变速直线运动），显然t=0时，s=0，故这个任意常数c=0，于是有s=1/2·at^2+v0·t这就是位移公式。

推论V^2－Vo^2=2ax平均速度=（初速度+末速度）/2=中间时刻的瞬时速度△X=aT^2（△X代表相邻相等时间段内位移差，T代表相邻相等时间段的时间长度）X为位移。

V为末速度Vo为初速度【初速度为零的匀变速直线运动的比例关系】⑴重要比例关系由Vt=at，得Vt∝t。

由s=^2③第1个t内、第2个t内、……、第n个t内（相同时间内）的位移之比xⅠ：xⅡ：xⅢ……：xn=1：3：5：……：（2n－1）。

推导：1/2·a^2：1/2·a（2t)^2－1/2·a^2：1/2·a （3t)^2－1/2·a（2t)^2④通过前1s、前2s、前3s……、前ns的位移所需时间之比t1：t2：……：tn=1：√2：√3……：√n。