轮子的受力分析过

6.6探究滑轮的作用【联系生活】滑轮是一个周边有槽，能够绕轴转动的小轮。

由可绕中心轴转动有沟槽的圆盘和跨过圆盘的柔索(绳、胶带、钢索、链条等)所组成的可以绕着中心轴旋转的简单机械叫做滑轮。

滑轮是一个周边有槽，能够绕轴转动的小轮。

由可绕中心轴转动有沟槽的圆盘和跨过圆盘的柔索（绳、胶带、钢索、链条等）所组成的可以绕着中心轴转动的简单机械叫做滑轮。

【教学目标】1．知识与技能目标：①知道定滑轮、动滑轮的作用，能区分定滑轮与动滑轮。

②会组装简单实验装置。

③会用杠杆平衡条件分析定滑轮和动滑轮的特点。

2.过程和方法①通过观察，了解滑轮的构造，培养学生观察能力。

②通过探究活动，培养学生研究物理的正确方法。

③通过实验现象和数据的分析，培养学生归纳总结、逻辑推理能力。

3．情感、态度和价值观目标：①通过“升旗”情景，对学生进行爱国主义的教育。

②通过探究活动，激发学生主动获取知识的兴趣和欲望，培养学生乐于探索并善于探索的学习品质。

③通过小组间交流与合作，培养学生团结合作的精神；在定、动滑轮学习的过程中，培养学生发现问题、提出问题、用已知的知识解决问题的能力。

教学重点和难点重点：定滑轮、动滑轮的特点和工作原理。

难点：动滑轮的支点和它的工作原理。

【学习目标】1、理解定滑轮、动滑轮特点、实质及其作用；2、理解滑轮组的作用及滑轮组的装配图。

【要点梳理】要点一、动滑轮和定滑轮在工作过程中，轴的位置固定不动的滑轮叫做定滑轮；在工作过程中，轴的位置随物体移动的滑轮叫做动滑轮。

要点诠释：1、定滑轮：如下图甲所示，我们可把一条直径看成杠杆，圆心就是杠杆的支点，因此，定滑轮实质是等臂杠杆。

定滑轮的特点是它的转轴（支点）不随货物上下移动。

2、动滑轮，如下图乙所示，特点是它的转动轴会随物体上下移动，它实质是动力臂为阻力臂2倍的省力杠杆，它的转动轴是阻力作用点。

3、定滑轮和动滑轮的作用使用定滑轮虽然不能省力，但可以改变用力方向，给工作带来方便。

作图题11 滑轮组作图一．作图技巧滑轮组绕线作图（1）绳子段数n 的计算方法：①距离关系确定:n ＝Sh(S 为绳端移动距离，h 为重物移动距离）；②力关系确定：F Gn 总. （2）找“起点”：根据“奇动偶定"的原则确定绳子的起点位置，即若n 为偶数，绳子从定滑轮绕起，若n 为奇数，绳子从动滑轮绕起。

二．真题精练1.(2020年西藏中考真题）如图所示，一物体静止在斜面上，图中已经画出了支持力的示意图，请画出物体受到的重力与摩擦力的示意图.【答案】 解：如图所示：【考点】重力示意图，摩擦力的示意图【解析】【解答】重力的方向始终是竖直向下的,物体受到的静摩擦力的方向与物体运动趋势的方向相反,如下图所示：【分析】物体受到的重力竖直向下;物体受到的摩擦力和物体相对运动方向相反.2.（2020年南京中考真题）如图（a)所示，空缆车随缆绳做匀速直线运动，在图（b）中画出缆车的轿厢（以方框表示）受力示意图（不计空气阻力)。

【答案】解：如图所示：【考点】弹力，重力及其大小的计算【解析】【解答】空缆车随缆绳做匀速直线运动，则轿厢也是做匀速直线运动,受力平衡，受到竖直向下的重力G和竖直向上的拉力F的作用，这两个力大小相同，作用点在轿厢的中心,示意图如图所示：【分析】作重力的示意图，力的作用点在物体几何中心上,方向竖直向下，重力用字母G表示，作绳子拉力的示意图，力的作用点在接触点上，方向指向绳子收缩的方向,用字母F表示。

3。

（2020年连云港中考真题）如图所示,物体A放在B上，在水平拉力F作用下一起向右做匀速直线运动，不计空气阻力，画出物体A的受力示意图。

【答案】解:如图所示;【考点】力的三要素及力的示意图，重力示意图【解析】【解答】物体A放在B上,在水平拉力F作用下一起向右做匀速直线运动，物体A处于平衡状态,A受到重力和支持力,从物体A的重心沿竖直向下和竖直向上分别画出重力和支持力的示意图,如图所示：【分析】物体受到的重力竖直向下,支持力和支撑面垂直.4。

难点之三：圆周运动的实例分析一、难点形成的原因1、对向心力和向心加速度的定义把握不牢固，解题时不能灵活的应用。

2、圆周运动线速度与角速度的关系及速度的合成与分解的综合知识应用不熟练，只是了解大概，在解题过程中不能灵活应用；3、圆周运动有一些要求思维长度较长的题目，受力分析不按照一定的步骤，漏掉重力或其它力，因为一点小失误，导致全盘皆错。

4、圆周运动的周期性把握不准。

5、缺少生活经验，缺少仔细观察事物的经历，很多实例知道大概却不能理解本质，更不能把物理知识与生活实例很好的联系起来。

二、难点突破（1）匀速圆周运动与非匀速圆周运动a.圆周运动是变速运动，因为物体的运动方向（即速度方向）在不断变化。

圆周运动也不可能是匀变速运动，因为即使是匀速圆周运动，其加速度方向也是时刻变化的。

b.最常见的圆周运动有：①天体（包括人造天体）在万有引力作用下的运动；②核外电子在库仑力作用下绕原子核的运动；③带电粒子在垂直匀强磁场的平面里在磁场力作用下的运动；④物体在各种外力（重力、弹力、摩擦力、电场力、磁场力等）作用下的圆周运动。

c.匀速圆周运动只是速度方向改变，而速度大小不变。

做匀速圆周运动的物体，它所受的所有力的合力提供向心力，其方向一定指向圆心。

非匀速圆周运动的物体所受的合外力沿着半径指向圆心的分力，提供向心力，产生向心加速度；合外力沿切线方向的分力，产生切向加速度，其效果是改变速度的大小。

例1：如图3-1所示，两根轻绳同系一个质量m=0.1kg 的小球，两绳的另一端分别固定在轴上的A 、B 两处，上面绳AC 长L=2m ，当两绳都拉直时，与轴的夹角分别为30°和45°，求当小球随轴一起在水平面内做匀速圆周运动角速度为ω=4rad/s 时，上下两轻绳拉力各为多少？ 【审题】两绳张紧时，小球受的力由0逐渐增大时，ω可能出现两个临界值。

【解析】如图3-1所示，当BC 刚好被拉直，但其拉力T 2恰为零，设此时角速度为ω1，AC 绳上拉力设为T 1，对小球有：mg T =︒30cos 1 ①30sin L ωm =30sin T AB 211②代入数据得： s rad /4.21=ω，要使BC 绳有拉力，应有ω>ω1，当AC 绳恰被拉直，但其拉力T 1恰为零，设此时角速度为ω2，BC 绳拉力为T 2，则有mg T =︒45cos 2 ③T 2sin45°=m 22ωL AC sin30°④代入数据得：ω2=3.16rad/s 。

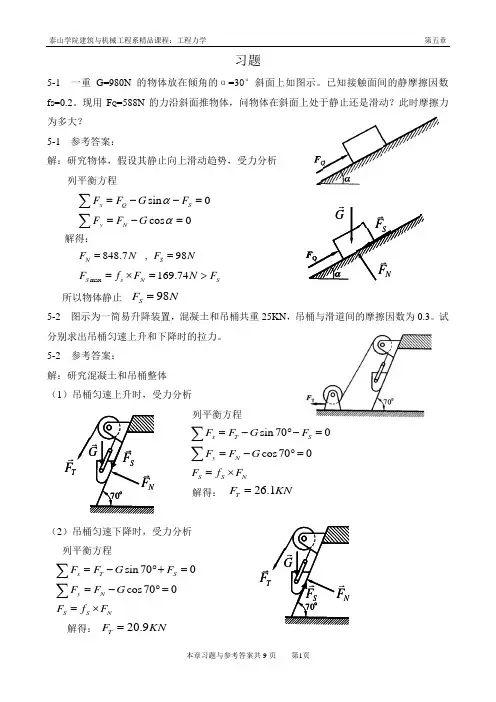
习题5-1 一重G=980N 的物体放在倾角的α=30°斜面上如图示。

已知接触面间的静摩擦因数fs=0.2。

现用F Q =588N 的力沿斜面推物体，问物体在斜面上处于静止还是滑动？此时摩擦力为多大？ 5-1 参考答案：解：研究物体，假设其静止向上滑动趋势，受力分析 列平衡方程解得：所以物体静止5-2 图示为一简易升降装置，混凝土和吊桶共重25KN ，吊桶与滑道间的摩擦因数为0.3。

试分别求出吊桶匀速上升和下降时的拉力。

5-2 参考答案：解：研究混凝土和吊桶整体 （1）吊桶匀速上升时，受力分析列平衡方程解得：（2）吊桶匀速下降时，受力分析列平衡方程解得： S F GNF sin 0cos 0x Q S yN F F G F FF G αα=--==-=∑∑848.7,98N S F N F N==max 169.74S s N SF f F N F =⨯=>98S F N =SF NF TF GS F NF TF Gsin 700cos700x T S yN S S NFF G F FF G F f F =-︒-==-︒==⨯∑∑26.1T F KN=20.9TF KN=sin 700cos700x T S yN S S N F F G F FF G F f F =-︒+==-︒==⨯∑∑5-3 已知某物块的质量，m=300kg ，被力Fp 压在铅直表面上。

物块与墙面间的静摩擦因数fs=0.25，试求保持物块静止的Fp 值的范围。

5-3 参考答案： 解：研究物块（1）物块上升趋势时，受力分析列平衡方程解得： （2）物块下滑趋势时，受力分析列平衡方程解得：5-4 图示为一重为G 的轮子。

已知轮子与墙面和地面间的静摩擦因数均为fs ，问轮上力偶M 为多大才能驱动轮子。

5-4 参考答案： 解：研究轮子，受力分析列平衡方程解得：505y P S x N P S S NF FG F F F F F f F =--==-⨯==⨯∑∑max 13148P F N=GS F NF GSF NF 0505y P S x N P S S NF FG F F F F F f F =-+==-⨯==⨯∑∑min4383P F N=438313148P N F N<<2N F 2S F 1N F 1S F ()21212221122000xN S yS N N iN S S S N S S N F F F F F F G M F M F r Fr F f F F f F =-==+-==-⨯-⨯==⨯=⨯∑∑∑()()211S S f G r f M f ⋅⋅+=+5-5 图示直杆质量为35 kg ，问多少的力Fp 才能使其移动？已知接触面间的静摩擦因数均 为0.3。

12.2 滑轮（解析版）考点1 滑轮及其工作特点（1）滑轮定义：周边有槽，中心有一转动的轮子叫滑轮。

因为滑轮可以连续旋转，因此可看作是能够连续旋转的杠杆，仍可以用杠杆的平衡条件来分析；（2）滑轮分类：定滑轮和动滑轮；定滑轮工作特点：（1）定滑轮使用时，滑轮的位置固定不变；定滑轮实质是等臂杠杆，不省力也不费力，但可以改变作用力方向。

（2）定滑轮的特点：通过定滑轮来拉钩码并不省力，通过或不通过定滑轮，弹簧测力计的读数是一样的，可见，使用定滑轮不省力但能改变力的方向。

在不少情况下，改变力的方向会给工作带来方便；（3）定滑轮的原理：定滑轮实质是个等臂杠杆，动力臂L 1、阻力臂L 2都等于滑轮半径，根杠杆平衡条件也可以得出定滑轮不省力的结论。

动滑轮工作特点：（1）动滑轮使用时，滑轮随重物一起移动；动滑轮实质是动力臂为阻力臂二倍的杠杆，省12力，多费1倍距离；典例分析＋变式训练考点直击（2）动滑轮的特点：使用动滑轮能省一半力，费距离；这是因为使用动滑轮时，钩码由两段绳子吊着，每段绳子只承担钩码重的一半。

使用动滑轮虽然省了力，但是动力移动的距离大于钩码升高的距离，即费了距离；（3）动滑轮的原理：动滑轮实质是个动力臂（L1）为阻力臂（L2）二倍的杠杆。

【典例1】（•阿荣旗二模）用定滑轮拉物体，不计摩擦，当沿不同方向将物体拉起时，拉力分别为F1、F2、F3，如图所示，则这三个力之间的大小关系正确的是（ ）A．F1＜F2＜F3B．F1＞F2＞F3C．F1＝F2＝F3D．无法判断【答案】C。

【分析】要解答本题需掌握：定滑轮实质上是一等臂杠杆，只改变力的方向，而不省力。

【解答】解：因为定滑轮相当于一个等臂杠杆，只能改变力的方向，而不省力，故在不计摩擦的情况下，定滑轮拉同一重物G，沿三个不同方向，用的拉力大小相等，即F1、F2、F3都等于物体的重力。

故A、B、D错误。

故选：C。

【典例2】（春•兴庆区期末）如图所示，通过动滑轮匀速提起重物G时，向三个方向拉动的力分别为F1、F2、F3，则这三个力大小关系是（ ）A．F1最大B．F2最大C．F3最大D．一样大【答案】C。

轮⼦的受⼒分析教程9：轮⼦的受⼒分析问题阐述下⾯所⽰为轮⼦的2D平⾯图，其中列出了该轮的基本尺⼨（单位为毫⽶）。

现要分析该轮仅承受绕Y轴旋转⾓速度的作⽤下，轮的受⼒及变形情况。

所给条件已知⾓速度为525rad/s，材料的弹性模量为200GPa，泊松⽐为0.3，密度为7.5g/mm3。

根据该轮的对称性，在分析时只要分析其中的⼀部分即可，即取模型的⼗六分之⼀。

交互式的求解过程1．定义单元类型和材料特性1.1 定义单元类型1．Main Menu：Preprocessor→Element Type→Add/Edit/Delete2．按下Element Type窗⼝内的Add按钮。

3．在单元类型库中，选择左侧列表中的SOLID单元家族，及右侧列表中Brick 8node 45类型。

4．按下Apply按钮完成选择。

5．在单元类型库中，选择左侧列表中的SOLID单元家族，及右侧列表中Brick 20node 95类型。

6．按下OK按钮完成选择。

7．按下Close按钮关闭Element Type窗⼝。

1.2 定义材料特性1．Main Menu：Preprocessor→Material Props→Material Models。

2．在材料定义窗⼝内选择：Structural→Linear→Elastic→Isotropic。

3．在EX后的⽂本框内输⼊数值2e5作为弹性模量。

在PRXY 后的⽂本框内输⼊数值0.3作为泊松⽐。

4．按下OK按钮完成定义。

5．在材料定义窗⼝内选择：Structural→Density，在出现的对话框中输⼊DENS=7.5e-9作为密度。

6．按下OK按钮完成定义。

2. 建⽴2D模型2.1 ⽣成矩形⾯1．Main Menu：Preprocessor→Modeling→Create→Areas→Rectangle→By Dimension。

2．在出现的对话框中分别输⼊：X1=25.4，X2=38.1，Y1=0，Y2=127。

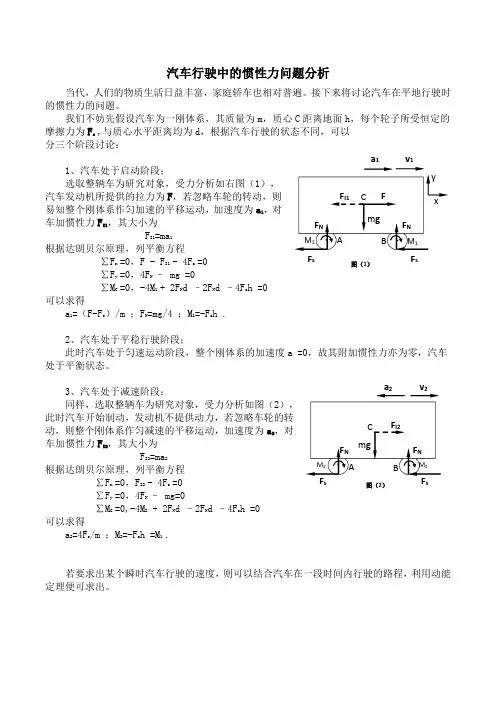
汽车行驶中的惯性力问题分析当代，人们的物质生活日益丰富，家庭轿车也相对普遍。

接下来将讨论汽车在平地行驶时的惯性力的问题。

我们不妨先假设汽车为一刚体系，其质量为m ，质心C 距离地面h ，每个轮子所受恒定的摩擦力为F s ,与质心水平距离均为d ，根据汽车行驶的状态不同，可以分三个阶段讨论：1、汽车处于启动阶段； 选取整辆车为研究对象，受力分析如右图（1），汽车发动机所提供的拉力为F ，若忽略车轮的转动，则易知整个刚体系作匀加速的平移运动，加速度为a 1，对车加惯性力F I1，其大小为 F I1=ma 1 根据达朗贝尔原理，列平衡方程∑F x =0，F - F I1 - 4F s =0 ∑F y =0，4F N – mg =0∑M C =0，-4M 1 + 2F N d –2F N d –4F s h =0可以求得a 1=（F-F s ）/m ；F N =mg/4 ；M 1=-F s h .2、汽车处于平稳行驶阶段；此时汽车处于匀速运动阶段，整个刚体系的加速度a =0，故其附加惯性力亦为零，汽车处于平衡状态。

3、汽车处于减速阶段；同样，选取整辆车为研究对象，受力分析如图（2），此时汽车开始制动，发动机不提供动力，若忽略车轮的转动，则整个刚体系作匀减速的平移运动，加速度为a 2，对车加惯性力F I2，其大小为 F I2=ma 2 根据达朗贝尔原理，列平衡方程∑F x =0，F I2 - 4F s =0 ∑F y =0，4F N – mg=0∑M C =0,-4M 2 + 2F N d –2F N d –4F s h =0可以求得a 2=4F s /m ；M 2=-F s h =M 1 .若要求出某个瞬时汽车行驶的速度，则可以结合汽车在一段时间内行驶的路程，利用动能定理便可求出。

F I1 a 1 m g F s F s F N F N v 1图（1）F C A B M 1M 1y F I2 m g a 2 v 2 C B A F N F s F s 图（2）M 2 M 2 F N。

对于轮子爬台阶的问题。

使用Adams分析，并说明添加扭矩与添加旋转速度驱动的分别。

轮子爬台阶过程：轮子本身有扭矩，使轮子对台阶有作用力。

台阶对轮子也产生反作用力，主要包括摩擦力和支持力。

如果台阶的摩擦系数足够大，那么台阶能产生的摩擦力大小就等于轮子受到的扭矩除以轮子的半径。

对轮子受力分析以及计算如下图所示。

我们需要爬的台阶高度是10mm。

轮子直径125mm。

能够看出，轮子想要爬10mm的台阶，扭矩需要达到1528Nmm。

问题说明：在Adams仿真过程中，发现用很小的扭矩（100Nmm）就能使轮子越过台阶（此时轮子和台阶的初始位置有一定距离）当我不断减小轮子和台阶的初始距离时，发现所需要的扭矩越来越大。

当轮子和台阶初始位置如图片所示。

则需要很大的扭矩，甚至大于1528Nmm。

这是为什么呢？原因分析：首先，当轮子和台阶有距离时，轮子运动到图片位置时已经有速度了。

此时轮子是依靠惯性和速度滚上台阶。

所以即使扭矩很小也能爬上台阶。

其次，当轮子和台阶初始位置就如图片所示，几乎接触。

此时即使很大扭矩，轮子也不能越上台阶。

这是由于台阶的摩擦系数小，已经不能提供足够的牵引力了。

通过实验发现，此时如果提高台阶与轮子的摩擦系数，就能够使轮子越上台阶。

后言：提高摩擦系数虽然能提高轮子爬台阶能力，但是与实际情况相悖，没有实际意义。

那么针对轮子爬台阶的问题，我得出的结论是，当摩擦系数一定时，轮子直径一定时，其能爬的台阶高度是一定的，即使增大扭矩，也不能使其越过台阶。

当然这是理想状态。

实际中，轮子有速度和惯性，这些都有利于轮子过障。

以上所得结论均是针对驱动轮而言。

非驱动的轮的情况较简单，不做详述。

QQQ~。

车轮问题摘要:在日常生活中，自行车通常是有三种类型的车轮，而在此问题我们主要研究的是其中两种类型，一种是由金属辐条组成，一种是由实体圆盘组成的。

他们各自也有各自的优势，金属辐条的通常较轻，实体圆盘更符合动力学原理。

对于一场自行车的公路比赛而言，天气，山丘的数量和陡度，风速等对比赛都有一些决定性影响，当然选择相应的轮胎也就至关重要。

对此我们主要需要研究的问题是在圆盘所需功率小于辐条所需功率时，风速的大小在不同坡度的情况下。

从而我们需要去提供一个表格关于风速和坡度的表格。

在研究整个问题中，首先是对给出的条件和关键词的反复理解和讨论。

任务一中，我们主要从“power”功率入手，由功率和力、速度之间的一个关系将其与风速联系起来，当然，这里的速度是车速与风速之间的一个相对运动速度。

然后开始对人和车体进行受力分析，分析其所受到的阻力，以及向前运动的动力。

我们采用了物理里的受力分析，牛顿第二定律，功率公式以及查阅文献资料等方法，并且排除了其他的一些干扰因素，在根据公式建立数学模型。

在模型的求解过程中，通过各类参考文献以及资料调查得出的各类参数，以及MATLAB 软件编程得出速度的一个范围值。

从而在根据这个速度是相对速度，从而求解出风速在任务二中，我们主要是需要我们自己设计一条路线，在任务一的基础下，比较不同选轮的比赛成绩。

根据文献资料统计我们得出运动员骑行时所提供的功率，并通过任务一中的功率公式得出其速度，在通过位移公式得出比赛时间，从而得到比赛成绩，进一步验证了我们任务一的结论。

在任务三中，我们需要判断一下我们任务一提供的表格是否是选车轮配置的一个充分条件，并且举出实际的例子来验证。

我们主要通过固定其他的一些因素和改变动摩擦因素来计算运动员消耗的体能。

运用到了物理学里的功能关系公式，从而得出改变其他因素对比赛的影响，证明到我们的任务一得出表格不是选择车轮的一个充分条件条件。

在这种情况下，我们求解出来的风速不会是一个确值，而只是一个范围。