初中一对一精品辅导讲义:圆与圆的位置关系.docx
- 格式:docx
- 大小:148.60 KB
- 文档页数:8
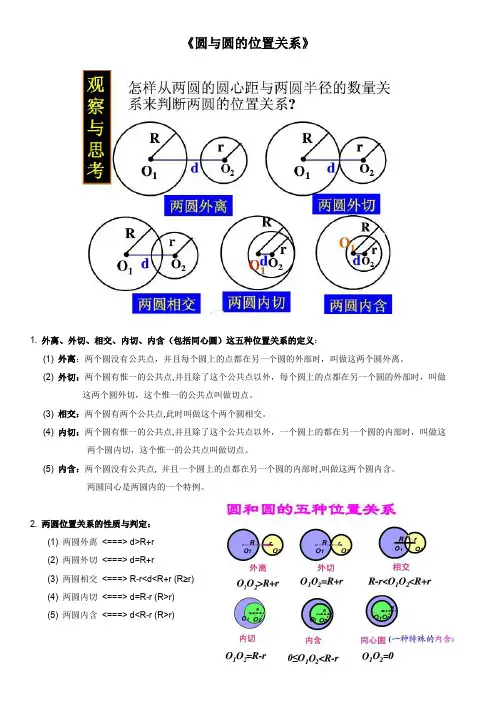
《圆与圆的位置关系》1. 外离、外切、相交、内切、内含(包括同心圆)这五种位置关系的定义:(1) 外离:两个圆没有公共点,并且每个圆上的点都在另一个圆的外部时,叫做这两个圆外离。
(2) 外切:两个圆有惟一的公共点,并且除了这个公共点以外,每个圆上的点都在另一个圆的外部时,叫做这两个圆外切,这个惟一的公共点叫做切点。
(3) 相交:两个圆有两个公共点,此时叫做这个两个圆相交。
(4) 内切:两个圆有惟一的公共点,并且除了这个公共点以外,一个圆上的都在另一个圆的内部时,叫做这两个圆内切,这个惟一的公共点叫做切点。
(5) 内含:两个圆没有公共点, 并且一个圆上的点都在另一个圆的内部时,叫做这两个圆内含。
两圆同心是两圆内的一个特例。
2. 两圆位置关系的性质与判定:(1) 两圆外离<===> d>R+r(2) 两圆外切<===> d=R+r(3) 两圆相交<===> R-r<d<R+r (R≥r)(4) 两圆内切<===> d=R-r (R>r)(5) 两圆内含<===> d<R-r (R>r)3. 相切两圆的性质:如果两个圆相切,那么切点一定在连心线上。
4. 相交两圆的性质:相交两圆的连心线垂直平分公共弦。
随堂练习: 1、已知⊙O 1和⊙O 2的半径分别为1和4,如果两圆的位置关系为相交,那么圆心距O 1O 2的取值范围在数轴上表示正确的是2、已知相交两圆的半径分别为5cm 和4cm ,公共弦长为6cm ,则这两个圆的圆心距是_____________.A BB . 3 1 0 2 4 5 D .3 1 0 245 A . 3 1 0 2 4 5 C .3、已知ABC △的三边分别是a b c ,,,两圆的半径12r ar b ==,, 圆心距d c =,则这两个圆的位置关系是 .4、如图3,⊙ABC 三边与⊙O 分别切于D ,E ,F ,已知AB=7cm ,AC=5cm ,AD=2cm ,则BC=______.5、两圆的圆心坐标分别是(,0)和(0,1),它们的半径分别是3和5,则这两个圆的位置关系是( )A .相离B .相交C .外切D .内切6、已知⊙O 1和⊙O 2的半径分别为1和5,圆心距为3,则两圆的位置关系是( )A .相交B .内含C .内切D .外切7、 如图,施工工地的水平地面上,有三根外径都是1m 的水泥管,两两相切地堆放在一起,其最高点到地面的距离是 .8、一个等腰梯形的高恰好等于这个梯形的中位线.若分别以这个梯形的上底和下底为直径作圆,这两个圆的位置关系是( )A .相离B .相交C .外切D .内切9、三角形三边长分别为5厘米、12厘米、13厘米,以三角形三个顶点为圆心的三个圆两两外切,则此三个圆的半径分别为 .10、两圆半径之比为3:2,当此两圆外切时,圆心距是10cm ,那么,当此两圆内切时,其圆心距为( )A .大于2cm 且小于6cmB .小于2cmC .等于2cmD .非以上取值范围11、已知⊙O 1、⊙O 2的半径分别为6和3,O 1、O 2的坐标分别是(5,0)和(0,6),则两圆的位置关系是( )A .相交B .外切C .内切D .外离12、R 、r 是两圆的半径(R >r ),d 是两圆的圆心距,若方程x 2-2Rx +r 2=d (2r -d )有等根,则以R 、r 为半径的两圆的位置关系是( )A .外切B .内切C .外离D .相交【例4】已知两圆半径分别为2和3,圆心距为d ,若两圆没有公共点,则下列结论正确的是( )A .01d <<B .5d >C .01d <<或5d >D .01d <≤或5d >【例5】已知⊙A 、⊙B 相切,圆心距为10cm ,其中⊙A 的半径为4cm ,求⊙B 的半径.3【例6】定圆O 的半径是4cm ,动圆P 的半径是1cm .当两圆相切时,点P 与点O 的距离是多少?点P 可以在什么样的线上移动?【例7】如图,AB 既是⊙C 的切线也是⊙D 的切线,⊙C 与⊙D 相外切,⊙C 的半径r=1,⊙D 的半径R=3, 求四边形ABCD 的面积。

圆与圆的位置关系(解析版)圆与圆的位置关系(解析版)圆与圆的位置关系是几何学中常见的问题。
在解析几何中,我们可以通过方程和图形的分析来确定两个圆之间的位置关系。
本文将详细介绍圆与圆的位置关系及其解析方法。
I. 两个圆的位置关系当给定两个圆的方程时,我们可以通过以下几种情况来判断它们的位置关系:1. 相离(disjoint)如果两个圆不相交,它们互相分离,也就是说没有公共点。
我们可以通过计算它们的半径之和和两个圆心之间的距离来判断。
如果半径之和小于圆心之间的距离,即 r1 + r2 < d,那么两个圆相离。
2. 外切(tangent exterior)如果两个圆的外部只有一个公共点,我们称它们相切于外部。
这意味着两个圆心之间的距离等于它们的半径之和,并且没有其他公共点。
我们可以通过计算两个圆心之间的距离和两个圆的半径之和来判断。
如果半径之和等于圆心之间的距离,即 r1 + r2 = d,那么两个圆相切于外部。
3. 内切(tangent interior)如果两个圆的内部只有一个公共点,我们称它们相切于内部。
这意味着两个圆的半径之差等于它们的圆心之间的距离,并且没有其他公共点。
我们可以通过计算两个圆的半径之差和两个圆心之间的距离来判断。
如果圆心之间的距离等于半径之差,即 d = |r1 - r2|,那么两个圆相切于内部。
4. 相交(intersect)如果两个圆有两个公共点,我们称它们相交。
这意味着两个圆心之间的距离小于半径之和,并且有两个公共点。
我们可以通过计算两个圆心之间的距离和两个圆的半径之和来判断。
如果半径之和大于圆心之间的距离,即 r1 + r2 > d,那么两个圆相交。
II. 解析方法在解析几何中,我们可以利用两个圆的方程来求解它们的位置关系。
假设第一个圆的方程为(x - h1)^2 + (y - k1)^2 = r1^2,第二个圆的方程为(x - h2)^2 + (y - k2)^2 = r2^2,其中(h1, k1)和(h2, k2)分别代表两个圆的圆心坐标,r1和r2分别代表两个圆的半径。


3·6圆和圆的位置关系1.圆与圆的五种位置关系:(1)外离:两个圆没有公共点,并且每一个圆上的点都在另一个圆的外部;(2)外切:两个圆有唯一公共点,除公共点外一个圆上的点都在另一个圆的外部;(3)相交:两个圆有两个公共点,一个圆上的点有的在另一个圆的外部,有的在另一个圆的内部;(4)内切:两个圆有一个公共点,除公共点外,⊙O2上的点在⊙O1的内部;(5)内含:两个圆没有公共点,⊙O2上的点都在⊙O1的内部.外离和内含都没有公共点;外切和内切都有一个公共点,相交有两个公共点.因此只从公共点的个数来考虑,可分为相离、相切、相交三种.(2)相交2.两圆相内切或外切时,两圆的连心线一定经过切点,都是轴对称图形,对称轴是它们的连心线.3.在图(1)中,两圆相外切,切点是A.因为切点A在连心线O1O2上,所以O1O2=O1A+O2A =R+r,即d=R+r:反之,当d=R+r时,说明圆心距等于两圆半径之和,O1、A、O2在一条直线上,所以⊙O1与⊙O2只有一个交点A,即⊙O1与⊙O2外切.在图(2)中,⊙O1与⊙O2相内切,切点是B.因为切点B在连心线O1O2,所以O1O2=O1B-O2B,即d=R-r:反之,当d=R-r时,圆心距等于两半径之差,即O1O2=O1B-O2B,说明O1、O2、B在一条直线上,B既在⊙O1上,又在⊙O2上,所以⊙O1与⊙O2内切.当两圆相外切时,有d=R+r,反过来,当d=R+r时,两圆相外切,即两圆相外切 d=R+r当两圆相内切时,有d=R-r,反过来,当d=R-r时,两圆相内切,即两圆相内切d =R-r.设两圆半径分别为R和r,圆心矩为d,那么(1)两圆外离d>R+r(2)两圆外切d=R+r(3)两圆相交R-r<d<R=r(R≥r)(4)两圆内切d=R-r(R>r)(5)两圆内含d<R-r(R>r)同心圆d=04.定理:相交两圆的连心线垂直平分两圆的公共弦.1.两个同样大小的肥皂泡黏(点O,O′是圆心),分隔两个肥皂泡的肥皂膜PQ成一条直线,TP、NP分别为两圆的切线,求∠TPN的大小.分析:因为两个圆大小相同,所以半径OP=O′P=OO′,又TP、NP分别为两圆的切线,所以PT⊥OP,PN⊥O′P,即∠OPT=∠O′PN=90°,所以∠TPN等于360°减去∠OPT+∠O′PN+∠OPO°即可.【解析】∵OP =OO′=PO′,∴△PO′O是一个等边三角形.∴∠OPO′=60°.又∵TP与NP分别为两圆的切线,∴∠TPO=∠NPO′=90°.∴∠TPN=360°-2× 90°-60°=120°.2.如图⊙O的半径为5cm,点P是⊙O外一点,OP=8cm.求:(1)以P为圆心作⊙P与⊙O外切,小圆⊙P的半径是多少?(2)以P为圆心作⊙P与⊙O内切,大圆⊙P的半径是多少?【解析】(1)设⊙O与⊙P外切于点A.∴ PA=OP-OA=8-5,∴ PA=3cm.(2)设⊙O与⊙p内切于点B.∴ PB=OP+OB=8+5,∴ PB=13cm.(3)如图7-101,⊙O2与以O1为圆心的同心圆相交于A、B、C、D.3.求证:四边形ABCD是等腰梯形.分析:欲证明四边形ABCD是等腰梯形,只需证明AB∥CD,AD=BC且AB≠CD即可.【解析】证明:连结O1O2,∵⊙O2与以O1为圆心的圆相交于A、B、C、D,∴ AB⊥O1O2,DC⊥O1O2.∴ AB∥CD.在⊙O2中,∵AB∥CD,又∵ AB≠CD,∴四边形ABCD是等腰梯形.4.已知:如图7-102,A是⊙O1、⊙O2的一个交点,点P是O1O2的中点.如果过A的直线MN垂直于PA,交⊙O1于M,交⊙O2于N.那么AM与AN有什么关系呢?是O1O2中点,由平行线等分线段定理可得AC=AD,而得结论.【解析】证明:过点O1、O2分别作O1C⊥MN,O2D⊥MN,垂足为C、D,又∵ PA⊥MN,∴ PA∥O1C∥O2D,∵O1P=O2P,∴ AC=AD.∴ AM=AN.。
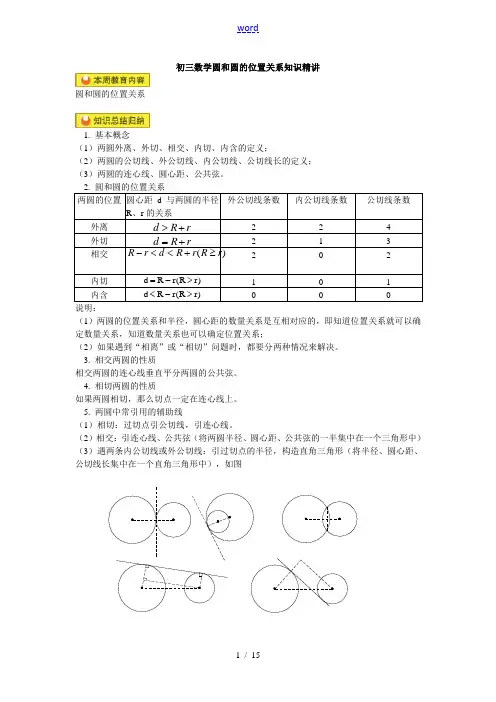
初三数学圆和圆的位置关系知识精讲圆和圆的位置关系1. 基本概念(1)两圆外离、外切、相交、内切、内含的定义;(2)两圆的公切线、外公切线、内公切线、公切线长的定义; (3)两圆的连心线、圆心距、公共弦。
两圆的位置 圆心距d 与两圆的半径R 、r 的关系 外公切线条数内公切线条数公切线条数外离 d R r >+ 2 2 4 外切 d R r =+2 13 相交 R r d R r R r -<<+≥()2 0 2 内切 d R r R r =->()1 0 1 内含d R r R r <->()说明:(1)两圆的位置关系和半径,圆心距的数量关系是互相对应的,即知道位置关系就可以确定数量关系,知道数量关系也可以确定位置关系;(2)如果遇到“相离”或“相切”问题时,都要分两种情况来解决。
3. 相交两圆的性质相交两圆的连心线垂直平分两圆的公共弦。
4. 相切两圆的性质如果两圆相切,那么切点一定在连心线上。
5. 两圆中常引用的辅助线(1)相切:过切点引公切线,引连心线。
(2)相交:引连心线、公共弦(将两圆半径、圆心距、公共弦的一半集中在一个三角形中) (3)遇两条内公切线或外公切线:引过切点的半径,构造直角三角形(将半径、圆心距、例:(1997某某)如图,已知:两圆内切于点A,P是两圆公切线上的一点过P作小圆的割线PBC,连结AB、AC,并延长分别交大圆于D、E,求证:PCPBAEAD=22。
证明:连结DEPA是两圆的公切线,∴∠=∠=∠PAD PCA E∴∴=BC DEAEADACAB//PA是⊙O1的切线,PBC是⊙O1的割线∴=⋅PA PB PC2又 ∠=∠∠=∠PCA PAB CPA APB,∴∴=∆∆PAB PCAACABPCPA~∴=∴==⋅=AEADPCPAAEADPCPAPCPB PCPCPB22222即PCPBAEAD=22说明:相切两圆中公切线是联系两圆中角的最有利条件,利用两圆的公切线,构造两圆的弦切角来进行角的转化。

1、了解圆与圆的五种位置关系;2、经历探索两圆的位置关系与两圆半径、圆心距的数量关系间的内在联系的过程,并运用相关结论解决问题; 第一课时 圆与圆的位置关系知识点梳理1、⊙O 的半径是6,圆心到直线l 的距离为3,则直线l 与⊙O 的位置关系是( )A .相交B .相切C .相离D .无法确定2、如图1,AB 与⊙O 切于点B ,AO =6㎝,AB =4㎝,则⊙O 的半径为( )A 、45㎝B 、25㎝C 、213㎝D 、13㎝3、如图2,已知⊙0的直径AB 与弦AC 的夹角为35°,过C 点的切线PC 与AB 的 延长线交于点P ,则么∠P 等于( )A .150B .200C .250D .300图1 图2 图34、如图3,AB 与⊙O 切于点C ,OA=OB ,若⊙O 的直径为8cm ,AB=10cm ,那么OA 的长是( ) A .41 B .40.14.60C D5、已知:如图,△ABC 中,AC =BC ,以BC 为直径的⊙O 交AB 于点D ,过点D 作DE ⊥AC 于点E ,交BC 的延长线于点F . 求证:(1)AD =BD ; (2)DF 是⊙O 的切线.课前检测FEDCBAOB A CO(一)两圆位置关系的定义 注:(1)找到分类的标准:①公共点的个数;②一个圆上的点是在另一个圆的内部还是外部(2)两圆相切是指两圆外切与内切 (3)两圆同心是内含的一种特殊情况(二)两圆位置关系与两圆半径、圆心距的数量关系之间的联系:两圆的半径分别为R 、r ,圆心距为d ,那么两圆外离d > R +r 两圆外切d = R +r两圆相交R -r < d <R +r (R ≥r ) 两圆内切 d = R -r (R > r ) 两圆内含d < R -r (R > r )(三).借助数轴进一步理解两圆位置关系与量关系之间的联系知识梳理O 1O 2O 1O 2O 1O 2O 1O 2O 1O 2⇔⇔第二课时 圆与圆的位置关系典型例题一、圆与圆位置关系的确定例1.右图是北京奥运会自行车比赛项目标志,图中两车轮所在圆的位置关系( )A .内含B .相交C .相切D .外离变1.如图是一个五环图案,它由五个圆组成.下排的两个圆的位置关系是( )A .内含B .外切C .相交D .外离例2.右图是一个“众志成城,奉献爱心”的图标,图标中两圆的位置关系是A .外离B .相交C .外切D .内切变2.如图,日食图中表示太阳和月亮的分别为两个圆,这两个圆的位置关系是.例3.图中圆与圆之间不同的位置关系有( )A .2种B .3种C .4种D .5种变3.(1)大圆半径为6,小圆半径为3,两圆圆心距为10,则这两圆的位置关系为( )A .外离B .外切 C.相交 D .内含(2)已知⊙O 1的半径r 为3cm ,⊙O 2的半径R 为4cm ,两圆的圆心距O 1O 2为1cm ,则这两圆的位置关系是( )A .相交B .内含C .内切D .外切 (3)已知1O ⊙与2O ⊙的半径分别为5cm 和3cm ,圆心距127cm O O ,则两圆的位置关系是( )A .外离B .外切C .相交D .内切典型例题O 3O 2O 1例4.如图,点A B ,在直线MN 上,11AB =厘米,A B ,的半径均为1厘米.A 以每秒2厘米的速度自左向右运动,与此同时,B 的半径也不断增大,其半径r (厘米)与时间t (秒)之间的关系式为1r t =+(0)t ≥.(1)试写出点A B ,之间的距离d (厘米)与时间t (秒)之间的函数表达式; (2)问点A 出发后多少秒两圆相切?变4.如图,A B 、⊙⊙的圆心A B ,在直线l 上,两圆半径都为1cm ,开始时圆心距4cm AB =,现A B ⊙⊙,同时沿直线l 以每秒2cm 的速度相向移动,则当两圆相切时,A ⊙运动的时间为秒.二、圆与圆位置关系的性质例5.已知1O 和2O 外切,它们的半径分别为2cm 和5cm ,则12O O 的长是( )A .2cmB .3cmC .5cmD .7cm变5.O 的半径为3cm ,点M 是O 外一点,4OM cm =,则以M 为圆心且与⊙O 相切的圆的半径是cm .例6.1O ⊙和2O ⊙相切,1O ⊙的直径为9cm ,2O ⊙的直径为4cm .则12O O 的长是_________.变6.如图,1O ,2O ,3O 两两相外切,1O 的半径11r =,2O 的半径22r =,3O 的半径33r =,则123O O O △是( )A .锐角三角形B .直角三角形C .钝角三角形D .锐角三角形或钝角三角形例7.若A ⊙和B ⊙相切,它们的半径分别为8cm 和2cm ,则圆心距AB 为_______________.NMB A PO 2O 1BA l。
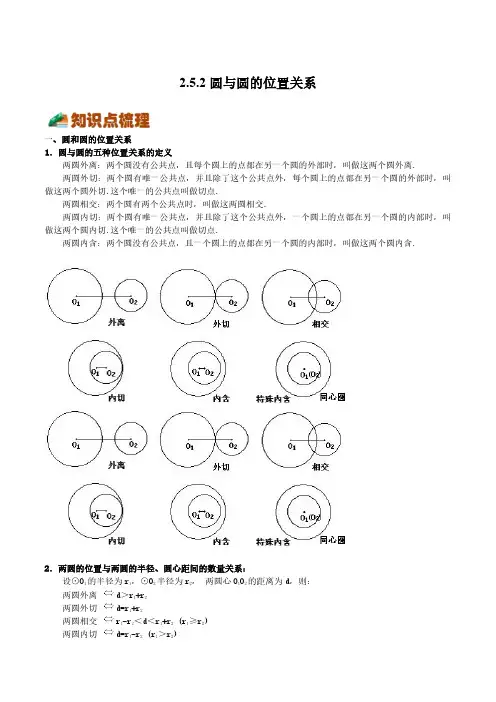
2.5.2圆与圆的位置关系一、圆和圆的位置关系1.圆与圆的五种位置关系的定义 两圆外离:两个圆没有公共点,且每个圆上的点都在另一个圆的外部时,叫做这两个圆外离. 两圆外切:两个圆有唯一公共点,并且除了这个公共点外,每个圆上的点都在另一个圆的外部时,叫做这两个圆外切.这个唯一的公共点叫做切点. 两圆相交:两个圆有两个公共点时,叫做这两圆相交. 两圆内切:两个圆有唯一公共点,并且除了这个公共点外,一个圆上的点都在另一个圆的内部时,叫做这两个圆内切.这个唯一的公共点叫做切点. 两圆内含:两个圆没有公共点,且一个圆上的点都在另一个圆的内部时,叫做这两个圆内含.2.两圆的位置与两圆的半径、圆心距间的数量关系: 设⊙O1的半径为r1,⊙O2半径为r2,两圆心O1O2的距离为d,则: 两圆外离d>r1+r2 两圆外切d=r1+r2 两圆相交r1-r2<d<r1+r2(r1≥r2) 两圆内切d=r1-r2(r1>r2) 两圆内含d<r1-r2(r1>r2)要点: (1) 圆与圆的位置关系,既考虑它们公共点的个数,又注意到位置的不同,若以两圆的公共点个数分类,又可以分为:相离(含外离、内含)、相切(含内切、外切)、相交; (2) 内切、外切统称为相切,唯一的公共点叫作切点; (3) 具有内切或内含关系的两个圆的半径不可能相等,否则两圆重合.A .2种B .3种C .4种D .5种【答案】A 【解析】由图形可以看出,有两种位置关系,相交和内切.故选A.题型2:根据圆与圆的位置关系求半径4.已知1O e 与2O e 相切,若1O e 的半径为3cm ,127cm O O =,,则2O e 的半径为( )A .4cm 或12cmB .10cm 或6cmC .4cm 或10cmD .6cm 或12cm【答案】C【分析】根据圆与圆的位置关系,内切时()2121d r r r r =->,外切时12d r r =+,计算即可.【解析】解:两圆内切时,2O e 的半径7310=+=(cm),外切时,2O e 的半径734=-=(cm),∴2O e 的半径为4cm 或10cm .故选:C .【点睛】本题考查了圆与圆的位置关系,熟练掌握知识点是解题的关键.5.如果两圆有两个交点,且圆心距为13,那么此两圆的半径可能为( )A .1、10B .5、8C .25、40D .20、30【答案】D【分析】先由两圆有两个交点得到两圆相交,然后根据半径与圆心距之间的关系求解即可.【解析】∵两圆有两个交点,∴两圆相交,∵圆心距为13∴两圆的半径之差小于13,半径之和大于13.A .1101113+=<,故不符合题意;B .5813+=,故不符合题意;【点睛】此题重点考查圆与圆的位置关系、线段的垂直平分线的性质、勾股定理以及数形结合与分类讨论数学思想的运用等知识与方法,正确地作出所需要的辅助线是解题的关键.9.已知两圆的半径分别为2和5,如果这两圆内含,那么圆心距A.0<d<3B.0<d<7C.3<d<7A.45°B.30°【答案】B【分析】连接O1O2,AO2,O1B,可得【解析】解:连接O1O2,AO2,O∵O 1B = O 1A∴112112O AB O BA AO O Ð=Ð=Ð ∵⊙O 1和⊙O 2是等圆,∴AO 1=O 1O 2=AO 2,∴△AO O 是等边三角形,【点睛】本题考查了相交两圆的性质以及等边三角形的判定与性质,得出21AO O D 是等边三角形是解题的关键.题型5:分类讨论13.已知圆1O 、圆2O 的半径不相等,圆1O 的半径长为5,若圆2O 上的点A 满足15AO =,则圆1O 与圆2O 的位置关系是( )A .相交或相切B .相切或相离C .相交或内含D .相切或内含【答案】A【分析】根据圆与圆的位置关系,分类讨论.【解析】解:如图所示:当两圆外切时,切点A 能满足15AO =,当两圆相交时,交点A 能满足15AO =,当两圆内切时,切点A 能满足15AO =,当两圆相离时,圆2O 上的点A 不能满足15AO =,所以,两圆相交或相切,故选:A .【点睛】本题考查了由数量关系来判断两圆位置关系的方法.14.如图,长方形ABCD 中,4AB =,2AD =,圆B 半径为1,圆A 与圆B 外切,则点C 、D 与圆A 的位置关系是( )A .点C 在圆A 外,点D 在圆C .点C 在圆A 上,点D 在圆【答案】A 【分析】先根据两圆外切求出圆A 的半径,连接【解析】解:∵4AB =,圆B 半径为【点睛】本题考查了点与圆的位置关系、圆与圆的位置关系、勾股定理,熟练掌握点与圆的位置关系是关键,还利用了数形结合的思想,通过图形确定圆的位置.15.如图,1O e ,2O e 的圆心 1O ,128cm O O =.1O e 以 1cm /s 的速度沿直线A .外切B .相交C .内切D .内含【答案】D 【分析】先求出7s 后,两圆的圆心距为1cm ,结合两圆的半径差即可得到答案.【解析】解:∵1O e 的半径为 2cm ,2O e 的半径为 3cm ,128cm O O =.1O e 以 1cm /s 的速度沿直线 l 向右运动,7s 后停止运动.∴7s 后,两圆的圆心距为1cm ,此时两圆的半径差为321cm -=,∴此时两圆内切,∴在此过程中,1O e 与 2O e 没有出现的位置关系是:内含,故选D .【点睛】本题主要考查圆与圆的位置关系,掌握d R r =+,则两圆外切,d R r =-,则两圆外切,是关键.题型6:圆的位置关系综合16.如图,∠MON =30°,p 是∠MON 的角平分线,PQ 平行ON 交OM 于点Q ,以P 为圆心半径为4的圆ON 相切,如果以Q 为圆心半径为r 的圆与P Q 相交,那么r 的取值范围是( )A .4<r <12B .2<r <12C .4<r <8D .r >4【答案】A 【分析】过点Q 作QA ⊥AN 于A ,过点P 作PB ⊥ON 于B ,得到四边形ABPQ 是矩形,QA=PB=4,根据∠MON =30°求出OQ=2QA=8,根据平行线的性质及角平分线的性质得到PQ=8,再分内切与外切两种求出半径r ,即可得到两圆相交时的半径r 的取值范围.【解析】过点Q 作QA ⊥AN 于A ,过点P 作PB ⊥ON 于B ,∵PQ ∥ON ,∴PQ ⊥PB ,∴∠QAB=∠QPB=∠PBA=90°,∴四边形ABPQ 是矩形,∴QA=PB=4,∵∠MON =30°,∴OQ=2QA=8,∵OP 平分∠MON ,PQ ∥ON ,∴∠QOP=∠PON=∠QPO ,∴PQ=OQ=8,当以Q 为圆心半径为r 的圆与P Q 相外切时,r=8-4=4,当以Q 为圆心半径为r 的圆与P Q 相内切时,r=8+4=12,∴以Q 为圆心半径为r 的圆与P Q 相交,4<r<12,故选:A.【点睛】此题考查角平分线的性质,平行线的性质,矩形的判定及性质,两圆相切的性质.17.如图,在Rt ABC V 中,90C Ð=°,4AC =,7BC =,点D 在边BC 上,3CD =,A e 的半径长为3,D e 与A e 相交,且点B 在D e 外,那么D e 的半径长r 可能是( )A .1r =B .3r =C .=5r D .7r =【答案】B 【分析】连接AD 交A e 于E ,根据勾股定理求出AD 的长,从而求出DE DB 、的长,再根据相交两圆的位置关系得出r 的范围即可.【解析】解:连接AD 交A e 于E ,如图1,在Rt ACD V 中,由勾股定理得:则532DE AD AE =-=-=,73BC CD ==Q ,,734BD \=-=,\D e A eA .142r <<B .52r <<【答案】C【分析】过点O 作OE AD ^,勾股定理求得11,OE AB OF AD ==,根据题意,画出相应的图形,即可求解.当圆O 与CD 相切时,过点O 作OF CD ^于点F ,如图所示,则162OF AD ==则1325622r =+=∴O e 与直线AD 相交、与直线CD 相离,且D e 与O e 内切时,作AD⊥BC,以A为圆心,以AD为半径画圆一、单选题1.如果两圆的半径长分别为5和3,圆心距为8,那么这两个圆的位置关系是()A.内切B.外离C.相交D.外切【答案】D【分析】根据两圆半径的和与圆心距,即可确定两圆位置关系.【解析】解:∵两圆的半径长分别为5和3,圆心距为8,538+=,∴两圆外切,故选:D .【点睛】本题考查了圆与圆的位置关系,解题的关键是掌握:外离,则d R r >+;外切,则d R r =+;相交,则R r d R r -<<+;内切,则d R r =-;内含,则d R r <-.2.两圆的半径分别为2和3,圆心距为7,则这两个圆的位置关系为( )A .外离B .外切C .相交D .内切【答案】A【分析】本题直接告诉了两圆的半径及圆心距,根据它们数量关系与两圆位置关系的对应情况便可直接得出答案.【解析】解:∵两圆的半径分别为2和3,圆心距为7,又∵7>3+2,∴两圆的位置关系是:外离.故选A .【点睛】本题主要考查了圆与圆的位置关系,解题的关键在于能够准确掌握相关知识进行求解.3.已知直径分别为6和10的两圆没有公共点,那么这两个圆的圆心距的取值范围是( )A .d >2B .d >8C .d >8或0≤d <2D .2≤d <8【答案】C【分析】分两种情况讨论:当两圆外离时,两圆没有公共点时,当两圆内含时,两圆没有公共点时,从而可得答案.【解析】解:Q 直径分别为6和10的两圆没有公共点,\ 两圆的半径分别为3和5,当两圆外离时,两圆没有公共点时,8,d >当两圆内含时,两圆没有公共点时,02,d £<综上:所以两圆没有公共点时,8d >或0 2.d £<故选C【点睛】本题考查的是两圆的位置关系,熟练的运用两圆外离与内含的定义解题是解本题的关键.4.已知点()4,0A ,()0,3B ,如果⊙A 的半径为2,⊙B 的半径为7,那么⊙A 与⊙B 的位置关系( )【点睛】本题考查了两圆外切的条件,两圆相交的条件,等腰直角三角形的性质和对称性,熟练掌握两圆D .当⊙1O 与⊙2O 没有公共点时,1202O O <≤.【答案】D【分析】根据圆与圆位置关系的性质,对各个选项逐个分析,即可得到答案.【解析】当1224O O <<时,⊙1O 与⊙2O 相交,有两个公共点,故选项A 描述正确;当⊙1O 与⊙2O 有两个公共点时,1224O O <<,故选项B 描述正确;当1202O O <≤时,⊙1O 与⊙2O 没有公共点,故选项C 描述正确;当⊙1O 与⊙2O 没有公共点时,1202O O <≤或124O O >,故选项D 描述错误;故选:D .【点睛】本题考查了圆与圆位置关系的知识;解题的关键是熟练掌握圆与圆位置关系的性质,从而完成求解.9.如图,矩形ABCD 中,AB=4,BC=6,以A 、D 为圆心,半径分别为2和1画圆,E 、F 分别是⊙A 、⊙D 上的一动点,P 是BC 上的一动点,则PE+PF 的最小值是( )A .5B .6C .7D .8【答案】C 【分析】以BC 为轴作矩形ABCD 的对称图形A′BCD′以及对称圆D′,连接AD′交BC 于P ,交⊙A 、⊙D′于E 、F′,连接PD ,交⊙D 于F ,EF′就是PE+PF 最小值;根据勾股定理求得AD′的长,即可求得PE+PF 最小值.【解析】解:如图,以BC 为轴作矩形ABCD 的对称图形A′BCD′以及对称圆D′,连接AD’交BC 于P ,则EF′就是PE+PF最小值;∵矩形ABCD中,AB=4,BC=6,圆A的半径为2,圆D的半径为1,∴A′D′=BC=6,AA′=2AB=8,AE=2,D′F′=DF=1,∴AD′=10,EF′=10-2-1=7∴PE+PF=PF′+PE=EF′=7,故选C.【点睛】本题考查了轴对称-最短路线问题,勾股定理的应用等,作出对称图形是解答本题的关键.10.如图,在⊙O中,弦AD等于半径,B为优弧AD上的一动点,等腰△ABC的底边BC所在直线经过点D.若⊙O的半径等于1,则OC的长不可能为()A.2﹣B.﹣1C.2D.+1【答案】A【解析】试题分析:利用圆周角定理确定点C的运动轨迹,进而利用点与圆的位置关系求得OC长度的取值范围.解:如图,连接OA、OD,则△OAD为等边三角形,边长为半径1.作点O关于AD的对称点O′,连接O′A、O′D,则△O′AD也是等边三角形,边长为半径1,∴OO′=×2=.由题意可知,∠ACB=∠ABC=∠AOD=30°,∴∠ACB=∠AO′D,∴点C在半径为1的⊙O′上运动.由图可知,OC长度的取值范围是:﹣1≤OC≤+1.故选A.考点:相交两圆的性质;轴对称的性质.二、填空题当1O e 位于2O e 外部,且P ,1O ,2O 位于同一条直线上时,如图所示,min 121523r O O PO =-=-=.故答案为:37r ££.【点睛】本题主要考查圆与圆的位置关系,能采用数形结合的方法和分类讨论的思想分析问题是解题的关键.16.在矩形ABCD 中,5AB =,8AD =,点E 在边AD 上,3AE =图),点F 在边BC 上,以点F 为圆心、CF 为半径作F e .如果F e【答案】4116【分析】连接EF ,作FH 股定理得到()(235r r +=-【解析】解:连接EF ,作BQe过点A,且7AB=,由函数图象可知,当即不等式①的解集为同理可得:不等式②【点睛】此题主要考查了相交两圆的性质以及勾股定理,熟练利用正三角形以及正方形的性质是解题关键.20.已知A e ,B e ,C e 【答案】A e 的半径为2厘米,(1)设AP =x ,求两个圆的面积之和S ;(2)当AP 分别为13a 和12a 时,比较S 【答案】(1)22111422a ax x p p p -+11求:(1)弦AC的长度;(2)四边形ACO1O2的面积.【答案】(1)8(2)21(2)解:在2Rt AO E △中,由勾股定理得:∴1212426O O O E O E =+=+=∴1111831222O AC S AC O D ==´´=g △,S ∴四边形ACO 1O 2的面积为:S S +(1)如图1所示,已知,点()02A ,,点()32B ,.①在点()()()123011141P P P -,,,,,中,是线段AB 的“对称平衡点”的是___________②线段AB 上是否存在线段AB 的“对称平衡点”?若存在,请求出符合要求的 “对称平衡点若不存在,请说明理由;(2)如图2,以点()02A ,为圆心,1为半径作A e .坐标系内的点C 满足2AC =,再以点作C e ,若C e 上存在A e 的“对称平衡点”,直接写出C 点纵坐标C y 的取值范围.【答案】(1)①1P ,3P ;②不存在,理由见解析(2)02c y ££∴线段AB的“对称平衡点”的是1P,故答案为:1P,3P;②不存在设P为线段AB上任意一点,则它与线段££,PA PB33点P关于x轴的对称点为P¢,它到线段,是线段AB上的任意两点,即若M N∵()()0,2,0,0A O ∴02c y ££【点睛】本题考查了对称平衡点.两圆的位置关系,点与圆的位置关系等知识,解题的关键是理解题意,学会取特殊点特殊位置解决问题.。



九年级数学圆与圆的位置关系在我们学习数学的过程中,有些知识总是能让人拍案叫绝,比如说圆与圆之间的位置关系。
你想啊,两个圆就像两个好朋友,有时候紧紧相拥,有时候则是形同陌路。
今天咱们就来聊聊这些圆的“社交”动态,保准让你听了哈哈大笑,边学边乐。
首先呢,咱们得知道圆和圆之间的基本关系。
两个圆如果能够相交,形成两个交点,那就叫做“相交”。
这就好比是两位朋友在某个聚会上聊得火热,结果发现两个人的兴趣爱好还真是有那么一点点相似,嘿嘿,意外的发现吧。
如果这两个圆的距离刚刚好,让它们只轻轻碰了一下,那就叫做“相切”。
就像两个朋友在街上偶遇,点头致意一下,心照不宣,继续各自的旅程,既亲密又有些距离。
哦,对了,记得咱们的圆心距离和半径的关系。
圆心距小于半径之和,那就能相交;等于半径之和,那就相切;大于半径之和,嘿,那就各自飞了。
咱们得聊聊“相离”这种情况。
两圆如果完全不相交,远得像两个恋人各自生活在两个城市,联系得少之又少,那就是“相离”。
你想啊,两个圆心的距离大于半径之和,真是远得像是天涯海角,不同的生活方式,不同的爱好,没啥交集,生活就这么各自精彩。
想象一下,两个圆在画纸上悄悄地待着,互不干扰,彼此就是那种“风马牛不相及”的感觉。
再来看看特殊的情况。
比如,当两个圆的圆心重合,但半径不同,那就有点意思了。
想象一下,有个圆在外面转来转去,另一个圆在它的“肚子”里悄悄待着。
这个时候,内圆完全被外圆包裹住了,像极了朋友间的包容。
总有那么一个人,给你无条件的支持,虽然不总是被看到,但心里永远有那么一个位置。
可惜,这种情况可不是每个人都能理解的。
说到这里,咱们再来琢磨一下这些圆之间的关系的意义。
生活中,朋友之间的关系也好,爱人之间的互动也罢,都是那么复杂又简单。
有人总是希望彼此相交,有人则想要独立。
相交的朋友就像是在一起打游戏,总是能碰撞出各种火花,而相切的朋友则是在适当的时候给予彼此空间,既能相互支持,又能保留个人的独特性。
圆和圆的位置关系(圆和圆的相离,圆与圆的相交,圆与圆的相切)◎圆和圆的位置关系(圆和圆的相离,圆与圆的相交,圆与圆的相切)的定义圆和圆的位置关系:如果两个圆没有公共点,那么就说这两个圆相离,相离分为外离和内含两种。
如果两个圆只有一个公共点,那么就说这两个圆相切,相切分为外切和内切两种。
如果两个圆有两个公共点,那么就说这两个圆相交。
圆心距:两圆圆心的距离叫做两圆的圆心距。
◎圆和圆的位置关系(圆和圆的相离,圆与圆的相交,圆与圆的相切)的知识扩展1、圆和圆的位置关系:如果两个圆没有公共点,那么就说这两个圆相离,相离分为外离和内含两种。
如果两个圆只有一个公共点,那么就说这两个圆相切,相切分为外切和内切两种。
如果两个圆有两个公共点,那么就说这两个圆相交。
2、圆心距:两圆圆心的距离叫做两圆的圆心距。
3、圆和圆位置关系的性质与判定:设两圆的半径分别为R和r,圆心距为d,那么两圆外离d>R+r两圆外切d=R+r两圆相交R-r<d<R+r(R≥r)两圆内切d=R-r(R>r)两圆内含d<R-r(R>r)4、两圆相切的性质:(1)连心线:两圆圆心的连线。
(2)两圆相切的性质:相切两圆的连心线必过切点,即两圆圆心、切点三点在一条直线上。
◎圆和圆的位置关系(圆和圆的相离,圆与圆的相交,圆与圆的相切)的特性圆和圆位置关系的性质与判定:设两圆的半径分别为R和r,圆心距为d,那么两圆外离d>R+r(没有交点)两圆外切d=R+r (有一个交点,叫切点)两圆相交R-r<d<R+r(R≥r)(有两个交点)两圆内切d=R-r(R>r) (有一个交点,叫切点)两圆内含d<R-r(R>r)(没有交点)两圆相切的性质:(1)连心线:两圆圆心的连线。
(2)两圆相切的性质:相切两圆的连心线必过切点,即两圆圆心、切点三点在一条直线上。
◎圆和圆的位置关系(圆和圆的相离,圆与圆的相交,圆与圆的相切)的教学目标1、掌握圆和圆的五种位置关系的定义、性质及判定方法并能解决简单的问题。
初中数学知识归纳圆与圆之间的位置关系圆与圆之间的位置关系是初中数学中的一个重要内容,它涉及到圆的相交关系、包含关系以及外切关系等多个方面。
通过归纳总结,我们可以更好地理解和运用这些知识点。
一、相离关系当两个圆没有任何交点时,它们被称为相离的圆。
两个相离的圆之间的最大距离等于它们的半径之和。
二、外切关系如果两个圆的半径相等,并且它们的圆心之间的距离等于两个圆的半径之和,我们称这两个圆为外切的圆。
三、相交关系相交是指两个圆的内部空间存在公共点。
根据两个圆的圆心之间的距离和半径的关系,相交的情况又可以分为四种。
1.相交于两点当两个圆的圆心之间的距离小于两个圆的半径之和,并且大于两个圆的半径之差时,两个圆相交于两个点。
2.相切于外点当两个圆的圆心之间的距离等于两个圆的半径之和时,两个圆相切于外点。
3.相切于内点当两个圆的圆心之间的距离等于两个圆的半径之差时,两个圆相切于内点。
4.相切于公切线当两个圆的圆心之间的距离等于两个圆的半径之和,并且两个圆的半径不相等时,两个圆相切于一条公切线。
四、内含关系如果一个圆的内部完全位于另一个圆内部,我们称这两个圆为内含的关系。
在内含的情况下,内含圆的半径小于包含圆的半径。
五、包含关系如果一个圆的外部完全包含另一个圆,我们称这两个圆为包含的关系。
在包含的情况下,包含圆的半径大于内含圆的半径。
通过对圆与圆之间的位置关系进行归纳整理,我们可以更好地理解和应用这些知识点。
在解决相关题目时,我们可以根据题目给出的条件和要求,运用这些位置关系进行分析和推理。
同时,我们还可以通过观察图形特点和运用相关定理来判断两个圆之间的位置关系,从而解决问题。
初中数学中的圆与圆之间的位置关系是一个基础而重要的内容,它不仅在几何学中有广泛的应用,而且在实际生活和工程中也有着重要的作用。
通过掌握和运用这些知识,我们可以更好地理解和应用数学,为解决实际问题提供有力的支持。
第八讲 圆(三)——圆和圆的位置关系1、定义:(1)如果两个圆没有公共点,那么就说这两个圆相离。
外离:两个圆没有公共点,并且每个圆上的点都在另一个圆的外部时,叫做这两个圆外离。
(图(1))内含:两个圆没有公共点,并且一个圆上的点都在另一个圆的内部时,叫做这两个圆内含(图(5))。
两圆同心是两圆内含的一个特例。
(图(6))(2)如果两个圆只有一个公共点,那么就说这两个圆相切外切:两个圆有唯一的公共点,并且除了这个公共点以外,每个圆上的点都在另一个圆的外部时,叫做这两个圆外切。
这个唯一的公共点叫做切点。
(图(2))内切:两个圆有唯一的公共点,并且除了这个公共点以外,一个圆上的点都在另一个圆的内部时,叫做这两个圆内切。
这个唯一的公共点叫做切点。
(图(4))(3)两个圆有两个公共点,此时叫做这两个圆相交。
(图(3)) 注意:(1)两圆外离与内含时,两圆都无公共点,但同时要考虑内部和外部的因素。
两圆外切与内切也有这样的比较。
(2)两圆外切和内切统称两圆相切,即外切和内切的共性是公共点的个数唯一。
(3)两圆位置关系的五种情况也可归纳为三类:相离(外离和内含);相交;相切(外切和内切)。
2. 两圆位置关系的性质:;-r-r <d <R+r ; >R+r <R -r为了方便记忆,将这五种数量关系用数轴表示为:补充:1.如果两个圆相切,那么切点一定在连心线上。
(轴对称来说明,证明可用反证法,不作要求) 2. 相交两圆的连心线垂直平分两圆的公共弦。
在解决有关相交两圆的问题时,常常添加以下几种辅助线:连心线、公共弦、连结交点与圆心。
从而可以把两圆半径、公共弦长的一半、圆心距集中到同一个三角形中,利用三角形的有关知识加以解决。
例题讲解1. (2011江苏南京,26,8分)如图,在Rt△ABC中,∠ACB=90°,AC=6㎝,BC=8㎝,P为BC的中点.动点Q从点P出发,沿射线PC方向以2㎝/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.⑴当t=1.2时,判断直线AB与⊙P的位置关系,并说明理由;⑵已知⊙O为△ABC的外接圆,若⊙P与⊙O相切,求t的值.2. (2011湖北黄石,24,9分)已知⊙O1与⊙O2相交于A、B两点,点O1在⊙O2上,C为O2上一点(不与A,B,O1重合),直线CB与⊙O1交于另一点D。
教学目标
重点、难点考点及考试要求1、了解圆与圆的五种位置关系;
2、经历探索两圆的位置关系与两圆半径、圆心距的数量关系间的内在联系的过程,并运用相关结论解决问题;
1、位置关系与对应数量关系的运用
2、两圆的位置关系对应数量关系的探索
1、圆与圆的五种位置关系
2、两圆的位置关系与两圆半径、圆心距的数量关系
教学内容
第一课时圆与圆的位置关系知识点梳理
课前检测
1、⊙ O的半径是 6,圆心到直线l的距离为 3,则直线l与⊙ O的位置关系是()
A.相交B.相切C.相离D.无法确定
2、如图 1,AB与⊙ O切于点 B, AO=6 ㎝, AB= 4 ㎝,则⊙ O的半径为()
A、4 5 ㎝
B、25 ㎝
C、2 13㎝
D、13 ㎝
3、如图 2,已知⊙ 0 的直径 AB与弦 AC的夹角为 35°,过 C点的切线 PC与 AB的
延长线交于点 P,则么∠ P 等于()
A.150B.200C.250D.300
图 1图2图3
4、如图 3,AB与⊙ O切于点 C, OA=OB,若⊙ O的直径为 8cm,AB=10cm,那么 OA的长是()
A.41B.40 C. 14 D. 60
5、已知:如图,△ ABC中, AC=BC,以 BC为直径的⊙ O交 AB于点
D,过点 D 作 DE⊥ AC于点 E,交 BC的延长线于点 F.
求证:( 1) AD=BD;(2)DF是⊙ O的切线.
知识梳理
(一)两圆位置关系的定义
注:( 1)找到分类的标准:
①公共点的个数;
②一个圆上的点是在另一个圆的内部还是外部
(2)两圆相切是指两圆外切与内切
(3)两圆同心是内含的一种特殊情况
(二)两圆位置关系与两圆半径、圆心距的数量关系之间的联系:两圆的半径分别为R、r ,圆心距为 d,那么
两圆外离 d > R+r
两圆外切 d =R+r
两圆相交R- r< d < R+ r ( R≥ r )
两圆内切 d =R-r (R > r )
两圆内含 d < R-r (R > r )
(三) . 借助数轴进一步理解两圆位置关系与量关系之间的联系
第二课时圆与圆的位置关系典型例题典型例题
一、圆与圆位置关系的确定
例 1. 右图是北京奥运会自行车比赛项目标志,A.内含B.相交 C .相切
图中两车轮所在圆的位置关系
( D .外离
)
变 1.如图是一个五环图案,它由五个圆组成.下排的两个圆的位置关系是()A.内含B.外切C.相交D.外离
例 2.右图是一个“众志成城,奉献爱心”的图标,图标中两圆的位置关系是
A.外离B.相交
C.外切D.内切
变 2.如图,日食图中表示太阳和月亮的分别为两个圆,这两个圆的位置关系
是.
例 3.图中圆与圆之间不同的位置关系有()
A.2 种B.3 种C.4 种D. 5 种
变 3. ( 1)大圆半径
为A.外离6,小圆半径为 3,两圆圆心距为10,则这两圆的位置关系为()B.外切C.相交D.内含
(2)已知⊙ O1的半径r为 3cm,⊙ O2的半径 R 为 4cm,两圆的圆心距 O1O2为 1cm,则这两圆的位置关系是()
A.相交B.内含C.内切D.外切
( 3)已知⊙O1与⊙O2的半径分别为5cm和3cm,圆心距O1O27cm ,则两圆的位置关系是()A.外离B.外切C.相交D.内切
例 4. 如图,点A,B在直线MN上,AB11厘米,A B 的半径均为1厘米. A 以每秒2厘米的速度自左向右运动,与此同时, B 的半径也不断增大,其半径r (厘米)与时间t(秒)之间的关系式为r 1 t (t≥0).
(1)试写出点A,B之间的距离d ( 厘米 ) 与时间t ( 秒 ) 之间的函数表达式;
(2)问点A出发后多少秒两圆相切?
M A B N
变 4. 如图,的圆心
A ,
B 在直线
l
上,两圆半径都为
1cm
,开始时圆心距
AB 4cm
,现
⊙ A ,⊙ B
⊙ A 、⊙ B
同时沿直线 l 以每秒2cm 的速度相向移动,则当两圆相切时,⊙ A 运动的时间为秒.
O
1P O
2A B
l
二、圆与圆位置关系的性质
例 5. 已知O1和O
2外切,它们的半径分别为2cm
和
5cm,则O
1O2的长是()
A. 2cm B.3cm C.5cm D.7cm
变 5.O 的半径为 3 cm ,点M是O 外一点, OM 4 cm ,则以M为圆心且与⊙O相切的圆的半径是cm .
例 6. ⊙O1和⊙O2相切,⊙O1的直径为9cm,⊙O2的直径为4cm.则O1O2的长是 _________.
变 6.如图,O1, O2, O3两两相外切, O1的半径 r1 1 , O2的半径 r2 2 , O3的半径 r3 3 ,则△O1O2 O3是()O2
A.锐角三角形B.直角三角形O3
O1
C.钝角三角形D.锐角三角形或钝角三角形
例 7.若⊙ A 和⊙ B 相切,它们的半径分别为 8cm 和 2cm ,则圆心距AB为_______________.
变 7. 已知两圆半径分别为 2 和 3,圆心距为d,若两圆没有公共点,则下列结论正确的是( ) A.0 d 1B.d5C.0 d 1或 d 5D.0≤d 1 或 d5
例 8. 一条皮带安装在半径是 14和 4 的两只皮带轮上 ( 皮带紧绷且不相交 ) ,若皮带在两只轮子切点间的距离是 24,那么两轮圆心间的距离是 ___________.
变 8. ( 1)已知相切两圆的半径分别为 5cm 和 4cm ,这两个圆的圆心距是
OO 的取值范
( 2)已知⊙ O
和⊙ O 的半径分别为
1 和 ,如果两圆的位置关系为相交,那么圆心距
1 2
4 1 2
围在数轴上表示正确的是
.
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5
A
B
C
D
第三课时
圆与圆的位置关系课堂检测
课堂检测
1、⊙ O 和 ⊙O, 的半径分别是 3 ㎝和 4 ㎝,如果 OO =7 ㎝,则这两圆的位置关系是(
)
1
2
1 2
A .内含
B 相交
C 外切
D 外离
. .
.
、如图,平面直角坐标系中,⊙ O 半径长为
,点 P a
,0)
,⊙ P 的半径长为
,把⊙ P 向左平移,
2
1
(
2
当⊙ P 与⊙ O 相切时, a 的值为(
)
A .3
B .1
C .1,3
D .± 1,± 3
3、如图,⊙ M 与⊙ N 外切,MNl cm ,若⊙ M 的半径
为
cm ,则⊙ N 的半径为
cm 。
= 0
6
cm 的两个点 A 、B 在直线 l 上.它们分别以
2 cm s 和
1 cm s 的速度在 l 上同时向右
4、如图,相距 2
/ /
平移,当点 A ,B 分别平移到点 A 1,B 1 的位置时,半径为 1cm 的⊙ A 1,与半径为 BB 1 的⊙ B 相切.则
点 A 平移到点 A 1 ,所用的时间为 s .
5、已知:如图,三个半圆以此相外切,它们的圆心都在x 轴的正半轴上并与直线 y=3
x 相切,设
3
半圆 C1、半圆 C2、半圆 C3的半径分别是 r 1、r 2、 r 3,则当 r 1=1 时, r 3=
6、已知⊙O1与⊙O2的半径 r1、 r2分别是方程 x 26x8 0 的两实根,若⊙O1与⊙O2的圆心距d=
5.则⊙O1与⊙ O2的位置关系是 ___________.
、如图,以M(-
5,0)为圆心、
4
为半径的圆与 x 轴交于 A、B 两点, P 是⊙ M上异于 A、B 的一动
7
点,直线PA、PB分别交 y 轴
于C、D,以 CD为直径的⊙ N 与与 x 轴交于 E、F 两点,则 EF 的长()
A.等于
4 2B等于C等于
6
D 随 P 点位置的变化而变化. 4 3..
8、以数轴上的原点O为圆
心,
3
为半径的扇形中,圆心角∠ AOB°,另一个扇形是以点 P 为圆心,
=90
5 为半径,圆心角∠
CPD °,点 P 在数轴上表示实数 a,如图.如果两个扇形的圆弧部分(弧 AB =60
和弧 CD)相交,那么实数 a 的取值范围是.、如图,⊙O、⊙O相交于点 P、Q两点,其中
⊙O的半径 r ,⊙O的半径 r
=2 ,过点Q作CD⊥PQ
9=2,,分别交⊙ O和⊙ O于点 C、D,连结 CP、 DP,过点 Q任作一直线 A 交⊙ O和⊙ O于 A、B,连结AP、
BP、AC、 DB,且 AC与 DB的延长线交于点
E,
()求证:PA
2;()若PQ ,试求∠ E度数。
12=2
PB
10、如图,在 Rt△ABC中,∠ ACB=90°, AC=6cm,BC=8cm. P 为 BC的中点,动点 Q从点 P 出发,沿
射线 PC方向以 2cm/ s 的速度运动,以 P 为圆心, PQ长为半径作圆.设点Q运动的时间为t s.(1)当 t =1.2 时,判断直线 AB与⊙ P 的位置关系,并说明理由;
(2)已知⊙ O为△ ABC的外接圆.若⊙ P 与⊙ O相切,求 t 的值.。