当前位置：文档之家 › 晶体结构的对称性

晶体结构的对称性

  • 格式：doc
  • 大小：47.50 KB
  • 文档页数：4

下载文档原格式

  / 4

合集下载

晶体的对称性

晶体的对称性

对称性与人类思维方式的联系
对称性思维方式是人类认知世界的一 种重要方式。人们习惯于将事物进行 对称性的分类、比较和思考，从而更 好地理解和把握事物的本质和内在规 律。
VS
对称性思维方式在科学研究和工程技 术中也发挥着重要作用。科学家们利 用对称性原理探索自然界的奥秘，解 决各种复杂的科学问题。工程师们则 利用对称性设计各种结构，提高产品 的稳定性和可靠性。
晶体的对称性
• 对称性的基本概念 • 晶体中的对称元素 • 对称性和晶体结构 • 对称性在化学中的运用 • 对称性与生物学的关系 • 对称性的哲学思考
01
对称性的基本概念
Hale Waihona Puke 称性的定义对称性是指一个物体或图形在某种变 换下保持不变的性质。在晶体学中， 对称性是指晶体在空间变换下保持不 变的性质。
对称性可以通过对称操作来描述，对 称操作是指将晶体进行刚性旋转、平 移、反演等变换后仍能恢复原状的操 作。
对称性的分类
晶体可以根据其对称性进行分类，常 见的晶体分类包括立方晶系、四方晶 系、六方晶系等。
VS
不同晶系的晶体具有不同的对称性， 晶体的对称性与其内部原子或分子的 排列方式密切相关。
对称操作的数学表达
对称操作可以用数学矩阵来表示，通过矩阵变换可以描述晶体的对称性。
对称操作的数学表达包括旋转矩阵、平移矩阵、反演矩阵等，这些矩阵可以用来描述晶体在空间中的 变换。
02
晶体中的对称元素
点对称元素
定义
01
点对称元素是晶体中以某一点为中心的对称操作，包括旋转、
反演、反映等。
描述
02
点对称元素在晶体中起着关键作用，它们决定了晶体的空间群
对称性在生物医学中的应用

晶体结构的对称性

晶体结构的对称性

滑移面—滑移反映操作：由反应与平移组成的复 合对称操作。根据滑移方向的不同分为3类。第 一类轴线滑移面a(或b,c)：如图虚线所示，对应的 操作为反映后，再沿a(或b,c)轴方向平移a/2（或 b/2,c/2)；第二类对角 5 线滑移面n:如图B所 示。实点和虚点分别 4 a 3 是位于纸面的上方和 下方，且距离相等处。 对应的操作使反映后 a 2 沿a轴方向移动a/2,再 沿b轴方向移动b/2,即 1' 1 b 反映后又平移a/2+b/2
分子对称性与警惕宏观对称性对照表
分子对称性 晶体宏观对称性
对称操作及 其符号 旋转L(a) 反映M 倒反I 对称元素及其 对称操作及其 对称元素及 符号 符号 其符号 旋转 对称轴C 旋转轴n 对称面s
n
反映 反演 旋转反映
反映面或镜 面m 对称中心i 反轴
对称中心i 象转轴Sn
旋转倒反 L(a)I
1.2 晶体结构的对称性
1.2.1 晶体的对称元素和对称操作
晶体结构最基本的特征是具有空间点阵结构。 晶体的点阵结构使晶体的对称性和分子的对称性 有差别。分子结构的对称性是点对称性，只有4种 类型的对称元素和对称操作。 （1）旋转轴—旋转操作； （2）镜面—反映操作； （3）对称中心—反演操作； （4）反轴—旋转反映操作。 晶体的点阵结构，包括平移的对称操作。一方面 使晶体结构的对称性在上述点对称性的基础上还 增加下列3种类型的对称元素和对称操作。
对同一晶体，在划分平行六面体时，由于选择 向量的大小和方向不同，有许多划分方法，也就 能找到多种不同形状的晶胞。这些晶胞基本分为 二类：素晶胞和复晶胞。素晶胞包含的内容实质 上就是结构基元。若不考虑其他因素，任何晶体 均可划分为素晶胞。如图： 晶胞的基本要素：一个是晶胞的大小和形状， 可用晶胞参数（a,b,c,a,b,g）表示；另一个是晶 胞中原子的位置，通常用分数坐标（x,y,z)表示。 晶胞参数的定义与空间点阵的参数完全相同。 根据a,b,c,选择晶体的坐标轴X,Y,Z，使它们分别 和向量a,b,c平行。因此将a,b,c表示的方向也叫 晶轴。

1-3 晶体对称性

1-3 晶体对称性
2
2
1 2 3 4 6 2 2 6 4 6
示
平行 斜插纸 纸面 面
二、宏观对称性的组合关系
1. 如果晶体中有两个或两个以上的镜面相交，则每两 个镜面的交线必定是一个对称轴，而对称轴的转角比 定时镜面夹角的二倍。
镜面夹角 180° 90° 60° 45° 30°
旋转轴转 角
360°
180°
120°
90°
Th
Td
O
Oh
晶类（点群）符号 国际符号（全） 国际符号（缩）
1 I（1）
1 I（1）
m
m
2
2
2/m
2/m
3
3
3
3
3m
3m
32
32
32/m
3m
2mm
mm
222
222
2/m2/m2/m
mmm
23
23
2/m3
m3
43m
43m
432
43
4/m32/m
m3m
全对称要素组合
I m(2)
2 2mI
3 3(3I) 33m 332 3323m(3323mI) 23m
三、平移群、布拉菲点阵 例：四方晶系
C→P
F→I
4
晶系 三斜 单斜
菱形
正交
立方
最低对称要素 无
一根二次旋转轴2 或旋转－反演轴2
一根三次旋转轴3 或旋转－反演轴3
三根相互垂直的旋 转轴32或旋转－反 演轴32
四根三次旋转轴43
熊夫列斯符号
C1 Ci（S2） Cs（C1h）
C2 C2h C3 C3i（S6） C3V D3 D3d C2V D2（V） D2h（Vh） T

第六章 6.2 晶体结构的对称性

第六章 6.2 晶体结构的对称性
2 2 2 1 2
范氏半径 (层间分子间距离 平均值)
426.9 441.2 217 pm ~~~ 218pm 4
48
分子形状的构建（分子的大小与形状） 分子长 键长+2×范德华半径 = 272+2×218 = 708 pm 最大处直径
2×范德华半径 = 2×218 = 436 pm
晶体体积及晶体密度的计算
1. 晶体的宏观对称元素
晶体的理想外形在宏观观察中表现出来的对称 元素，称为晶体的宏观对称元素。
自然界中复杂条件下形成的晶体，多数不具有理想外形，不是 单晶而是多晶(其中不是同一空间点阵贯穿始终)；即使是单晶，多 数也不具有理想外形：
天 然
矿
物
晶
体
人工培养的晶体，外形可能随生长条件而变，
通过严格的条件控制，可生长出外形相当完美的单
若某一方向存在镜面，则是与该方向垂直的镜面；
若在某一方向同时存在旋转轴（或反轴）与镜面时, 则用分数 形式来表示,将n（或n ）记在分子位置, 将m记在分母位置. 例：立方晶系： 第32号点群：Oh— 4 3 2
其国际符号的意义：
m
m
第一位表示：在与a平行方向有一四重轴，与a垂直的方向有一镜面。 第二位表示：在与 a+b+c （体对角线）平行方向上有一三重反轴。 第三位表示：在与a+b（面对角线）平行方向有一个二重轴和与之垂 直的方向有一镜面。
晶体的旋转轴仅限于 n=1, 2, 3, 4, 6. 不可能出现 5及大于6的轴次, 这是晶体的点阵结构所决定的.
9
轴 次 定 理 的 数 学 证 明
证明
B' B ma 2a cos 2 n
A‘

07-2.3晶体的对称性

07-2.3晶体的对称性
2.3.2.1 点群
定义：点群是指一个晶体中所有点对称元素的集合。 点对称操作的集合称为点群。
晶体可能存在的对称类型可通过宏观对称元素在一点 上组合运用而得出。
点群在宏观上表现为晶体外形的对称。利用组合定律 可导出晶体外形中只能有32种对称点群。
点群可以用对称元素相结合而导出，在不破坏原有对称的
前提下，结合方式有n/m (表示m⊥n，镜面垂直于n次旋转轴)， nm (表示m∥n，镜面包含n次旋转轴)， n/mm或n/m m(第
晶体绕某一轴回转能复原n次，就称之为n次对称轴。 晶体中实际可能存在的对称轴有五种，并用符号1，
2，3，4，和6来表示。
旋转角 n名称 符号
360 180 120 90 60 度
1
2 3 4 6 次轴
1
2 356
2. 对称面
立方晶系{100} {110}
晶体通过某一平面作 镜像反映而能复原， 则该平面称为对称面 或镜面，用符号m表示。 对称面通常是晶棱或 晶面的垂直平分面或 者为多面角平分面， 且必定通过晶体几何
晶体基本的对称操作有点对称操作和平移对称操作。
在对称操作过程中保持空间至少有一个不动点的操作 称为点对称操作。在一般的对称操作过程中，空间有许多 点在动，但操作前后状态一样。 如旋转，反演，平面反映 均为点对称操作。
用点对称操作ห้องสมุดไป่ตู้组合可以描述有规则几何外形的单晶 体所具有的点对称性，但许多金属单晶体虽然不一定具备 规则的几何外形，但它们相应的点对称性却仍然存在。
180º与P3点重合，再经O点反 演而与P’重合，则称BB‘为2
次旋转—反演轴。
旋转—反演轴有1，2，3，4
和6次五种，分别以国际符号
_ ____

晶体的对称性

晶体的对称性

晶体对称性
晶体性质
晶体具异向性，并不排斥在某些特定的方向上性质相同。

这是因为在晶体的格子构造中，这些方向质点的排列是一样的，这就是晶体的对称性，表现在晶体外形上，即相等的晶面、晶棱和角顶有规律地重复出现。

晶体的对称性是晶体极其重要的性质。

中文名称
晶体对称性
英文名称
symmetry of crystal
定义
根据晶体其对称元素进行对称操作，能使其等同部分产生规律性的重合特性。

应用学科
材料科学技术（一级学科），材料科学技术基础（二级学科），材料科学基础（三级学科），材料组织结构（四级学科）
晶体的格子构造是晶体实现最小内能的结果。

由于晶体具有最小的内能，所以处于相对稳定的状态，这就是晶体的稳定性。

晶体只有在得到外来能量时，才能破坏其稳定性，有使之向非晶质转化。

这一点可以从晶体的加热曲线得到证明。

1-晶体结构及其对称性(研)

A 原子的右侧一定距 离处有一个碳原子而左 侧没有，但是B 原子则 相反。
二维蜂窝格子 (非布拉菲格子)
如果将A、B两个原子看作为一 个基元，则点阵结构就如前页所示 ，格子就是布拉菲格子了。
14种布拉菲格子:
1.简单三斜； 2.简单单斜， 3.底心单斜； 4.简单正交， 5.底心正交， 6.体心正交， 7.面心正交； 8.六角； 9.三角； 10.简单四方， 11.体心四方； 12.简单立方， 13.体心立方， 14.面心立方。
（3）金刚石结构（ diamond ）：
碳的同素异构体。 经琢磨后的金刚石又称钻石。 无色透明、有光泽、折光力极强，最硬的物质。
金刚石结构是复式晶格结构，基元中有两个碳原子A、B， 布拉菲格子是面心立方。
或可视为两个面心立方子晶格，沿体对角线平移1/4 体对角 线长度套构而成，如图所示．
金刚石晶体的配位数是4, 这4个碳原子构成一个 正四面体，碳-碳键角为109º28´。
例如，简立方晶格的几个晶面表示。
注意：晶向指数与晶面指数的表示差异。
晶向指数表示晶列取向，用中括号[…]表示； 晶面指数表示晶面方向，用圆括号(…)表示。
§1.3 倒格子
一、定义
晶体的布拉菲点阵由三个原胞基矢 、a1 、a2 来a描3 述．
定义三个新矢量：
b1
2
(,a2
其中： a1 轴[100]， a2 轴[010]， a3 轴[001]，
a1 轴 [1 00] 等，其中－1的负号放在1的上面。
二、晶面和晶面指数
任意三个不共线的格点，构成一个晶面．
与晶列性质类似，晶面也具有下面三个方面的性质： 任一晶面上都有无穷多个格点； 任一晶面都有无穷多个互相平行的晶面，构成一个晶面簇； 每一个晶面簇都将晶体中所有的格点包含无遗．

晶体对称性

晶体对称性晶体对称性是晶体学研究的一个重要组成部分，它是晶体结构的关键，可以解释晶体的外观、性质以及界面问题。

其中，最常见的是空间群，它用数学表示法确定变换的形式。

接下来，让我们来更多地了解晶体对称性：一、空间群1. 什么是空间群：空间群是一种变换群，也是对称性理论的基础，可以描述物体在特定坐标系中的集合子空间上的空间操作。

举个例子，如果一个物体只可以在空间系中做180°旋转，那么它就只具有一种（即旋转）拓扑群。

2. 空间群划分：空间群可以根据对称性来划分，主要包括有限对称群、无限对称群和单调对称群三类。

其中，有限对称群表示法子群的形状、大小或空间构造不变；无限对称群指的是无限种变换，其轴心、空间点或空间构造不变；而单调的对称群是单一的元素组成的，在该空间群中任何对称性都不变。

二、对称性1. 什么是对称性：对称性是空间群的基础，一般来说，它表示物体在某种坐标下有特定形状和空间操作的属性，也可以用数学表示法来表达这种特征。

2. 对称性的类型：对称性的类型可以分为四大类，分别是正交对称性、立体对称性、平面对称性和点对称性。

其中，正交对称性主要涉及空间中的空间坐标变换，立体对称性是指物体在立体坐标系下的操作，而平面对称性是指物体在平面坐标系下的操作，而点对称性则是指物体在特定空间构造下的操作。

三、晶体对称性1. 晶体对称性是什么：晶体对称性是晶体学研究的一个重要组成部分，它涉及到晶体结构的外观、性质以及界面问题的解释。

2. 晶体对称性的应用：晶体对称性可以用来研究和设计多种材料，如金属、半导体、有机分子晶体、生物晶体等，它们是将材料化学性质同物理性质关联起来，从而更好地理解材料的特性。

此外，晶体对称性也可用于分类、指导结构分析以及材料的设计和合成等。

四、总结从上文可以看出，晶体对称性是一个非常重要的概念，它不仅仅可以用来描述物体的形状、大小和空间结构，而且可以应用于许多不同的领域，如材料的研究与设计等。

晶体的结构及其对称性

配位数：8
原子半径：
r
3
V
atom
4 3 a 3 4
3 a 4
V
bcc

a
3
Body centered cubic lattice
原子数： 堆积密度：
8
1 1 2 8
atom
f V
2
V

bcc
3 8
具有此结构的金属原子：碱金属Li、Na、K、Rb、Cs；难熔金 属W、Mo、Nb、Ta等。
的平移对称性。
• 基元按点阵排布得到晶体结构： <点阵>+<基元>=<晶体结构>
三、基矢和元胞 对于一个给定的点阵，总可以选择三个不共面的基本平移矢量������1 、������2 、������3
（称为点阵的基矢），使任意一个结点
3
������������ =������1 ������������ +������2 ������������ +������3 ������������ =
关于常见晶体结构的一些定义： • 配位数：每个原子周围的最近邻原子数 • 堆积密度：原子球的体积与其所占据的有效空间体积之比
（1）简单立方(sc)晶体结构
配位数：6
a
3
原子半径： r 2
V
atom
4 3
a 2
V
原子数： 堆积密度：
sc

a
3
Simple cubic lattice
• 面心立方(fcc)晶体结构
配位数：12
原子半径：
r
3
4 2 V fcc V atom 3 4 a 1 1 8 6 4 原子数： 8 2

结构化学晶体结构的对称性和基本定理


点击按钮观察动画.注意：反映滑移操作中
的“反映”是虚操作，可想象而难以实际表现, 故动画 中用幻影逗号的移动来模拟反映，请勿误解！
8.2.2 晶胞
设想把点阵放回晶体中去， 将把晶体切分成并置的平行六面 体小晶块，每个空间格子对应一 个小晶块. 这种小晶块就是晶胞, 是代表晶体结构的最小单元.
晶胞参数
NaCl型晶体
原子的分数坐标： A: 0 0 0
0 1/2 1/2 1/2 0 1/2 1/2 1/2 0 B: 1/2 0 0
0 1/2 0 0 0 1/2 1/2 1/2 1/2 结构基元: A-B （每个晶胞中有4个结构基元）
CsCl型晶体
原子的分数坐标： A: 0 0 0 B: 1/2 1/2 1/2
为什么要考虑带心格子?
立方面心格子，若按左图取素格子只能表现三方对称性；若取右图 所示的复格子就表现出立方对称性(格子选取方式不能改变点阵结构的对 称性,但点阵固有的较高对称性在素格子上可能被掩盖)：
14种布拉维格子之一：立方简单（cP）
14种布拉维格子二：立方体心（cI）
14种布拉维格子三：立方面心（cF）
晶胞参数:
a、b、c α、β、γ
晶
胞
两
要
（1）晶胞的大小、型式
素
晶胞的大小可由晶胞参数确定，晶胞的型式是
指素晶胞或复晶胞.
（2）晶胞的内容
晶胞中原子的种类和位置. 表示原子位置要用 分数坐标.
分数坐标
晶胞中原子P 的位置用向量OP=xa+yb+zc代表. x、y、z
就是分数坐标，它们永远不会大于1.
14种布拉维格子之八：正交简单（oP)
14种布拉维格子之九：正交体心（oI)
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

晶体的对称性
1. 晶体的宏观和微观对称性
晶体的对称性最直观地表现在其几何外形上，由于晶体外形为有限的几何图形，故晶体外形上所体现的对称性与分子一样为点对称性，称为宏观对称性。

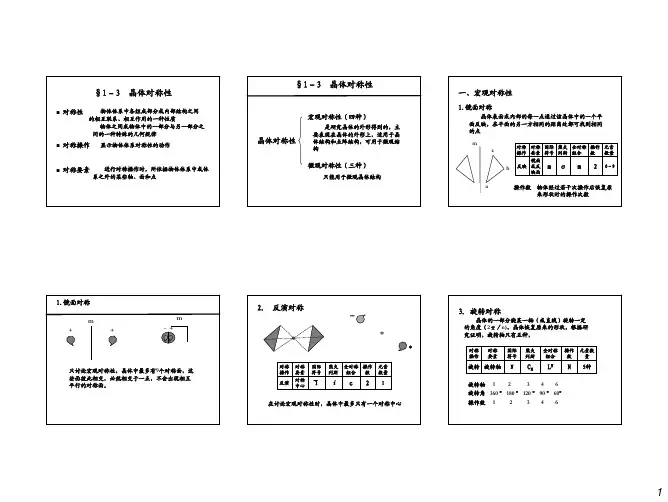
有四种类型的对称操作和对称元素
旋转旋转轴
反映反映面(镜面)
反演对称中心
旋转反演反轴
由于晶体内部结构为点阵结构，点阵结构是一种无限的几何对称图形。

故晶体结构具有这种基本的空间对称性(通过平移对称操作能使点阵结构复原)，常称为晶体的微观对称性。

有三种类型的对称操作和对称元素
平移点阵
螺旋螺旋轴
滑移滑移面
2. 晶体和晶体结构对称性的有关定理
晶体和晶体结构的对称元素及相应的对称操作有上述七种。

晶体中点阵与对称元素的制约关系为：
对称面和对称轴的取向定理
在晶体结构的空间点阵图形中，对称轴必与一组直线点阵平
行，并与一组平面点阵垂直；对称面则必与一组直线点阵垂
直，并与一组平面点阵平行。

(对称轴包括旋转轴、反轴和螺
旋轴；对称面包括反映面、滑移面)
∙对称轴的轴次定理
在晶体结构中存在的对称轴，其轴次只能为1、2、3、4、6
这五种。

3. 7个晶系和32个晶体点群
∙根据晶体的对称性，可将晶体分为7个晶系，每个晶系有它自己的特征对称元素。

晶体特征对称元素
立方晶
系
四个按立方体的对角线取向的3重轴
六方晶
系
唯一的6重轴
四方晶
系
唯一的4重轴
三方晶
系
唯一的3重轴
正交晶系三个互相垂直的2重轴或二个互相垂直的对称
面
单斜晶
系
一个2重轴或对称面
三斜晶
系
无
∙由于晶体的对称性定理，限制了对称轴的轴次只能为1、2、
3、4、6；又由于反轴中只有4重反轴是独立的对称元素，所
以在晶体的宏观对称性中，只能找到8个独立的对称元素：
1、2、3、4、6、m、i、。

∙与分子所含的对称元素相比，晶体中所含的对称元素有限，这八个对称元素按一定的组合规则组合后只能产生32个对称类型(对称元素系)，每个对称类型所具有的对称元素所对应的对称操作构成一个群。

由于晶体的宏观外形为有限图形，故各种对称元素至少要相交于一点，故称为32个晶体点群。

∙对于晶体点群，除了用和分子点群一样的符号(Schönflies)表示外，还用晶体点群的国际上通用的符号——国际符号表示。

国
际符号是按晶系不同，依次在三个不同方向上将晶体所具有的对称元素表示出来。

且晶系不同规定的方位不同，见下表：
晶系
三个位置所代表的方向
第一方位第二方位第三方位
立方晶系a a+b+c a+b
六方晶系c a2a+b
四方晶系c a a+b
三方晶系a+b+c a-b-
三方晶系*c a-
正交晶系a b c
单斜晶系b--
三斜晶系---
*为取六方晶胞
例如：立方晶系的O
h
点群的国际符号：
还可以记为m3m。

4. 230个空间群
∙由于晶体的内部结构为点阵结构，所以由点阵结构所反映出的对称性是晶体外形结构最根本的对称性。

∙但由于从晶体外形上看，由螺旋轴或滑移面产生的平移往往被晶体的均匀性所掩盖，故从晶体外形上只能观察到旋转轴或反映面的存在。

在同一晶体中轴次相同的螺旋轴与旋转轴、滑移面与反映面均为同形对称元素(两对称元素同向)，相应的对称操作除平移外其它部分相同。

例如：如果晶体结构中有一个二重螺旋轴21，则宏观晶体在这个方向上将显示一个二重旋转轴2，而且每一点上都显示出这样的二重旋转轴。

根据这一同形原理。

在32个晶体点群的基础上，按一定的原则和方法，加上被均匀性掩盖的各类空间平移操作，便可以推引出与32个晶体点群同形的230个空间群。

这230个空间群描述了晶体结构中所可能有的230种不同类型的微观对称
性。