戴维南定理汇总

电路中的戴维南定理解析电路中的戴维南定理是电路分析中常用的一种方法，它可以简化复杂的电路结构，使得我们能够更轻松地计算电流和电压。

本文将对戴维南定理进行解析，并探讨其在电路分析中的应用。

一、戴维南定理的基本原理戴维南定理，也叫戴维南-儒金定理，是由法国数学家戴维南和德国物理学家儒金独立提出的。

该定理提供了一种将复杂电路简化为等效电路的方法，从而更容易进行电路的分析和计算。

戴维南定理的基本原理可以总结为两点：1. 任何一个线性电路都可以用一个等效电动势和一个等效电阻来代替。

2. 这个等效电阻等于原始电路中所有电源电动势与电压源的内阻之比的总和。

二、戴维南定理的数学表达在数学上，戴维南定理可以通过以下公式来表达：I = E/R其中，I是电路中的电流，E是电路中的总电动势（电源的电动势之和），R是电路中的总电阻（包括电路中的电阻和电源的内阻之和）。

根据这个公式，我们可以计算电路中的电流，从而更好地了解电路的特性和性能。

三、戴维南定理的应用举例为了更好地理解戴维南定理在实际电路中的应用，下面将通过一个简单的电路示例进行说明。

假设有一个由三个电阻和一个电压源组成的混合电路，我们想要计算电路中的电流。

首先，我们可以根据戴维南定理将这个复杂的电路简化为一个等效电路。

根据戴维南定理，我们可以将这个复杂的电路简化为一个等效电动势和一个等效电阻。

其中，等效电动势等于电源的电动势之和，等效电阻等于电路中的电阻和电源的内阻之和。

然后，我们可以根据简化后的等效电路计算电路中的电流。

根据戴维南定理的公式，我们可以通过总电动势除以总电阻来计算电流的大小。

通过这个简单的示例，我们可以看到戴维南定理在电路分析中的应用。

它可以将复杂的电路结构简化为一个等效电路，从而方便我们进行电流和电压的计算。

四、戴维南定理的优点和局限性戴维南定理作为一种电路分析方法，具有以下优点：1. 简化电路结构：戴维南定理能够将复杂的电路结构简化为一个等效电路，从而减少计算的复杂性。

戴维南定理的公式
一、戴维南定理的概述
戴维南定理（Thevenin"s Theorem）是电路分析中一个非常重要的定理，它用于简化复杂电路的计算。

该定理指出，一个线性电阻网络可以通过一个等效的电压源和一个等效的电阻来实现相同的电压和电流分布。

二、戴维南定理的公式
戴维南定理可以用以下公式表示：
Vth = Vout - IR
其中，Vth表示等效电压源的电压，Vout表示原电路中的输出电压，I表示等效电路中的电流，R表示等效电阻。

三、戴维南定理的证明
戴维南定理的证明可以通过构建等效电路来进行。

首先，从原电路中剪切出一段包含电压源和电阻的电路，然后通过基尔霍夫定律和欧姆定律逐步推导得出等效电压源和等效电阻的关系式，最终得到戴维南定理的公式。

四、戴维南定理的应用
戴维南定理在电路分析中有广泛的应用，如：
1.简化电路计算：通过将复杂电路转化为等效电路，可以简化计算过程，提高计算效率。

2.电路设计：在设计电路时，可以使用戴维南定理来选择合适的元器件，以满足电路性能要求。

3.故障诊断：在电路出现故障时，可以通过戴维南定理构建等效电路，分
析故障原因并进行修复。

五、戴维南定理的扩展
戴维南定理还可以扩展到含有多个电压源和电阻的电路中，此时需要分别计算每个电压源单独作用时的等效电阻，然后根据戴维南定理进行求解。

总之，戴维南定理是电路分析中一个非常重要的定理，通过掌握该定理，可以简化复杂电路的计算，提高电路设计的效率，并为故障诊断提供便利。

戴维南定理总结在数学领域中，存在一条著名的定理，它以法国数学家戴维南的名字命名。

戴维南定理是一个关于三角形边长关系的重要定理，它向我们展示了三角形的一些惊人性质。

下面我们将对戴维南定理进行总结和探讨。

戴维南定理的内容非常简洁明了：任意三个正数a、b、c，满足a+b>c、b+c>a和c+a>b的条件时，它们可以构成一个三角形。

这个定理被称为不等式定理，它提供了判断三个边长是否能够构成三角形的有效方法。

为何戴维南定理如此重要？首先，它为我们理解三角形提供了一种便捷的途径。

通过该定理，我们可以更好地理解三个边长之间的关系，从而我们能够在三角形的基础上进行更多推导和证明。

其次，该定理广泛应用于几何学、三角学以及计算机科学等领域。

在构建计算机图像、建模等方面，对三角形进行有效判定非常关键。

另外，戴维南定理还帮助我们进一步了解三角形的性质。

它揭示了三个边长之间的关系与三角形的内角、外角大小之间存在着密切联系。

例如，在一个三角形中，较长的边对应的内角一定大于较短边对应的内角。

这是因为根据戴维南定理，较短边对应的内角必须小于两个边之和，而较长边对应的内角却可以大于另外两个边之差。

戴维南定理不仅仅是一个简单的判定定理，它引出了许多深入的数学思考。

例如，对于给定的边长a、b、c，我们如何确定它们所构成的三角形的类型？根据戴维南定理，如果a=b=c，那么三角形是等边三角形；如果a=b或者a=c或者b=c，那么三角形是等腰三角形；如果两边之和等于第三边，那么三角形是退化成一条直线；还有更多的情况，我们可以通过对戴维南定理的进一步研究来发现。

在实际应用中，戴维南定理也可以被推广到更高维度的几何形状。

例如，我们可以将其应用于四边形的判定。

对于四个边长a、b、c、d，满足a+b+c>d、b+c+d>a、c+d+a>b和d+a+b>c的条件时，它们可以构成一个四边形。

通过类似的思路，我们可以推广至更高维度的几何形状，丰富了戴维南定理在不同几何形状中的应用。

戴维南定理的公式【实用版】目录1.戴维南定理的概述2.戴维南定理的公式推导3.戴维南定理的公式应用4.总结正文一、戴维南定理的概述戴维南定理，又称狄拉克定理，是由英国物理学家保罗·狄拉克于1927 年提出的。

该定理主要应用于量子力学中的狄拉克方程，对于研究电子在电磁场中的运动具有重要意义。

戴维南定理给出了一个计算电子在电磁场中作用力的简便方法，其核心思想是将电磁场中的电子运动问题转化为一个在势场中的运动问题。

二、戴维南定理的公式推导为了更好地理解戴维南定理，我们首先来看一下狄拉克方程。

在经典力学中，电子在电磁场中的运动满足以下方程：F = - (Ψ/t) * (/2m) * Ψ - (/2m) * Ψ * (Ψ/t)其中，F 表示电子所受的电磁场力，Ψ表示电子的波函数，t 表示时间，m 表示电子质量，表示约化普朗克常数，表示梯度算子。

在量子力学中，电子的运动满足狄拉克方程，可以将其写为：HΨ = EΨ其中，H 表示哈密顿算子，E 表示电子的能量。

接下来，我们考虑将狄拉克方程中的电磁场作用力表示为势能的形式。

根据波函数的定义，可以将Ψ表示为势能函数φ的梯度，即Ψ = φ。

将此代入狄拉克方程，可以得到：HΨ = H(φ) = E(φ)对两边求散度，得到：HΨ = E(φ)根据散度算子的性质，可以将上式化简为：- (Ψ/t) * φ = - (E/t) * φ再根据势能的定义，可以将上式写为：- (Ψ/t) * φ = - (U/t) * φ其中，U 表示势能。

由此可以看出，电子在电磁场中的运动满足势能定理。

也就是说，电子在电磁场中所受的力可以表示为势能的负梯度。

这就是戴维南定理的公式表达。

三、戴维南定理的公式应用戴维南定理的公式可以为计算电子在电磁场中的运动提供极大便利。

例如，当电子在均匀电场中运动时，可以根据戴维南定理求出电子所受的力。

假设电子的势能函数为 U = -qφ，其中 q 表示电子电荷，φ表示电势。

简述戴维宁定理内容
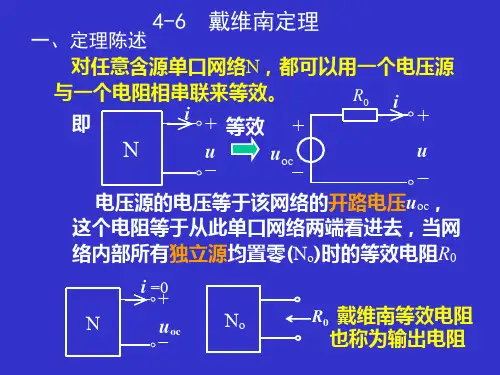
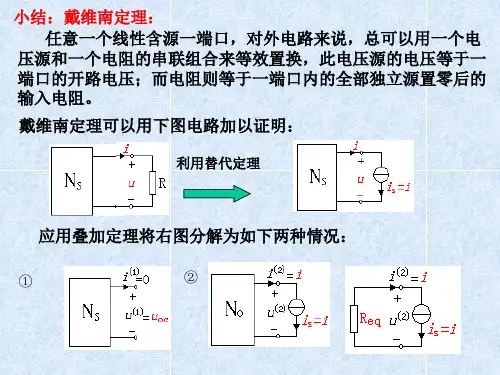
一、戴维宁定理（也称为戴维南定理）：任何一个线性含源一端口网络，对外电路来说，总可以用一个电压源和电阻的串联组合来等效置换；此电压源的电压等于外电路断开时端口处的开路电压Uoc，而电阻等于一端口的输入电阻（或等效电阻Req）。

二、戴维南定理（又译为戴维宁定理）又称等效电压源定律，是由法国科学家L，C，戴维南于1883年提出的一个电学定理。

由于早在1853年，亥姆霍兹也提出过本定理，所以又称亥姆霍兹-戴维南定理。

其内容是：一个含有独立电压源、独立电流源及电阻的线性网络的两端，就其外部型态而言，在电性上可以用一个独立电压源V 和一个松弛二端网络的串联电阻组合来等效。

在单频交流系统中，此定理不仅只适用于电阻，也适用于广义的阻抗。

戴维南定理在多电源多回路的复杂直流电路分析中有重要应用。

归纳总结戴维南定理
戴维南定理是一个著名的结构力学定理，它的发现是由英国工程师Adriano Davinin 1864年发明的。

它说明了一个物体的内部结构和其外部形状之间的联系。

定理指出，一个物体的内部结构是它能承受外力的能力的重要因素。

戴维南定理解释了当施加某种外力时，一个物体的内部结构如何影响它的行为。

它指出，当一个柱子的立柱连续的，它的剪切强度就大些，而反之，如果它的立柱不是连续的，就会减小剪切强度。

戴维南定理的应用也有很多，一个最重要的应用是工程设计。

它可以帮助工程师设计出能承受特定荷载和外力的构件。

该定理还有助于设计更坚固、更稳定的机械设备和建筑物。

另一个重要的应用是材料科学。

它有助于确定一个材料在特定外力作用下的疲劳行为和抗压强度。

此外，它也有助于确定一个材料在环境温度和湿度的变化下的强度变化。

总的来说，戴维南定理是一个重要的工程和材料科学原理，它指导着设计构件的大量工程设计、机械设备设计和建筑物设计，它也有助于确定一种材料的抗压强度。

它的应用是在现代工程设计中非常重要的，它也是现代科学和技术发展之重要一环。

- 1 -。

戴维南定理验证归纳总结戴维南定理（Davidson's Theorem）是一个在算法设计和图论中广泛应用的重要理论。

它是由著名计算机科学家戴维南（Davidson）提出的，并被证明具有广泛的适用性和有效性。

在本文中，我们将对戴维南定理进行验证，并对其进行归纳总结。

1. 戴维南定理的基本概念戴维南定理是关于有向图中是否存在一个环的问题。

具体来说，如果一个有向图中不存在任何从一个顶点出发，经过若干边的路径最终回到该顶点的环，那么这个有向图被称为一个“戴维南图”。

戴维南定理则指出，一个有向图是戴维南图等价于这个有向图的特征矩阵可以通过最优化调整，使得其主对角线都是非负的。

2. 验证戴维南定理为了验证戴维南定理的正确性，我们可以按照以下步骤进行：步骤一：根据给定的有向图，绘制其特征矩阵。

步骤二：检查特征矩阵中是否存在负数元素。

如果存在负数元素，则进行第三步；如果不存在负数元素，则该有向图是一个戴维南图。

步骤三：通过最优化调整特征矩阵，使得其主对角线上的元素都变为非负数。

步骤四：再次检查特征矩阵中是否还存在负数元素。

如果存在负数元素，则该有向图不是一个戴维南图；如果不存在负数元素，则该有向图是一个戴维南图。

通过以上步骤的验证过程，我们可以得出结论，从而验证戴维南定理的正确性。

3. 戴维南定理的应用戴维南定理在算法设计和图论中有着广泛的应用。

它提供了一种有效的方法来判断一个有向图是否存在环，从而可以在许多实际问题中得到应用。

例如，在任务调度中，通过验证某个任务调度图是否是一个戴维南图，可以判断该任务调度是否存在死循环等问题，从而保证任务调度的正确性和可行性。

此外，戴维南定理还在电路设计和网络优化等领域有着重要的应用。

通过验证电路图或网络拓扑图是否是一个戴维南图，可以有效地避免电路或网络中出现环路问题，提高系统的可靠性和性能。

4. 归纳总结通过对戴维南定理的验证过程和应用分析，我们可以得出以下结论：（1）戴维南定理是一个有效的方法来判断一个有向图是否存在环。

戴维南定理实验总结简介戴维南定理是数学中一个重要的定理，它提供了一种判断一个给定的二元关系是否为等价关系的方法。

戴维南定理实验是通过对一组数据进行分析和处理，验证戴维南定理的正确性和适用性。

重要观点1.戴维南定理：给定一个非空集合A和定义在A上的二元关系R，R是A上的等价关系当且仅当R满足自反性、对称性和传递性。

2.自反性：对于任意元素a∈A，有(a, a)∈R。

3.对称性：对于任意元素a, b∈A，若(a, b)∈R，则(b, a)∈R。

4.传递性：对于任意元素a, b, c∈A，若(a, b)∈R且(b, c)∈R，则(a,c)∈R。

关键发现在戴维南定理实验中，我们使用了一个具体的例子来验证戴维南定理。

假设有一组数据集合A={1, 2, 3}，并定义二元关系R={(1, 1), (2, 2), (3, 3), (1, 2), (2, 1)}。

下面我们通过分析这个数据集合来验证戴维南定理：1.自反性：对于任意元素a∈A，有(a, a)∈R。

在我们的例子中，(1, 1)、(2,2)和(3, 3)满足自反性。

2.对称性：对于任意元素a, b∈A，若(a, b)∈R，则(b, a)∈R。

在我们的例子中，(1, 2)满足对称性，因为(2, 1)也在关系R中。

3.传递性：对于任意元素a, b, c∈A，若(a, b)∈R且(b, c)∈R，则(a,c)∈R。

在我们的例子中，虽然存在(a, b)=(1, 2)和(b, c)=(2, 1)，但是不存在(a,c)=(1,1)，所以不满足传递性。

通过以上分析可以得出结论，在给定的数据集合A和二元关系R下，并不满足戴维南定理。

因此，我们可以推断出这个二元关系不是等价关系。

进一步思考戴维南定理实验引发了一些进一步思考和探索的问题：1.如何构造一个等价关系？在本实验中，我们没有找到一个满足戴维南定理的等价关系。

因此，我们可以继续探索如何构造一个满足戴维南定理的等价关系，并进一步研究等价关系的性质和应用。

戴维南定理内容
戴维南定理是由英国数学家约翰·戴维南在1839年提出的一个数学定理。

这个定理在20世纪早期推广开来，并被广泛研究。

它表明所有奇数都是质数的结论，这一结论被称为戴维南定理。

戴维南定理关于奇数和质数的本质关系，可以用数学集合论的语言简单表达如下：质数集合p=奇数集合o。

也就是说，集合o中的所有奇数都是质数。

戴维南定理的最早原始推导可以追溯到1839年，由约翰·戴维南提出的。

他的原始推理是
基于古典数论的概念，最主要的思想是“因子分解法”，他认为可以将所有奇数都分解为质
因数来分解。

戴维南定理预言的奇数的概念在很长时间里，一直是数学的基础。

在浩瀚的数学建模中，这一定理几乎可以说成是有根本性意义的。

它被广泛应用于不同领域，如分形论，抽象代数，拓扑等。

从理论上讲，戴维南定理已经得以进一步验证和发展，它也得到了许多学者的认可，它的实际应用场景也越来越广泛。

因此，戴维南定理已经成为当今数学最重要的基础思想之一。

电路戴维南定理电路戴维南定理（Kirchhoff's Circuit Laws）是电路分析中的基本原理，由德国物理学家戴维南（Gustav Kirchhoff）于19世纪中叶提出。

该定理包括戴维南电流定律（Kirchhoff's Current Law，简称KCL）和戴维南电压定律（Kirchhoff's Voltage Law，简称KVL），它们是电路分析的重要工具，用于描述和分析电路中电流和电压的分布和变化。

戴维南电流定律（KCL）是指在任意一个电路节点（连接两个或多个电路元件的交汇处），进入该节点的总电流等于离开该节点的总电流的和。

换句话说，电流在节点处守恒。

这个定律可以表达为以下公式：∑(I_in) = ∑(I_out)其中，∑(I_in)表示进入节点的总电流，∑(I_out)表示离开节点的总电流。

这个定律基于电荷守恒原理，可以应用于任意复杂的电路网络。

戴维南电压定律（KVL）是指在一个封闭回路中，沿着回路的总电压等于各个元件电压之和。

换句话说，电压在回路中守恒。

这个定律可以表达为以下公式：∑(V_loop) = 0其中，∑(V_loop)表示沿着回路的总电压，它等于各个元件电压之和。

这个定律基于能量守恒原理，可以用来分析电路中各个元件之间的电压关系。

戴维南定律提供了电路分析的基本原理，它们可以应用于直流电路和交流电路的分析。

通过使用KCL和KVL，可以建立电流和电压的方程组，从而求解电路中各个元件的电流和电压。

这对于设计和分析各种电路，如电源电路、放大电路、滤波电路等都非常重要。

总结起来，电路戴维南定律是电路分析的基本原理，包括戴维南电流定律（KCL）和戴维南电压定律（KVL）。

KCL描述了电流在节点处的守恒，KVL描述了电压在回路中的守恒。

通过应用这些定律，可以建立电路方程组，求解电路中各个元件的电流和电压，对电路的设计和分析起到重要的作用。