江苏省金湖县实验中学高中数学 奥赛辅导 二次函数与方程、不等式

江苏省金湖县实验中学高中数学 奥赛辅导 整式的恒等变形 内容：（1）运用运算性质法则。

（2）灵活运用乘公式。

（3）配方法。

（4）应用因式分解。

（5）代换法。

一．（运用性质和法则）1． 设x , y , z 都是整数，且11整除7x+2y-5z , 求证：11整除3x-7y+12z .2． 已知d cx x ax y +++=356，当x = 0 时，y = - 3 ;当x = -5 时，y = 9 , 求当x = 5时 y 的值。

二．（灵活运用乘法公式）3． 计算：()()()()1121212123242+++++ΛΛ4． 设a , b , c 为有理数，且0,0333=++=++c b a c b a .求证：对于任何正奇数n ，都有0=++n n n c b a5． 当1,0222=++=++c b a c b a 时，试求下列各式的值：（1）ab ca bc ++ ；（2）444c b a ++6． 试求x x x x x x +++++392781243被1-x 除的余数。

三．（配方法）7． 证明：当a , b 取任意有理数时，多项式116222++-+b a b a 的值总是正数。

8． 若()()22223214c b a c b a ++=++，求a : b : c . 9． 已知a , b , c , d 为正数，且abcd d c b a 44444=+++，求证： a = b = c = d .11. 解方程：0441212322222=+-++-y y y x y x x12．若a , b , c , d 是整数，且2222,d c n ba m +=+=，求证：mn 可表示成两个整数的平方和。

13．已知2,122=+=+b a b a ，求77b a +的值。

四．（应用因式分解）14．在三角形ABC 中，22216c b a -- 0106=++bc ab （a , b , c 是三角形的三边）， 求证：b c a 2=+15．已知c a bc a b c b ac b a 222222++=++，试求()()()a c c b b a ---的值。

一、利用同类项的定义构造：例1：已知m n m n b a --319991和1079999+-m n a b 是同类项，则.________22=+n m 二、利用二元一次方程的定义构造： 例2：若243724953=+--++n m n m y x 是二元一次方程，则nm 的值等于________. 三、利用方程组的解的定义构造：例3：若⎩⎨⎧==12y x 是方程组⎩⎨⎧=+=-5213by ax y ax 的解，求b a 、的值.四、利用相反数的性质构造：例4：已知a 的相反数是12+b ，b 的相反数是13+a ，则.________22=+b a五、利用非负数性质构造：例5：如果实数y x ,满足()022=++-y x x ，那么.________=y x 六、利用多项式恒等性质构造：例6：已知多项式6823222-+--+y x y xy x 可以分解为()()n y x m y x +-++22的形式，那么.________1123=++n m 七、利用一次方程的解的特征构造：例7：已知关于x 的方程()()()15133+=++-x x b x a 有无穷多个解，那么.________________,==b a 八、取特殊值构造：例8：设b ax x x ++-232除以()()12+-x x 所得的余式为12+x ，那么.________________,==b a 九、弱化某些未知数构造：例9：若,073,0452=-+=++z y x z y x 则.________=-+z y x 十、利用新运算的定义构造：例10：对于实数y x ,定义一种新运算*：,c by ax y x ++=*其中c b a 、、为常数，等式右边是通常的加法与乘法运算.已知：,2874,1553=*=*那么.________11=*。

等式和它的性质（2）教学目的1、掌握等式的两条性质，会用等式的性质将等式进行变形。

做到深入理解，熟练运用。

教学分析重点：等式的两条基本性质的熟练运用。

难点：等式基本性质2，“等式的两边都除以同一个数（除数不能是0）”，在具体运用中学生容易犯错误，尤其是除数为字母表示的数。

突破：理解性质，弄清概念。

教学过程一、复习1、什么是等式？说出等式的两条性质。

2、按照下列条件，写出仍能成立的等式，并说明根据等式的哪一条性质：（1）若-a+b-1=-a+1,两边都加上a+1（2）若-3m=1, 两边都除以－3，（3）若x+1=0, 两边都除以x，（4）若u－2=0, 两边都除以u，这里是为了强调性质2中的特殊点，即不可以除以0，不可以除以一个整式。

二、新授1、在上节学习的基础上，本节课通过练习进一步巩固和熟练。

例1 在下列横线内用符号“＝”或“≠”连接：（1）如果x+a=b，那么x＿＿b－a；（2）如果x=y，那么y ＿＿x，x－y＿＿0；（3）如果x=y，y=5，那么x＿＿5；（4）如果x=3，那么2（x－3）＿＿5（x－3）（5）如果5a=2a，那么a＿＿0.以上都应填上“＝”，通过（2）指出等式的对称性，通过（3）指出等式的传递性，（5）有告诫作用。

例2 按照下列条件，写出仍能成立的等式：（1）由3x =4x－1，两边都减去3x;（2）由a+3=b，两边都乘以m;（3）由mx=my，两边都除以m。

解：（1）0=4x－3x－1; （2）（a+3）m=bm;（3）当m≠0时，x=y,当m=0时，0不能做除数，不能进行变形。

注意：把等式的两边同除以某个字母，要查一下它会不会等于0，字母做除数，字母取值应保证分母不为零。

三、练习P187B：1。

四、小结1、等式的性质课本中有两条，还有等式的对称性和传递性。

五、作业1、P187：B：2，3。

2、基础训练同步练习2。

- 1 - 一、利用同类项的定义构造：例1：已知m n m n b a --319991和1079999+-m n a b 是同类项，则.________22=+n m 二、利用二元一次方程的定义构造： 例2：若243724953=+--++n m n m y x 是二元一次方程，则nm 的值等于________. 三、利用方程组的解的定义构造：例3：若⎩⎨⎧==12y x 是方程组⎩⎨⎧=+=-5213by ax y ax 的解，求b a 、的值.四、利用相反数的性质构造： 例4：已知a 的相反数是12+b ，b 的相反数是13+a ，则.________22=+b a五、利用非负数性质构造：例5：如果实数y x ,满足()022=++-y x x ，那么.________=yx 六、利用多项式恒等性质构造：例6：已知多项式6823222-+--+y x y xy x 可以分解为()()n y x m y x +-++22的形式，那么.________1123=++n m 七、利用一次方程的解的特征构造：例7：已知关于x 的方程()()()15133+=++-x x b x a 有无穷多个解，那么.________________,==b a八、取特殊值构造：例8：设b ax x x ++-232除以()()12+-x x 所得的余式为12+x ，那么.________________,==b a九、弱化某些未知数构造：例9：若,073,0452=-+=++z y x z y x 则.________=-+z y x 十、利用新运算的定义构造：例10：对于实数y x ,定义一种新运算*：,c by ax y x ++=*其中c b a 、、为常数，等式右边是通常的加法与乘法运算.已知：,2874,1553=*=*那么.________11=*。

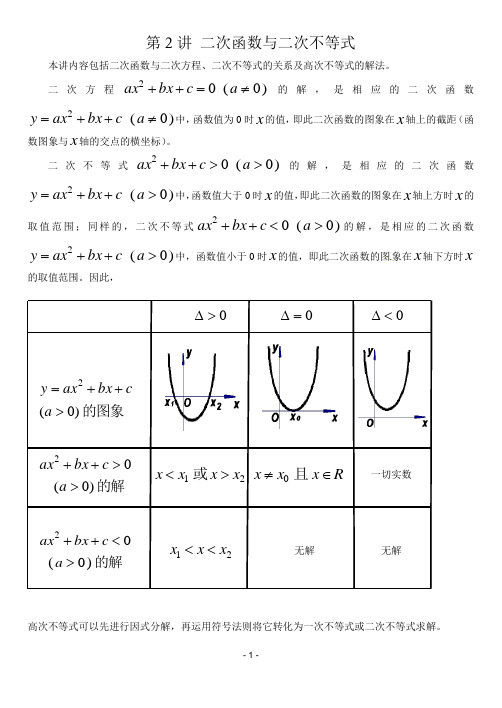
第2讲 二次函数与二次不等式本讲内容包括二次函数与二次方程、二次不等式的关系及高次不等式的解法。

二次方程)0(02≠=++a c bx ax 的解，是相应的二次函数)0(2≠++=a c bx ax y 中，函数值为0时x 的值，即此二次函数的图象在x 轴上的截距（函数图象与x 轴的交点的横坐标）。

二次不等式)0(02>>++a c bx ax 的解，是相应的二次函数)0(2>++=a c bx ax y 中，函数值大于0时x 的值，即此二次函数的图象在x 轴上方时x 的取值范围；同样的，二次不等式)0(02><++a c bx ax 的解，是相应的二次函数)0(2>++=a c bx ax y 中，函数值小于0时x 的值，即此二次函数的图象在x 轴下方时x的取值范围。

因此，0>∆ 0=∆ 0<∆的图象)0(2>++=a c bx ax y的解)0(02>>++a c bx ax21x x x x ><或 R x x x ∈≠且0 一切实数的解)0(02><++a c bx ax21x x x << 无解 无解高次不等式可以先进行因式分解，再运用符号法则将它转化为一次不等式或二次不等式求解。

例1 设二次函数)0(2222<++=a a ax x y 的图象的顶点为A ，与x 轴的交点为C B ,，当ABC ∆为等边三角形时，求a 的值。

例2 当0<a 时，解关于x 的二次不等式（1）05422≥--a ax x ；（2）0)13()1(222<+-++-a a x a x；（3）04)4(22>++-a x a ax。

例3：解高次不等式 （1）;0673<+-x x（2）.0)34)(86(22>+-++x x x x x情景再现 1．抛物线c bx ax y ++=2与x 轴交于B A ,两点，与y 轴交于C 点。

第2讲：二次函数与一元二次方程、不等式(重点题型方法与技巧)目录类型一：一元二次不等式（不含参）的求解 类型二：一元二次不等式（含参）的求解 角度1：两根大小不确定，从两根相等开始讨论角度2：最高项系数含参从0开始讨论 角度3：不可因式分解型，从开始讨论 类型三：一元二次不等式与对应函数、方程的关系类型四：二次不等式恒成立问题 类型五：一元二次函数求最值（含参数）类型六：：根据不等式的解求参数1、四个二次的关系 1.1一元二次函数的零点一般地，对于二次函数2y ax bx c =++，我们把使20ax bx c ++=的实数x 叫做二次函数2y ax bx c =++的零点．1.2次函数与一元二次方程的根、一元二次不等式的解集的对应关系对于一元二次方程20(0)ax bx c a ++=>的两根为12x x 、且12x x ≤，设ac b 42-=∆，它的解按照0>∆，0=∆，0<∆可分三种情况，相应地，二次函数2y ax bx c =++(0)a >的图象与x 轴的位置关系也分为三种情况.因此我们分三种情况来讨论一元二次不等式20ax bx c ++>(0)a >或20ax bx c ++<(0)a >的解集.判别式ac b 42-=∆ 0∆>0∆=0∆<二次函数2y ax bx c =++(0a >的图象一元二次方程20ax bx c ++=(0a >)的根有两个不相等的实数有两个相等的实数根没有实数根根1x ，2x (12x x <)122b x x a==-20ax bx c ++>(0a >)的解集 12{|}x x x x x <>或 {|}2b x x a≠-R20ax bx c ++<(0a >)的解集12{|}x x x x <<∅ ∅2、一元二次不等式的解法1：先看二次项系数是否为正，若为负，则将二次项系数化为正数； 2：写出相应的方程20ax bx c ++=(0)a >，计算判别式∆：①0∆>时，求出两根12x x 、，且12x x <（注意灵活运用十字相乘法）； ②0∆=时，求根ab x x 221-==； ③0∆<时，方程无解 3：根据不等式，写出解集.类型一：一元二次不等式（不含参）的求解典型例题例题1．（2022·全国·高一课时练习）不等式21560x x +->的解集为（ ） A ．{1x x 或1}6x <-B ．116x x ⎧⎫-<<⎨⎬⎩⎭C ．{1x x 或3}x <-D ．{}32x x -<<【答案】B【详解】法一：原不等式即为26510x x --<，即()()6110x x +-<，解得116x -<<，故原不等式的解集为116x x ⎧⎫-<<⎨⎬⎩⎭．法二：当2x =时，不等式不成立，排除A ，C ；当1x =时，不等式不成立，排除D ． 故选：B ．例题2．（2022·陕西省丹凤中学高一期末（理））不等式2280x x +-≤的解集是________． 【答案】{|42}x x -≤≤【详解】解：因为2280x x +-≤，即()()420x x +-≤， 解得42x -≤≤，所以原不等式的解集为{|42}x x -≤≤； 故答案为：{|42}x x -≤≤同类题型演练1．（2022·广东珠海·高一期末）不等式()()130x x ++<的解集是（ ）A ．RB ．∅C ．{31}x x -<<-∣D ．{3xx <-∣，或1}x >- 【答案】C【详解】解：由()()130x x ++<，解得31x -<<-，即不等式的解集为{31}xx -<<-∣； 故选：C2．（2022·四川成都·高一期末（文））不等式()()120x x +->的解集为___________. 【答案】{}|12x x -<<【详解】不等式()()120x x +->可化为()()120x x +-<， 解得：12x -<<.所以原不等式的解集为{}|12x x -<<. 故答案为：{}|12x x -<<类型二：一元二次不等式（含参）的求解 角度1：两根大小不确定，从两根相等开始讨论 典型例题例题1．（2022·全国·高一课时练习）解不等式()2220x c x c -++<.【答案】解：不等式化为()2220x c x c -++<，即()(2)0x c x --<当2>c 时，不等式的解集为{}2x x c <<， 当2c =时，不等式的解集为∅， 当2c <时，不等式的解集为{}2x c x <<例题2．（2022·全国·高三专题练习）求不等式2212x ax a ->（a R ∈）的解集． 【答案】当a>0时，不等式的解集为{|}43a ax x x <->或 当a ＝0时，不等式的解集为{x|x ∈R 且x≠0}； 当a<0时，不等式的解集为{|}34a ax x x <>-或 【详解】试题分析：解含参数的二次不等式，通常要比较其对应方程的两根大小才能写出不等式的解集．本题对应方程两根为13a x =，24ax =-比较这两个根的大小，只需讨论与零的大小关系就可以了．试题解析：原不等式可化为（3x －a ）（4x ＋a ）>0． 当a>0时，不等式的解集为{|}43a a x x x <->或 当a ＝0时，不等式的解集为{x|x ∈R 且x≠0}； 当a<0时，不等式的解集为{|}34a a x x x <>-或 例题3．（2022·广东·高一期末）设函数2()(1)1f x ax a x =-++． (1)当a +∈R 时，求关于x 的不等式()0f x <的解集．【答案】(1)当1a =时，解集为∅；当01a <<时，解集为11x x a ⎧⎫<<⎨⎬⎩⎭；当1a >时，解集为11x x a ⎧⎫<<⎨⎬⎩⎭. ()0f x <，即()2110ax a x -++<，当a +∈R 时，原不等式可化为()110x x a⎛⎫--< ⎪⎝⎭，其解得情况应由1a与1的大小关系确定， 当1a =时，解得x ∈∅； 当1a >时，解得11x a<<； 当01a <<时，解得11x a<<. 综上所述：当1a =时，解集为∅；当01a <<时，解集为11x x a ⎧⎫<<⎨⎬⎩⎭；当1a >时，解集为11x x a ⎧⎫<<⎨⎬⎩⎭. 同类题型演练1．（2022·福建南平·高一期末）当0a <时，求关于x 的不等式2(24)80ax a x +-->的解集． 【答案】2(24)80ax a x +-->，因为0a <，所以不等式可化为2(4)0x x a ⎛⎫+-< ⎪⎝⎭当24a <-时，即102a -<<，原不等式的解集24,a ⎛⎫- ⎪⎝⎭当24a =-时，即12a =-，原不等式的解集为∅当24a >-时即12a <-原不等式的解集2,4a ⎛⎫- ⎪⎝⎭.综上所述，当102a -<<时，原不等式的解24,a ⎛⎫- ⎪⎝⎭；当12a =-时，原不等式的解集为∅；当12a <-时，原不等式的解集2,4a ⎛⎫- ⎪⎝⎭.2．（2022·四川成都·高一期末）设函数()()3y x x a =--，R a ∈. (1)解关于x 的不等式0y <； 【答案】(1)答案见解析.当3a <时，不等式()0f x <的解集为(),3a ， 当3a =时，不等式()0f x <的解集为∅， 当3a >时，不等式()0f x <的解集为()3,a .3．（2022·甘肃省武威第一中学高一开学考试）解关于x 的不等式：()2230x a a x a -++<.【答案】答案见解析【详解】解：()2230x a a x a -++<即()()20x a x a --<， 则对应方程的根为212,==x a x a ，①当0a <或1a >时，原不等式的解集为{}2x a x a <<，②当0a =或1a =时，原不等式的解集为∅，③当01a <<时，原不等式的解集为{}2x a x a <<.角度2：最高项系数含参从0开始讨论典型例题例题1．（2022·湖南·新邵县第二中学高一开学考试）解关于x 的不等式2(1)21(R)ax a x a a a +-+-<-∈.【答案】由题意可得22(1)21(1)10ax a x a a ax a x +-+-<-⇒+--<，当0a =时，不等式可化为1x <，所以不等式的解集为{}1x x <，当0a >时，21(1)10(1)(1)01ax a x ax x x a+--<⇒+-<⇒-<<，当0a <时，2(1)10(1)(1)0ax a x ax x +--<⇒+-<，①当1a =-，解集{}1x x ≠，②当10a -<<，解集为{1x x <或1x a ⎫>-⎬⎭，③当1a <-，解集为{1x x >或1x a ⎫<-⎬⎭.综上所述，当1a <-，不等式的解集为{1x x >或1x a ⎫<-⎬⎭，当1a =-，不等式的解集为{}1x x ≠，当10a -<<，不等式的解集为{1x x <或1x a ⎫>-⎬⎭，当0a =时，不等式的解集为{}1x x <，当0a >时，不等式的解集为11x x a ⎧⎫-<<⎨⎬⎩⎭.例题2．（2022·陕西·西安高新第三中学高一期中）已知函数()2(2)()f x ax a x a =+-∈R .若2a >-，解关于x 的不等式()2f x ≥.【答案】20a -<<时，解集为2|1x x a ⎧⎫≤≤-⎨⎬⎩⎭；0a =时，解集为{}1x x ≤-； 0a >时，解集为2{|x x a≥或1}x ≤- 不等式()2f x ≥，可化为：()2220ax a x +--≥.当0a =时，原不等式即为220x --≥，∴1x ≤-．当0a >时，原不等式化为()210a x x a ⎛⎫-+≥ ⎪⎝⎭，∴2x a ≥或1x ≤-.当20a -<<时，原不等式为()210a x x a ⎛⎫-+≥ ⎪⎝⎭，可化为()210x x a ⎛⎫-+≤ ⎪⎝⎭因21a<-，∴21x a ≤≤-．综上，20a -<<时，原不等式的解集为2|1x x a ⎧⎫≤≤-⎨⎬⎩⎭；0a =时，原不等式的解集为{}1x x ≤-； 0a >时，原不等式的解集为2{|x x a≥或1}x ≤- 同类题型演练1．（2022·全国·高一专题练习）若R a ∈，解关于x 的不等式2(1)10ax a x +++>．【答案】答案见解析.【详解】当0a =时，1x >-，当0a ≠时，1()(1)0a x x a++>，当0a <时，1()(1)0x x a ++<，解得11x a-<<-，当0a >时，1()(1)0x x a++>，若1a =，则1x ≠-，若01a <<，则1x a <-或1x >-，若1a >，则1x <-或1x a>-，所以当0a <时，原不等式的解集是{}|11x x a -<<-；当0a =时，原不等式的解集是{|1}x x >-；当01a <≤时，原不等式的解集是1{|x x a <-或1}x >-；当1a >时，原不等式的解集是{|1x x <-或1}x a>-．2．（2022·福建·莆田一中高一期末）已知函数2()(1)2f x ax a x a =+-+-. 若0a <，解关于x 的不等式()1f x a <-. 【答案】依题意，因0a <，则2()1(1)101()(1)0f x a ax a x x x a<-⇔+-⇔--+><，当1a =-时，11a-=，解得1x ≠， 当10a -<<时，11a ->，解得1x <或1x a>-， 当1a <-时，101a <-<，解得1x a<-或1x >，所以，当1a =-时，原不等式的解集为{R |1}x x ∈≠；当10a -<<时，原不等式的解集为{|1x x <或1}x a>-；当1a <-时，原不等式的解集为1{|x x a<-或1}x >.角度3：不可因式分解型，从开始讨论典型例题例题1．（2022·全国·高一专题练习）解关于x 的不等式：2220()x ax a R ++>∈． 【答案】答案见解析.【详解】关于x 的不等式：2220()x ax a R ++>∈中，∆2242216a a =-⨯⨯=-，当4a >或4a 时，∆0>，对应的一元二次方程有两个实数根2164a a x ---=和2164a a x -+-=，且22161644a a a a ----+-<， 故不等式的解集为216{|4a a x x ---<或216}4a a x -+->；当4a =±时，∆0=，对应的一元二次方程有两个相等的实数根4ax =-，∴不等式的解集为{|}4ax x ≠-；当44a -<<时，∆0<， ∴不等式的解集为R ；综上，4a >或4a时，不等式的解集为216{|4a a x x ---<或216}4a a x -+->；4a =±时，不等式的解集为{|}4ax x ≠-；44a -<<时，不等式的解集为R ．同类题型演练1．（2022·山东滨州·高二期中）已知一元二次函数2()f x x bx c =++，满足(0)2,(1)(1)=-=f f f ．(1)求()f x 的解析式；(2)解关于x 的不等式()2≤f x ax ． 【答案】(1)2()2f x x =+(2)解集见解析(1)解：函数2()f x x bx c =++，由(0)2f =，得2,c = 因为(1)(1)f f -=，所以1212,++=-+b b 解得0b =； 所以2()2f x x =+.(2)关于x 的不等式()2≤f x ax 可化为2220,-+≤x ax 因为248,∆=-a所以当0,∆<即22a -<<时，原不等式对应的方程无实数根， 又二次函数222y x ax =-+的图像开口向上，所以原不等式的解集为∅； 当0∆=，即2a =±时，原不等式对应的方程有两个相等的实数根， 2a =时，原不等式的解集为{}|2=x x ；2a =-时，原不等式的解集为{}|2=-x x ；当0,∆>即2a <-或2a >时，原不等式对应的有两个相等的实数根， 分别为22122,2,=--=+-x a a x a a 且12,x x <所以原不等式解集为{}22|22--≤≤+-x a a a a a .综上所知，当22a -<<时，原不等式的解集为∅； 当2a =时，原不等式的解集为{}|2=x x ； 当2a =-时，原不等式的解集为{}|2=-x x ；当2a <-或2a >时，原不等式解集为{}22|22--≤≤+-x a a a a a .类型三：一元二次不等式与对应函数、方程的关系典型例题例题1．（2022·全国·高一课时练习）已知二次函数2y ax bx c =++的图象如图所示，则不等式20ax bx c ++>的解集是（ ）A ．{}21x x -<<B ．{|2x x <-或1}x >C ．{}21x x -≤≤D ．{|2x x ≤-或1}x ≥【答案】A【详解】由二次函数图象知：20ax bx c ++>有21x -<<. 故选：A例题2．（2022·黑龙江·大庆实验中学高二期末）已知220x kx m -+<的解集为()1,t -（1t >-），则k m +的值为（ ） A ．1- B ．2- C ．1 D ．2【答案】B【详解】解：因为220x kx m -+<的解集为()1,t -（1t >-）， 所以1x =-为220x kx m -+=的根，所以2k m +=-. 故选：B例题3．（2022·黑龙江·大庆中学高二期末）若不等式220ax bx ++>的解集是1123x x ⎧⎫-<<⎨⎬⎩⎭，则0ax b +>的解集为（ ）A ．1,6⎛⎫-∞- ⎪⎝⎭B ．1,6⎛⎫-∞ ⎪⎝⎭C ．1,6⎛⎫-+∞ ⎪⎝⎭D ．1,6⎛⎫+∞ ⎪⎝⎭【答案】A【详解】不等式220ax bx ++>的解集是1123x x ⎧⎫-<<⎨⎬⎩⎭则根据对应方程的韦达定理得到：112311223ba a⎧⎛⎫-+=- ⎪⎪⎪⎝⎭⎨⎛⎫⎪-⋅= ⎪⎪⎝⎭⎩，解得122a b =-⎧⎨=-⎩，则1220x -->的解集为1,6⎛⎫-∞- ⎪⎝⎭故选：A同类题型演练1．（2022·浙江·高三专题练习）已知二次函数2y ax bx c =++的图像如图所示，则不等式20ax bx c ++>的解集是（ ）A ．()2,1-B ．()(),21,-∞-⋃+∞C ．[]2,1-D ．(][),21,-∞-+∞【答案】A【详解】结合图像易知，不等式20ax bx c ++>的解集()2,1-， 故选：A.2．（2022·全国·高一单元测试）若方程()200ax bx c a ++=<有唯一的实数根3，则不等式20ax bx c ++≥的解集为______．【答案】{}3x x =【详解】由已知得抛物线()20y ax bx c a =++<的开口向下，与x 轴交于点()3,0，故不等式20ax bx c ++≥的解集为{}3x x =． 故答案为：{}3x x =3．（2022·江苏·高一）若关于x 的不等式28210mx mx ++<的解集为{}71x x -<<-，则实数m 的值为______. 【答案】3【详解】由题可知，－7和－1是二次方程28210mx mx ++=的两个根， 故()21713m m=-⨯-⇒=.经检验满足题意 故答案为：3.类型四：二次不等式恒成立问题典型例题例题1．（2022·江西吉安·高二期末（文））若关于x 的不等式2220ax ax --<恒成立，则实数a 的取值范围为（ ） A ．[]2,0- B ．(]2,0- C ．()2,0-D ．()(),20,-∞-⋃+∞【答案】B【详解】当0a =时，不等式成立；当0a ≠时，不等式2220ax ax --<恒成立， 等价于()()20,2420,a a a <⎧⎪⎨∆=--⨯-<⎪⎩20a ∴-<<． 综上，实数a 的取值范围为(]2,0-． 故选：B ．例题2．（2022·黑龙江·鸡东县第二中学高二期中）已知命题“[1,2]x ∃∈-，230x x a +>-”是假命题，则实数a 的取值范围是________. 【答案】(,4]-∞-【详解】由题意得，“[1,2]x ∀∈-，230x x a -+≤”是真命题， 则23a x x ≤-+对[1,2]x ∀∈-恒成立，在区间[]1,2-上，23x x -+的最小值为()()21314--+⨯-=-，所以()2min 34a x x ≤-+=-，即a 的取值范围是(,4]-∞-. 故答案为：(,4]-∞-例题3．（2022·全国·高一课时练习）已知关于x 的不等式244x mx x m +>+-． (1)若对任意实数x ，不等式恒成立，求实数m 的取值范围； (2)若对于04m ≤≤，不等式恒成立，求实数x 的取值范围．【答案】(1)(0,4) (2)()()(),00,22,-∞⋃⋃+∞（1）若对任意实数x ，不等式恒成立，即2440x mx x m +--+>恒成立 则关于x 的方程2440x mx x m +--+=的判别式()()24440m m ∆=---+<， 即240m m -<，解得04m <<，所以实数m 的取值范围为(0,4)． （2）不等式244x mx x m +>+-，可看成关于m 的一次不等式()21440m x x x -+-+>，又04m ≤≤，所以224404(1)440x x x x x ⎧-+>⎨-+-+>⎩，解得2x ≠且0x ≠，所以实数x 的取值范围是()()(),00,22,-∞⋃⋃+∞．同类题型演练1．（多选）（2022·全国·高一课时练习）不等式22x bx c x b ++≥+对任意的x ∈R 恒成立，则（ ） A ．2440b c -+≤ B ．0b ≤ C ．1c ≥ D ．0b c +≥【答案】ACD【详解】22x bx c x b ++≥+可整理为()220x b x c b +-+-≥，则()()2224440b c b b c ∆=---=-+≤，故A 正确． 当1b =，2c =时，满足0∆≤，即原不等式成立．B 错误；由0∆≤，得214b c ≥+，所以1c ≥．C 正确；2211042b b b c b ⎛⎫+≥++=+≥ ⎪⎝⎭．D 正确．故选：ACD ．2．（2022·江苏南京·高二期末）2R,10x x x λ∀∈-+>，则λ的取值范围为__________． 【答案】22λ-<<【详解】由题设240λ∆=-<，可得22λ-<<. 故答案为：22λ-<<3．（2022·四川广安·高一期末（理））已知不等式()21460a x x +--<的解集是{}13x x -<<．(1)求常数a 的值；(2)若关于x 的不等式240ax mx ++≥的解集为R ，求m 的取值范围． 【答案】(1)1a =(2)[]4,4-(1)因为不等式()21460a x x +--<的解集是{}13x x -<<．所以－1和3是方程()21460a x x +--=的解，把1x =-代入方程解得1a =．经验证满足题意(2)若关于x 的不等式240ax mx ++≥的解集为R ，即240x mx ++≥的解集为R ， 所以2160m ∆=-≤，解得44m -≤≤，所以m 的取值范围是[]4,4-．4．（2022·四川·盐亭中学高二阶段练习（文））已知函数()()211f x x a x =-++．(1)若关于x 的不等式的()0f x <的解集是{}2x m x <<，求a ，m 的值； (2)设关于x 不等式的()0f x >在[]0,1上恒成立，求实数a 的取值范围． 【答案】(1)32a =，12m =(2)(),1-∞ (1)根据二次不等式的解集与系数的关系可得x m =和2x =是方程()2110x a x -++=的两根，故()221210a -+⨯+=，解得32a =，由韦达定理有21m =，解得12m =. 故32a =，12m = (2)()0f x >在[]0,1上恒成立，即()211x a x +>+恒成立.当0x =时满足题意，当(]0,1x ∈时，min 11x a x ⎛⎫+>+ ⎪⎝⎭恒成立，因为1122x x x x+≥⋅=，当且仅当1x =时取等号.故12a +<，即a的取值范围为(),1-∞.5．（2022·浙江·镇海中学高二期末）已知函数2()4f x x x b =-+，若()0f x <的解集为{}1|x x m <<.(1)求b ，m 的值；(2)当a 为何值时，2()2()10a b x a b x +++-<的解集为R ？ 【答案】(1)3m =，3b = (2)(]4,3--(1)解：由题意可知，240x x b -+<的解集为{}1|x x m <<， 所以1x =与x m =为方程240x x b -+=的两根，141m m b +=⎧∴⎨⋅=⎩，33m b =⎧∴⎨=⎩； (2)解：()()2210a b x a b x +++-<的解集为R ，①当0a b +=时，10-<的解集为R ，30a ∴+=，3a ∴=-；②当0a b +<时，()20Δ4()40a b a b a b +<⎧⎨=+++<⎩，10a b ∴-<+<，130a ∴-<+<，43a ∴-<<-综上所述，a 的取值范围为(]4,3--.类型五：一元二次函数求最值（含参数）典型例题例题1．（2022·全国·高一专题练习）已知函数()222f x x ax =++．(1)当1a =时，求函数()f x 在区间[)23-，上的值域； (2)当1a =-时，求函数()f x 在区间[]1t t +，上的最大值；(3)求()f x 在[]55-，上的最大值与最小值． 【答案】(1)[)1,17(2)221(1)12112t t t t ⎧-+<⎪⎪⎨⎪+≥⎪⎩，，(3)答案见解析（1）当1a =时，()()222211f x x x x =++=++，函数在[)21－，－上单调递减，在()1,3-上单调递增， ()()min 11317x f x f ∴===－，，，∴函数()f x 在区间[)23-，上的值域是[)1,17；（2）当1a =-时，()()222211f x x x x =-+=-+，12t，函数()f x 在区间[]1t t +，上的最大值()()211f t t =-+； 12t ≥，函数()f x 在区间[]1t t +，上的最大值()211f t t +=+； ∴函数()f x 在区间[]1t t +，上的最大值221(1)12112t t t t ⎧-+<⎪⎪⎨⎪+≥⎪⎩，，；（3）函数()()222222f x x ax x a a =++=++- 的对称轴为x a =-，①当5a -<-，即5a >时，函数y 在[]55－，上是增函数， 当5x =-时，函数y 取得最小值为2710a -；当5x =时，函数y 取得最大值为2710a +． ②当50a -≤<，即05a <≤时，当x a =-时，函数y 取得最小值为22-a ；当5x =时，函数y 取得最大值为2710a +．③当05a ≤≤－，即50a ≤≤－时，x =－a 时，函数y 取得最小值为22a －；当5x =－时，函数y 取得最大值为2710a －．④当5a >－，即5a <－时，函数y 在[]55－，上是减函数， 故当5x =－时，函数y 取得最大值为2710a －；当5x =时，函数y 取得最小值为2710a +． 综上，当5a >时，函数的最大值为2710a +，最小值为2710a -，当05a <≤时，函数的最大值为2710a +，最小值为22-a ，当50a ≤≤－时，函数的最大值为2710a －，最小值为22a －，当5a <－时，函数的最大值为2710a －，最小值为2710a + 例题2．（2022·黑龙江·大庆市东风中学高二期末）已知二次函数2()(0)f x ax bx c a =++≠，且满足(0)2f =，(1)()21f x f x x +-=+. (1)求函数()f x 的解析式；(2)当[,2]x t t ∈+（R t ∈）时，求函数()f x 的最小值()g t （用t 表示）． 【答案】(1)2()2f x x =+ (2)222,0()2,2046,2t t g t t t t t ⎧+≥⎪=-<<⎨⎪++≤-⎩（1）因为二次函数2()(0)f x ax bx c a =++≠，且满足(0)2f =，(1)()21f x f x x +-=+， 所以2c =，且22(1)(1)()21a x b x c ax bx c x ++++-++=+，由22(1)(1)()21a x b x c ax bx c x ++++-++=+，得221ax b a x ++=+，所以221a b a =⎧⎨+=⎩，得10a b =⎧⎨=⎩，所以2()2f x x =+.（2）因为2()2f x x =+是图象的对称轴为直线0x =，且开口向上的二次函数， 当0t ≥时，2()2f x x =+在[,2]x t t ∈+上单调递增，则2min ()()2f x f t t ==+；当20t +≤，即2t ≤-时，2()2f x x =+在[,2]x t t ∈+上单调递减，则22min ()(2)(2)246f x f t t t t =+=++=++；当01t t <<+，即20t -<<时，min ()(0)2f x f ==， 综上222,0()2,2046,2t t g t t t t t ⎧+≥⎪=-<<⎨⎪++≤-⎩同类题型演练1．（2021·全国·高一专题练习）已知函数()22f x x mx n =++的图象过点(0,1)-，且满足()()12f f -=．(1)求函数()f x 的解析式；(2)求函数()f x 在[],2a a +上的最小值； 【答案】(1)2()221f x x x =--(2)2min23263,,2331[()],,2221221,.2a a a f x a a a a ⎧++≤-⎪⎪⎪=--<<⎨⎪⎪--≥⎪⎩(1)解：因为函数2()2f x x mx n =++的图象过点(0,1)-， 所以1n =- 又(1)(2)f f -=， 所以1224m -+=-， 解得2m =-，所以2()221f x x x =--；(2)2213()221222f x x x x ⎛⎫=--=-- ⎪⎝⎭，[,2]x a a ∈+，当122a +≤时，即32a ≤-时，函数()f x 在[],2a a +上单调递减，所以2min [()](2)263f x f a a a =+=++，当122a a <<+时，即3122a -<<时，函数()f x 在1,2a ⎡⎤⎢⎥⎣⎦上单调递减，在1,22a ⎡⎤+⎢⎥⎣⎦单调递增，所以min 13[()]22f x f ⎛⎫==- ⎪⎝⎭；当12a ≥时，函数()f x 在[],2a a +上单调递增， 所以2min [()]()221f x f a a a ==--．综上：2min23263,,2331[()],,2221221,.2a a a f x a a a a ⎧++≤-⎪⎪⎪=--<<⎨⎪⎪--≥⎪⎩2．（2021·江西·兴国县将军中学高一期中）已知二次函数()2f x x bx c =++，且()()31f f -=，()00=f ．(1)求函数()f x 的解析式；(2)若函数()()()422g x f x a x =-++，[]1,2x ∈，求函数()g x 的最小值． 【答案】(1)2()2f x x x =+；(2)2min12,0()21,0124,1a a g x a a a a a -≤⎧⎪=--+<<⎨⎪-≥⎩. (1)由(3)(1),(0)0f f f -==，则(0)0f c ==，又931b b -=+，解得2b =， ∴函数()f x 的解析式为2()2f x x x =+.(2)由(1)知，2()2(1)2g x x a x =-++， 其对称轴1x a =+，而[]1,2x ∈， 当11a +≤，即0a ≤时，()g x 在[]1,2上单调递增，min ()(1)12g x g a ==-， 当12a +≥，即1a ≥时，()g x 在[]1,2上单调递减，min ()(2)24g x g a ==-，当01a <<时，2min ()(1)21g x g a a a =+=--+，∴2min12,0()21,0124,1a a g x a a a a a -≤⎧⎪=--+<<⎨⎪-≥⎩. 类型六：：根据不等式的解求参数典型例题例题1．（2021·福建三明·高一期中）已知函数2()2f x ax x c =++，若不等式()0f x <的解集是{|53}x x -<< (1)求()f x 的解析式；(2)若函数()f x 在区间[,2]m m +上的最小值为20，求实数m 的值. 【答案】(1)2()215f x x x =+- (2)－9或5(1)125,3x x =-=是对应方程ax 2＋2x ＋c ＝0的两根.由韦达定理得12122211515x x a ac c x x a ⎧+=-=-⎪=⎧⎪∴⎨⎨=-⎩⎪==-⎪⎩，2()215f x x x ∴=+-；(2)22()215(1)16f x x x x =+-=+-，对称轴为1x =-，当21m +≤-，即3m ≤-时，2min ()(2)(3)16f x f m m =+=+-，由已知得：2(3)1620m +-=， 解得：m ＝3或－9，又3m ≤-，9m ∴=-，当1m ≥-时，2min ()()(1)16f x f m m ==+-，由已知得：2(1)1620m +-=， 解得：m ＝5或－7，又1m ≥-，5m ∴=，当12m m <-<+时，min ()1620f x =-≠，（舍去）， 综上所述，m ＝－9或5.例题2．（2021·河南开封·高一阶段练习）已知函数()221f x x ax =-+，[]1,2x ∈，R a ∈.(1)若()0f x ≤恒成立，求a 的取值范围； (2)若()f x 最小值为4-，求a 的值. 【答案】(1)54a ≥； (2)94. (1)因为2()21f x x ax =-+开口向上，由[]1,2x ∈时，()0f x ≤恒成立，可得()max 0f x ≤，所以(1)0(2)0f f ≤⎧⎨≤⎩，即220540a a -≤⎧⎨-≤⎩，解得：54a ≥，所以a 的取值范围为54a ≥. (2)()221f x x ax =-+对称轴为x a =，开口向上，当1a ≤时，()()min 1224f x f a ==-=-，解得：3a =（舍）；当12a <<时，2min ()()14f x f a a ==-+=-，5a =±（舍）；当2a ≥时，min ()(2)544f x f a ==-=-，94a =； 所以a 的值为94.同类题型演练1．（2022·贵州毕节·高一期末）已知函数2()2(0)f x x ax a =->． (1)当3a =时，解关于x 的不等式5()7f x -<<；(2)函数()y f x =在[],2t t +上的最大值为0，最小值是4-，求实数a 和t 的值． 【答案】(1)(1,1)(5,7)-⋃ (2)0,2t a ==或2,2t a ==(1)当3a =时，不等式5()7f x -<<， 即为2567x x -<-<，即226756⎧-<⎪⎨-<-⎪⎩x x x x ，所以171,5或-<<⎧⎨<>⎩x x x ， 所以11x -<<或57x <<，所以原不等式的解集为(1,1)(5,7)-⋃． (2)(0)(2)0f f a ==，由题意0=t 或22t a +=，这时24a -≤-解得2a ≥， 若0=t ，则2t a +≤，所以()()2242f t f a +==-⇒=；若22t a +=，即22t a a =-≥， 所以()()422f t f a =-=-，则2a =，综上，0,2t a ==或2,2t a ==．2．（2022·全国·高三专题练习（理））已知函数f (x )＝－x 2＋2ax ＋1－a 在x ∈[0，1]时有最大值2，求a的值．【答案】a＝－1或a＝2．【详解】函数f(x)＝－x2＋2ax＋1－a＝－(x－a)2＋a2－a＋1，对称轴方程为x＝a．（1）当a<0时，f(x)max＝f(0)＝1－a，∴1－a＝2，∴a＝－1．（2）当0≤a≤1时，f(x)max＝f(a)＝a2－a＋1，∴a2－a＋1＝2，即a2－a－1＝0，∴a＝125(舍去)．（3）当a>1时，f(x)max＝f(1)＝a，∴a＝2．综上可知，a＝－1或a＝2．。

江苏省金湖县实验中学高中数学 奥赛辅导 初等几何变换（一）基础知识：平面几何证明题历来是各届数学竞赛的热点之一。

1989年中国数学会普委会明确规定：初、高中数学竞赛第二试中各出三道题，其中应有一道平面几何综合证明题。

几何变换是几何内容的核心，大家都知道：作辅助线是初等几何证明的难点，很多情况下，辅助线的作法恰恰是变换的结果。

我们称集合M 到自身的一一对应为一个变换。

初等几何中只讨论平面上的平移、对称、旋转、相似等几种变换。

一、 平移变换1． 定义 设是一条给定的有向线段，T 是平面上的一个变换，它把平面图形F 上任一点X 变到X'，使得=PQ ，则T 叫做沿有向线段PQ 的平移变换。

记为X −−→−)PQ (T X'，图形F −−→−)PQ (T F' 。

2．主要性质 在平移变换下，对应线段平行且相等，直线变为直线，三角形变为三角形，圆变为圆。

两对应点连线段与给定的有向线段平行（共线）且相等。

二、 轴对称变换1． 定义 设l 是一条给定的直线，S 是平面上的一个变换，它把平面图形F 上任一点X变到X'，使得X 与X'关于直线l 对称，则S 叫做以l 为对称轴的轴对称变换。

记为X −→−)l (SX'，图形F −→−)l (SF' 。

2． 主要性质 在轴对称变换下，对应线段相等，对应直线（段）或者平行，或者交于对称轴，且这两条直线的夹角被对称轴平分。

例题：【例1】 P 是平行四边形ABCD 内一点，且∠PAB=∠PCB 。

求证：∠PBA=∠PDA 。

【例2】如图左：线段AA ′,BB ′,CC ′交于点O ，AA'=BB'=CC'=2，∠AOB'=∠BOC'=60°。

求证：Ｓ△AOB'+Ｓ△BOC'+Ｓ△COA'<3【例3】 在两条对角线长度以及夹角一定的所有凸四边形中，试求周长最小的四边形。

二次函数与一元二次方程、不等式【教材分析】三个“二次”即一元二次函数、一元二次方程、一元二次不等式是高中数学的重要内容，具有丰富的内涵和密切的联系，同时也是研究包含二次曲线在内的许多内容的工具高考试题中近一半的试题与这三个“二次”问题有关本节主要是帮助考生理解三者之间的区别及联系，掌握函数、方程及不等式的思想和方法。

【教学目标】课程目标1．通过探索，使学生理解二次函数与一元二次方程，一元二次不等式之间的联系。

2．使学生能够运用二次函数及其图像，性质解决实际问题。

3．渗透数形结合思想，进一步培养学生综合解题能力。

数学学科素养1．数学抽象：一元二次函数与一元二次方程，一元二次不等式之间的联系；2．逻辑推理：一元二次不等式恒成立问题；3．数学运算：解一元二次不等式；4．数据分析：一元二次不等式解决实际问题；5．数学建模：运用数形结合的思想，逐步渗透一元二次函数与一元二次方程，一元二次不等式之间的联系。

【教学重难点】重点：一元二次函数与一元二次方程的关系，利用二次函数图像求一元二次方程的实数根和不等式的解集；难点：一元二次方程根的情况与二次函数图像与x轴位置关系的联系，数形结合思想的运用。

【教学准备】【教学方法】以学生为主体，采用诱思探究式教学，精讲多练。

教学工具：多媒体。

【教学过程】一、情景导入在初中，我们从一次函数的角度看一元一次方程、一元一次不等式，发现了三者之间的内在联系，利用这种联系可以更好地解决相关问题。

类似地，能否从二次函数的观点看一元二次方程和一元二次不等式，进而得到一元二次不等式的求解方法呢？要求：让学生自由发言，教师不做判断。

而是引导学生进一步观察。

研探。

二、预习课本，引入新课阅读课本，思考并完成以下问题1．二次函数与一元二次方程、不等式的解的对应关系。

2．解一元二次不等方的步骤？要求：学生独立完成，以小组为单位，组内可商量，最终选出代表回答问题。

三、新知探究1．一元二次不等式与相应的一元二次函数及一元二次方程的关系如下表：判别式Δ=b2-4acΔ>0Δ=0Δ<0二次函数y=ax2+bx+c（a>0）的图象一元二次方程ax2+bx+c=0（a>0）的根有两相异实根x1，x2（x1<x2）有两相等实根x1=x2没有实数根ax2+bx+c>0（a>0）的解集{x│x>x2或x<x1}{x│x≠‒2b a}Rax2+bx+c<0（a>0）的解集{x│x1<x<x2}∅∅ab2-=22．一元二次不等式ax+bx+c>0（a>0）的求解的算法。

二次函数与方程、不等式基础知识：一、二次函数1． 定义：形如2y ax bx c =++（0a ≠）的函数叫二次函数．2． 二次函数的有关性质① 开口方向00a a >⎧⎨<⎩时，开口向上时，开口向下② 对称轴方程 2b x a=- ③ 定义域RD⎧⎨⎩自然定义域：指定定义域： 3． 图象x =4． 二次函数的解析式 ① 一般式：2y ax bx c =++② 顶点式：2()y a x m n =-+，其中（m ，n ）是二次函数图象的顶点③ 交点式：12()()y a x x x x =--，其中12x x ，是一元二次方程20ax bx c ++=的两实根．二、二次方程1． 当2()f x ax bx c =++中，()0f x =时，即得到二次方程20ax bx c ++=其解的几何意义即为二次函数的图象与x 轴的交点横坐标．2． 根的判别式24b ac ∆=-∆＞0时，方程有两个不相等的实数根； ∆＝0时，方程有两个相等的实数根；∆＜0时，方程无实数根，但有两个共轭的虚数根．3． 根与系数的关系（韦达定理）12b x x a +=-12c x x a= 4． 二次方程根的分布根的位置<=>图象位置<=>等价条件20ax bx c ++=（0a >）若有二根11x >，21x <则(1)0f <若有二根12x x ∈，（2，3） 则(2)0(3)00(23)2f f b a>⎧⎪>⎪⎪∆⎨⎪⎪-∈⎪⎩≥，三、一元二次不等式一元二次不等式20ax bx c ++>（或＜0）的解集，即函数2()f x ax bx c =++的自变量的取值X 围，使其函数值()0f x >（或＜0）的自变量的取值X 围．0∆>0∆=0∆<例题：1． 选择题①2()f x x bxc =++对任意实数t 都有(2)(2)f t f t +=-，那么（ ）A ．(2)(1)(4)f f f <<B ．(1)(2)(4)f f f <<C ．(2)(4)(1)f f f <<D ．(4)(2)(1)f f f <<解：由题意，()f x 的图象关于直线2x =对称，且图象开口向上，画出示意图，由图a象知(2)(1)(4)f f f <<，选A ．② 已知22log (2)a y x x =-在区间（－∞，0）上单调递增，则a 的取值X 围是（ ）A ．1a >B ．11a -<<C ．R a ∈且0a ≠D ．1a <-或1a >解：由函数的单调性的定义知：x 在（－∞，0）上增大时，函数值y 随之增大，故有以下过程：x ： －∞−−−→增大022u x x =-： ＋∞−−→−减小0故必有0＜a 2＜1∴ －1＜a ＜1且a ≠0．选B③ 已知函数y ＝log 21（x 2－6x ＋7），则y （ ）A ．有最大值没有最小值B ．有最小值没有最大值C ．有最大值也有最小值D ．没有最大值也没有最小值 解：∵ u ＝x 2－6x ＋7∈[－2，＋∞） 而定义域要求u ＞0，即u ∈（0，＋∞） ∴ b ＝log 0.5u ∴ b ∈（－∞，＋∞）．选D 2． 填空题①方程22||(R)x x a a -=∈有且仅有两个不同的实数根，则实数a 的取值X 围是_______．解：令212||y x x =-，2y a =则2122(0)2(0)x x x y x x x ⎧-⎪=⎨+<⎪⎩≥，其函数图象如下：思考：a 为何（X②关于x 的方程2290x ax -+=的两个实数根分别为αβ，，则22(1)(1)αβ-+-的最小值是_______________．解：方程有实数根，故24490a ∆=-⨯≥∴3a -≤或3a ≥又29a αβαβ+==，∴ 22(1)(1)y αβ=-+-2()2()22αβαβαβ=+-+-+24416a a =-- ∵ 3a -≤或3a ≥∴ 8y ≥（a ＝3时取等号）∴ min 8y =3． 已知函数24230y x ax a =-++的图象与x 轴无交点，求关于x 的方程3x a +|1|1a =-+的根的X 围． 分析：由于图象与x 轴没有交点，所以0∆<，解得a 的取值X 围又对于每一个a 值，原方程都是一元一次方程，但由于a 是变化的，可知，x 是a 的二次函数，又再转化为二次函数在有限制的区间内的值域问题．解：∵24230y x ax a =-++的图象与x 轴无交点，所以2(4)4(230)0a a ∆=--+< 解得：－2.5＜a ＜3（1）当a ∈（－2.5，1]时，方程化为x ＝（a ＋3）（2－a ）＝－a 2－a ＋6∈（425,49] （2）当a ∈（1，3）时，方程化为x ＝（a ＋3）a ＝a 2＋3a ∈（4，18）综上所述：x ∈（49，18）4． 设a ，b 为实常数，k 取任意实数时，函数y ＝（k 2＋k ＋1）x 2－2（a ＋k ）2x ＋（k 2＋3ak ＋b ）的图象与x 轴都交于点A （1，0）．① 求a 、b 的值；② 若函数与x 轴的另一个交点为B ，当k 变化时，求|AB |的最大值．分析：由A 在曲线上，得k 的多项式对k 恒成立，即可求的a ，b 的值．解：⑴由已知条件，点A （1，0）在函数图象上，故（k 2＋k ＋1）－2（a ＋k ）2＋（k 2＋3ak ＋b ）＝0整理得：（1－a ）k ＋（b ＋1－2a 2）＝0∵ 对k ∈R ，上式恒成立∴ 1－a ＝0且b ＋1－2a 2＝0从而a ＝1，b ＝1y ＝（k 2＋k ＋1）x 2－2（k ＋1）2x ＋（k 2＋3k ＋1）⑵设B （α，0），则|AB |＝|α－1|∵（k 2＋k ＋1）x 2－2（k ＋1）2x ＋（k 2＋3k ＋1）＝0的两个根为1、α，由韦达定理1•α＝22311k k k k ++++ 整理得：2(1)(3)(1)0k k ααα-+-+-=α＝1时，得2k ＝0 ⇒k ＝0 α≠1时，∵ k ∈R ，∴ 0∆≥即2(3)4(1)0αα---≥ 得：513α-≤≤且1α≠ 综合得：513α-≤≤ ∴ 2213α--≤≤ ∴ |AB |＝|α－1|∈[0，2] 即|AB |的最大值为2．5． 设实数a 、b 、c 满足a 2－bc －8a ＋7＝0 …………①b 2＋c 2＋bc －6a ＋6＝0 …………②求a 的取值X 围．分析：如何将含有三个变量的两个方程组成的方程组问题，转化为只含有a 的不等式，是解决本题的关键，仔细分析观察方程组的特点，发现可以利用a 来表示bc 及b ＋c ，从而用韦达定理构造出a 为变量的一元二次方程，由0∆≥建立a 的不等式．解：由①得：bc ＝a 2－8a ＋7 …………③由①②得：（b ＋c ）2＝a 2－2a ＋1即b ＋c ＝±（a －1） …………④由③④得b ，c 为方程x 2±（a －1）x ＋（a 2－8a ＋7）＝0的两个实数根，由于b ，c ∈R，所以0∆≥即：[±（a －1）]2－4（a 2－8a ＋7）≥0即：a 2－10a ＋9≤0得：1≤a ≤96． 设二次函数2()f x ax bx c =++（a ＞0），方程()0f x x -=的两个根12x x ，满足1210x x a<<<． I ．当x ∈（0，1x ）时，证明x ＜()f x ＜1x ；Ⅱ．设函数()f x 的图象关于直线0x x =对称，证明：102x x <． 分析：由于涉及方程根的问题，故需用韦达定理来分析和解决．证明： I ．令F （x ）＝f （x ）－x ．因为x 1、x 2是方程f （x ）－x ＝0的根，得F （x ）＝a （x －x 1）（x －x 2）当x ∈（0，x 1）时，由于x 1＜x 2，x －x 1＜0，x －x 2＜0得（x －x 1）（x －x 2）＞0，又a ＞0，得F （x ）＝a （x －x 1）（x －x 2）＞0即x ＜f （x ）．而x 1－f （x ）＝x 1－[x －F （x ）]＝x 1－x ＋a （x －x 1）（x －x 2）＝（x 1－x ）[1－a （x －x 2）]因为0＜x ＜x 1＜x 2＜1a所以x 1－x ＞0， 1－a （x －x 2）＞1－a ·1a＞0 得 x 1－f （x ）＞0即 f （x ）＜x 1． Ⅱ．依题意知x 0＝－2b a． 因为x 1，x 2是方程f （x ）－x ＝0的根，即x 1，x 2是方程ax 2＋（b －1）x ＋c ＝0的根，所以 x 1＋x 2＝－1b a -x 0＝－1212()11222a x x ax ax b a a a+-+-==因为21ax <，所以0x <1122ax x a =． 7． 若关于x 的二次方程7x 2－（p ＋13）x ＋p 2－p －2＝0的两根αβ，满足0＜α＜1＜β＜2，某某数p 的取值X 围．解：设f （x ）＝7x 2－（p ＋13）x ＋p 2－p －2根据题意得：(0)0(1)0(2)0f f f >⎧⎪<⎨⎪>⎩即 2222028030p p p p p p ⎧-->⎪--<⎨⎪->⎩解得：p ∈（－2，－1）∪（3，4）．。