动量定理验证

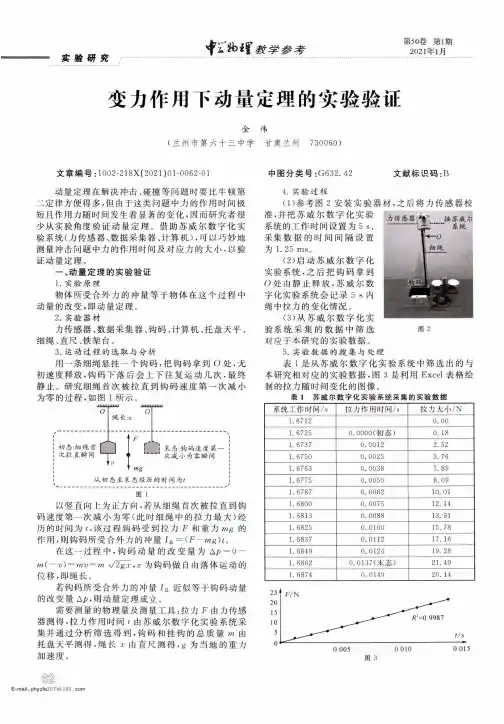
实验研究教•学参考第50卷第1期2021年1月变力作用下动量定理的实验验证金伟(兰州市第六十三中学甘肃兰州 730060)文章编号：l〇〇2-218X ( 2021)01-0062-01动量定理在解决冲击、碰撞等问题时要比牛顿第 二定律方便得多，但由于这类问题中力的作用时间极 短且作用力随时间发生着显著的变化，因而研究者很 少从实验角度验证动量定理。

借助苏威尔数字化实 验系统（力传感器、数据采集器、计算机），可以巧妙地 测量冲击问题中力的作用时间及对应力的大小，以验 证动量定理。

一、动量定理的实验验证1. 实验原理物体所受合外力的冲量等于物体在这个过程中 动量的改变，即动量定理。

2. 实验器材力传感器、数据采集器、钩码、计算机、托盘天平、 细绳、直尺、铁架台。

3. 运动过程的选取与分析用一条细绳悬挂一个钩码，把钩码拿到〇处，无初速度释放，钩码下落后会上下往复运动几次，最终静止。

研究细绳首次被拉直到钩码速度第一次减小为零的过程，如图1所示。

/////////"/，/////////////初态:细绳首次拉直瞬间<,F人…卜末态:钩码速度第一►次减小为零瞬间m g从初态至末态经历的时间为/图1以竖直向上为正方向，若从细绳首次被拉直到钩 码速度第一次减小为零（此时细绳中的拉力最大）经 历的时间为f，该过程钩码受到拉力F 和重力m g 的 作用，则钩码所受合外力的冲量=在这一过程中，钩码动量的改变量为Ap = 0 —m i — v ') = m v =m为钩码做自由落体运动的位移，即绳长。

若钩码所受合外力的冲量近似等于钩码动量 的改变量A /)，则动量定理成立。

需要测量的物理量及测量工具:拉力F 由力传感 器测得，拉力作用时间？由苏威尔数字化实验系统采 集并通过分析筛选得到.钩码和挂钩的总质量w 由 托盘天平测得，绳长i 由直尺测得，g 为当地的重力 加速度。

中图分类号：G 632.42 文献标识码：B4. 实验过程(1) 参考图2安装实验器材，之后将力传感器校 准，并把苏威尔数字化实验 系统的工作时间设置为5 s、采集数据的时间间隔设置 为 1. 25 m s 。

用光电门验证动量定理
要使用光电门验证动量定理，可以按照以下步骤进行：
1. 准备材料和设备：光电门、光源、平台、小球等。

2. 将光电门放置在平台上，并确保其能够正常工作。

3. 选取一颗小球放在光电门的发光面前，确保小球与光电门之间有一段适当的距离。

4. 设置光源并将光源对准光电门的接收器，确保光能能够准确地被感应到。

5. 记录小球在被光能照射之前和照射之后通过光电门的时间。

6. 根据光电门的测量结果计算小球通过光电门时的速度和动量。

7. 使用动量定理，将小球在照射前后的动量进行比较，并验证动量定理是否成立。

在实验过程中，需要注意以下事项：
- 确保光电门的位置和实验环境的稳定性，以减少误差。

- 精确测量小球通过光电门的时间，并注意记录结果。

- 确保小球没有被其他力或因素干扰，以保持实验的准确性。

- 在进行实验前，可以先进行一些预实验，以确定实验方法和
参数的准确性。

动量定理及其应用动量定理是物理学中的重要概念之一，它描述了物体运动的性质和变化。

本文将介绍动量定理的基本原理、公式推导以及其在实际应用中的意义和重要性。

一、动量定理的基本原理动量定理是由牛顿提出的，它描述了质点的运动状态和所受外力之间的关系。

根据动量定理的表述，一个质点的动量的变化量等于作用于质点的力的时间积分。

换句话说，当一个物体受到外力作用时，它的动量会发生改变。

动量定理可以表述为以下公式：F = Δp/Δt其中，F代表物体所受的力，Δp为物体的动量变化量，Δt为时间的变化量。

该公式表示力等于物体动量的变化率。

二、动量定理的公式推导动量是物体的运动状态的衡量，它的大小与物体的质量和速度有关。

根据定义，动量p等于物体质量m与速度v的乘积：p = m * v。

当一个物体受到外力F作用时，根据牛顿第二定律F = ma（a为物体的加速度），可得：F = m * a根据运动学公式v = u + at（u为初速度，t为时间），可以将加速度a表示为：a = (v - u) / t将上述两个公式代入牛顿第二定律中得：F = m * (v - u) / t进一步整理可以得到：F * t = m * (v - u)F * t = m * Δv根据动量的定义p = m * v，将上述公式代入可得：F * t = Δp经过推导，我们得到了动量定理的基本公式F = Δp/Δt。

三、动量定理的应用动量定理在物理学和工程学中有着广泛的应用，以下是一些常见的应用场景：1. 交通事故分析：动量定理可以帮助我们分析交通事故中车辆的碰撞情况，准确计算撞击力的大小以及车辆运动状态的变化。

2. 火箭推进原理：在航天工程中，动量定理被用来解释火箭如何通过燃料的喷射产生反作用力，从而达到推进的效果。

3. 球类运动：动量定理可以解释球类运动中击球和接球的力学过程。

例如，乒乓球运动中击球员可以通过控制球的反冲力使得球的速度和方向发生改变。

4. 器械运动分析：动量定理可以用来解析各种器械运动的特点和规律，例如击球运动、举重等。

动量定理的推导与碰撞问题分析动量定理是物理学中的重要定律，描述了物体在受到外力作用下的运动状态变化。

本文将对动量定理的推导进行阐述，并分析碰撞问题。

一、动量定理的推导动量定理可以通过牛顿第二定律和运动学关系来推导得到。

先回顾一下相关的基本概念：1. 动量（Momentum）：物体的动量等于它的质量与速度的乘积，用数学表示为p=mv，其中p表示动量，m表示质量，v表示速度。

2. 牛顿第二定律：物体的加速度与作用在物体上的总力成正比，反比于物体的质量。

数学表达式为F=ma，其中F表示力，m表示质量，a表示加速度。

根据牛顿第二定律，可以得到物体的加速度与作用在物体上的力的关系为a=F/m。

同时，根据运动学关系v=u+at，其中v表示末速度，u表示初速度，a表示加速度，t表示时间。

将上述两个公式结合起来，可以得到动量定理的推导过程：设物体初速度为u，末速度为v，时间为t。

根据运动学关系可得v=u+at，进一步可推导出a=(v-u)/t。

代入牛顿第二定律的公式F=ma中的加速度a，可以得到F=m(v-u)/t。

根据动量的定义p=mv，可以推导出物体的初动量p₁=mu，末动量p₂=mv。

根据动量的变化Δp=p₂-p₁可得，Δp=mv-mu=m(v-u)。

而Δp表示物体动量的改变量，根据动量定理，动量的改变量等于作用在物体上的力的大小乘以时间，即Δp=Ft。

将前面得到的Δp的表达式代入，可以得到Ft=m(v-u)。

而右边的表达式m(v-u)即为动量的变化量。

因此，根据上述推导过程，可以得出动量定理的数学表达式为：Ft=Δp=m(v-u)。

二、碰撞问题的分析碰撞是物体之间相互作用的一种形式，可以分为完全弹性碰撞和完全非弹性碰撞两种情况。

下面将对这两种碰撞情况进行分析。

1. 完全弹性碰撞完全弹性碰撞是指碰撞之后物体之间没有能量损失，且动量守恒。

在完全弹性碰撞中，物体的速度改变方向，但总动能不变。

根据动量守恒可以得到，对于完全弹性碰撞，碰撞前物体的总动量等于碰撞后物体的总动量。

动量定理解析一、引言动量是物体运动的基本性质之一，描述了物体的运动状态以及与其他物体相互作用的程度。

动量定理是物理学中的基本定律之一，揭示了力对物体运动状态的影响。

本文将对动量定理进行深入分析和解析。

二、动量的定义和性质动量是一个物体的质量与速度的乘积，用数学式表示为p=mv，其中p为动量，m为质量，v为速度。

从定义中可以看出，质量越大，速度越快的物体具有更大的动量。

动量是一个矢量量，即具有大小和方向，与速度的方向一致。

若物体的速度发生改变，其动量也会相应改变。

三、动量定理的表述动量定理是指一个力在作用于物体上时，会引起物体动量的变化。

根据牛顿第二定律F=ma，将加速度a用速度v和时间t表示，即a=(v-u)/t，其中u为物体作用力前的速度。

代入动量的定义式p=mv和速度变化的关系式v-u=at，可以得到动量定理的数学表达式为FΔt=Δmv，即力乘以时间等于动量的改变量。

根据动量定理的数学表达式，我们可以得到以下几个重要结论：1. 力和时间的乘积引起的动量变化是一个矢量量，其方向与力向量相同，大小等于力的大小乘以时间。

2. 若力和时间的乘积为正，即力和物体的运动方向相同，那么物体的动量会增加；若力和时间的乘积为负，即力和物体的运动方向相反，那么物体的动量会减小。

3. 动量定理不仅适用于单个物体的运动，也适用于多个物体同时作用的情况。

在多体系统中，要考虑各个物体之间的相互作用力。

四、动量定理的应用1. 运动中的汽车在汽车行驶过程中，动量定理可以解释为何汽车的速度与质量成反比。

考虑两辆质量相同的汽车，当相同大小的力作用于两辆汽车上时，质量较大的汽车受到的加速度较小，因此速度改变较小，而质量较小的汽车则受到较大的加速度，速度改变较大。

这说明了质量越大的物体，受到相同作用力产生的速度改变越小。

2. 球类运动在球类运动中，动量定理可以解释为何把一个球踢或投得越快，球的反弹或射程越远。

由于力和时间的乘积等于动量的改变量，对于一个静止的球而言，施加给球的力越大，作用时间越长，动量改变量越大，球的速度越快，它的运动轨迹也会更远。

实验八验证动量守恒定律注意事项1．前提条件：碰撞的两物体应保证“水平”和“正碰”。

2．方案提醒(1)若利用气垫导轨进行验证，调整气垫导轨时，应注意利用水平仪确保导轨水平。

(2)若利用两小车相碰进行验证，要注意平衡摩擦力。

(3)若利用平抛运动规律进行验证①斜槽末端的切线必须水平；②入射小球每次都必须从斜槽同一高度由静止释放；③选质量较大的小球作为入射小球；④实验过程中实验桌、斜槽、记录的白纸的位置要始终保持不变。

命题点一 教材原型实验【例1 (2021·四川攀枝花市统考)某学习小组用如图2所示的实验装置探究碰撞中的不变量。

将打点计时器固定在光滑水平桌面的一端，把纸带穿过打点计时器，连在小车A 的后面。

让小车A 运动，小车B 静止。

在两小车的碰撞端分别装上撞针和橡皮泥，碰撞时撞针插入橡皮泥中，把两小车连成一体。

某次实验中使用的两车质量均为0.6 kg ，与打点计时器连接的交流电频率为50 Hz ，得到的纸带如图3所示。

图2图3请回答下列问题：(1)纸带的________(选填“a ”或“b ”)端与小车A 相连。

(2)碰撞前系统的总动量为______kg·m/s ，碰撞后系统的总动量为______kg·m/s(保留2位有效数字)。

答案 (1)b (2)0.56 0.54解析 (1)从所给的纸带来看，a 端的点迹较密，b 端较疏，b 端速度大，说明b 端是碰撞前打出的点迹，故b 端跟小车相连。

(2)碰撞前的速度可以用靠近b 端的三段的平均速度表示，v 0＝（12.60－7.00）×10－23×0.02m/s ＝0.93 m/s 所以碰撞前的总动量p ＝m A v 0＝0.6×0.93 kg·m/s ＝0.56 kg·m/s碰撞后的速度用靠近a 端的五段表示v ＝（4.60－0.10）×10－25×0.02m/s ＝0.45 m/s所以碰撞后的总动量p′＝(m A＋m B)v＝1.2×0.45 kg·m/s＝0.54 kg·m/s。

验证动量守恒定律一、实验目的验证一维碰撞中的动量守恒。

二、实验原理在一维碰撞中,测出物体的质量m 1、m 2和碰撞前后物体的速率v 、v',找出碰撞前的动量p=m 1v 1+m 2v 2及碰撞后的动量p'=m 1v 1'+m 2v 2',看碰撞前后动量是否守恒。

三、实验器材方案一:斜槽,大小相等、质量不同的小钢球两个,重垂线一条,白纸,复写纸,天平一台,刻度尺,圆规。

方案二:光滑长木板、打点计时器、纸带、小车(两个)、天平、撞针、橡皮泥、刻度尺。

方案三:气垫导轨、光电计时器、天平、滑块(两个)、重物、弹簧片、细绳、弹性碰撞架、胶布、撞针、橡皮泥。

方案四:带细线的小球(两套)、铁架台、天平、量角器、坐标纸、胶布等。

四、实验步骤与数据处理方案一 方案二 方案三 方案四 利用等大小球做平抛运动完成一维碰撞 在粗糙斜面上两车碰撞完成一维碰撞利用气垫导轨完成一维碰撞 利用等长悬线悬挂等大小球完成一维碰撞根据平抛测速度x hgxv ∝=2 纸带测速度光电门测速度 机械能守恒测速度gh v 2= m 1·OP ＝m 1·OM ＋m 2·ONm 1·v 0＝（m 1＋m 2）v 1m 1·v 0=m 1·v 1＋m 2·v 2m 1·v 0＝m 1·v 1＋m 2·v 2(1)碰撞的两物体应保证“水平”和“正碰”。

(2)选质量较大的小球作为入射小球，即m 入＞m 被碰。

六、误差分析(1)测量误差 (2)阻力 创新角度 实验装置图创新解读如图，用“碰撞实验器”可以验证动量守恒定律，即研究两个小球在轨道水平部分碰撞前后的动量关系。

(1)实验中，直接测定小球碰撞前后的速度是不容易的，但是，可以通过仅测量________(填选项前的符号)，间接地解决这个问题。

A．小球开始释放高度hB．小球抛出点距地面的高度HC．小球做平抛运动的射程(2)图中O点是小球抛出点在地面上的垂直投影。

动量定理及其推导动量定理是物理学中重要的基本定理之一，它描述了物体受力作用下的运动状态变化。

本文将介绍动量定理的基本概念、推导过程以及其在物理学中的应用。

一、动量定理的基本概念动量是描述物体运动状态的物理量，它是物体质量与速度的乘积。

动量定理描述了物体受力作用下的动量变化情况。

根据动量定理，当物体受到外力作用时，它的动量将发生变化。

二、动量定理的推导过程动量定理可以通过牛顿第二定律来推导。

牛顿第二定律描述了物体受力作用下的加速度变化，可以表示为F=ma，其中F为物体所受合力，m为物体的质量，a为物体的加速度。

对于物体的动量，定义为p=mv，其中p为动量，m为物体质量，v为物体速度。

根据这个定义，物体动量的变化可以表示为Δp=mΔv。

考虑一个时间间隔Δt内，物体由初速度v1变化到末速度v2，那么Δv=v2-v1。

通过牛顿第二定律和动量定义，可以得到以下推导过程：F=ma （牛顿第二定律）=F(mΔv/Δt) （将Δv代入）=F(Δp/Δt) （将Δp=mΔv代入）=Fdp/dt （取极限，即Δt趋近于0）所以，根据推导，动量定理可以表达为Fdp/dt。

三、动量定理的应用动量定理在物理学中有广泛的应用。

以下简要介绍几个常见的应用场景。

1. 弹性碰撞在弹性碰撞中，物体之间发生碰撞，初速度和末速度发生变化。

根据动量守恒定律和动量定理，可以分析碰撞后物体的末速度。

通过使用动量定理，可以推导出碰撞过程中物体的运动方向和速度。

2. 爆炸运动在爆炸过程中，物体受到内部产生的巨大力量的作用，动量定理可用来分析爆炸物运动的特性。

通过分析物体受到的作用力和动量变化，可以研究爆炸的冲击效应和能量释放情况。

3. 水平投掷运动在水平投掷运动中，物体在竖直方向上受到重力作用，而在水平方向上匀速运动。

通过应用动量定理，可以分析物体在水平方向上的动量变化和受力情况，从而得出运动的轨迹和最终速度。

4. 动量守恒动量定理与动量守恒定律密切相关。

验证动量定理(恒力)实验原理
动量定理（恒力）实验原理的验证方法如下：
1. 准备一条直线轨道和一个小推车。

轨道应保证平整且无摩擦，可用地板或桌面作为轨道。

2. 将推车放在轨道上，确保推车能够自由移动，并且不受到任何其他力的影响，如重力或摩擦力。

3. 测量推车的质量m，并记录下来。

4. 用一个弹簧测力计将推车推出一段距离，并记录下弹簧测力计的示数F。

5. 用一个计时器测量推车从静止状态到达一定速度时的时间t，并记录下来。

6. 根据推车的质量m、推车的初速度为0、推车的末速度v以
及时间t，计算推车的动量。

7. 根据弹簧测力计的示数F和推车所受力的方向，计算推车
所受的恒力。

8. 比较推车的动量与推车所受力的产品，如果它们的值接近或相等，就证实了动量定理（恒力）。

需要注意的是，在实验中应尽量减小其他干扰因素对推车运动
的影响，例如地面的不平整、空气阻力等。

实验过程中的误差也需要进行控制和记录，以保证实验结果的准确性。

《动量定理》动量定理，实验验证在物理学的广袤领域中，动量定理是一个具有重要意义的基本原理。

它不仅在理论上为我们理解物体的运动和相互作用提供了深刻的洞察，而且在实际应用中也发挥着关键作用。

那么，什么是动量定理？又如何通过实验来验证它呢？动量定理指出，合外力的冲量等于物体动量的增量。

用公式表达即为：＄I ＝＼Delta p$，其中$I$表示合外力的冲量，＄＼Delta p$表示动量的增量。

为了更直观地理解动量定理，让我们先来看一个简单的例子。

假设一个质量为$m$的小球，以初速度$v_1$在光滑水平面上运动。

如果在一段时间$t$内，小球受到一个恒定的水平外力$F$的作用，速度变为$v_2$。

根据动量的定义，小球的初动量$p_1 ＝ mv_1$，末动量$p_2 ＝mv_2$，动量的增量$＼Delta p ＝ p_2 p_1 ＝ m(v_2 v_1)＄。

而合外力的冲量$I ＝ F ＼times t$。

由于动量定理成立，所以有$F ＼times t ＝ m(v_2 v_1)＄。

接下来，我们通过一个具体的实验来验证动量定理。

实验装置包括一个气垫导轨、一个滑块、两个光电门、一个气源、一个数字计时器以及一个力传感器。

首先，将气垫导轨调至水平状态，打开气源，使滑块能在导轨上近似无摩擦地运动。

在滑块上安装一个遮光片，让滑块通过两个相距一定距离的光电门。

数字计时器可以记录滑块通过每个光电门的时间，从而计算出滑块通过两个光电门的速度。

将力传感器固定在滑块的一端，通过施加一个已知大小和方向的外力，记录外力的大小和作用时间。

实验开始时，让滑块以一定的初速度通过第一个光电门，记录此时的速度$v_1$和对应的时间$t_1$。

然后，施加外力，让滑块通过第二个光电门，记录速度$v_2$和时间$t_2$。

根据实验数据，计算出滑块的初动量$p_1 ＝ m v_1$，末动量$p_2＝ m v_2$，动量的增量$＼Delta p ＝ p_2 p_1$。

《科学验证：动量守恒定律》讲义一、动量守恒定律的基本概念在物理学中，动量守恒定律是一个极其重要的基本定律。

那什么是动量呢？动量可以简单地理解为物体运动的“冲量”。

它等于物体的质量乘以其速度。

用公式表示就是：p ＝ mv，其中 p 是动量，m 是物体的质量，v 是物体的速度。

而动量守恒定律说的是，如果一个系统不受外力或者所受外力的矢量和为零，那么这个系统的总动量保持不变。

想象一下，在一个没有摩擦力和其他外力干扰的理想环境中，两个物体相互碰撞。

碰撞前，它们各自有着一定的动量；碰撞后，虽然它们的速度可能发生了变化，但整个系统的总动量是不变的。

二、动量守恒定律的推导为了更深入地理解动量守恒定律，我们来进行一下简单的推导。

假设一个系统中有两个物体，质量分别为 m1 和 m2，速度分别为v1 和 v2 。

它们相互作用，经过一段时间后，速度分别变为 v1' 和 v2' 。

根据牛顿第二定律，物体所受的合力等于其动量的变化率。

对于物体 1 ，有：F1 ＝ dp1/dt ＝ m1 （v1' v1) ／ t ；对于物体 2 ，有：F2 ＝dp2/dt ＝ m2 （v2' v2) ／ t 。

因为系统所受外力的矢量和为零，所以 F1 ＋ F2 ＝ 0 ，即：m1（v1' v1) ／ t ＋ m2 （v2' v2) ／ t ＝ 0 。

整理可得：m1 v1 ＋ m2 v2 ＝ m1 v1' ＋ m2 v2' 。

这就证明了在这个系统中，碰撞前后的总动量是守恒的。

三、动量守恒定律的条件前面提到，动量守恒定律成立的条件是系统不受外力或者所受外力的矢量和为零。

但在实际情况中，完全不受外力的情况是很少见的。

然而，在很多情况下，我们可以近似地认为系统的动量守恒。

比如，在碰撞过程中，如果相互作用的时间非常短，而外力的作用又相对很小，那么我们就可以忽略外力的影响，认为系统的动量守恒。

動量定理物體運動的量化描述动量定理是物体运动的量化描述。

根据动量定理，物体的动量变化与作用力的大小和作用时间的乘积成正比。

动量，是描述物体运动状态的物理量，一般用字母p表示。

它的大小等于物体的质量m与速度v的乘积，即p = mv。

动量定理的数学表达式为：FΔt = Δp，其中F表示作用力，Δt表示作用时间，Δp表示动量变化。

根据这个公式，当物体受到一个作用力时，它的动量就会发生改变。

动量定理可以用来解释物体的加速过程。

当物体受到一个恒定的力作用时，根据牛顿第二定律F = ma，可以推导出物体的加速度a与作用力F的关系为a = F/m。

结合动量定理，可以得出动量随时间的变化关系Δp/Δt = ma，即动量变化率等于物体的加速度。

动量定理还可以解释碰撞过程。

在碰撞中，物体间会相互作用力，并且在瞬间发生相互作用时间Δt内的动量变化。

根据动量定理，可以计算碰撞后物体的速度变化。

动量定理的应用范围广泛。

在工程中，人们可以利用动量定理来设计安全气囊、防护装置等，以减小碰撞造成的伤害。

在交通运输中，动量定理也被广泛应用于车辆碰撞安全的研究。

此外，动量定理还被用于解释天体运动及宇宙起源等领域的研究。

总结起来，动量定理是描述物体运动的重要定律，能够定量地描述物体的运动状态及其变化。

通过运用动量定理，可以更好地理解物体的加速过程和碰撞过程，提高人们对物体运动的认识和应用。