下载文档原格式
玻尔的原子理论——三条假设（1）“定态假设”：原子只能处于一系列不连续的能量状态中，在这些状态中，电子虽做变速运动，但并不向外辐射电磁波，这样的相对稳定的状态称为定态。
定态假设实际上只是给经典的电磁理论限制了适用范围：原子中电子绕核转动处于定态时不受该理论的制约。
（2）“跃迁假设”：电子绕核转动处于定态时不辐射电磁波，但电子在两个不同定态间发生跃迁时，却要辐射（吸收）电磁波（光子），其频率由两个定态的能量差值决定hv=E 2-E 1。
跃迁假设对发光（吸光）从微观（原子等级）上给出了解释。
（3）“轨道量子化假设”：由于能量状态的不连续，因此电子绕核转动的轨道半径也不能任意取值，必须满足)3,2,1(2 ==n nh mvr π。
轨道量子化假设把量子观念引入原子理论，这是玻尔的原子理论之所以成功的根本原因。
[P 4.] 二、氢原子能级及氢光谱 （1）氢原子能级: 原子各个定态对应的能量是不连续的，这些能量值叫做能级。
①能级公式：)6.13(1112eV E E n E n -==； ②半径公式：)m .r (r n r n 1011210530-⨯==。
（2）氢原子的能级图 （3）氢光谱在氢光谱中，n=2,3,4,5,……向n=1跃迁发光形成赖曼线系；n=3,4,5,6向n=2跃迁发光形成巴耳末线系；n=4,5,6,7……向n=3跃迁发光形成帕邢线系；n=5,6,7,8……向n=4跃迁发光形成布喇开线系，其中只有巴耳末线系的前4条谱线落在可见光区域内。
[P5 .]三、几个重要的关系式（1）能级公式 2126131neV .E n E n -== （2）跃迁公式 12E E h -=γ（3）半径公式 )m .r (r n r n 1011210530-⨯== （4） 动能跟n 的关系由 n n n r mv r ke 222= 得 2221221n r ke mv E n n kn ∝== （5）速度跟n 的关系n r m r ke v nn n 112∝== （6）周期跟n 的关系332n r v r T n nn n ∝==πn E /eV ∞ 0 4。
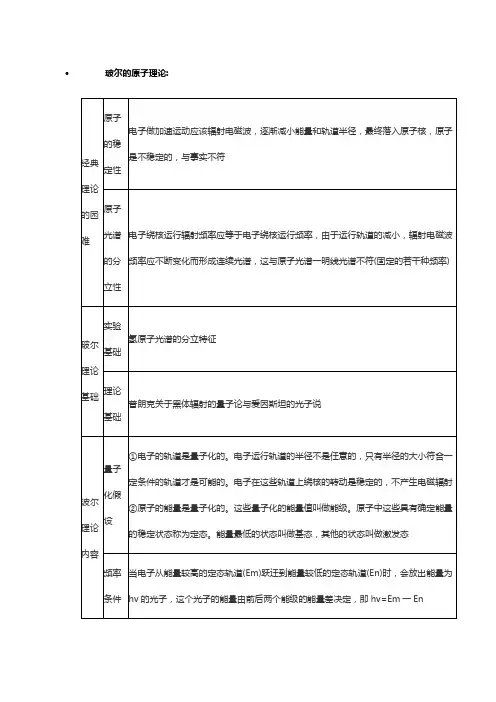
玻尔的原子理论:∙玻尔的原子理论的成功与局限:∙玻尔的原子理论第一次将量子观引入原子领域，提出定态和跃迁的概念，成功地解释了氢原子光谱规律，但玻尔引入的量子化观点并不完善。
在量子力学中，核外电子并没有确定的轨道，玻尔的电子轨道只不过是电子出现概率较大的地方。
把电子的概率分布用图像表示时，用小黑点的稠密程度代表概率的大小，其结果如同电子在原子核周围形成的云雾，称为“电子云∙氢原子的能级:1、氢原子的能级图2、光子的发射和吸收①原子处于基态时最稳定，处于较高能级时会自发地向低能级跃迁，经过一次或几次跃迁到达基态，跃迁时以光子的形式放出能量。
②原子在始末两个能级E m和E n（m>n）间跃迁时发射光子的频率为ν，其大小可由下式决定：hυ=E m-E n。
③如果原子吸收一定频率的光子，原子得到能量后则从低能级向高能级跃迁。
④原子处于第n能级时，可能观测到的不同波长种类N为：。
⑤原子的能量包括电子的动能和电势能（电势能为电子和原子共有）即：原子的能量E n=E Kn+E Pn。
轨道越低，电子的动能越大，但势能更小，原子的能量变小。
电子的动能：，r越小，E K越大。
氢原子的能级及相关物理量:在氢原子中，电子围绕原子核运动，如将电子的运动看做轨道半径为r的圆周运动，则原子核与电子之间的库仑力提供电子做匀速圆周运动所需的向心力，那么由库仑定律和牛顿第二定律，有，则①电子运动速率②电子的动能③电子运动周期④电子在半径为r的轨道上所具有的电势能⑤等效电流由以上各式可见，电子绕核运动的轨道半径越大，电子的运行速率越小，动能越小，电子运动的周期越大．在各轨道上具有的电视能越大。
原子跃迁时光谱线条数的确定方法:1．直接跃迁与间接跃迁原子从一种能量状态跃迁到另一种能量状态时，有时可能是直接跃迁，有时可能是间接跃迁，两种情况辐射(或吸收)光子的频率可能不同。
2．一群原子和一个原子氧原子核外只有一个电子，这个电子在某个时刻只能处在某一个可能的轨道上，在某段时间内，由某一轨道跃迁到另一个轨道时，可能的情况只有一种，但是如果容器中盛有大量的氢原子，这些原子的核外电子跃迁时就会有各种情况出现了。
玻尔理论玻尔理论，又称玻尔原子论，是量子力学最早的发展方向之一。
它由丹麦物理学家尼尔斯·玻尔在20世纪早期提出，是对经典力学中的行星运动的类比和推广，被广泛认为是现代物理学的基石之一。
本文将详细介绍玻尔理论的基本原理、发展历程以及物理意义等方面的内容。
一、玻尔理论的基本原理玻尔理论的基本原理是，原子中的电子绕着原子核旋转并在不同的轨道上运动，每个轨道都对应一种能量状态。
这些轨道由一些固定的量子数来描述，电子在该轨道上的运动只能以某些特定的能量量子（即能量量子化）的形式存在，不能连续地进行。
玻尔理论基于下面两个假设：1.电子在原子内的运动是旋转而非运动，而且只有在确定的轨道上才能旋转；2.在该轨道上，电子的角动量是规定的，不会发生变化，电子在轨道上的能量也是规定的，不会变化。
基于上述假设，玻尔使用了量子条件来推导原子的能级结构，结果表明，电子在原子中所能具有的能量是量子化的，而且能量的量子数只能是一个自然数。
玻尔利用牛顿力学和库仑定律建立了一个简单的数学模型，这个模型用来描述电子在不同轨道上的运动状态。
这一模型成为了现代量子力学的基础之一，而且为认识原子和分子性质在物理学发展中起了关键作用。
二、玻尔理论的发展过程在19世纪晚期和20世纪初期，物理学家们已经通过研究原子光谱、电离现象和化学反应等现象展开了对原子的探索。
而这个领域的发展正是玻尔理论面世的背景和契机。
1900年，德国物理学家马克斯·普朗克提出了能量量子化的概念，从而开启了量子物理学的大门。
此后，量子理论得到了迅速的进展，但是对原子结构的理解仍然很有限。
1913年，玻尔提出了他的原子理论，用来解释原子光谱线上的谱线。
这个理论基于经典力学的公式，假设了电子在轨道上运动并将其运动状态量子化，使能量是离散的而不是连续的。
和量子力学有所不同的是，玻尔理论基于轨道和能量的概念来描述电子的运动状态，而不是以波函数的形式来描述。
随着量子力学的广泛应用和科学发展的进步，玻尔理论的内在瑕疵也逐渐显现出来。
玻尔原子理论
玻尔理论提出的前夜
经典理论失足于原子尺度
1911年卢瑟福建立原子核式结构模型，表明原子由原子核与电子组成，而电子就像一群孩子一样围着火堆跳着圆圈舞，这火堆正是原子核。
这一模型成功地解释了α粒子散射实验，但是一旦运用牛顿力学与经典电磁理论来仔细一下分析这一模型则会发现它与事实存在着很大的矛盾，是站不住脚的。
如果按照经典电磁理论来推导，电子在绕核运动的过程中必将不断地辐射电磁波，电子也将因此不断损失能量最终坠落到原子核上，这样一来原子就必将是一个不稳定的结构。
其次，辐射电磁波的频率应当等于电子绕核转动的频率，既然电子在损失能量的过程中就像坠落地球的陨石一样随着不断地靠近绕转频率做出连续性地变化，那么其辐射出的电磁波频率也应当是连续变化的。
然而事实上，原子的结构是稳定的，并不会出现电子坠落到原子核上的现象，这是难以想象的，否则它也不会得到原子的称号，因为“原子”（atom）一词的原意就是“不可分”，而且观察表明原子辐射总是辐射具有特定频率的分立的光波（线光谱），一般不会出现不断改变的连续谱。
经典理论在原子的尺度上受到了挑战，而且这并不是说当时没能出现某个天才人物，能够运用已有的经典理论建立一个适用于原子内部的模型，而是只要运用经典理论就不可能得到合理的理论，无论理论的建立者是怎样的天才。
打个不恰当的比喻，这看起来有点儿像阴沟里翻船，经典理论陷入原子的泥潭中难以抽身。
但不论怎样，现在亟须建立起一个不同于经典理论的新理论，来描述在原子尺度上发生的奇怪现象。
复杂的氢原子光谱
且不谈古圣先贤们对于彩虹的研究和关于光谱的种种充满想象力的理论，在玻尔理论提出之前，至少是从牛顿开始，人们就已经积累了大量关于原子光谱的实验数据，尤其是在夫琅和费开拓性的发明了光柵之后。
但这些全都是经验性的，如果谈及理论即使是对原子光谱了解得再多的科学家也是一句话都说不出来，当时确实是出现了一些理论，像巴尔末公式、瑞兹公式，但这些理论都只是对数据做出了解释与预言，并未解释为什么会出现光谱，就像玻尔常常说的：瑞兹理论求出的那些谱线到底实际上是否存在是一个“离奇莫测”的问题。
而事实上氢原子作为自然界中最简单的原子，其谱线也被人们研究的最透彻，但其谱线的复杂程度是却人们没有料想到的，因此想要解决原子结构的问题，得先拿氢原子开刀。
玻尔原子理论的建立
玻尔的基本假设
玻尔的假设是在卢瑟福理论的基础上建立的，因此没有脱离卢瑟福的原子核式结构模型，在玻尔的理论当中，原子核依然是静止的，电子也绕核做圆周运动。
但为了解决经典理论在解决原子问题上遇到的尴尬，玻尔提出了几点与经典力学和电磁学格格不入的假设。
首先，玻尔注意到原子光谱具有分立的波长这一事实，因而假设原子内的能量是分立存在的，以E1、E2、E3…等表示。
又因为原子核是稳定的，所以他假设处于上述分立状态的原子是稳定的，而绕核转动的电子并不向外辐射电磁波，这些稳定的状态被称为定态。
于是玻尔就进一步假设只有当原子从一个一个定态跃迁到另一个定态的过程中才可能会吸收或发射光波。
现假设有m和n两个定态，且E m>E n，则当处于m定态的原子要跃迁到n定态时，它就要失去一部分能量，而这部分能量以光波的形式放出；当处于n态的原子要跃迁到m态时就要吸收一定频率的光波来补充能量。
而在这两个过程中吸收和放出的光波的频率ν与E m、E n存在下列关系
hν=E m-E n
其中h为普朗克常量。
运用玻尔原子理论解释氢原子光谱
玻尔在以上假设的基础上推导出了氢原子能级公式。
首先，记氢原子核外电子绕核运动的半径为r，则电子受到的库伦力作用为
(1)
其中Z为原子序数，对于氢原子来说，原子序数Z=1。
而ε0为真空介电系数，ε0≈8.85×10﹣¹²F /m。
根据牛顿定律，库仑引力应等于电子做圆周运动的向心加速度
(2)
其中v为电子绕核转动的线速度。
所以电子的总能量就包含两方面：运动时产生的动能与在电场中的电势能
(3)
综合以上两式可的电子的总能量
或(4) 以上推导均限于经典理论。
而为了与假设一致，得出分立的能量值，玻尔受到了普朗克量子理论的启发，提出电子的角动量是量子化的(电子受到的库仑力为有心力，角动量守恒)。
由于普朗克常数 具有角动量的量纲，玻尔假设电子角动量等于 的整数倍
m e vr=nh /2πn=1,2,3 (5)
将其代入式（2），便可的到量子化的速度和半径
n=1,2, (6)
n=1,2, (7)
将v n代入（4）式可得：
n=1,2, (9)
这样便得到了符合玻尔假设的分立的能量值。
为了使式子得到简化，不妨引入一无量纲数
通过计算可这α=7.29735308×10﹣³约为1 /137.
现在即可将v n,r n以及E n分别表示为：
v n=αcZ /n n=1,2, (10)
10米其中a0称为玻尔半径，常做原子线度的标志，它的值等于0.529166×10-
（13）
E n为负值，所以当n=1时原子的能量最低，处于此状态被称为原子的基态。
此状态下对应的v1，r1分别表示基态下电子的绕行速度和半径。
对于氢原子来说
v1=αc (14)
r1=a0 (15)
E₁=﹣½m e c²α²(16)
玻尔的原子模型经过计算得出的数据与前人得出的实验测量符合得很好，由此证实了玻尔关于原子能级的假设。
利用波粒二象性推导玻尔模型
我们不妨换一个角度来看玻尔的原子理论。
首先，我们依旧假设电子绕原子核运动，并且在此过程中不辐射电磁波。
那么根据德布罗意的理论，实物粒子如电子也具有波动性，不妨把它看成波长λ=h/mv的绕原子核运行的波，那么不难得出结论这样的波只能在周长为波长整数倍的圆轨道上存在，否则，在运行的过程中波峰和波谷势必会发生重叠，这样的波就不可能存在。
所以可以得出这样一个式子
n=1,2, (17)
由（2）式可知
(18)
(19)
将式（18）（19）分别代入式（17）中可得
n=1,2 (20)
n=1,2 (21)
再将代入式（20）（21）代入（3）式可得
n=1,2, (22)
有由于普朗克常量间存在着这样的数量关系
所以通过波粒二象性推导得出的式子与运用角动量守恒推导出的式子完全一致。
玻尔原子理论的局限性
尽管玻尔原子理论经过了诸如椭圆轨道、核动效应等的改进与完善，实验结果也得以与预言更加吻合，但是它依然存在根本上的局限，它只能解释氢原子与部分类氢原子的光谱，如把理论用于其它原子时,理论结果与实验不符,且不能求出谱线的强度及相邻谱线之间的宽度.这些缺陷主要是由于把微观粒子(电子,原子等)看作是经典力学中的质点,从而把经典力学规律强加于微观粒子上(如轨道概念)而导致的.也就是说,波尔没有完全抛弃经典理论,试图在经典和量子之间调和矛盾,这在文章的开头已经提到过了，是不可能的。
这很正常，那时的物理学界正经历着大变动，物理学所构建的世界图像历经了一次又一次的冲击。
一方面十九世纪是经典物理学作为一种理论体系而接近完善的时期，它已经形成了固定的模板，人们甚至乐观地认为物理学的工作已经结束。
“雨声犹在云，风声已到树”，自从普朗克打响物理学革命的第一枪之后，物理学的新理论也在这时发展起来，逐渐打破这人们对经典理论天国般的幻想。
处于这样一种时期，任何一个人都很难不受到旧有理论的局限，即使能，也未必有这样的勇气，同时，就算是经典理论的忠实捍卫者也肯定会忍不住朝新理论偷看几眼，否则岂不是“大事已了，如丧考妣”。
这样一来玻尔原子理论中经典理论与量子理论杂交的现象也就不足为奇了。
另外玻尔模型中的量子条件完全是人为附加的,无法从逻辑上加以说明。
它无法解释为什么处于定态中的电子不发出电磁辐射,对跃迁的过程描写也非常含糊,无法揭不氢原子光谱的强度和精细结构。
因此,玻尔在获年度诺贝尔物理学奖时说“这一理论还处于很初级的阶段,许多基本问题还有待解决。
”直到1925年,海森伯抛弃玻尔所采用的电子轨道、运行周期等经典概念,建立了全新的量子力学,玻尔模型才完成了其历史使命。
参考书目：《原子物理学》史斌星著《尼尔斯·玻尔——他的生平、学术和思想》戈革著。
