异面直线夹角的求法

异面直线所成角的几种求法仅供学习与交流，如有侵权请联系网站删除 谢谢2异面直线所成角的几种求法异面直线所成角的大小，是由空间一点分别引它们的平行线所成的锐角（或直角）来定义的。

因此，通常我们要求异面直线所成的角会要求学生通过平移直线，形成角，然后在某个三角形中求出角的方法来得到异面直线所成角的大小。

在这一方法中，平移直线是求异面直线所成角的关键，而如何平移直线要求学生有良好的空间观和作图能力。

一、向量法求异面直线所成的角例1：如图，在正方体ABCD-A 1B 1C 1D 1中，E 、F 分别是相邻两侧面BCC 1B 1及CDD 1C 1的中心。

求A 1E 和B 1F 所成的角的大小。

解法一：（作图法）作图关键是平移直线，可平移其中一条直线，也可平移两条直线到某个点上。

作法：连结B 1E ，取B 1E 中点G 及A 1B 1中点H ， 连结GH ，有GH//A 1E 。

过F 作CD 的平行线RS ， 分别交CC 1、DD 1于点R 、S ，连结SH ，连结GS 。

由B 1H//C 1D 1//FS ，B 1H=FS ，可得B 1F//SH 。

在△GHS 中，设正方体边长为a 。

GH=46a （作直线GQ//BC 交BB 1于点Q ， B A CD FEB 1 A 1 D 1C 1G HSRPQ仅供学习与交流，如有侵权请联系网站删除 谢谢3连QH ，可知△GQH 为直角三角形），HS=26a （连A 1S ，可知△HA 1S 为直角三角形）， GS=426a （作直线GP 交BC 于点P ，连PD ，可知四边形GPDS 为直角梯形）。

∴Cos ∠GHS=61。

所以直线A 1E 与直线B 1F解法二：（向量法）分析：因为给出的立体图形是一个正方体， 所以可以在空间建立直角坐标系，从而可以利用 点的坐标表示出空间中每一个向量，从而可以用 向量的方法来求出两条直线间的夹角。

以B 为原点，BC 为x 轴，BA 为y 轴，BB 1为z 轴，设BC 长度为2。

求异面直线所成的角求异面直线所成的角，一般有两种方法，一种是几何法，这是高二数学人教版（A ）版本倡导的传统的方法，其基本解题思路是“异面化共面，认定再计算”，即利用平移法和补形法将两条异面直线转化到同一个三角形中，结合余弦定理来求。

还有一种方法是向量法，即建立空间直角坐标系，利用向量的代数法和几何法求解，这是高二数学人教版（B ）倡导的方法，下面举例说明两种方法的应用。

例：长方体ABCD －A 1B 1C 1D 1中，AB=AA 1=2cm ，AD=1cm ，求异面直线A 1C 1与BD 1所成的角。

解法1：平移法设A 1C 1与B 1D 1交于O ，取B 1B 中点E ，连接OE ，因为OE//D 1B ，所以∠C 1OE 或其补角就是异面直线A 1C 1与BD 1所成的角△C 1OE 中211E B C B E C 2312221BD 21OE 25C A 21OC 22212111221111=+=+==++⋅====()552325222325OEOC 2E C OE OC OE C cos 2221212211=⨯⨯-⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=⋅-+=∠所以55a r c c o sOE C 1=∠所以 所以异面直线111BD C A 与所成的角为55arccos图1解法2：补形法在长方体ABCD —A 1B 1C 1D 1的面BC 1上补上一个同样大小的长方体，将AC 平移到BE ，则∠D 1BE 或其补角就是异面直线A 1C 1与BD 1所成的角，在△BD 1E 中，BD 1=3，5BE =，5224E D 221=+=()()555325253BE BD 2E D BE BD BE D cos 2221212211-=⨯⨯-+=⋅-+=∠所以异面直线A 1C 1与BD 1所成的角为55arccos图2解法3：利用公式21cos cos cos θθθ⋅=设OA 是平面α的一条斜线，OB 是OA 在α内的射影，OC 是平面α内过O 的任意一条直线，设OA 与OC 、OA 与OB 、OB 与OC 所成的角分别是θ、θ1、θ2，则21cos cos cos θθθ⋅=（注：在上述题设条件中，把平面α内的OC 换成平面α内不经过O 点的任意一条直线，则上述结论同样成立）D 1B 在平面ABCD 内射影是BD ，AC 看作是底面ABCD 内不经过B 点的一条直线，BD 与AC 所成的角为∠AOD ，D 1B 与BD 所成角为∠D 1BD ，设D 1B 与AC 所成角为θ，AOD cos BD D cos cos 1∠⋅∠=θ，55BD BD BD D cos 11==∠。

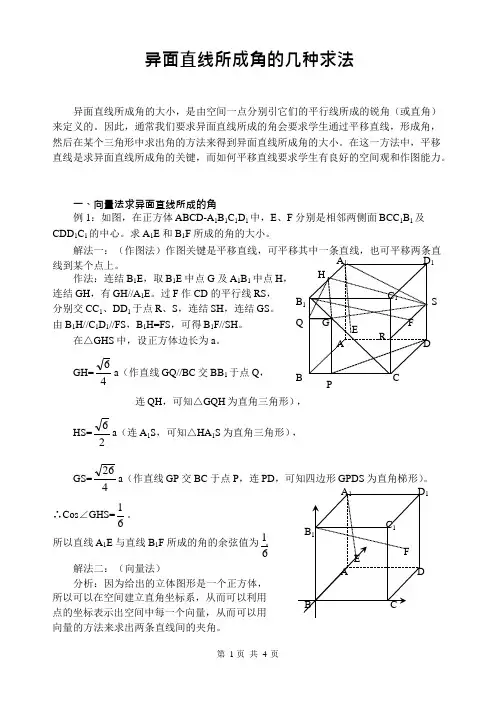
一、 等角定理：一个角的二边分别取另一个角的二边仄止，
则二个角相等或者互补.之阳早格格创做
二：同里曲线夹角
（1）意思：（2）0，]
注：二同里曲线夹角为
时，也喊干二曲线互相笔曲. 三、同里曲线夹角的供法：
1、仄移没有改变线段少度[主要适用于柱体]{曲交法}
2 .A1B1C1—ABC 是曲三棱柱，∠BCA=90°，面D1、F1分别是A1B1、A1C1的中面
若BC=CA=CC1，供BD1取AF1所成角的余弦值. 3.正在棱少为1的正圆体ABCD —A1B1C1D1中，M 战N 分别为A1B1
战BB1的中面，
供曲线A 取CN 所成角的余弦值
二、仄移改变线段少度[主要适用于锥体] 注：采用仄移目标的规则：正在二条同里曲线上，各采用一个面产死线段，则该线段的中面便是仄移的目标位子.
注：正三棱锥对于棱笔曲.[本量]
三、补形[主要适用于线段的位子没有简单爆收移动，如体对于角线，共时央供正在准则的柱体中如正圆体、少圆体中战一些正棱柱中] 例：正圆体ABCD －中，供同里曲线所成的角. B 1 (第6题) A 1 A B C 1 D 1
C
D M
N (第5题) F 1
A B C D 1
C 1
A 1
B 1。

异面直线所成的角一、平移法：常见三种平移方法：直接平移：中位线平移（尤其是图中出现了中点）：补形平移法：“补形法”是立体几何中一种常见的方法，通过补形，可将问题转化为易于研究的几何体来处理，利用“补形法”找两异面直线所成的角也是常用的方法之一。

直角平移法：1．在空间四边形ABCD 中，AD ＝BC ＝2，E ，F 分别为AB 、CD 的中点，EF ＝3，求AD 、BC 所成角的大小．解：设BD 的中点G ，连接FG ，EG 。

在△EFG 中 EF ＝3FG ＝EG ＝1∴∠EGF ＝120° ∴AD 与BC 成60°的角。

2．正∆ABC 的边长为a ，S 为∆ABC 所在平面外的一点，SA ＝SB ＝SC ＝a ，E ，F 分别是SC和AB 的中点．求异面直线SA 和EF 所成角． 正确答案：45°3．S 是正三角形ABC 所在平面外的一点，如图SA ＝SB ＝SC ，且∠ASB ＝∠BSC ＝∠CSA＝2π，M 、N 分别是AB 和SC 的中点．求异面直线SM 与BN 所成的角的余弦值． 证明：连结CM ，设Q 为CM 的中点，连结QN ，则QN ∥SM∴∠QNB 是SM 与BN 所成的角或其补角 连结BQ ，设SC ＝a ，在△BQN 中 BN ＝a 25 NQ ＝21SM ＝42a BQ ＝a 414∴COS ∠QNB ＝5102222=⋅-+NQ BN BQ NQ BN4．如图，在直三棱柱ABC －A 1B 1C 1中，∠BCA ＝90°，M 、N 分别是A 1B 1和A 1C 1的中点，若BC ＝CA ＝CC 1，求BM 与AN 所成的角．解：连接MN ，作NG ∥BM 交BC 于G ，连接AG ， 易证∠GNA 是BM 与AN 所成的角．设：BC ＝CA ＝CC 1＝2，则AG ＝AN ＝5，GN ＝BM ＝6， cos ∠GNA ＝1030562556=⨯⨯-+。

专题6：立体几何中异面直线的夹角几何法（解析版）异面直线成角步骤：1、平移，转化为相交直线所成角；2、找锐角（或直角）作为夹角；3、求解注意：取值范围：（0。

,90。

]. 1．如图，四边形ABCD 是边长为2的正方形，PD ⊥面ABCD ，直线PA 与直线BC 所成角大小为60°．（1）求证：平面PAC ⊥平面PBD ； （2）求异面直线PC 与BD 所成角大小． 【答案】（1）证明见解析；（2）2arccos 4. 【分析】（1）根据线面垂直的判定定理，先证明AC ⊥面PBD ；再由面面垂直的判定定理，即可得出结论成立；（2）设正方形ABCD 的中心为O ，PA 中点为E ，连接OE ，则//OE PC ，得到EOD ∠（或其补角）是异面直线PC 与BD 所成角，结合题中条件，即可求出结果. 【详解】（1）证明：∵PD ⊥平面ABCD ，AC ⊂平面ABCD ，∴PD AC ⊥，又∵BD AC ⊥，PD BD D ⋂=，PD ⊂面PBD ，BD ⊂面PBD ，∴AC ⊥面PBD ， ∵AC ⊂面PAC ，∴平面PAC ⊥平面PBD ；（2）设正方形ABCD 的中心为O ，PA 中点为E ，连接OE ，ED ，则//OE PC ， ∴EOD ∠（或其补角）是异面直线PC 与BD 所成角， ∵60PAD ∠=︒，∴23PD =2ED =， 又4PC =，∴2OE =，2OD =∴2222cos 2222EO OD ED EOD EO OD +-∠===⋅⋅⋅， ∴直线PB 与直线AC 所成角大小为2arccos4．【点睛】本题主要考查证明面面垂直，考查求异面直线所成的角，属于常考题型.2．空间四边形ABCD 中，AB CD =，点M N 、分别为对角线BD 、AC 的中点.（1）若直线AB 与MN 所成角为60︒，求直线AB 与CD 所成角的大小； （2）若直线AB 与CD 所成角为θ，求直线AB 与MN 所成角的大小. 【答案】（1）60︒；（2）2θ或1802θ︒-. 【分析】取AD 中点为P ，连接PM ，PN ，根据题中条件，由异面直线所成角的定义，得到MPN ∠即是直线AB 与CD 所成的角，或所成角的补角，PMN ∠为直线AB 与MN 所成的角，且PMN 为等腰三角形；（1）根据条件，得到60PMN ∠=︒，求出MPN ∠，即可得出结果； （2）根据条件，得到MPN θ∠=或180MPN θ∠=︒-，进而可求出结果. 【详解】取AD 中点为P ，连接PM ，PN ，因为点M N 、分别为对角线BD 、AC 的中点，所以//PM AB ，//PN CD ，且12PM AB =，12PN CD =，则MPN ∠即是直线AB 与CD 所成的角，或所成角的补角，PMN ∠为直线AB 与MN 所成的角，又AB CD =，所以PM PN =，即PMN 为等腰三角形；（1）若直线AB 与MN 所成角为60︒，即60PMN ∠=︒， 则18026060MPN ∠=︒-⨯︒=︒， 所以直线AB 与CD 所成角的大小为60︒； （2）若直线AB 与CD 所成角为θ， 则MPN θ∠=或180MPN θ∠=︒-，若MPN θ∠=，则18018022MPN PMN θ︒-∠︒-∠==，即直线AB 与MN 所成角的大小为1802θ︒-；若180MPN θ∠=︒-，则18022MPN PMN θ︒-∠∠==， 即直线AB 与MN 所成角的大小为2θ.综上， 直线AB 与MN 所成角的大小为1802θ︒-或2θ.【点睛】本题主要考查求异面直线所成的角，熟记异面直线所成角的定义即可，属于常考题型. 3．已知长方体1111ABCD A B C D -中，M ､N 分别是1BB 和BC 的中点，AB =4，AD =2，1215BB =，求异面直线1B D 与MN 所成角的余弦值.25【分析】如图，连接1B C ，则1B C ∥MN ，所以1DB C ∠为异面直线1B D 与MN 所成角，然后在直角三角形1DB C 中求解即可 【详解】解：如图，连接1B C ，因为M ､N 分别是1BB 和BC 的中点，所以1B C ∥MN ， 所以1DB C ∠为异面直线1B D 与MN 所成角，因为长方体1111ABCD A B C D -中，AB =4，AD =2，1215BB = 所以2221116441545DB AB AD BB =++=++⨯=，221141548B C BB BC =+=⨯+=，DC ⊥平面11BB C C ，所以1DC B C ⊥， 所以11125cos 545B C DB C DB ∠===， 所以异面直线1B D 与MN 25【点睛】此题考查求异面直线所成的角，考查转化思想和计算能力，属于基础题 4．如图所示，在正方体1111ABCD A B C D -中，M 、N 分别为1A A 、AB 的中点.（1）求证：1//MN D C ；（2）求异面直线MN 与1B C 所成角的大小. 【答案】（1）证明见解析；（2）60° 【分析】（1）易知1//MN A B ，11//D C A B ，根据平行的传递性得出结论;（2）由（1）的平行知异面直线MN 与1B C 所成成角是11B CD ∠（或其补角），在三角形中求得此角即可．（1）连接1A D ，∵M 、N 分别为1A A 、AB 的中点，∴1//MN A B ,正方体中，11A D 与BC 平行且相等，∴11A BCD 是平行四边形，∴11//D C A B ，所以1//MN D C ，（2）由（1）知异面直线MN 与1BC 所成成角是11B CD ∠（或其补角）， 在立方体中，1111B C CD D B ==11B CD ∴∆是等边三角形，∴11B CD ∠60=︒，∴异面直线MN 与1BC 所成成角是60°． 【点睛】本题考查证明线线平行以及求异面直线所成的角，属于基础题型.5．如图，已知长方体ABCD A B C D ''''-中，23AB =，23AD =，2AA '=.（1）BC 和A C ''所成的角是多少度？ （2）AA '和BC '所成的角是多少度？ 【答案】（1）45；（2）60（1）根据//BC B C ''可知所求角为A C B '''∠，由Rt A B C '''中的长度关系可求得结果； （2）根据//AA BB ''可知所求角为B BC ''∠，由Rt BB C ''△中的长度关系可求得结果. 【详解】（1）连接A C ''，//BC B C ''，∴异面直线BC 和A C ''所成角即为直线B C ''和A C ''所成角，即A C B '''∠，在Rt A B C '''中，23A B AB ''==，23B C AD ''==，tan 1A C B '''∴∠=，45A C B '''∴∠=，即异面直线BC 和A C ''所成角为45；（2）连接BC '，//AA BB ''，∴异面直线AA '和BC '所成角即为直线BB '和BC '所成角，即B BC ''∠，在Rt BB C ''△中，23B C AD ''==，2BB AA ''==，tan 3B BC ''∴∠=60B BC ''∴∠=，即异面直线AA '和BC '所成角为60.【点睛】本题考查立体几何中异面直线所成角的求解问题，关键是能够通过平行关系将异面直线所成角转化为相交直线所成角的求解问题.6．已知ABCD ﹣A 1B 1C 1D 1是棱长为a 的正方体． （1）求直线DA 1与BC 所成角； （2）求直线D 1A 与BA 1所成角； （3）求直线BD 1和AC 所成角．【答案】（1）4π （2）3π （3）2π【分析】（1）由//AD BC 得1DAD ∠是直线1DA 与BC 所成角，求出1DAD ∠即可得解； （2）由11//AD C B 得11C BA ∠是直线1D A 与1BA 所成角,求出11C BA ∠即可得解； （3）证明AC ⊥平面1BDD 后即可得1AC BD ⊥，即可得解. 【详解】（1）正方体1111ABCD A B C D -是棱长为a 的正方体， ∵//AD BC ，∴1ADA ∠是直线1DA 与BC 所成角， ∵1AD AA ＝，1AD AA ⊥，∴14ADA π∠=，∴直线1DA 与BC 所成角为4π． （2）∵11//AD C B ，∴11C BA ∠是直线1D A 与1BA 所成角， ∵1111BA AC BC ==，∴ 113C BA π∠=，∴直线1D A 与1BA 所成角为3π． （3）∵四边形ABCD 是正方形，∴AC BD ⊥，∵正方体1111ABCD A B C D -中，1DD ⊥平面ABCD ，AC ⊂平面ABCD ， ∴1DD AC ⊥， ∵1DD BD D =，∴AC ⊥平面1BDD ，∵1BD ⊂平面1BDD ，∴1AC BD ⊥， ∴直线1BD 和AC 所成角为2π．【点睛】本题考查了异面直线夹角的求法及线面垂直的判定和性质，属于基础题.7．如图所示，空间四边形ABCD 中，AB CD =，AB CD ⊥，E ，F 分别为BC ，AD 的中点，求EF 和AB 所成角的大小.【答案】45°. 【分析】取BD 的中点G ，连接,EG FG ，根据题意可得GFE ∠（或其补角）即为EF 与AB 所成角，由EG GF =，AB CD ⊥，可得EFG ∆为等腰直角三角形，进而可求解. 【详解】如图所示，取BD 的中点G ，连接,EG FG .∵,E F 分别为,BC AD 的中点， 且,//,//AB CD EG CD GF AB =∴，且11,22EG CD GF AB ==，即EG GF =， GFE （或其补角）即为EF 与AB 所成角.,,90AB CD EG GF EGF ︒⊥∴⊥∴∠=，EFG ∴∆为等腰直角三角形，45GFE ︒∴∠=，即EF 与AB 所成角的大小为45°.【点睛】本题考查了异面直线所成的角，解得的关键是找出与异面直线所成角相等的角，属于基础题. 8．正三棱锥S ABC -的侧棱长与底面边长都为a ,,E F 分别是,SC AB 的中点,求直线EF 和SA 所成的角.【答案】45° 【分析】取SB 的中点G ,连接,,,EG GF SF CF ，于是异面直线SA 与EF 所成的角就是直线FG 与EF 所成的角,即为EFG (或其补角)，在EFG ∆中求解.【详解】解析 如图,取SB 的中点G ,连接,,,EG GF SF CF .在SAB ∆中,,F G 分别是AB ,SB 的中点,//FG SA ∴,且12FG SA =.于是异面直线SA 与EF 所成的角就是直线FG 与EF 所成的角,即为EFG (或其补角).在SAB 中,SA SB a ==,12AF FB a ==, SF AB ∴⊥,且3SF a =.同理可得CF AB ⊥,且3CF =. 在SFC 中,32SF CF a ==,SE EC =, FE SC ∴⊥,且2222FE SF SE a =-=. 在SAB 中,FG 是中位线,122a FG SA ==. 在SBC 中,GE 是中位线,122a GE BC ∴==. 在EGF △中,22222a FG GE FE +==,EGF ∴是以FGE ∠为直角的等腰直角三角形,45EFG ︒∴∠=.∴异面直线SA 与EF 所成的角为45°. 【点睛】本题考查异面直线所成角，意在考查空间想象能力，和基本的证明方法，属于基础题型. 9．在四棱锥A BCDE -中,底面BCDE 为梯形,//BC DE .设,,,CD BE AE AD 的中点分别为,,,M N P Q .若AC DE ⊥,且3AC BC =,求异面直线DE 与PN 所成角的大小. 【答案】（2）60°. 【分析】由条件可知ABC ∠(或其补角)即为异面直线DE 与PN 所成的角，再求解. 【详解】解析 (2)因为PN 为ABE ∆的中位线, 所以//PN AB .又//BC DE ,所以ABC ∠(或其补角)即为异面直线DE 与PN 所成的角. 又AC DE ⊥,所以AC BC ⊥. 在Rt ACB △中,3tan 3AC BCABC BC ∠===所以60ABC ︒∠=. 所以异面直线DE 与PN 成的角为60°. 【点睛】本题考查四点共面和异面直线所成的角，意在考查推理，证明能力，属于基础题型. 10．如图,在三棱柱111ABC A B C -中,1AA 与,AC AB 所成的角均为60°,90BAC ︒∠=,且1AB AC AA ==,求异面直线1A B 与1AC 所成角的余弦值.【答案】33【分析】首先利用补体，将三棱柱补为四棱柱1111ABDC A B D C -，由条件可知11//AC BD ， 则11A BD ∠(或其补角)就是异面直线1A B 与1AC 所成的角，根据三边关系求11cos A BD ∠. 【详解】解析 如图所示,把三棱柱补为四棱柱1111ABDC A B D C -,连接111,,BD A D AD ,由四棱柱的性质知11//BD AC ,则11A BD ∠(或其补角)就是异面直线1A B 与1AC 所成的角. 设AB a ,1AA 与AC ,AB 所成的角均为60°,且1AB AC AA ==,1A B a ∴=,1112cos303BD AC AA a︒==⋅=.又90BAC ︒∠=,在矩形ABDC 中,2AD a =,112A D a ∴=,2221111A D A B BD ∴+=,1190BA D ︒∴∠=,在11Rt BA D 中,11113cos 33A B A BD BD a∠===. 【点睛】本题考查异面直线所成角的余弦值，意在考查空间想象能力和计算能力，属于基础题型. 11．如图，在长方体ABCD A B C D ''''-中，23AB AD ==，2AA '=，求：（1）直线BC 和A C ''所成的角的大小； （2）直线AA '和BC '所成的角的大小. 【答案】（1）45°.（2）60°. 【分析】（1）确定B C A '''∠是异面直线A C ''与BC 所成的角，在Rt A B C '''中根据长度关系得到答案。

两异面直线所成的角的范围
两异面直线所成的角的范围，一般来说是介于0度到180度之间。

而如果两条直线平行，也就是说它们是同面的，那么它们之间所成的
夹角就是0度。

而当两条直线垂直的时候，也就是它们是垂直的异面
直线，所以它们之间所成的夹角就是90度。

因此，两条异面直线之间
所成的夹角一般都是在0度到180度之间。

另外，在数学上，所谓的“异面直线”其实指的是起点不同，方
向相同的两条直线，因此这两条直线是有可能重合的，即它们所成角
度可能大于180度，甚至是360度，但是它们依然是异面直线。

再比如，如果两条异面直线为AB和CD，它们之间所成的夹角可以
通过以下几种方法来进行求解：
1、求出AB和CD的各自斜率，然后用两个向量的数量积求出其夹角；
2、把AB和CD分别看作两个向量，并且求出它们的向量积；
3、先求出AB和CD的向量积，再将其转化为弧度，最后将弧度转
化为角度；
4、使用三角函数进行求解。

因此，总结而言，两异面直线之间所成的角度一般都是介于0度
到180度之间，但也有可能大于180度，甚至是360度，而如果两条
异面直线重合，那么它们之间所成的夹角就是360度，而且它们也是
异面直线，只是它们的起点相同，方向也相同而已。

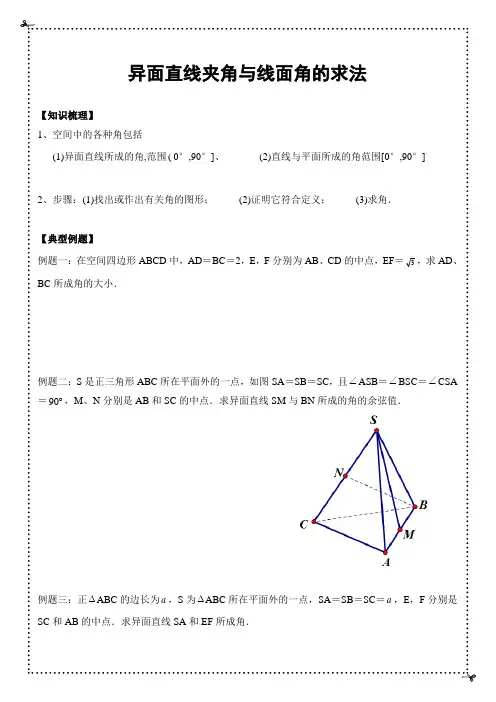
两异面直线所成的角题目解法大全（配有高考真题练习题）异面直线所成角的求法例一、已知正四棱锥P—ABCD侧棱长与底面边长相等，E、F分别为PC、PD的中点，求异面直线BE与CF所成的角的余弦值.绿色通道：法一、BE不动，在面PDC内过点E平移CF；法二、CF不动，过F平移EB，其中是以平行四边形BEFH为依托；法三、利用空间向量知识来求解.解法一：如下图1，设正四棱锥的侧棱长与底面边长为2，在面PDC内过E作EG平行于∠或其补角为BE与CF所成角. BD=22,又PB=PD=2, CF，交PD于G，连结BG. 则BEG所以BPD ∠为直角, BG 2=PB 2+PD 2=22+2)21(=417.又CF=3, EG=23.在BEG∆中,cos BEG ∠=EG BE BG EG BE .2222-+= —61，所以BE 与CF 所成角是BEG ∠的补角，大小CBAP为arccos61. 解法二：如上图2.设各棱长均为2，H 为AB 的中点，连结EF ，FH ，则EF=BH //21CD ，∴BEFH 为平行四边形，FH //BE ，∴∠CFH 为BE 与CF 所成的角,且FH=BE=3.连结HC ，则HC=5,CF=3.在∆CFH 中，cos ∠CFH = FH CF CH FH CF ⋅-+2222=61,所以BE 与CF 所成角大小为arccos61.解法三：如上图.建立空间直角坐标系 .设各棱长均为2, PO=2，则 B (2,0,0 ), C( 0,2,0), E(0,22，22)，F(—22，0，22) , 则= (—2，22，22)，=（—22，—2，22），与的夹角为θ， cos θ61，所以BE 与CF 所成的角为arccos 61. 例题1：如图：表示正方体1111D C B A ABCD -，求异面直线11CC BA 和所成的角。

例2．空间四边形ABCD 中，2AD BC ==，,E F 分别是,AB CD的中点，EF =求异面直线,AD BC 所成的角。

异面直线夹角【考点例题解析】一、平移法：常见三种平移方法：直接平移：中位线平移（尤其是图中出现了中点）：补形平移法：“补形法”是立体几何中一种常见的方法，通过补形，可将问题转化为易于研究的几何体来处理，利用“补形法”找两异面直线所成的角也是常用的方法之一。

直接平移法1．在空间四边形ABCD 中，AD ＝BC ＝2，E ，F 分别为AB 、CD 的中点，EF ＝3，求AD 、BC 所成角的大小．2．正∆ABC 的边长为a ，S 为∆ABC 所在平面外的一点，SA ＝SB ＝SC ＝a ，E ，F 分别是SC 和AB 的中点．求异面直线SA 和EF 所成角．3．S 是正三角形ABC 所在平面外的一点，如图SA ＝SB ＝SC ，且∠ASB ＝∠BSC ＝∠CSA ＝2π，M 、N 分别是AB 和SC 的中点．求异面直线SM 与BN 所成的角的余弦值．BM AN CSABCD A 1B 1C 1D 1EF4．如图，在直三棱柱ABC －A 1B 1C 1中，∠BCA ＝90°，M 、N 分别是A 1B 1和A 1C 1的中点，若BC ＝CA ＝CC 1，求BM与AN 所成的角．5．如图，在正方体1111D C B A ABCD -中，E 、F 分别是1BB 、CD 的中点．求AE 与F D 1所成的角。

6．如图1—28的正方体中，E 是A ′D ′的中点(1)图中哪些棱所在的直线与直线BA ′成异面直线? (2)求直线BA ′和CC ′所成的角的大小； (3)求直线AE 和CC ′所成的角的正切值； (4)求直线AE 和BA ′所成的角的余弦值7. 长方体ABCD —A 1B 1C 1D 1中，若AB=BC=3，AA 1=4，求异面直线B 1D 与BC 1所成角的大小。

B '(图1－28)A 'ABC 'D 'CD FE2.中位线平移法：构造三角形找中位线，然后利用中位线的性质，将异面直线所成的角转化为平面问题，解三角形求之。

异面直线的夹角-线面角(含答案)空间角1、异面直线所成角的求法一是几何法，二是向量法。

异面直线所成的角的范围：]2,0(π几何法求异面直线所成角的思路是：通过平移把空间两异面直线转化为同一平面内的相交直线，进而利用平面几何知识求解。

基本思路是选择合适的点，平移异面直线中的一条或两条成为相交直线，这里的点通常选择特殊位置的点。

常见三种平移方法：直接平移：中位线平移（尤其是图中出现了中点）：补形平移法：“补形法”是立体几何中一种常见的方法，通过补形，可将问题转化为易于研究的几何体来处理，利用“补形法”找两异面直线所成的角也是常用的方法之一。

例1在正方体ABCD A B C D ''''-中，E 是AB 的中点，（1）求BA /与CC /夹角的度数. （2）求BA /与CB /夹角的度数．(3)求A /E 与CB /夹角的余弦值．例2：长方体ABCD —A 1B 1C 1D 1中，若AB=BC=3，AA 1=4，求异面直线B 1D 与BC 1所成角的余弦值。

直接平移：常见的利用其中一个直线a 和另一个直线b 上的一个已知点，构成一个平面，在此平面内做直线a 的平行线。

解法一：如图④，过B 1点作BE ∥BC 1交CB 的延长线于E 点。

则∠DB 1E 就是异面直线DB 1与BC 1所成角，连结DE 交AB 于M ，DE=2DM=35，cos∠DB1E=734解法二：如图⑤，在平面D1DBB1中过B点作BE∥DB1交D1B1的延长线于E，则∠C1BE就是异面直线DB1与BC1所成的角，连结C1E，在△B1C1E中，∠C1B1E=135°，C1E=35，cos∠C1BE=734170课堂思考：1.如图，PA 矩形ABCD，已知PA=AB=8，BC=10，求AD与PC所成角的余切值为。

DC1B1A1CD2.在长方体ABCD- A1B1C1D1中，若棱B B1=BC=1，AB=3，求D B和AC所成角的余弦值.例3 如图所示，长方体A1B1C1D1-ABCD中，∠ABA1=45°,∠A1AD1=60°,求异面直线A1B与AD1所成的角的度数.课堂练习如图空间四边形ABCD中，四条棱AB，BC，CD，DA及对角线AC，BD均相等，E为AD的中点，F为BC中，（1）求直线AB和CE 所成的角的余弦值。

两条异面直线所成的夹角、直线与平面所成的角与二面角讲义前言：立体几何的计算和证明常常涉及到二大问题：一是位置关系，它主要包括线线垂直，线面垂直，线 线平行，线面平行；二是度量问题，它主要包括点到线、点到面的距离，线线、线面所成角，面面所成 角等。

考点一：两条异面直线所成的夹角范围：两条异面直线所成的夹角的取值范围是 。

向量求法：设直线,a b 的方向向量为a,b ，其夹角为θ，则有cos ___________.θ= 点A ，B ∈直线a,C ，D ∈直线b 。

构成向量CD AB ,。

><⋅>=<CD AB CDAB CD AB CD AB ,,,cos 所对应的锐角或直角即为直线a(AB)与b(CD)所成的角。

随堂练习：1. 在正三棱柱ABC －A 1B 1C 1，若AB ＝2BB 1，则AB 1与C 1B 所成角的大小( )A ．60°B ．90°C ．105°D ．75°2．如图，A 1B 1C 1—ABC 是直三棱柱，∠BCA =90°，点D 1、F 1分别是A 1B 1、A 1C 1的中点，若BC =CA =CC 1， 则 BD 1与AF 1所成角的余弦值是（ ）A ．1030 B ．21 C ．1530 D ．10153、 如图1－6，在△ABC 中，∠ABC ＝60°，∠BAC ＝90°，AD 是BC 上的高，沿AD 把△ABD 折起，使∠BDC ＝90°.图1－6(1)证明：平面ADB ⊥平面BDC ；(2)设E 为BC 的中点，求AE →与DB →夹角的余弦值．考点二：直线与平面所成的角定义：直线与平面所成的角是指直线与它在这个平面内的射影所成的角。

范围：直线和平面所夹角的取值范围是 。

向量求法：设直线l 的方向向量为a ，平面的法向量为n ，直线与法向量所成角的余弦值为 |c o s |________θ=直线与平面所成的角为ϕ，则有sin ___________.ϕ=或在平面内任取一个向量m ，则|cos |___________.θ=.AP 与平面α的法向量n 所成的角所对应的锐角的余角或直角即为直线AP 与平面α所成的角θ，所以AP 与n 的角的余弦值的绝对值为直线AP 与平面α所成的角的正弦值。