【思维导图】BiJi-高等数学
- 格式:xmin
- 大小:69.95 KB
- 文档页数:1

大一数学知识点思维导图数学是一门重要的学科,大一学生正式接触数学课程时,常常会感到有些吃力。
为了帮助大家更好地掌握大一数学知识,我整理了一份思维导图,以系统地呈现大一数学的重要知识点。
以下是思维导图的内容:1. 微积分1.1 极限与连续性- 数列极限- 函数极限- 连续函数与间断1.2 导数与微分- 导数的定义- 导数的性质- 微分的应用1.3 积分与不定积分- 不定积分的定义- 不定积分的计算法则- 定积分及其应用2. 线性代数2.1 矩阵与线性方程组- 矩阵的基本概念- 矩阵的运算法则- 线性方程组的求解方法 2.2 行列式与特征值- 行列式的性质与计算方法 - 特征向量与特征值- 对角化与相似矩阵2.3 向量空间与线性变换- 向量空间的基本概念- 线性变换的定义与性质 - 线性变换的矩阵表示3. 概率论与数理统计3.1 概率的基本理论- 随机试验与样本空间- 事件与概率- 条件概率与独立性3.2 随机变量与概率分布- 随机变量的概念- 离散型随机变量与概率分布- 连续型随机变量与概率密度函数 3.3 统计推断与假设检验- 参数估计- 假设检验的基本原理- 常见的假设检验方法4. 微分方程4.1 常微分方程基础- 微分方程的基本概念- 一阶常微分方程的解法- 高阶常微分方程的解法4.2 线性常微分方程与特殊函数 - 齐次线性常微分方程- 非齐次线性常微分方程- 常见的特殊函数及其应用5. 数学分析5.1 数列与级数- 数列的极限- 级数的收敛与发散- 常见的级数及其性质5.2 函数与极限- 函数的极限与连续性- 函数的一致连续性- 函数的一致收敛5.3 多元函数微分学- 偏导数与全微分- 多元函数的极值- 隐函数与参数方程以上是大一数学的主要知识点思维导图,通过整理这份导图,希望能够帮助大家更好地理清数学知识的脉络,并对各个知识点有一个整体的认识。
当然,在实际学习中,还需要深入学习每个知识点的具体内容,理解其定义、原理及应用方法。

高等数学知识点思维导图高二在高二学习过程中,高等数学是一门具有较高难度的学科,需要对各种知识点进行系统性地学习和理解。
为了帮助大家更好地掌握高等数学知识,本文将以思维导图的形式呈现,旨在帮助同学们更好地理解和记忆相关内容。
一、微分与导数微分与导数是高等数学的基础概念,它们是研究函数变化的重要工具。
微分定义、导数的计算与性质是本章的核心内容。
1.1 微分的定义微分的定义是描述函数变化的基本工具,它是函数在某一点的变化率。
微分的定义可以用极限的概念表示,即:```f'(x) = lim (h->0) [f(x+h)-f(x)] / h```其中f'(x)表示函数f(x)在点x处的导数。
1.2 导数的计算导数的计算涉及到一系列的公式和求导法则,例如:- 常数函数的导数为0;- 幂函数的导数为幂次减一再乘以常数;- 指数函数和对数函数的导数有特定的计算方法。
通过掌握这些求导法则,可以简化导数的计算过程。
1.3 导数的性质导数的性质是指导数函数与原函数之间的关系。
导数具有如下性质:- 可导函数的连续性:可导函数一定是连续函数;- 导数与函数的单调性:函数的导数能够刻画函数的单调性;- 导数与函数的极值:函数取得极值的点是导数为零的点。
二、积分与不定积分积分与不定积分是高等数学中另一个重要的概念,它们是研究函数与其变化量之间的关系。
积分的定义、不定积分和定积分的计算方法是本章的重点内容。
2.1 积分的定义积分的定义是描述函数与其变化量之间的关系,它可以看作微分的逆运算。
积分的定义可以用极限的概念表示,即:```∫[a,b] f(x) dx = lim (n->∞) Σ[f(xi)Δx]```其中[a,b]表示积分的区间,f(x)表示被积函数,Σ表示求和符号。
2.2 不定积分不定积分是求解原函数的过程,它的结果可以表示为:```∫f(x) dx = F(x) + C```其中F(x)表示原函数,C为常数。


高数大一上知识点总结思维导图大学的第一学期,往往是高数课程的入门阶段。
在这个阶段里,学生们掌握了一些基本的高数概念和方法,如函数、极限、导数等。
这些知识点的理解和掌握,对于学生们后续的学习和发展有着重要的意义。
在本文中,我们将通过思维导图的方式,对高数大一上的知识点进行总结,以帮助学生们更好地复习和巩固这些知识。
第一部分:函数与极限函数与极限是高数的基础概念,也是日后学习微积分的基石。
函数是描述不同变量之间关系的一种工具,而极限则是函数在某个点上的趋势或趋近性质。
理解函数与极限的概念,对于后续的微分与积分的学习都非常重要。
第一章:函数的概念与性质- 函数的定义:自变量与因变量之间的关系。
- 函数的图像:描述函数在坐标系上的图形。
- 函数的性质:奇偶性、周期性等。
第二章:极限- 极限的定义:在无穷小的条件下,自变量趋近于某一值时,函数的趋势。
- 极限的计算:通过代入、画图等方法计算极限。
- 左右极限:自变量趋近于某一值时,函数的趋势在左侧和右侧是否相同。
第二部分:微分学微分学是高等数学中的一个重要分支,也是日后学习微积分的基础。
微分学主要研究函数在给定点的变化率和切线方程等问题。
第三章:导数- 导数的定义:函数在某一点上的瞬时变化率。
- 导函数的求法:求导的基本法则及常见函数的导数。
- 导数的应用:最值问题、凹凸性等。
第四章:微分- 微分的定义:函数在给定点上的变化量。
- 微分的计算:通过导数定义计算微分的近似值。
- 微分的应用:近似计算、最值问题等。
第三部分:积分学积分学是微分学的反向操作,主要研究函数的积分和曲线下的面积等问题。
积分学有广泛的应用领域,如物理学、经济学等。
第五章:不定积分- 不定积分的定义:函数在一定区间上的积分,得到的结果是原函数。
- 不定积分的计算:通过基本积分法则计算不定积分。
- 不定积分的应用:定积分的计算、面积、物理学中的应用等。
第六章:定积分- 定积分的定义:函数在一定区间上的积分,得到的结果是一个数值。
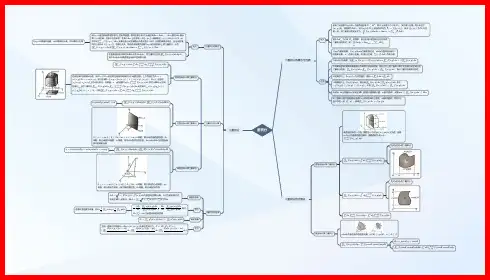

高中数学知识点思维导图
----21张图理清高中数学知识结构
目录
一、集合与简易逻辑 (1)
二、函数与基本初等函数 (2)
三、导数及其应用 (3)
四、三角函数 (4)
五、解三角形与平面向量 (5)
六、数列 (6)
七、不等式 (7)
八、三视图与空间位置关系 (8)
九、立体几何 (9)
十、空间向量与立体几何 (10)
十一、直线的方程 (11)
十二、圆的方程 (12)
十三、直线系、圆系、直线与圆锥曲线关系 (13)
十四、圆锥曲线 (14)
十五、椭圆的定义与几何性质 (15)
十六、双曲线的定义与几何性质 (16)
十七、抛物线的定义与几何性质 (17)
十八、计数原理、二项式定理、推理与证明 (18)
十九、概率与统计 (20)
二十、复数 (21)
二十一、算法 (22)
一、集合与简易逻辑
二、函数与基本初等函数
三、导数及其应用
四、三角函数
五、解三角形与平面向量
六、数列
七、不等式
八、三视图与空间位置关系
九、立体几何
十、空间向量与立体几何
十一、直线的方程
十二、圆的方程
十三、直线系、圆系、直线与圆锥曲线关系
十四、圆锥曲线
十五、椭圆的定义与几何性质
十八、计数原理、二项式定理、推理与证明
十九、概率与统计
二十、复数
二十一、算法。
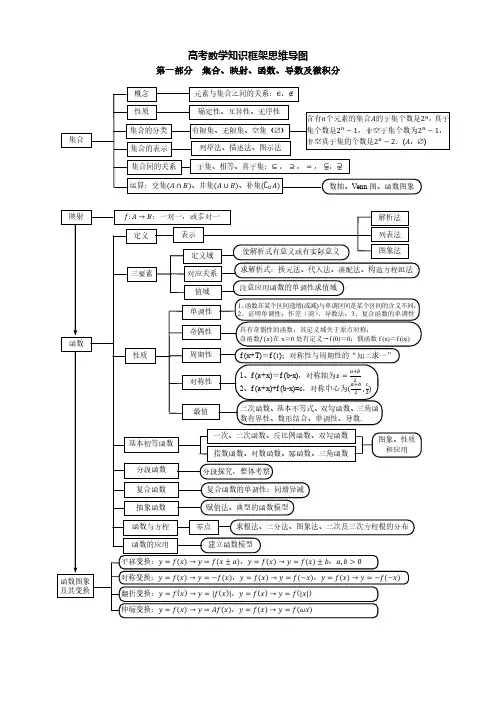
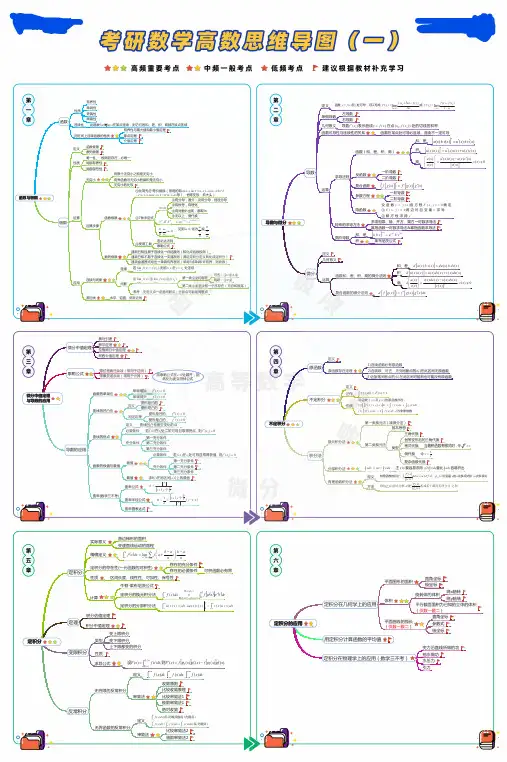

高数大一上知识点思维导图高等数学是大一学生必修的一门课程,因为其抽象性和难度较大,对很多同学来说是一项挑战。
为了更好地掌握高等数学的知识点,提高学习效果,我整理了一份高等数学大一上知识点的思维导图。
下面就让我们一起来看看这份思维导图吧!在高等数学大一上的学习中,主要包含了导数与微分、积分与不定积分、微分方程三个部分。
首先,让我们从导数与微分这一部分开始。
在导数与微分这一部分中,首先介绍了函数与极限的概念。
函数是高等数学的基础,它是自变量和因变量之间的关系。
而极限则是函数无限逼近某一点的过程,通过极限我们可以研究函数在一个点的性质。
接着介绍了导数的概念,导数是函数变化率的度量,表示函数在某一点的瞬时变化率。
在导数的求解中,我们需要掌握一些常用的导数公式和运算法则。
通过这些工具,我们可以求解导数问题,如求函数的导函数、求曲线的切线等。
接下来是积分与不定积分这一部分。
积分是导数的逆运算,表示函数在一定区间内的累积变化量。
不定积分则是求积分的一种方法,其中的不定积分常数表示在不同点处的积分结果可能不同。
在积分与不定积分的学习中,我们需要熟练掌握换元法、分部积分法和定积分的计算。
这些方法可以帮助我们解决一些复杂的积分问题,如求某个函数的原函数、求曲线下的面积等。
最后是微分方程这一部分。
微分方程是含有未知函数及其导数的方程,通过求解微分方程我们可以得到函数的解析表达式。
在微分方程的求解中,我们需要掌握一些基本的解法,如可分离变量法、一阶线性微分方程的求解方法等。
此外,对于高阶微分方程,我们还需要熟悉齐次线性微分方程、非齐次线性微分方程和常系数线性齐次微分方程的特解等的求解方法。
通过这份思维导图,我们可以更好地了解高等数学大一上的知识点,并掌握相关的考点和解题技巧。
但是仅仅依靠思维导图是不够的,我们还需要辅以大量的练习,不断总结和思考,加深对知识点的理解和运用。
总之,高等数学是一门需要思维和逻辑能力的课程,通过合理的学习方法和不懈的努力,我们一定能够掌握好这门课程。

高等数学a1思维导图第一章
高等数学a1的第一章主要讲的是集合的概念。
集合是一组有相
同特点或共同性质的事物的统称,它是数学研究中非常重要的知识点。
集合由不同元素构成,它们构成了某些特定的结构。
集合几何定义,是指将一组有共同特点的元素看作一个整体,形
成一个集合。
例如,将一组字符看作一个字符串。
集合的概念在其他
学科中也有用,比如组合,统计,数论等等,它们可以分为有序集合、无序集合和有穷集合。
图论研究中也有另一种称为子集的概念。
子集是指集合A中包含
在集合B中的所有元素,它们具有集合A特定的性质,是集合A的一
个子集。
必要性原理也常常用在集合论中,它指出集合A和集合B之间可
能存在一定的依赖关系,如果集合A包含某个元素,则集合B也必定
包含该元素。
本章的内容为我们提供了更深刻的理解集合的概念,帮助我们更
好地应用这种思维方式,更有效地解决问题,从而更好地推动数学的
发展。