2019-2020年八年级上学期四科联赛数学试题.docx

武穴市四科联赛五校联考八年级数学竞赛试题（时间：120分钟满分：100分命题人：石佛寺中学杨植宝）一、选择题。

（每小题5分，共25分）1．若实数a、b、c、d满足a+1=b-2=c+3=d-4，则a、b、c、d这四个实数中最大是（）A．a B．b C．c D．d2．把26个英文字母按规律分成5组，现在还有5个字母D、M、Q、X、Y、Z，请你按原规律补上，其顺序依次为（）①FRPJLQ□②HIO□③NS□④BDKE□⑤V ATYWU□A．QXZMD B．DMQZX C．ZXMDQ D．QXZDM3．如图，直角ABCD中，AD∥BC，AB⊥BC，AD=3，BC=5，将腰DC绕点D的逆时针方向旋转90°至DE，连接AE，则△ADE的面积是（）A．1 B．2 C．3 D．4第3题图第5题图4．一列武广高速列车和一列普通列车的车身长分别400米和600米，它们相向匀速行驶在平行的轨道上，若坐在高速列车上的乘客看见普通列车驶过窗口的时间是3秒，则坐在普通列车上的乘客看见高速列车驶过窗口的时间是（）A．2秒B．3秒C．4秒D．4.5秒5．用若干个相同的小正方体粘成一个立体图形（实心），该立体图形的三视图如图所示，那么所用小正方体的个数为（）A．19个B．20个C．21个D．22个二、填空题。

（每小题5分，共25分）6．有一列数：-2011；-2004。

-1997，-1990，…，它们按一定的规律排列，那么这列数和最小的是前个数。

7．若a、b满足753=+ba，则bas32-=的取值范围是。

8．如图，等边△ABC中，BD=CE，AD与BE交于P，AQ⊥BE，垂足为Q，PD=2，PQ=6，则BE的长为9．已知9619--+++-=axxaxy，如果19＜a＜96，a≤x≤96，则y的最大值为10．某校10名教师带领八年级全体学生乘坐汽车外出参加社会实践活动，要求每辆汽车乘坐的人数相等，起初每辆汽车乘了22人，结果剩下1人未上车；如果有一辆汽车空着开走，那么所有师生正好能平均分乘到其他各车上，已知每辆汽车最多只能容纳32人，则该校八年级有学生名。

初中四科联赛试题及答案一、语文试题1. 请解释下列词语的意思：（1）栩栩如生（2）昙花一现2. 阅读以下古文，回答后面的问题：《出师表》节选先帝创业未半而中道崩殂，今天下三分，益州疲弊，此诚危急存亡之秋也。

然侍卫之臣不懈于内，忠志之士忘身于外者，盖追先帝之殊遇，欲报之于陛下也。

诚宜开张圣听，以光先帝遗德，恢弘志士之气，不宜妄自菲薄，引喻失义，以塞忠谏之路也。

（1）“先帝”指的是谁？（2）“此诚危急存亡之秋也”中的“秋”是什么意思？3. 请写出“草长莺飞二月天，拂堤杨柳醉春烟”的作者和出处。

二、数学试题1. 计算下列表达式的值：（1）\((3x - 2)^2\)（2）\(\frac{3}{4} \div \frac{2}{3}\)2. 解方程：（1）\(2x + 3 = 11\)（2）\(5x - 7 = 8\)3. 一个长方体的长、宽、高分别是10cm、8cm、6cm，求其体积。

三、英语试题1. 根据所给词的适当形式填空：（1）He often ________ (read) books in the library.（2）There ________ (be) many people in the park yesterday.2. 将下列句子翻译成英文：（1）他每天骑自行车上学。

（2）她喜欢在周末去购物。

3. 阅读下面的短文，回答问题：My name is Tom. I am a student. I like playing football. I often play football with my friends on weekends.（1）What is Tom's hobby?（2）When does Tom usually play football?四、科学试题1. 列举三种常见的可再生能源。

2. 解释光合作用的过程。

3. 描述水循环的三个主要阶段。

答案：一、语文试题1. （1）栩栩如生：形容画作或雕塑等艺术作品形象逼真，如同活的一样。

八年级四科联赛2022年秋八年级四科联赛物理试卷欢送你参加四科联赛，细心一点，你一定会取得好成绩!一、选择题：〔将符合题意的答案填入对应的表格中，每题2分，共30分〕2 3 4 5 6 7 8 9 10 11 12 13 14 15 题号 1 答案 1．以下说法错误的选项是 A、放在碟子里的酒精过段时间不见了是蒸发现象 B、雾的形成是液化现象 C、放在啤酒里的冰块越来越小是熔化现象 D、冬天，冰冻的衣服变干是汽化现象２．身体上最接近50mm长度的部位是A、手掌的长度B、手掌的宽度C、大拇指的长度D、小腿的长度３．空气的密度为1.29kg/m3，请你估算一下教室的空气质量最接近以下哪个数值？A、3kg B、30kg C、300kg D、3000kg ４．以下物态变化中，属于液化现象的是A．春天，冰封的河面解冻 B．夏天，剥开的冰棒冒“白气〞 C．秋天，清晨的雾在太阳出来后散去 D．冬天，屋顶的瓦上结了一层霜5．刚从开水中捞出的熟鸡蛋拿在手中不太烫，待蛋壳外表的水分干了之后就很烫了，这是因为 A、蛋的内部温度很高，有热逐渐散发 B、水的温度低，蛋壳温度高 C、蛋壳不善于传热，使手发烫要一段时间D、蛋壳未干时，热水蒸发很快，这时蛋壳温度降低6．如图1，盛酒精的小烧杯漂浮在盛水的大烧杯中。

用酒精灯加热一段时间后，观察到大烧杯中的水只产生了少量气泡，而小烧杯中的酒精已开始沸腾，这个现象可以使我们认识到 A、酒精比水吸热多 B、酒精比水吸热快 C、酒精的沸点比水低 D、酒精的温度比水高7．一只能够容纳1kg水的瓶子，一定能够容纳得下1kg的 A、白酒 B、食用油 C、盐水 D、煤油 8．有甲、乙两金属块，甲的密度是乙的25图1 ，乙的质量是甲的2倍，那么甲的体积是乙的A、0.8倍B、1.25倍C、0.2倍D、5倍 9．人们常说“铁比木头重〞。

这句话确实切含义是 A、铁的密度比木头大 B、铁的质量比木头大 C、铁的体积比木头大 D、铁的重力比木头大10．用不同材料做成体积相同的甲、乙实心小球，在已调好的天平左盘放5个甲球，在右盘放3个乙球，天平恢复平衡，那么甲、乙球的密度之比为A、5∶3B、3∶5C、8∶3D、1∶111．将打气筒的出口封住，向下压活塞时，被封闭在气筒内的气体的质量m，密度ρ的变化是 A、m、ρ都变小 B、m变小、ρ不变 C、m、ρ都不变 D、 m不变、ρ变大 12．一位同学在使用托盘天平时，忘记调节横梁平衡，此时指针偏向中央刻度线的右方，如果用这架天平测物体质量，当天平平衡时A、测量值大于真实值B、测量值小于真实值C、测量值等于真实值D、无法判断13．为铸造金属铸件，事先用密度为ρ1的实心木料制成木模，木模的质量为1.8kg。

2019-2020 年八年级数学竞赛试题含答案_学校姓名成一、 (每小 8 分，共 64 分 )以下每个的四个中，有一个是正确的，将正确答案的英文字母填在后的括号内．1．用 11 到 2006 些自然数依次成下列算式：1112 + 1314， 1516 + 1718 ，1920 + 2122， 2324 + 2526，⋯⋯ 20032004 + 20052006.其中，能被 4整除的算式有() (A)0 个(B) 125 个（ C）250 个（D）499 个2．中的五角星是用螺栓将两端打有孔的 5 根木条接而构成的，它的形状不定．如果用在中木条交叉点打孔加装螺栓的法来达到使其形状定的目的，且所加螺栓尽可能少，那么需要要添加螺栓()(A)1 个(B)2 个（C）3 个（D）4 个3．把度 4 的段分成四小段．若要以四小段构成一个四形，其中每一小段的度足的条件是()11(A) 不大于 1(B) 大于2且小于 1(C) 小于 2(D) 大于4！未定。

且小于 24．如，有一个均匀的片，两面上分写有1、 2，有—个均匀的三棱旋器和一个均匀的四棱旋器，它的面上分写有1、2、3 和 1、2、3、 4.在桌面上同旋三件器物，停下来后，面向桌面的三个数字的奇数的概率是()1111(A) 2(B)3（C）6（D）85．同价格的某种商品在三个商都行了两次提价．甲商第一次提价的百分率a，第二次提价的百分率b；乙商两次提价的百分率都a + b2；丙商第一次提价的百分率 b，第二次提价的百分率a．若 a > b > 0 ，提价最多的商是()(A) 甲(B) 乙(C)丙(D) 不能确定的6．一本册内有24 份卷，共有 426道，每份卷中有25 或 20或 16 ．那么本册中有25 的卷的份数（）(A) 1(B) 2（ C）3（D）47．把一个正方体切成两个方体，如果两者表面乏比l： 2，那么两者体之比（）(A)1：2(B) 1 ：3（ C）1： 5（D） 1：68．有七个大小相同的正方体，每个正方体的六个面上分写有1 到 6 六个整数，并且任意两个相面上的两数之和7．把些正方体如所示一个挨—个地接起来，使相的两个面上的两数之和 8，“※”所在面上的数是()(A)4(B)3（ C）2（D）1二、填空 (每小8 分，共 96 分)9． 算：19972 –19982 +19992 –20002 +⋯ +20052 –20062 =.10．把 (1) 的正方体表面展开成 4 条棱都没有被剪开， 个面是正方形表示 )．(2) ，有—个面的(用字母次是 11．如 ，一个六 形的每个内角都是2. 7、3、 5、 2， 六 形的周 是120 °， 四 的 依.12．小王 置的某种四位密 ，每个密 的各位数字只能是0、 1、 2 或 3，且 0 不能出 在1、 2、3 的后面， 共可以 置 个不同的密 ．13．有 度分 1、2、3、4、5、6、7、 8、 9 ( 位： cm)的 木棒各1 根，利用它 (允 接加 但不允 折断)能 成的周 不同的等 三角形共有种．14．在一个 周上均匀地写了任意四个整数． 定算法是：把每相 两数之和放在 两 数之 ， 然后把原来的四个数抹去， 就算一次操作． 当开始 在 周上所写的四个整数不全是偶数 ，最多只要次操作，就一定能使 周上所得的四个数都 成偶数．15．《 代数学学 》 志2007 年 3 月将改版 《 代学 ·数学周刊》，其徽 是我国古代“弦 ”的 形 ( 示意 )． 可由直角三角形 ABC 点 O 同向 旋 三次 (每次旋90°)而得．因此有“数学 ”的 感．假 中 小正方形的面 1，整个徽(含中 小正方形 )的面 92， AD = 2 ， 徽 的外 周.16．如 ，四 形 ABCD 中， E 、 F 、G 、 H 依次是各 中点，O 是形内一点．若 S四边形AEOH = 3， S四边形BFOE = 4，S四边形CGOF = 5，S 四边形 DHOG =.17． 徒加工某零件，加工1 个零件， 傅比徒弟少用 2. 5 小 ；加工 10 小 ， 傅比徒弟多做 9 个零件． 徒合做3 个零件，需要小 ．x 215x 4 –3x 2 + 518．如果 x 4 + x 2 + 1 =4 ，那么3x 2 =.19．如 ，∠ CAD 和∠ CBD 的平分 相交于点 P ． ∠ CAD 、∠CBD 、∠ C 、∠ D 的度数依次 a 、 b 、 c 、 d ，用 含其中 2 个字母的代数式来表示∠P 的度数：.20．如 ，在每个小正方形1 的网格中取出12 个格点，以 些格点 点的等腰直角三角形的腰 可以是，能得到位置不同的等腰直角三角形 共有个．2008 年从化二中八年级数学竞赛试题参考答案与评分标准一、选择题：（每题 8 分，共 64 分 )题号12345678答案AACCBBCB二、填空题： (每题 8分，共 96 分)-9．–2001510．EFGH (CDHG )11． 20.712． 12113． 1114． 4c + d15． 4816． 4 17．218． 419．220． 1，2， 2 ， 5 ；45．说明：第 10 题写出一个正确结果就给8 分，第 20题第一空共有 4 个值，每填 1 个值得1 分，填错 1 个扣 1 分，第二空 4 分．。

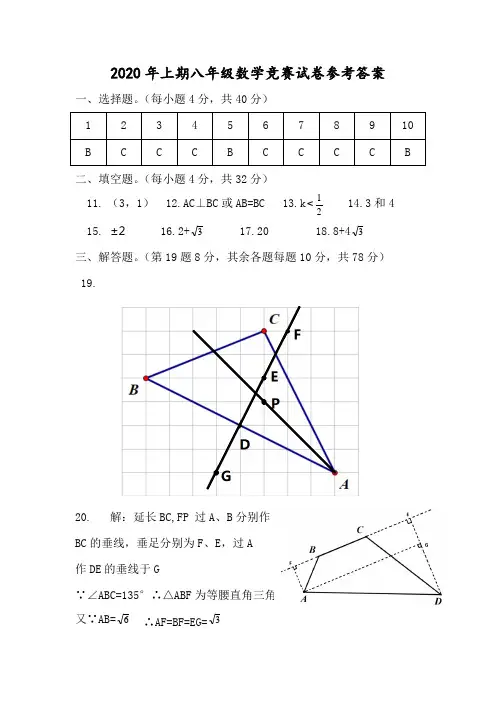
2020年上期八年级数学竞赛试卷参考答案一、选择题。

（每小题4分，共40分）1 2 3 4 5 6 7 8 9 10B C C C B C C C C B二、填空题。

（每小题4分，共32分）114.3和4 11.（3，1） 12.AC⊥BC或AB=BC 13.k<215.±2 16.2+3 17.20 18.8+43三、解答题。

（第19题8分，其余各题每题10分，共78分）19.20.解：延长BC,FP 过A、B分别作BC的垂线，垂足分别为F、E，过A作DE的垂线于G∵∠ABC=135°∴△ABF为等腰直角三角形又∵AB=6∴AF=BF=EG=3∵∠BCD=120° ∴∠CDE=30° ∵CD=6 ∴CE=3,DE=33 ∴AG=EF=8 DG=DE-EG=32∴AB=1927622==+BG AG 21. （1）∵BP ⊥x 轴 ∴P 横=B 横=3∵直线AC 过点A(1,3),C((4,1) ∴直线AC 的解析式为31132+-=x y将P 横=3代入得P 纵=35 ∴P （3，35）（2）S △ABC =S △PAB +S △PBC =37×2×21+37×1×21=2722. ∵,矩形ABCD 中,BC=8,CD=6 ∴BD=10∵△ABE 翻折后为△FBE ∴BF=AB=CD=6,AE=EF,EF ⊥AC ∴DF=BD-BF=4在Rt △DEF 中，设DE=x ，则EF=8-x 42+(8-x)2=x 2 解得x=523.(1)CD=4t ，AE=2t∵∠C=30°,DF ⊥BC ∴DF=21CD=2t∴AE=DF (2)∵AC=60 ∴AD=60-4t 当AD=DE 时，四边形AEFD 为菱形即60-4t=2t 解得t=10(3)当t=215时，三角形DEF 是直角三角形（∠EDF=90°)当t=12时，三角形DEF 是直角三角形（∠DEF=90°)理由如下：当∠EDF=90°时，DE//BC,∴∠ADE=∠C=30° ∴AD=2AE, ∵CD=4t ∴DF=2t=AE ∴AD=4t ， ∴4t+4t=60当t=215时，∠EDF=90°当∠DEF=90°时，DE ⊥EF,∵四边形AEFD 是平行四边形， ∴AD//EF ∴DE ⊥AD ∴△ADE 是直角三角形，∠ADE=90°∵∠A=60° ∴AD=21AE∴AD=AC-CD=60-4t,AE=DF=21CD=2t ∴60-4t=t 解得t=12综上所述，当t=215时，三角形DEF 是直角三角形（∠EDF=90°)当t=12时，三角形DEF 是直角三角形（∠DEF=90°) 24.作BC 的中点N ，连接PN 并延 长与AB 的延长线交于点Q∵∠QBN=∠C=90°,BN=CN,∠BNQ=∠CNP ∴△BNQ ≌△CNP ∴BQ=CP ∴AP=PC+BC=AB+BQ=AQ∵NQ=NP ∴AN 是∠QAP 的角平分线 ∴∠BAP=2∠BAN∵△ABN ≌△AEM ∴∠BAN=∠DAM ∴∠BAP=2∠DAM 25.解：(1)∵点C 在直线x y 3=上，且C 横=1，∴C(1,3)∵一次函数b kx y +=的图象经过A 、C 两点⎩⎨⎧+=+-=b k b k 326解得⎩⎨⎧=-=41b k(2)∴B （4，0）∴S △BOC=21OB ×C 纵=6 ∴21OD ×|C 横|=2 ∴OD=4 ∴D(0,4)或D(0,-4)26. 解（1）设B 市运往C 市X 台，则运往D 市（6-X ）台，A 市运往C 市（10-X ）台，运往D 市（X+2)台，由题意得：)6(53)2(8)10(4x x x x y -++++-=即862+=x y⎪⎪⎩⎪⎪⎨⎧≥+≥-≥-≥02010060x x x x 解得60≤≤x （2）∵总费用超过90万∴2x+86≤90 解得x ≤2 结合第（1）小题，得20≤≤x ∵x 取整数 ∴一共有三种方案 （3）∵在862+=x y 中，K=2>0∴y 随x 的增大而增大 ∴当X=0时，y 最小=86万元。

2019-2020年八年级上学期第一次质量调研数学试题一、选择题：（本题共8个小题，每小题3分，共24分．在每小题给出的四个选项中，恰有一项是符合题目要求的，请将正确选择项前的字母代号填入下表）题号 1 2 3 4 5 6 7 8答案1.两个全等图形中可以不同的是A.位置B.长度C.角度D.面积2. 如图，已知△ABC，则下列甲、乙、丙三个三角形中和△ABC全等的图形是A．甲乙 B．甲丙 C．乙丙 D．乙3．尺规作图作∠AOB的平分线方法如下：以O为圆心，任意长为半径画弧交OA，OB于C，D，再分别以点C，D为圆心，以大于CD长为半径画弧，两弧交于点P，作射线OP由作法得△OCP≌△ODP的根据是A．SSS B.SAS C.ASA D.AAS4．下列各组条件中，能判定△ABC≌△DEF的是A．AB=DE，BC=EF，∠A=∠DB．∠A=∠D，∠C=∠F，AC=EFC．AB=DE，BC=EF，△ABC的周长=△DEF的周长D．∠A=∠D，∠B=∠E，∠C=∠F5．如图，有一块三角形的玻璃，不小心掉在地上打成三块，现要到玻璃店重新划一块与原来形状、大小一样的玻璃，只需带第块到玻璃店去A．① B．② C．③ D．②或③6．如图，已知AD平分∠BAC，AB=AC，则此图中全等三角形有A. 2对B.3 对C.4对D.5对AFBCDMEN 12BAC第13题图第5题 第6题 第7题7．如图，∠E =∠F =90°，∠B =∠C ，AE =AF ，给出下列结论：①∠1=∠2；②BE =CF ；③△ACN ≌△ABM ；④CD =DN ，其中正确的结论有A.1个B.2个C.3个D.4个8．△ABC 是格点三角形（顶点在网格线的交点），则在图中能够作出与△ABC 全等且有一条公共边的格点三角形（不含△ABC ）的个数是A.1个B.2个C.3个D.4个 二、填空题（本题共10个小题，每小题3分，共30分．）9．如图，如果△ABC ≌△DEF ，△DEF 周长是32cm ，DE=9cm ，EF=13cm ，则AC= cm ．10．如图，△ABC ≌△AEC ，∠B =30°，∠ACB =85°，∠EAC= °．11．在△ABC 和△DEF 中，已知AB=DE ，AC=DF ，要证明△ABC ≌DEF ，所缺的一个条件是_________（填符合条件的一个即可）．第10题 第12题12．如图，已知AB ∥CF ，E 为DF 的中点，若AB =9㎝，CF =5㎝，则BD = ㎝. 13．如图为6个边长相等的正方形的组合图形，则∠1+∠2+∠3= °． 14．工人师傅在安装木制门框时，为防止变形常常像图中所示，钉上两条斜拉的木条，这样做的原理是根据三角形的 性．15．如图，点P 是∠BAC 的平分线AD 上一点，PE ⊥AC 于点E ．已知PE =3，则点P 到AB 的距离是16．如图，有两个长度相同的滑梯（即BC =EF ），左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等，则∠ABC +∠DFE = 度．F EDAB CD E B AC F① ② ③17．如图，在△ABC中，AB=AC，AD=AE，∠BAC=∠DAE，∠1=25°，∠2=30°，则∠3= ．18．如图，已知在△ABC中，∠A=90°，AB=AC，CD平分∠ACB，DE⊥BC于E，若BC=15cm，则△DEB的周长为cm．三.解答题：（本题共10个小题，共66分）19.（本题8分）已知∠AOB，用直尺和圆规作图：（1）做∠AOB的平分线(2)过∠AOB边OA上一点P分别作边OA、OB的垂线。

2019-2020年八年级上学期期初数学试卷一、填空题（每题3分，满分30分）1．的算术平方根是，=．2．的平方根等于它本身，的立方根等于它本身，的算术平方根等于它本身．3．已知线段AB=3，AB∥x轴，若点A坐标为（1，2），则B点坐标为．4．以为解的一个二元一次方程是．5．若方程x﹣2y+3z=0，且当x=1时，y=2，则z=．6．如图所示，如果2∠3=3∠1，则∠2=，∠3=，∠4=．7．如图，BC⊥AB，CB=6cm，AB=8cm，AC=10cm，那么点B到AC的距离是，点A到BC的距离是，点C到AB的距离是．8．已知，如图，AB∥CD，则∠α、∠β、∠γ之间的关系为．9．如图所示的象棋盘上，若帅位于点（1，﹣2）上，相位于点（3，﹣2）上，则炮位于点．10．方程2x+y=8在正整数范围内的解是．二、单项选择题（每题3分，满分30分）11．﹣8的立方根与4的平方根的和是（）A．0 B．0或4 C．4 D．0或﹣412．如图，在数轴上1，的对应点分别是点A和点B，A是线段BC的中点，则点C所表示的数是（）A．B．C．D．13．如图，直线a，b被直线c所截，现给出下列四个条件，其中不能判定a∥b的条件的是（）A．∠1=∠5 B．∠2+∠7=180°C．∠2+∠3=180°D．∠2=∠8．14．若5x﹣6y=0，且xy≠0，则的值等于（）A．B．C．1 D．﹣115．若y轴上的点P到x轴的距离为3，则点P的坐标是（）A．（3，0）B．（0，3）C．（3，0）或（﹣3，0）D．（0，3）或（0，﹣3）16．已知点A（2，﹣2），如果点A关于x轴的对称点是B，点B关于原点的对称点是C，那么C点的坐标是（）A．（2，2）B．（﹣2，2）C．（﹣1，﹣1）D．（﹣2，﹣2）17．已知（a﹣2）2+|b+3|=0，则P（﹣a，﹣b）的坐标为（）A．（2，3）B．（2，﹣3）C．（﹣2，3）D．（﹣2，﹣3）18．点M（a，a﹣1）不可能在（）A．第一象限B．第二象限C．第三象限D．第四象限19．下列判断正确的是（）A．从直线外一点到已知直线的垂线段叫做这点到已知直线的距离B．过直线外一点画已知直线的垂线，垂线的长度就是这点到已知直线的距离C．画出已知直线外一点到已知直线的距离D．连接直线外一点与直线上各点的所有线段中垂线段最短20．下列方程组中，是二元一次方程组的是（）A．B．C．D．三、解答题（满分60分）21．用适当方法解下列方程组（1）（2）．22．已知，求y x的平方根．23．已知实数a、b在数轴上的位置如图所示：试化简：﹣|a+b|．24．如果a+3和2a﹣15是一个正数的平方根，求a的值及这个数．25．如图，把△ABC的点A平移到点A1（﹣2，4），（1）画出，并写出△A1B1C1两点的坐标．（2）求出△ABC的面积．26．二元一次方程组的解x，y的值相等，求k．27．如图，已知AB∥CD，∠B=60°，CM平分∠BCE，∠MCN=90°，求∠DCN的度数．28．小亮跟爸爸于9月和10月初两次到超市购买食品．9月初：买6袋牛奶，12个面包，用30元．10月初：国庆酬宾，一律七五折优惠，比上次多买了4袋牛奶和3个面包．根据打折前后花30元所购买的物品数量，你能求出打折前牛奶和面包的单价各是多少吗？xx学年黑龙江省齐齐哈尔市龙江县八年级（上）期初数学试卷参考答案与试题解析一、填空题（每题3分，满分30分）1．的算术平方根是3，=．考点：立方根；算术平方根．分析：求出=9，即可得出的算术平方根，求出=，再求出立方根即可．解答：解：∵=9，∴的算术平方根是3，==，故答案为：3，．点评：本题考查了算术平方根和立方根的应用，主要考查学生的计算能力．2．0的平方根等于它本身，1或﹣1或0的立方根等于它本身，0或1的算术平方根等于它本身．考点：立方根；平方根；算术平方根．分析：根据平方根、立方根、算式平方根的定义进行判断即可．解答：解：0的平方根是0，等于它本身，0和±的立方根等于它本身，0和1的算式平方根等于它本身，故答案为：0；1或﹣1或0；0或1．点评：本题考查了平方根、立方根、算式平方根的定义的应用，主要考查学生的理解能力和计算能力．3．已知线段AB=3，AB∥x轴，若点A坐标为（1，2），则B点坐标为（4，2）或（﹣2，2）．考点：坐标与图形性质．专题：分类讨论．分析：AB∥x轴，说明A，B的纵坐标相等为2，再根据两点之间的距离公式求解即可．解答：解：∵AB∥x轴，点A坐标为（1，2），∴A，B的纵坐标相等为2，设点B的横坐标为x，则有AB=|x﹣1|=3，解得：x=4或﹣2，∴点B的坐标为（4，2）或（﹣2，2）．故本题答案为：（4，2）或（﹣2，2）．点评：本题主要考查了平行于x轴的直线上的点的纵坐标都相等．注意所求的点的位置的两种情况．4．以为解的一个二元一次方程是x+y=12．考点：二元一次方程的解．专题：开放型．分析：利用方程的解构造一个等式，然后将数值换成未知数即可．解答：解：例如1×5+1×7=12；将数字换为未知数，得x+y=12．答案不唯一．点评：此题是解二元一次方程的逆过程，是结论开放性题目．二元一次方程是不定个方程，一个二元一次方程可以有无数组解，一组解也可以构造无数个二元一次方程．不定方程的定义：所谓不定方程是指解的范围为整数、正整数、有理数或代数整数的方程或方程组，其未知数的个数通常多于方程的个数．5．若方程x﹣2y+3z=0，且当x=1时，y=2，则z=1．考点：解三元一次方程组．专题：计算题．分析：将x与y的值代入方程计算即可求出z的值．解答：解：将x=1，y=2代入方程得：1﹣4+3z=0，解得：z=1，故答案为：1．点评：此题考查了解三元一次方程组，熟练掌握运算法则是解本题的关键．6．如图所示，如果2∠3=3∠1，则∠2=108°，∠3=108°，∠4=72°．考点：对顶角、邻补角．专题：计算题．分析：根据邻补角的和等于180°可得∠1+∠3=180°，然后求出∠1与∠3的度数，再根据对顶角相等解答．解答：解：∵2∠3=3∠1，∠1+∠3=180°（邻补角定义），∴∠1=72°，∠3=108°，∴∠2=∠3=108°（对顶角相等），∠4=∠1=72°（对顶角相等）．故答案为：108°，108°，72°．点评：本题考查了对顶角相等，邻补角的和等于180°，求出∠1与∠3的度数是解题的关键．7．如图，BC⊥AB，CB=6cm，AB=8cm，AC=10cm，那么点B到AC的距离是 4.8cm，点A到BC的距离是8cm，点C到AB的距离是6cm．考点：点到直线的距离．分析：过点B作BD⊥AC于点D，则线段BD的长即为点B到AC的距离，再根据三角形的面积公式求出BD的长；再根据点到直线距离的定义即可得出结论．解答：解：过点B作BD⊥AC于点D，则线段BD的长即为点B到AC的距离，∵BC⊥AC，CB=6cm，AB=8cm，AC=10cm，∴BD=6×8÷10=4.8cm，点A到BC的距离是8cm，点C到AB的距离是6cm．故答案为：4.8cm，8cm，6cm．点评：本题考查了点到直线的距离，是基础题，熟记点到直线的距离的定义是解题的关键．8．已知，如图，AB∥CD，则∠α、∠β、∠γ之间的关系为∠α+∠β﹣∠γ=180°．考点：平行线的性质．分析：过E作EF∥AB∥CD，由平行线的质可得∠α+∠AEF=180°，∠FED=∠γ，由∠β=∠AEF+∠FED即可得∠α、∠β、∠γ之间的关系．解答：解：过点E作EF∥AB∴∠α+∠AEF=180°（两直线平行，同旁内角互补）∵AB∥CD（已知）∴EF∥CD．∴∠FED=∠EDC（两直线平行，内错角相等）∵∠β=∠AEF+∠FED又∵∠γ=∠EDC（已知）∴∠α+∠β﹣∠γ=180°．点评：本题考查了平行线的性质，正确作出辅助线是解题的关键．9．如图所示的象棋盘上，若帅位于点（1，﹣2）上，相位于点（3，﹣2）上，则炮位于点（﹣2，1）．考点：坐标确定位置．专题：应用题．分析：以“帅”位于点（1，﹣2）为基准点，再根据““右加左减，上加下减”来确定坐标即可．解答：解：以“帅”位于点（1，﹣2）为基准点，则“炮”位于点（1﹣3，﹣2+3），即为（﹣2，1）．故答案为（﹣2，1）．点评：本题考查了类比点的坐标及学生解决实际问题的能力和阅读理解能力，解决此类问题需要先确定原点的位置，再求未知点的位置．或者直接利用坐标系中的移动法则“右加左减，上加下减”来确定坐标，难度适中．10．方程2x+y=8在正整数范围内的解是；；．考点：解二元一次方程．专题：计算题．分析：将x看做已知数求出y，即可确定出正整数解．解答：解：方程2x+y=8，解得：y=8﹣2x，当x=1时，y=6；当x=2时，y=4；当x=3时，y=2，则方程的正整数解为；；．故答案为：；；点评：此题考查了解二元一次方程，解题的关键是将x看做已知数求出y．二、单项选择题（每题3分，满分30分）11．﹣8的立方根与4的平方根的和是（）A．0 B．0或4 C．4 D．0或﹣4考点：立方根；平方根．分析：根据立方根的定义求出﹣8的立方根，根据平方根的定义求出4的平方根，然后即可解决问题．解答：解：∵﹣8的立方根为﹣2，4的平方根为±2，∴﹣8的立方根与4的平方根的和是0或﹣4．故选D．点评：本题考查了平方根和立方根的概念．注意一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根．立方根的性质：一个正数的立方根式正数，一个负数的立方根是负数，0的立方根式0．12．如图，在数轴上1，的对应点分别是点A和点B，A是线段BC的中点，则点C所表示的数是（）A．B．C．D．考点：实数与数轴．分析：首先根据数轴上1，的对应点分别是点A和点B可以求出线段AB的长度，然后根据中点的性质即可解答．解答：解：∵数轴上1，的对应点分别是点A和点B，∴AB=﹣1，∵A是线段BC的中点，∴CA=AB，∴点C的坐标为：1﹣（﹣1）=2﹣．故选A．点评：本题考查的知识点为：求数轴上两点间的距离就让右边的数减去左边的数．知道两点间的距离，求较小的数，就用较大的数减去两点间的距离．13．如图，直线a，b被直线c所截，现给出下列四个条件，其中不能判定a∥b的条件的是（）A．∠1=∠5 B．∠2+∠7=180°C．∠2+∠3=180°D．∠2=∠8．考点：平行线的判定．分析：结合图形分析两角的位置关系，根据平行线的判定方法判断．解答：解：A、若∠1=∠5时，则根据“同位角相等，两直线平行”可以判定a∥b．故本选项错误；B、若∠2+∠7=180°时，则∠4+∠5=180°，则由“同旁内角互补，两直线平行”可以判定a∥b．故本选项错误；C、∠2与∠3互为补角，不能根据∠2+∠3=180°判定a∥b．故本选项正确；D、若∠2=∠8时，则∠4=∠8，根据“同位角相等，两直线平行”可以判定a∥b．故本选项错误；故选：C．点评：本题考查了平行线的判定．解答此类要判定两直线平行的题，可围绕截线找同位角、内错角和同旁内角．本题是一道探索性条件开放型题目，能有效地培养“执果索因”的思维方式与能力．14．若5x﹣6y=0，且xy≠0，则的值等于（）A．B．C．1 D．﹣1考点：二元一次方程的解．分析：首先得出x=y，进而代入原式求出即可．解答：解：∵5x﹣6y=0，∴x=y，∴==．故选：A．点评：此题主要考查了二元一次方程的解，正确转化x与y的关系是解题关键．15．若y轴上的点P到x轴的距离为3，则点P的坐标是（）A．（3，0）B．（0，3）C．（3，0）或（﹣3，0）D．（0，3）或（0，﹣3）考点：点的坐标．分析：由点在y轴上首先确定点P的横坐标为0，再根据点P到x轴的距离为3，确定P点的纵坐标，要注意考虑两种情况，可能在原点的上方，也可能在原点的下方．解答：解：∵y轴上的点P，∴P点的横坐标为0，又∵点P到x轴的距离为3，∴P点的纵坐标为±3，所以点P的坐标为（0，3）或（0，﹣3）．故选：D．点评：此题考查了由点到坐标轴的距离确定点的坐标，特别对于点在坐标轴上的特殊情况，点到坐标轴的距离要分两种情况考虑点的坐标．16．已知点A（2，﹣2），如果点A关于x轴的对称点是B，点B关于原点的对称点是C，那么C点的坐标是（）A．（2，2）B．（﹣2，2）C．（﹣1，﹣1）D．（﹣2，﹣2）考点：关于原点对称的点的坐标；关于x轴、y轴对称的点的坐标．专题：计算题．分析：平面直角坐标系中任意一点P（x，y），关于x轴的对称点的坐标是（x，﹣y），关于原点的对称点是（﹣x，﹣y）．解答：解：A关于x轴的对称点是B的坐标是（2，2），∵点B关于原点的对称点是C，∴C点的坐标是（﹣2，﹣2）．故选D．点评：记忆方法是结合平面直角坐标系的图形记忆，另一种记忆方法是记住：关于横轴的对称点，横坐标不变，纵坐标变成相反数；关于纵轴的对称点，纵坐标不变，横坐标变成相反数；关于原点的对称点，横纵坐标都变成相反数．17．已知（a﹣2）2+|b+3|=0，则P（﹣a，﹣b）的坐标为（）A．（2，3）B．（2，﹣3）C．（﹣2，3）D．（﹣2，﹣3）考点：点的坐标；非负数的性质：绝对值；非负数的性质：偶次方．分析：根据非负数的性质，求出a，b的数值，可得P（﹣a，﹣b）的坐标．解答：解：∵（a﹣2）2+|b+3|=0，∴（a﹣2）2=0，|b+3|=0，解得a=2，b=﹣3，∴P（﹣a，﹣b）的坐标为（﹣2，3）．故选C．点评：本题主要考查了平面直角坐标系中各个象限的点的坐标的符号特点，以及非负数的性质，解答此题的关键是熟记平面直角坐标系中各个象限内点的坐标符号．18．点M（a，a﹣1）不可能在（）A．第一象限B．第二象限C．第三象限D．第四象限考点：点的坐标．分析：分a﹣1＞0和a﹣1＜0两种情况讨论，即可得到a的取值范围，进而求出M所在的象限．解答：解：当a﹣1＞0时，a＞1，点M可能在第一象限；当a﹣1＜0时，a＜1，点M在第三象限或第四象限；所以点M不可能在第二象限．故选B．点评：本题考查象限点的坐标的符号特征，根据第三象限为（﹣，﹣）第二象限为（﹣，+），判断点M的符号不可能为（﹣，+）．记住横坐标相同的点在一四象限或二三象限是关键．19．下列判断正确的是（）A．从直线外一点到已知直线的垂线段叫做这点到已知直线的距离B．过直线外一点画已知直线的垂线，垂线的长度就是这点到已知直线的距离C．画出已知直线外一点到已知直线的距离D．连接直线外一点与直线上各点的所有线段中垂线段最短考点：点到直线的距离；垂线段最短．分析：根据点到直线的距离的含义及垂线的性质进行判断即可．解答：解：A应该是：从直线外一点到已知直线的垂线段的长度叫做这点到已知直线的距离，故A错误；B应该是：垂线是一条射线不是线段，点到已知直线的距离应该是垂线段的长度，故B错误；C应该说：画出已知直线外一点到已知直线的垂线，故C错误；D描述的是垂线的性质，故D正确；故选D．点评：垂线段是一个图形，它是垂线的一部分，而点到直线的距离是一个数量，不是图形．20．下列方程组中，是二元一次方程组的是（）A．B．C．D．考点：二元一次方程组的定义．分析：二元一次方程的定义：含有两个未知数，并且未知数的项的最高次数是1的方程叫二元一次方程．二元一次方程组的定义：由两个二元一次方程组成的方程组叫二元一次方程组．解答：解：根据定义可以判断A、满足要求；B、有a，b，c，是三元方程；C、有x2，是二次方程；D、有x2，是二次方程．故选A．点评：二元一次方程组的三个必需条件：（1）含有两个未知数；（2）每个含未知数的项次数为1；（3）每个方程都是整式方程．三、解答题（满分60分）21．用适当方法解下列方程组（1）（2）．考点：解二元一次方程组．专题：计算题．分析：（1）方程组利用加减消元法求出解即可；（2）方程组利用加减消元法求出解即可．解答：解：（1），①+②得：3x=6，即x=2，将x=2代入②得：y=﹣1，则方程组的解为；（2），①+②×3得：7x=20，即x=，将x=代入①得：y=﹣，则方程组的解为．点评：此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．22．已知，求y x的平方根．考点：二次根式有意义的条件．专题：计算题．分析：本题主要考查自变量的取值范围，根据二次根式的性质，被开方数大于等于0，列不等式组求解．解答：解：依题意，得，解得x=2，所以y=3，所以y x=9，9的平方根是±3，即y x的平方根为±3．点评：本题的关键是被开方数为非负数，平方根的概念．23．已知实数a、b在数轴上的位置如图所示：试化简：﹣|a+b|．考点：二次根式的性质与化简；实数与数轴．分析：利用绝对值的性质以及绝对值的性质分别化简求出即可．解答：解：由数轴可得出：a﹣b＞0，a+b＜0，故﹣|a+b|=a﹣b+（a+b）=2a．点评：此题主要考查了二次根式是的化简，得出各项符号是解题关键．24．如果a+3和2a﹣15是一个正数的平方根，求a的值及这个数．考点：平方根．分析：根据题意的方程a+3+2a﹣15=0，求出a，求出a+3，即可得出答案．解答：解：∵a+3和2a﹣15是一个正数的平方根，∴a+3+2a﹣15=0，∴a=4，∴a+3=7，∴这个数是49．点评：本题考查了对平方根定义的应用，注意：一个正数有两个平方根，它们互为相反数．25．如图，把△ABC的点A平移到点A1（﹣2，4），（1）画出，并写出△A1B1C1两点的坐标．（2）求出△ABC的面积．考点：作图-平移变换．专题：作图题．分析：（1）根据网格结构找出点A、B、C的对应点A1、B1、C1的位置，然后顺次连接即可，再根据平面直角坐标系写出各点的坐标；（2）利用△ABC所在的矩形的面积减去四周三个小直角三角形的面积，列式计算即可得解．解答：25、（1）△A1B1C1如图所示；B1（﹣3，2），C1（﹣5，3）；（2）△ABC的面积=3×2﹣×1×3﹣×1×2﹣×1×2=6﹣1.5﹣1﹣1=2.5．点评：本题考查了利用平移变换作图，熟练掌握网格结构准确找出对应点的位置是解题的关键．26．二元一次方程组的解x，y的值相等，求k．考点：解三元一次方程组．分析：由于x=y，故把x=y代入第一个方程中，求得x的值，再代入第二个方程即可求得k 的值．解答：解：由题意可知x=y，∴4x+3y=7可化为4x+3x=7，∴x=1，y=1．将x=1，y=1代入kx+（k﹣1）y=3中得：k+k﹣1=3，∴k=2点评：由两个未知数的特殊关系，可将一个未知数用含另一个未知数的代数式代替，化“二元”为“一元”，从而求得两未知数的值．27．如图，已知AB∥CD，∠B=60°，CM平分∠BCE，∠MCN=90°，求∠DCN的度数．考点：平行线的性质．分析：根据平行线的性质求出∠BCD和∠BCE，根据角平分线定义求出∠ECM，即可求出答案．解答：解：∵AB∥CD，∴∠B+∠BCE=180°，∠BCD=∠B，∵∠B=60°，∴∠BCE=120°，∠BCD=60°，∵CM平分∠BCE，∴∠ECM=∠BCE=60°，∵∠MCN=90°，∴∠DCN=180°﹣60°﹣90°=30°．点评：本题考查了平行线的性质，角平分线定义的应用，解此题的关键是求出∠ECM的度数．28．小亮跟爸爸于9月和10月初两次到超市购买食品．9月初：买6袋牛奶，12个面包，用30元．10月初：国庆酬宾，一律七五折优惠，比上次多买了4袋牛奶和3个面包．根据打折前后花30元所购买的物品数量，你能求出打折前牛奶和面包的单价各是多少吗？考点：二元一次方程组的应用．可编辑修改分析：设打折前牛奶的单价是x元，面包的单价是y元．由题意得两个等量关系：①打折前买6袋牛奶+12个面包=30元．②打折后买106袋牛奶+15个面包=30元．由等量关系列出方程即可解决．解答：解：设打折前牛奶的单价是x元，面包的单价是y元．由题意得：解得：．答：设打折前牛奶的单价是1元，面包的单价是2元．点评：此题考查二元一次方程组的应用，关键是由题意找等量关系列出方程．.希望能帮到您，欢迎下载。

2019-2020年初中数学联赛初赛试卷及答案四、（本题满分25分）如图，AB 是⊙o 的直径，AB=d ，过A 作⊙o 的切线并在其上取一点C ，使AC=AB ，连结OC 叫⊙o 于点D ，BD 的延长线交AC 于E ，求AE 的长。

五、（本题满分25分）设x = a+b －c ,y=a+c －b ,z= b+c －a ,其中a 、b 、c 是待定的质数，如果x 2试求积abc 的所有可能的值。

B A OE D C参考解答及评分标准一、选择题（每小题7分，共计42分）1、D2、B3、C4、A5、C6、C二、填空题（每小题7分，共计28分）3、45°4、12 1、a2－2 2、2三、解：∵原点是线段AB 的中点⇒点A 和点B 关于原点对称设点A 的坐标为（a ，b ），则点B 的坐标为（―a ，―b ）……5分又 A 、B 是抛物线上的点，分别将它们的坐标代入抛物线解析式，得：22242242b a a b a a ⎧=+-⎪⎨-=--⎪⎩ …………………………10分 解之得： a = 1 , b = 4 或者a = －1 ,b = －4…………………15分 故 A 为（1，4），B 为（-1，-4） 或者 A （-1，-4），B （1，4）.……20分 四、解：如图连结AD ，则∠1=∠2=∠3=∠4∴ΔCDE ∽ΔCAD∴T 1T 122-+⋅CD CADE AD =① ………………5分 又∵ΔADE ∽ΔBDA ∴AE ABDE AD=② ………………10分 由①、②及AB=AC ，可得AE=CD …………15分 又由ΔCDE ∽ΔCAD 可得CD CE CA CD=，即AE 2=CD 2=C E ·CA …………20分 设AE=x ，则CE=d －x ，于是 x 2=d(d －x) 即有AE = x =1d 2（负值已舍去） ……………………25分五、解：∵a+b －c=x, a+c －b=y, b+c －a =z ,∴a =1(x y)2+, b=1(x z)2+, c=1(y z)2+ …………………5分 又∵ y=x 2 , 故 a=21(x x )2+---(1); b=1(x z)2+-----(2) BA O EDC 43 2 1c=21(x z)2+----(3)∴∵x 是整数，得1+8a=T 2，其中T 是正奇数。

四科联赛数学试卷一、填空题：(每小题3分,共30分) 1、若分式11--x x 的值为零，则X 的值为__________.2、已知一个样本：1、3、5、X 、2的平均数是3，则这个样本的方差是___________. 3、如果点A(2、3)关于y 轴的对称点正好落在反比例函数xky =的图象上，则这个反比例函数的解析式是_______________.4、ΔABC 中有两边长为2、3，则第三边长为_____________时，ΔABC 为直角三角形。

5、如图，梯形ABCD 中，AD ∥BC ，AB=CD, 若AD=4, BC=8, ∠B=60°, 则梯形ABCD 的面积为___________.6、如图，P 是正方形ABCD 内一点，将ΔABP 绕B 顺时针旋转90°到ΔCBP ′位置，若BP=a ，则PP ′=_____________.7、菱形ABCD 的对角线的长分别为2和5，P 是对角线AC 上任一点 （点P 不与点A 、C 重合），且PE ∥BC 交AB 于E ，PF ∥CD 交AD 于F ，则阴影部分的面积是_______8. 当5个整数从小到大排列，则中位数是4，如果这5个数的唯一众数是6，则这5个整数可能的最大和是（ ）A 、21B 、22C 、23D 、249. 如图，DE 是△ABC 的中位线，M 是DE 的中点，CM 的延长线交AB 于点N ，则S △DMN ∶S 四边形ANME 等于（ ）A 、1∶5B 、1∶4C 、2∶5D 、2∶7二、选择题：(每小题3分，共18分)11、在某城市，80%的家庭年收入不少于2.5万元，下面一定不少于2.5万元的是( ) A 、年收入的平均数 B 、年收入的众数C 、年收入的平均数和众数 D 、年收入的中位数 12、正比例函数y=2kx 与反比例函数y= 在同一坐标系中的图象不可能的是( )13、平行四边形的周长为25cm, 两对角边的距离分别为2cm 和3cm ,则这个平行四边形的面积为( ) cm 2A ：15B ：25C ：30D ：5014、15、如图，△OAP 、△ABQ 均为等腰直角三角形，点P 、Q 在函数)0(4>=x xy 的图像上，直角顶点A 、B 均在x 轴上，则点B 的坐标为（ ）16、如图，矩形ABCD 中，AB=8, BC=6, E 、F 是AC 上的三等分点，则ΔBEF 的面积为( ) A 、8 B 、12 C 、16 D 、24三、(17题6分，18题7分，19题7分，计20分 )18、（10分）（2006年广西柳州、北海市）任意剪一个三角形纸片，如图9中的△ABC ，设它的一个锐角为∠A ，首先利用对折的方法得到高AN ，然后按图中所示的方法分别将含有∠B 、∠C 的部分向里折，找出AB 、AC 的中点D 、E ，同时得到两条折痕DF 、EG ，分别沿折痕DF 、EG 剪下图中的三角形①、②，并按图中箭头所指的方向分别旋转180°． (1)你能拼成一个什么样的四边形？并说明你的理由； (2)请你利用这个图形，证明三角形的面积公式：S =21底×高．19、在一次捐款活动中，小华对八年级( 1)、( 2)班捐款进行了统计，获得的信息如下： 信息一：( 1)班共捐款300元，(2)班共捐款232元。