密度公式的应用与测量物质的

密度的计算方法密度是物质的质量和体积的比值，通常用来描述物质的紧密程度。

在科学实验和工程领域中，密度的计算是非常重要的，下面将介绍几种常见的密度计算方法。

首先，最常见的密度计算方法是利用物质的质量和体积来计算。

其计算公式为，密度=物质的质量/物质的体积。

在实际操作中，可以先测量物质的质量，然后再测量物质的体积，最后将两个数值代入计算公式中，即可得到物质的密度。

其次，对于不规则形状的物体，可以利用水排量法来计算其密度。

首先，需要准备一个容器，并注满水。

然后，将不规则形状的物体轻轻放入容器中，记录下水位上升的高度。

接着，将物体取出，再次记录水位的高度。

最后，根据水位上升的高度差，可以计算出物体的体积。

将物体的质量和体积代入密度的计算公式中，即可得到物体的密度。

此外，对于气体的密度计算，可以利用理想气体状态方程来进行。

理想气体状态方程表示为PV=nRT，其中P表示气体的压强，V表示气体的体积，n表示气体的摩尔数，R为气体常数，T表示气体的温度。

通过测量气体的压强、体积和温度，可以利用理想气体状态方程来计算气体的密度。

最后，对于液体的密度计算，可以利用比重瓶来进行。

比重瓶是一种专门用来测量液体密度的仪器。

首先，需要将比重瓶干净地注满液体，并记录下比重瓶的质量。

然后，将比重瓶中的液体倒出，再次记录比重瓶的质量。

根据液体的质量和比重瓶的容积，可以计算出液体的密度。

综上所述，密度的计算方法有多种多样，可以根据不同的物质形态和实验条件来选择合适的计算方法。

在进行密度计算时，需要注意测量的准确性和数据的可靠性，以确保得到准确的密度数值。

密度的计算方法对于科学研究和工程实践具有重要意义，希望本文介绍的内容能够对大家有所帮助。

密度及应用的原理密度是物质的重量与其体积的比值，常用符号为ρ（读作“rho”）。

它定义为单位体积内物质的质量，单位通常为克/立方厘米或千克/立方米。

密度是物质的一种特性，不同物质具有不同的密度。

密度的大小与物质的组成、结构和温度有关。

密度的计算公式为：密度= 物质的质量/ 物质的体积在实际应用中，密度是一个重要的物理量，因为它与物质的组成和性质密切相关，可以用来表征物质的物理状态、纯度、浓度等。

密度的原理可以从两个角度来解释。

从微观角度来看，物质是由原子、分子或离子等微粒组成的，它们之间存在着相互作用力。

密度实际上是这些微粒的平均距离的一种表示。

如果物质的微粒之间距离较近，那么单位体积内的微粒数目就较大，质量也就较大，密度也就较大。

反之，如果微粒之间距离较远，那么单位体积内的微粒数目就较少，质量也就较小，密度也就较小。

因此，密度可以反映物质内微观粒子的排列状况。

从宏观角度来看，密度也可以理解为物质的“集中程度”。

对于相同质量的物质来说，当体积较小时，密度较大；当体积较大时，密度较小。

这是因为单位体积内的物质质量相同，但在小体积内，物质分布得更为集中，所以密度较大；在大体积内，物质分布得相对较稀疏，所以密度较小。

在中学物理中，我们学过一个简单的实验，用铁块和木块比较，相同质量的铁块要比木块小得多，因为铁块的密度远大于木块的密度。

密度的应用非常广泛，下面我将介绍几个常见的应用。

首先，密度可以用来鉴别物质的性质。

不同物质的密度是不同的，因此通过测量物质的密度可以实现对物质的鉴别和分类。

例如，水的密度为1克/立方厘米，当我们将一块物质放入水中，如果它的密度小于1克/立方厘米，就会浮在水面上，如果它的密度大于1克/立方厘米，就会沉到水底。

这个原理被广泛应用于实验室中的密度梯度离心法等分离技术。

其次，密度可以用来判断物体的纯度。

以金银为例，金的密度约为19克/立方厘米，而银的密度约为10克/立方厘米，两者混合后的密度会介于两者之间。

密度分析的原理密度分析是一种用于分析物质的密度的方法，密度是指单位体积内所包含的质量。

它是物质的重量与占据的空间相关联的量，是一个衡量物质紧凑程度的物理量。

在实际应用中，密度分析是非常重要的，因为可以帮助确定物质的组成、纯度和特性，从而对物质进行鉴定、分离和提纯。

密度分析的原理基于物质的密度公式，即密度（ρ）等于物质的质量（m）除以物质的体积（V）：ρ= m/V。

因此，密度分析通常包括两个基本步骤：测量物质的质量和测量物质的体积。

这两个步骤可以通过不同的方法和工具来实现，例如称量、容积测量、流变仪等。

在测量物质的质量时，通常会使用天平或电子称等工具来准确测量物质的质量。

在实验中，可以把待测物质置于容器上，然后使用天平或电子称来测量物质的质量。

需要注意的是，为了得到准确的结果，应该在天平或电子称上进行零位校准，并使用适当的称量方法，以避免称量误差对结果的影响。

在测量物质的体积时，可以使用容积瓶、密度瓶等容器来准确测量物质的体积。

而对于非规则形状的物质，可以使用排水法或浸水法等方法来测量其体积。

排水法是通过将待测物质放入水中，观察水面上升的高度，并结合容器的刻度来计算物质的体积；而浸水法则是将待测物质完全浸入水中，通过位移法来测定物质的体积。

通过测量物质的质量和体积，可以计算出物质的密度。

在实际应用中，常常会将实验测得的密度值与标准密度值进行比较，从而评估物质的纯度和稳定性。

此外，密度分析还可以用于确定物质的组成和相对密度，对于材料的鉴定、成分分析和技术评估都具有重要的意义。

密度分析还可以通过一些特殊方法和工具来实现。

例如，在测量气体的密度时，可以使用比重瓶或气体比重计来实现；在测量液体的密度时，可以使用密度计或比重计来实现。

此外，还可以利用流变仪来测量物质的流动性和变形特性，从而推断物质的密度。

总之，密度分析是通过测量物质的质量和体积，从而计算物质的密度，并据此对物质的组成、纯度和特性进行分析的方法。

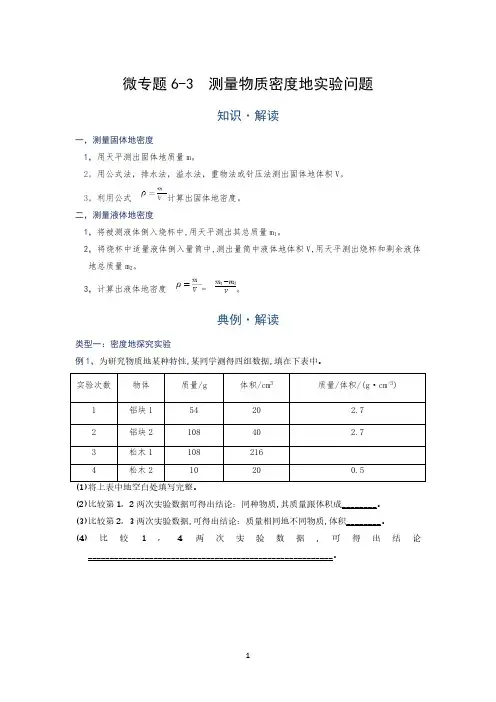
微专题6-3 测量物质密度地实验问题知识·解读一，测量固体地密度1，用天平测出固体地质量m。

2，用公式法，排水法，溢水法，重物法或针压法测出固体地体积V。

3，利用公式计算出固体地密度。

二，测量液体地密度1，将被测液体倒入烧杯中,用天平测出其总质量m1。

2，将烧杯中适量液体倒入量筒中,测出量筒中液体地体积V,用天平测出烧杯和剩余液体地总质量m2。

3，计算出液体地密度=。

典例·解读类型一：密度地探究实验例1，为研究物质地某种特性,某同学测得四组数据,填在下表中。

实验次数物体质量/g体积/cm3质量/体积/(g·cm-3) 1铝块15420 2.72铝块210840 2.73松木11082164松木210200.5(1)将上表中地空白处填写完整。

(2)比较第1，2两次实验数据可得出结论：同种物质,其质量跟体积成________。

(3)比较第2，3两次实验数据,可得出结论：质量相同地不同物质,体积________。

(4)比较1，4两次实验数据,可得出结论________________________________________________________。

类型二：液体密度地测量例2，用天平和量筒测量盐水密度地实验：(1)在使用托盘天平前要对天平进行调节,请将下面各步骤前地字母按照正确地顺序排列________。

A.组装好天平,把天平放在水平台面上B.调节天平地平衡螺母,使天平横梁水平平衡C.把游码置于标尺地零刻度线处(2)实验过程：a.在玻璃杯中盛装适量盐水,放在调节好地天平左盘上称量,当天平重新平衡时,读出砝码，游码地读数之和为m 1。

b.把玻璃杯中地一部分盐水倒入量筒,如图所示,记下量筒中盐水地体积V 。

c.把玻璃杯和剩余盐水放在天平左盘上称量,当天平重新平衡时,所用砝码和游码位置如图所示,读出玻璃杯和剩余盐水地质量m 2。

d.计算出量筒中盐水地质量m 和密度ρ(由实验过程,完成下表实验数据地填写)。

课堂笔记一、密度公式：ρ=m/V 变形公式：m=ρV 、V=m/ρ 二、密度公式的应用1、鉴别物质：利用公式ρ=m/V 求出物质的密度，再对照密度可以鉴别物质。

还可用于鉴定物质是否纯净等。

2、由公式m=ρV 可知，通过测量体积可求得不便直接测量的物体质量。

3、由公式V=m/ρ可知，通过测量质量可求得不便直接测量的物体体积。

4、判断物体是否空心，具体方法有三种：先假定物体是实心的，通过计算。

(1)如果m 实＜m 物(2)如果V 实＜V 物 则物体是空心的。

(3)如果ρ实＜ρ物【例】质量为8．8克，体积为0．55厘米3，通过计算鉴别一下这个戒指是纯金的吗?(已知金的密度为19．3×103千克／米3)【分析】 鉴别物质的方法：利用公式ρ=m/V 求出物质的密度，再对照密度表比较。

【解】根据密度公式ρ=m/V =8.8克／0.55厘米3=16克／厘米3=16×103千克／米3<19．3×103千克／米3答：该戒指不是纯金。

变式训练 一个质量为540克的铝球，体积为300厘米3，问这个铝球的是否空心?( ρ铝=2.7×103千克／米3) 作业训练1、一只最多能装下500克水的瓶子，也能装下500克的（ ） A ．柴油 B ．酒精 C ．汽油D ．浓硫酸2、三个完全相同的杯子里装有同样多的水，把质量相同的铝块、铜块、铁块(ρ铜>ρ铁>ρ铝)，分别放在三个杯子里，水面升高最多的是(水未满出) ( )A ．放铝块杯子B ．放铜块杯子C ．放铁块杯子D ．无法比较3、某钢瓶中装有氧气，瓶内气体密度为8千克／米3，在一次急救中用去了其中的3/4，则剩余气体的密度为 ( )A ．2千克／米3B ．4千克／米3C ．6千克／米3D ．8千克／米34、甲、乙两个物体是均匀的实心正方体，它们的边长之比为1：2，质量之比是1：2，则它们密度之比是 ( )A ．1：2B ．2：1C ．1：4 D_4：15、一个只能装500克水的玻璃瓶，装满水后质量为750克，改装密度为0．8×103千克／米3的酒精，则装满酒精后总质量为 ( )A ．650克B ．750克C ．850克D ．875克6、用相同质量的铝和铜制成体积相等的球，已知ρ铝=2.7×103千克／米3，ρ铜=8.9×103千克／米3则下述说法正确的是 ( )A 、球不可能是实心的B 、铝球是实心的，铜球可能是实心的C ．铜球是实心的，铝球一定是空心的D ．铝球和铜球都是实心的7．飞机设计师为减轻飞机重力，将一钢制零件改为铝制零件，使其质量减少104千克，则所需铝的质量是(ρ铁=7.9×103千克／米3，ρ铝=2.7×103千克／米3) ( )A ．35.5千克B ．54千克C ．1.04千克D ．158千克8．两块实心的正方体铁块，大的正方体边长是小的正方体边长的2倍，则大小正方体铁块的密度之比是 ，体积之比是 ，质量之比是 。

密度计算公式物理密度是物理学中一个重要的概念，它用来描述物体的质量与体积之间的关系。

密度计算公式可以帮助我们准确地计算物体的密度。

本文将介绍密度的概念、计算公式以及密度在实际生活中的应用。

一、密度的概念密度是指物体单位体积内所含有的质量，用符号ρ表示。

通常情况下，密度的单位为千克每立方米（kg/m³）。

密度是物质的一种固有特性，不随物体的大小和形状而改变。

二、密度的计算公式密度的计算公式为：密度=质量/体积，即ρ=m/V。

其中，ρ表示密度，m表示物体的质量，V表示物体的体积。

三、密度的应用密度在日常生活中有着广泛的应用。

以下是一些常见的应用场景：1. 物体的浮沉根据密度的原理，密度大于水的物体会下沉，密度小于水的物体则会浮起来。

这就是为什么金属会沉入水中而木头会浮在水面上的原因。

2. 材料的鉴别由于不同材料的密度各不相同，在鉴别材料时可以通过测量其密度来判断材料的种类。

例如，金属和塑料的密度差异较大，可以通过密度计算公式来进行区分。

3. 液体的浓度在化学实验中，密度可以用来确定溶液中溶质的浓度。

通过测量溶液的密度，可以利用密度计算公式来计算出溶质的质量浓度。

4. 建筑材料的选择在建筑领域，密度是评估材料质量的重要指标之一。

对于某些工程来说，需要选择密度较大的材料，以增加结构的稳定性和承重能力。

5. 燃料的选择燃料的密度直接影响其储存和运输的方便性。

对于相同质量的燃料来说，密度越大，所占用的空间就越小，这对于航空和航天等领域尤为重要。

密度是物体质量和体积之间的比值，可以通过密度计算公式来计算。

密度在日常生活中有着广泛的应用，包括物体的浮沉、材料的鉴别、液体浓度的确定、建筑材料的选择以及燃料的选择等。

通过了解密度的概念和计算公式，我们可以更好地理解和应用密度这一物理概念。

物质的密度与比重的计算方法密度和比重是物质特性的重要参数，它们在物理学、化学以及其他科学领域中广泛应用。

本文将介绍物质的密度和比重的计算方法。

一、密度的计算方法密度是指物质单位体积所包含的质量，用公式表示为：密度 = 质量/ 体积。

常用的密度单位为克/立方厘米（g/cm³）或千克/立方米（kg/m³）。

1. 实验法计算密度实验法是一种直接测量物质质量和体积的方法，常用于固体和液体的密度测量。

下面分别介绍固体和液体的实验法计算密度。

(1) 固体的实验法计算密度：首先称取一定质量的固体，记录其质量（单位为克，记作m1）。

然后用天平测量固体的体积，可以使用直尺测量固体的边长（单位为厘米，记作a）或者是使用密度瓶测量固体的体积。

最后计算密度的公式为：密度 = m1 / V，其中V为固体的体积。

(2) 液体的实验法计算密度：通过实验室常用的密度瓶，测量液体的质量和体积。

首先称取一个干净的密度瓶的质量（单位为克，记作m1），然后向密度瓶中加入一定体积的液体，再称重（单位为克，记作m2）得到含液体的密度瓶质量。

计算液体的质量为：质量 = m2 - m1，最后计算密度的公式为：密度 = 质量 / V，其中V为液体的体积。

2. 计算法计算密度对于某些无法直接测量质量和体积的物质，可以通过计算法来估算其密度。

下面介绍几个常用的计算法计算密度的例子。

(1) 晶体的计算法：对于晶体物质，可以通过计算晶胞中原子的质量和数量来估算其密度。

首先确定晶胞中原子的质量总和（质量记作m）以及晶胞的体积（体积记作V）。

最后计算密度的公式为：密度 = m / V。

(2) 混合物的计算法：对于多组分混合物，可以通过计算各组分质量所占的比例以及各组分的密度来估算整体混合物的密度。

首先计算各组分质量所占的比例（记作Wi，i为组分编号），然后将各组分密度乘以相应的比例后相加。

最后计算密度的公式为：密度= Σ(Wi * ρi)，其中Σ表示求和，ρi 表示各组分的密度。

密度公式ρ=m V的应用 （一）鉴别物质例1. 一只戒指看上去像是金的，怎样才能知道它是不是纯金的呢？解析：由于各种物质的密度都是一定的，不同的物质密度一般不同，所以，只要用天平测出戒指的质量，用量筒和水测出戒指的体积，由密度公式ρ=m V 求出戒指的密度，与纯金的密度比较，便能断定它是不是纯金的（也可用变形公式m V =ρ金求出纯金戒指的质量与测出的质量比较，或用变形公式V m=ρ金求出纯金戒指的体积与测出的体积比较）。

（二）求物体的质量例2. 矗立在天安门广场的人民英雄纪念碑，它的碑心是一整块巨大的花岗石，碑身高37.94 m ，厚1 m 的碑心石上刻着“人民英雄永垂不朽”，怎样知道它的质量？解析：像这类质量比较大的物体，一般无法直接用测量工具测出质量，不过由于体积规则易测，根据它的密度，用变形公式m V =ρ便可求出质量。

纪念碑体积规则易测，查出它的密度，便可求出其质量。

（三）求长度例3. 给你一架天平、一把刻度尺，如何利用它们方便、快捷地求出一卷细金属丝的长度？解析：一卷金属丝，长度较长而且卷在一起，若直接用刻度尺测，则不易。

用天平测出它的总质量M ，从中截取一小段，用天平测出这一小段的质量m ，用刻度尺测出它的长度L 0。

由密度公式得：ρ==m L S M LS0（S 为金属丝横截面积），则金属丝的总长为L M m L =0。

（四）求数量例4. 为了做好今年防汛排涝物资准备，市燃料公司采购了1500 t 柴油。

运输柴油用的油罐车容积为383m ，运完这批柴油要安排多少车次？（ρ柴油=⨯081033./kg m ） 解析：由变形公式V m=ρ求出1500t 柴油的总体积V ，除以每节油罐车容积，便可求出所安排的车次，即n V V M V ===⨯⨯⨯=≈003315001008103849350ρ..（辆）。

（五）求厚度例5. 给你一架天平、一把刻度尺，怎样求出一块长方形均匀铝薄的厚度？解析：用天平测出铝薄的质量，用刻度尺测出它的长和宽并求出面积S ，从密度表中查出铝的密度ρ，由变形公式可得V m=ρ，再由体积公式可得厚度d V S m S==ρ。

密度的物理概念密度是物体的质量和体积之比。

它是衡量物体紧密程度的物理量，通常用符号ρ表示。

密度是一个重要的物理概念，在物理学、化学、材料科学等领域里都有广泛的应用。

在常见的物质中，密度是各种物质特性之一，也是描述物质性质和变化的重要指标之一。

密度可以通过实验测量或者理论计算得到。

下面我将详细介绍密度的定义、测量方法、影响因素以及应用。

首先，密度的定义是：物体的质量除以物体的体积，即ρ= m/V，其中，ρ表示密度，m 表示物体的质量，V 表示物体的体积。

单位常用千克每立方米（kg/m ³）。

关于密度的测量，有多种实验方法。

最常见的是利用天平和体积计测量物体的质量和体积，然后计算得到密度。

在实验室中，可以使用容积瓶、皮克定理和水银密度计等设备来测量物体的体积。

而质量的测量则可以使用天平进行。

在一些特殊情况下，也可以使用其他方法来间接测量密度，例如通过声速、弹性模量、热膨胀系数等来推导物质的密度。

密度的测量结果可以得到物质的重要信息。

通过密度的测量，我们可以鉴别物质的纯度和成分。

不同物质的密度是不同的，所以密度可以作为物质鉴别的一个重要手段。

例如，黄金的密度是较高的，远高于大部分金属，所以可以通过测量密度来判别黄金的真伪。

同时，密度还可以作为物质的重要物理性质，在材料科学和技术领域中有着广泛的应用。

例如，在钢铁冶金工业中，通过调整合金材料的密度，可以改变材料的硬度、强度、韧性等机械性能。

密度的大小受多种因素的影响。

首先，物质的化学组成是决定密度的重要因素。

不同的元素和化合物具有不同的原子和分子构成，因此密度也会不同。

其次，温度和压力也会影响密度。

在常温常压下，物质的密度通常是稳定的。

然而，当温度和压力发生变化时，密度也会相应变化。

例如在相同温度下，气体的密度随着压力的增加而增加，而固体和液体的密度对压力变化不敏感。

最后，物体的状态（固体、液体、气体）也会影响密度。

通常情况下，固体的密度较高，液体的密度次之，而气体的密度最低。