北京版-数学-五年级下册-《体积单位的换算》知识讲解 体积容积单位之间的换算
- 格式：doc
- 大小：32.50 KB
- 文档页数：1
下载文档原格式
合集下载
北师大版五年级下册数学课件4.6 体积单位的换算 (共16张PPT)
3.购买那种包装的牛奶比较合算？（选自教材P45 T4）
200 mL=0.2 L
380 mL=0.38 L
2.50÷0.2=12.50(元) 3.80÷0.38=10.00(元)
9.00÷1=9.00(元)
9.00＜10.00＜12.50
答：购买第三种包装的牛奶比较合算。
4.请结合生活中的实际情况想一想，电视机包装箱的 长是60m，60dm还是60cm？宽和高呢？箱子的体积 是多少？（选自教材P45 T5）
4×3×5＝60（cm3） 6×7×9＝378（cm3） 4×4×3＝48（cm3）
2.（选自教材P45 T3）
5m3＝ ( 5000 ) dm3 720cm3＝ ( 0.72 ) dm3 3600mL＝ ( 3.6 ) L 0.5dm3＝ ( 500 ) mL
2800dm3＝ ( 2.8 ) m3 1.2m3＝ ( 1200000 ) cm3 3L＝ ( 3000 ) mL 600mL＝ ( 0.6 ) L
谢谢观赏
You made my day!
我们，还在路上……
第6课时 体积单位的换算
1. 掌握体积、容积单位之间的进率，会进行体 积、容积单位之间的换算。（重点）
2. 理解相邻体积单位之间的进率是1000的推导 过程。（难点）
常用的体积单位有 cm³、dm³、m³ 常用的容积单位有 mL、L
知识点 体积、容积单位间的进率
（1）这些棱长为1dm的正方体盒子中，可以放多少个体 积为1cm3的小正方体？想一想，填一填。
相邻两个单位间的进率 10 100 1000
知识提炼 相邻体积、容积单位之间的进率是1000。
小试牛刀
棱长为2m的正方体盒子，可以放多少个棱长为2dm 的小正方体？（选自教材P45 T1）
五年级下册数学教案-体积单位的换算 北师大版
五年级下册数学教案-体积单位的换算一、教学目标1.理解容量的概念，掌握容量单位的换算（升与毫升的互换、升与立方厘米的互换，以及毫升与立方厘米的互换）；2.能够通过实际活动和情境思维，解决容量的换算问题；3.培养学生热爱生活、乐于思考、勇于探索的学习态度。
二、教学重点1.容量单位的换算（升与毫升的互换、升与立方厘米的互换）；2.实际问题中的容量单位的换算。
三、教学难点1.毫升与立方厘米的互换；2.实际问题中的容量单位的换算。
四、教学准备1.《北师大版数学五年级下册》教材及相关教学辅助材料；2.每组学生一套大、中、小杯子；3.量杯和计时器。
五、教学内容与步骤1. 学生活动•（1）引导学生回忆上一节“长、宽、高”的换算知识；•（2）通过引导学生和老师的互动讨论、演示等形式，引入本节课的重点内容——容量单位的换算。
先从“容量”的概念入手，再引导学生认识容量单位，最后让学生初步理解容量单位的换算。
•（3）学生上台演示：通过给定的杯子和水杯，让学生从小杯子往大杯子倒水，观察水位的变化，学生需要记录下这一系列操作。
然后，学生用一个表格记录下每组的操作过程及结果（表格例如：）初始状态操作过程最终状态小杯-1ml先倒小杯-1ml，再倒中杯-5ml小杯-0ml，中杯-6ml小杯-1ml 先倒小杯-1ml，再倒中杯-5ml，最后倒大杯-20ml小杯-0ml，中杯-6ml，大杯-26ml这样不仅可以让学生更好地发现容量单位的规律，同时还可以培养学生的实际操作能力。
2. 老师指导•（1）讲解升与毫升的互换、升与立方厘米的互换，毫升与立方厘米的互换。
•（2）举一反三：让学生针对生活中的容量单位问题进行思考，并给出解决方案。
例如：需要煮一壶开水，但是需要的水量超过了家里的水壶容量，如何解决？需要借助哪些容器？3. 学生活动•（1）老师与学生进行互动，让学生获得更多实践经验，并加深对容量换算的理解。
让学生通过自己的体验，探索容量单位的换算规律。
五年级下册数学课件-第4单元 4.体积单位的换算 北师大版(共25张PPT)
知识总结
1.相邻体积、容积单位之间的进率为1000。 2.体积、容积单位之间的换算,由高级单位化成 低级单位乘进率,由低级单位化成高级单位除以 进率。
课堂作业
练习四第5、6题
谢谢大家
分别计算每种包装1L 的牛奶的价钱，然后
比较即可。
200mL
380mL
1L
2.50元
3.80元
9.00元
4.购买那种包装的牛奶比较合算？
1L的牛奶比较合算。
200mL
380mL
1L
2.50元
3.80元
9.00元
5.请结合生活中的实际情况想一想，电视机包装箱的长是60m， 60dm还是60cm？宽和高呢？箱子的体积是多少？
课堂练习
1.棱长为2m的正方体盒子，可以放多少个棱长为2dm的小正方体？
解答: 10×10×10=1000（个） 答:可以放1000个棱长为 2dm的小正方体。
2.下面每个图形的体积各是多少？填一填，与同伴说一说你是怎 么想的。（每个小正方体的棱长为1cm）
有多少个小正方体组合而成， 体积就是多少立方厘米。
相邻两个单位间的进率。
长度 面积 体积
单位 m，dm，cm m2，dm2，cm2 m3，dm3，cm3
相邻两个单位间的进率 10 100 1000
课堂练习
1.棱长为2m的正方体盒子，可以放多少个棱长为2dm的小正方体？
思路分析: 长可以摆10个，宽可以摆
10个，高可以摆10个，一共 可以摆10×10×10个。
思路分析:
正方体钢锭锻造成长方体零件,钢锭的形状发生了 变化,但它的体积没有变化,也就是说正方体钢锭的 体积与长方体零件的体积是相同的。
7.把一个棱长10分米的正方体钢锭锻造成一个底面积是25平方分米的长方 体零件,这个长方体零件的高是多少?
北师大版五年级下册《体积单位的换算》教案及作业设计(附答案)
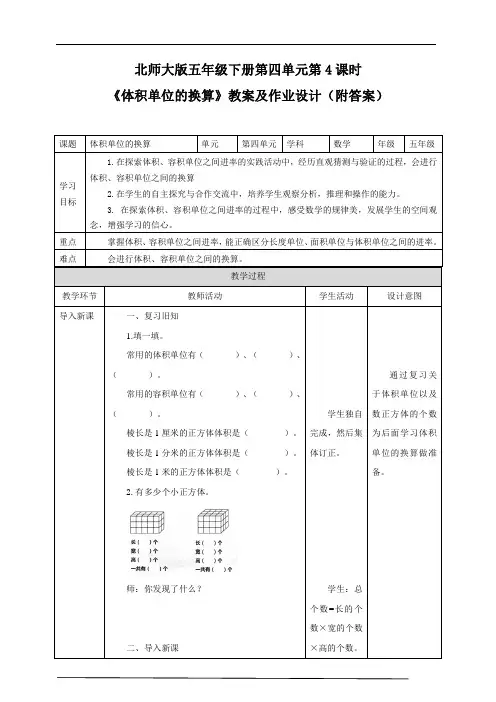
北师大版五年级下册第四单元第4课时《体积单位的换算》教案及作业设计（附答案）课题体积单位的换算单元第四单元学科数学年级五年级学习目标1.在探索体积、容积单位之间进率的实践活动中，经历直观猜测与验证的过程，会进行体积、容积单位之间的换算2.在学生的自主探究与合作交流中，培养学生观察分析，推理和操作的能力。
3. 在探索体积、容积单位之间进率的过程中，感受数学的规律美，发展学生的空间观念，增强学习的信心。
重点掌握体积、容积单位之间进率，能正确区分长度单位、面积单位与体积单位之间的进率。
难点会进行体积、容积单位之间的换算。
教学过程教学环节教师活动学生活动设计意图导入新课一、复习旧知1.填一填。
常用的体积单位有（）、（）、（）。
常用的容积单位有（）、（）、（）。
棱长是1厘米的正方体体积是（）。
棱长是1分米的正方体体积是（）。
棱长是1米的正方体体积是（）。
2.有多少个小正方体。
师：你发现了什么？二、导入新课学生独自完成，然后集体订正。
学生：总个数=长的个数×宽的个数×高的个数。
通过复习关于体积单位以及数正方体的个数为后面学习体积单位的换算做准备。
师：关于体积单位你们还想知道什么？反馈：相邻的两个体积单位之间的进率是多少？相邻的两个容积单位之间的进率是多少？师：看来大家最想知道了的是体积与容积之间的进率，那么今天我们这节课就来探讨体积单位的换算。
板书课题：体积单位的换算学生自由说一说。
先引起学生的求知欲望，然后引入课题，让人感觉顺理成章，符合学生的心理需求。
讲授新课 1.探究立方分米与立方厘米之间的关系师：你知道1dm3=( ）cm3吗？猜一猜。
反馈：1dm3=1000cm3。
师：这个答案是正确的吗？想想可以用什么办法验证一下呢？课件出示：学习任务1.想：棱长为1dm的正方体盒子中，可以放多少个体积为1cm3的小正方体呢？2.做：以小组为单位，利用手中的学具摆一摆。
3.说：你的结论是：1立方分米 =（）立方厘米师：得出结论了吗？学生自由猜一猜学生自由说一说。
数学五年级下北师大版4-4体积单位的换算课件30张
想一 想
85毫升是多少升？
想：85除以进率1000得0.085
85毫升=（ 0.085 ）升
想一 想
5.36升是多少毫升？
想：5.36乘以进率1000得5360
5.36升=（5360 ）毫升
填一 填
下面是长度单位、面积单位、体 积单位表，分别填出它们相邻两个 单位之间的进率。
单位名称
相邻两个单位间 的进率
想：①先算出长方体的体积 ②再算出一根方木的体积。 ③最后把立方米化成立方分米。
本课小结
认识体积、容积单位之 间的进率，会进行体积、容 积单位之间的换算。
绿色圃中小学教育网
平方米
4.5平方分米=（ 450 ）
平方厘米
把高级单位的数化成低 级单位的数要乘以进率；
把低级单位的数化成高 级单位的数要除以进率。
（4）什么是物体的体 积？常用体积单位有 哪些？
（5）1立方米有多大？ 1立方分米有多大？ 1立方厘米有多大？
新知 探究
棱长1分米 （10厘米）
V=1 ×1×1 V=10×10×10
解决 问题
（3）立新农具厂要砌一 道长15米、厚24厘米、高 3米的砖墙。如果每立方米 用砖525块，一共要用砖 多少块？
（1）钢板的体积： 2厘米=0.02米 2.5×1.2×0.02=0.06（立方米）
（2）钢板的重量： 0.06立方米=60立方分米 7.8×60=468（千克）
课堂作业
（1）填空。
0.01米=0.1分米
22 ×15 ×0.1=33（立方分米）
答：这块钢板的体积是33立方分米。
解决 问题
（2）把60根方木堆成一 个长3米，宽2米，高1.5 米的长方体木台，平均每 根方木的体积是多少立方 分米？
北师大版五年级下册数学《体积单位的换算》教案
北师大版五年级下册数学《体积单位的换算》教案教学目标：
1.理解体积单位的概念，如升、毫升、立方厘米等；
2.掌握体积单位的换算方法，能够完成常见单位之间的换算；
3.运用所学知识解决实际问题。
教学重点：
1.体积单位的概念；
2.常用体积单位的换算方法。
教学难点：
1.不同单位之间的换算；
2.实际问题中如何运用体积单位和换算知识解决问题。
一、引入
1.引入体积单位的概念：小明家里刚买了一桶 20 升的水，大家知道什么是升吗？它有什么作用呢？
2.通过引入实际例子，引导学生了解体积单位的概念以及其重要性。
二、讲解体积单位的概念
1.什么是体积单位；
2.常见的体积单位有哪些；
3.不同体积单位之间如何进行换算。
三、练习
1.完成以下换算练习：
（1）2 升 = ____ 毫升
（2）500 毫升 = ____ 升
（3）20 立方厘米 = ____ 毫升
（4）5 升 = ____ 毫升
（5）3 立方米 = ____ 升
2.提供实际问题，让学生尝试运用所学知识解决问题。
例：“小明妈妈买了一箱牛奶，每盒牛奶的体积为 500 毫升，一箱有 24 盒，那么这一箱牛奶一共是多少升？”
四、总结反思
1.总结体积单位的概念和常见单位的换算方法；
2.回顾练习中出现的问题以及解决方法；
3.激发学生思考，如何将所学知识运用到实际生活中。
五、作业布置
完成课堂练习和书本上相关练习。
同时，让学生整理并记录好体积单位的换算方法，以备课后复习。
五年级数学下册教案《体积单位的换算》北师大版
同学们，今天我们将要学习的是《体积单位的换算》这一章节。在开始之前，我想先问大家一个问题：“你们在日常生活中是否遇到过需要换算体积单位的情况？”（例如：换算水杯和升的关系）这个问题与我们将要学习的内容密切相关。通过这个问题，我希望能够引起大家的兴趣和好奇心，让我们一同探索体积单位换算的奥秘。
（二）新课讲授（用时10分钟）
b.难点2：在解决实际问题时，如计算一个长方体的体积，学生可能不清楚何时需要进行单位换算。教师应指导学生根据问题要求，判断是否需要换算，以及换算到哪个单位。
c.难点3：在进行体积单位换算时，学生可能因为计算步骤不熟悉而出现错误。教师需详细讲解换算步骤，并提供大量练ቤተ መጻሕፍቲ ባይዱ，让学生熟练掌握。
四、教学流程
（一）导入新课（用时5分钟）
（三）实践活动（用时10分钟）
1.分组讨论：学生们将分成若干小组，每组讨论一个与体积单位换算相关的实际问题。
2.实验操作：为了加深理解，我们将进行一个简单的实验操作。如使用容器和水来演示不同体积单位之间的换算关系。
3.成果展示：每个小组将向全班展示他们的讨论成果和实验操作的结果。
（四）学生小组讨论（用时10分钟）
1.理论介绍：首先，我们要了解体积单位的基本概念。体积单位是用来表示物体占据空间大小的单位，如立方米、立方分米、立方厘米。它们在量化物体体积、解决实际问题等方面具有重要意义。
2.案例分析：接下来，我们来看一个具体的案例。例如，计算一个长方体水箱的容量，展示如何运用体积单位换算来解决实际问题。
3.重点难点解析：在讲授过程中，我会特别强调立方米、立方分米、立方厘米之间的换算关系。对于难点部分，我会通过举例和比较来帮助大家理解。
1.讨论主题：学生将围绕“体积单位换算在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法，并与其他小组成员进行交流。
（二）新课讲授（用时10分钟）
b.难点2：在解决实际问题时，如计算一个长方体的体积，学生可能不清楚何时需要进行单位换算。教师应指导学生根据问题要求，判断是否需要换算，以及换算到哪个单位。
c.难点3：在进行体积单位换算时，学生可能因为计算步骤不熟悉而出现错误。教师需详细讲解换算步骤，并提供大量练ቤተ መጻሕፍቲ ባይዱ，让学生熟练掌握。
四、教学流程
（一）导入新课（用时5分钟）
（三）实践活动（用时10分钟）
1.分组讨论：学生们将分成若干小组，每组讨论一个与体积单位换算相关的实际问题。
2.实验操作：为了加深理解，我们将进行一个简单的实验操作。如使用容器和水来演示不同体积单位之间的换算关系。
3.成果展示：每个小组将向全班展示他们的讨论成果和实验操作的结果。
（四）学生小组讨论（用时10分钟）
1.理论介绍：首先，我们要了解体积单位的基本概念。体积单位是用来表示物体占据空间大小的单位，如立方米、立方分米、立方厘米。它们在量化物体体积、解决实际问题等方面具有重要意义。
2.案例分析：接下来，我们来看一个具体的案例。例如，计算一个长方体水箱的容量，展示如何运用体积单位换算来解决实际问题。
3.重点难点解析：在讲授过程中，我会特别强调立方米、立方分米、立方厘米之间的换算关系。对于难点部分，我会通过举例和比较来帮助大家理解。
1.讨论主题：学生将围绕“体积单位换算在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法，并与其他小组成员进行交流。
五年级下册数学教案-《体积单位的换算》北师大版
此外，学生小组讨论环节，大家的表现让我很欣慰。但在分享成果时，有些学生表达不够清晰，可能是因为他们对换算过程还不够熟悉。在今后的教学中，我会着重培养学生的表达能力和逻辑思维，让他们能够更准确地传达自己的观点。
最后，总结回顾环节，学生们对于本节课的知识点有了较为全面的掌握。但我也意识到，有些学生对换算规律的熟练程度仍有待提高。因此，我计划在课后布置一些具有挑战性的练习题，帮助学生们巩固所学知识。
（二）新课讲授（用时10分钟）
1.理论介绍：首先，我们要了解体积单位换算的基本概念。体积单位换算是用来衡量不同体积单位之间关系的数学方法。它是理解和计算物体大小的重要工具，广泛应用于我们的生活中。
2.案例分析：接下来，我们来看一个具体的案例。假设我们有一个1立方米的容器，我们要计算它能装多少个1立方分米的小球。通过这个案例，我们可以了解体积单位换算在实际中的应用，以及它如何帮助我们解决问题。
3.重点难点解析：在讲授过程中，我会特别强调1立方米=1000立方分米、1立方分米=1000立方厘米这两个重点。对于难点部分，我会通过实际物品的举例和换算练习来帮助大家理解。
（三）实践活动（用时10分钟）
1.分组讨论：学生们将分成若干小组，每组讨论一个与体积单位换算相关的实际问题，如不同容器装水的能力比较。
四、教学流程
（一）导入新课（用时5分钟）
同学们，今天我们将要学习的是《体积单位的换算》这一章节。在开始之前，我想先问大家一个问题：“你们在日常生活中是否遇到过需要换算体积单位的情况？”比如，我们在搬运东西时，可能会想知道一个立方米的箱子能装多少个立方分米的小盒子。这个问题与我们将要学习的内容密切相关。通过这个问题，我希望能够引起大家的兴趣和好奇心，让我们一同探索体积单位换算的奥秘。
最后，总结回顾环节，学生们对于本节课的知识点有了较为全面的掌握。但我也意识到，有些学生对换算规律的熟练程度仍有待提高。因此，我计划在课后布置一些具有挑战性的练习题，帮助学生们巩固所学知识。
（二）新课讲授（用时10分钟）
1.理论介绍：首先，我们要了解体积单位换算的基本概念。体积单位换算是用来衡量不同体积单位之间关系的数学方法。它是理解和计算物体大小的重要工具，广泛应用于我们的生活中。
2.案例分析：接下来，我们来看一个具体的案例。假设我们有一个1立方米的容器，我们要计算它能装多少个1立方分米的小球。通过这个案例，我们可以了解体积单位换算在实际中的应用，以及它如何帮助我们解决问题。
3.重点难点解析：在讲授过程中，我会特别强调1立方米=1000立方分米、1立方分米=1000立方厘米这两个重点。对于难点部分，我会通过实际物品的举例和换算练习来帮助大家理解。
（三）实践活动（用时10分钟）
1.分组讨论：学生们将分成若干小组，每组讨论一个与体积单位换算相关的实际问题，如不同容器装水的能力比较。
四、教学流程
（一）导入新课（用时5分钟）
同学们，今天我们将要学习的是《体积单位的换算》这一章节。在开始之前，我想先问大家一个问题：“你们在日常生活中是否遇到过需要换算体积单位的情况？”比如，我们在搬运东西时，可能会想知道一个立方米的箱子能装多少个立方分米的小盒子。这个问题与我们将要学习的内容密切相关。通过这个问题，我希望能够引起大家的兴趣和好奇心，让我们一同探索体积单位换算的奥秘。
五年级下册数学教案-4.4体积单位的换算｜北师大版
五年级下册数学教案4.4 体积单位的换算｜北师大版教案：五年级下册数学教案4.4 体积单位的换算｜北师大版一、教学内容今天我将带领大家学习北师大版五年级下册的数学知识，主要内容是体积单位的换算。
我们将通过实际例题来理解并掌握体积单位之间的换算关系。
二、教学目标通过本节课的学习，希望同学们能够理解体积单位之间的换算关系，并能够灵活运用这些知识解决实际问题。
三、教学难点与重点本节课的重点是让同学们掌握体积单位之间的换算关系，难点是能够将这些知识应用到实际问题中。
四、教具与学具准备为了更好地进行课堂教学，我已经准备好了PPT和一些实际物品，如不同体积的容器，以便同学们能够直观地理解体积单位之间的换算。
五、教学过程我会通过引入一些实际情景，让同学们感受到体积单位换算的重要性。
例如，我可以展示一个1升的水杯和一个1000毫升的水杯，让同学们观察并思考它们之间的换算关系。
在讲解完例题后，我会安排一些随堂练习，让同学们亲自动手进行体积单位的换算。
我会及时给予指导和反馈，帮助同学们巩固所学知识。
六、板书设计为了方便同学们记录和复习，我会设计一份简洁明了的板书，列出体积单位之间的换算关系，以及一些重要的提示和注意事项。
七、作业设计为了巩固同学们对体积单位换算的理解和应用，我设计了一道作业题目。
题目如下：一个水桶的容量是2000毫升，另一个水桶的容量是10升。
请问，两个水桶的容量相差多少毫升？答案：1000毫升八、课后反思及拓展延伸通过本节课的学习，我希望同学们能够掌握体积单位之间的换算关系，并能够灵活运用到实际问题中。
在课后，同学们可以进一步拓展学习，了解更多关于体积单位的知识，如立方厘米、立方米等。
同时，也可以尝试解决一些更复杂的体积单位换算问题，提高自己的数学能力。
教案：五年级下册数学教案4.4 体积单位的换算｜北师大版一、教学内容本节课的教学内容来自于北师大版五年级下册数学教材第4章的第4节，主要讲述了体积单位的换算。
北京版-数学-五年级下册-《体积单位》知识讲解 认识容积单位
认识容积单位
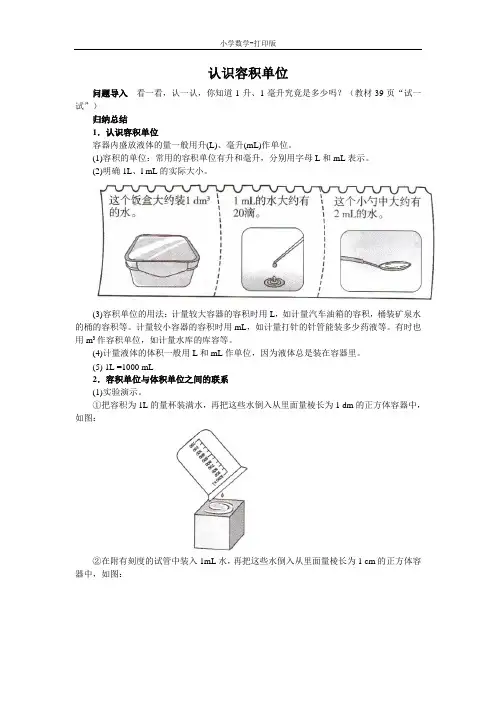
问题导入看一看，认一认，你知道1升、1毫升究竟是多少吗？（教材39页“试一试”）
归纳总结
1．认识容积单位
容器内盛放液体的量一般用升(L)、毫升(mL)作单位。
(1)容积的单位：常用的容积单位有升和毫升，分别用字母L和mL表示。
(2)明确1L、l mL的实际大小。
(3)容积单位的用法：计量较大容器的容积时用L，如计量汽车油箱的容积，桶装矿泉水的桶的容积等。
计量较小容器的容积时用mL，如计量打针的针管能装多少药液等。
有时也用m3作容积单位，如计量水库的库容等。
(4)计量液体的体积一般用L和mL作单位，因为液体总是装在容器里。
(5) 1L =1000 mL
2．容积单位与体积单位之间的联系
(1)实验演示。
①把容积为1L的量杯装满水，再把这些水倒入从里面量棱长为1 dm的正方体容器中，如图：
②在附有刻度的试管中装入1mL水，再把这些水倒入从里面量棱长为1 cm的正方体容器中，如图：
(2)实验结果。
实验①的量杯中lL的水正好注满从里面量棱长为1 dm，容积为1 dm3的正方体容器；实验②的试管中1 mL的水正好注满从里面量棱长为1 cm，容积为1 cm3的正方体容器。
(3)实验结论。
1L=1 dm3l mL=l cm3
归纳总结
1.常用的容积单位：毫升和升，分别用字母mL和L表示。
2.1升=1分米3l毫升=1厘米3 l L=l dm3 1 mL=l cm3
3.1 L=l000 mL。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
小学数学-打印版
体积溶积单位之间的换算
问题导入 3 L=( )mL 5000 dm3=( )m3
方法讲解
1．高级单位化成低级单位
(1)方法分析：1 L=l000mL，3L里有3个1L，就有3个1000 mL，即3×l000=3000(mL)。
(2)正确解答：3 L = (3000)mL。
2．低级单位化成高级单位
(1)方法分析：1000 dm3=1 m3，看5000 dm3里有几个1000 dm3，有几个1000 dm3就有几个1 m3。
5000÷1000=5，5000 cm3里面有5个1000 dm3，即5000 dm3 =5 m3。
(2)正确解答：5000 dm3=(5)m3。
归纳总结
体积、客积单位之间的换算，把高级单位化成低级单位要乘进率，把低级单位化成高级单位要除以进率。
拓展提高
6. 42 L=( )L( )mL，这是一道把单名数化为复名数的题，6. 42 L中的6表示6L，填到“L”前面的括号里；小数部分0. 42 L不够IL，把升化成毫升，乘1000得420 mL，填到“mL”前面的括号里，因此6. 42 L=(6)L(420) mL。