当前位置：文档之家 › 第二章液体的表面性质-副本

第二章液体的表面性质-副本

  • 格式：ppt
  • 大小：628.01 KB
  • 文档页数：29

下载文档原格式

  / 29

合集下载

物理学第3版习题解答-第2章液体的表面性质.

物理学第3版习题解答-第2章液体的表面性质.

第2章 液体的表面性质 2-1 如图金属框架中形成一肥皂膜，金属丝AB 长为5 cm ，可以自由滑动，拉此肥皂膜平衡时，所需的平衡力F =2.5×10-3 N ，求肥皂水的表面张力系数。

解： m N L F /105.222-⨯==α 2-2 在2-1题中，若金属丝AB 向右移动了2 cm ，试计算移动AB 所做的功。

此时肥皂膜的表面能增加了多少? 解： J S E 5105-⨯=∆=∆α 2-3 一半径为5 cm 的金属圆环，从液体中刚能拉出时，测得环的悬线上需要加F =28.3×10-3 N 的向上拉力，求此液体的表面张力系数。

(被拉起的液膜可视为很短的圆柱面)。

解 m N l F /1001.91052103.28223---⨯=⨯⨯⨯⨯==πα 2-4 把一个框架竖直地放着，其上有一条可以移动的横杆以ab ，框架之间有肥皂液膜，如图所示。

今欲使横杆保持平衡，问横杆下面应挂多大重物?已知横杆质量为0.05 g ，长度L 为2.5 cm ，肥皂膜的表面张力系数为45×10-3 N ·m -1。

解： N G l G F G ab ab 31076.12-⨯=-=-=α 2-5 移液管中有1 ml 农用杀虫药液，其密度为0.995×103 kg ·m -3。

今令其从移液管中缓缓滴出，共分30滴全部滴完。

设经过测定，已知药液将要落下时，其颈部的直径为0.189 cm ，求药液的表面张力系数。

解： m N Nd Mg /10589.52-⨯==πα 2-6 在20 km 2的湖面上，下了一场50mm 的大雨，雨滴半径r =1.0mm 。

设过程是等温的，求释放出的表面能量。

水的比表面能α=73×10-3 J ·m -2。

解： J S E 81018.2⨯=∆=∆α 2-7 吹一直径为14 cm 的肥皂泡，问需作多少功?设在吹的过程中温度不变，已知肥皂水的表面张力系数为40×10-3 N ·m -1。

大学物理第二章液体表面现象

大学物理第二章液体表面现象
解：设B、A分别为上、下液体 表面内的一点，A、B两点压强 分别为pA、pB，大气压强为p0， 则 2 2 pA p0 + pB p0 R r
2 2 pA pB + R r
2 2 pA pB + R r
pA pB gh
2 2 + gh R r
P0
f
S
f
P
2.液面弯曲
1)凸液面时，如图 s 周界 上表面张力沿切线方向，合 力指向液面内， s 好象紧 压在液体上，使液体受一附 加压强 pss ，由力平衡条件， 液面下液体的压强：
f
P0
S
Ps
f
P
p p + ps
0
ps 为正
2）凹液面时，如图
s周
界上表面张力的合力指向 外部， s 如好象被拉出， 液面内部压强小于外部压 强，液面下压强：
f
P0 Ps
S
P
f
p p ps
0
总之：附加压强使弯曲液面内外压强不等，与液面 曲率中心同侧的压强恒大于另一侧，附加压强方向 恒指向曲率中心
二、球形液面附加压强
求半径为R的球形液面的Ps 。
p0
ps pi p0
pi
O R dR
设想液滴的半径在外力作用下增大dR， 在此过程中外力做功应为 dW ps dV ， 表面积增大了dS， 液滴的表面能增加 dE dS
//
j
dl
r c
df
df

R
j
o
f df 2r sin jdl sin j 2r 0 r 2r 2 由于 sin j , 则f R R

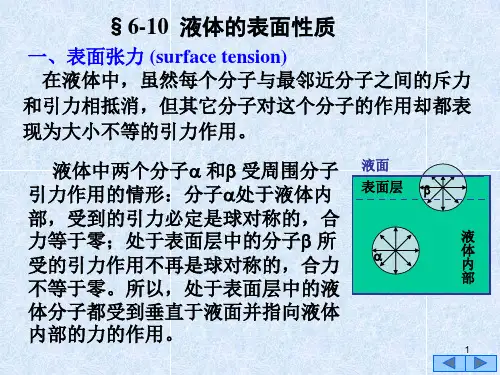
液体的表面性质-(2)

液体的表面性质-(2)
R
R
9
接触角 与毛细管内径 r
r
cos
之间的关系为
R
将上式代入
gh 2
R
得到毛细管内液面 上升的高度为
h 2 cos gr
如果液体不润湿毛细管，管内液面要比管外的 液面低 h，用同样的方法可以证明 此时 h 仍然可 由上式表示。
10
例1 如图所示的U形玻璃管，两臂的内直径分别为 1.0 mm和3.0 mm。若水与管壁完全润湿，求两臂 的水面高度差。
解 以pA表示细管内凹状水面下的 压强，以pB表示粗管内凹状水面下 的压强。压强pB应等于细管中与B同 深度的C点的压强pC，设液面上方的 气压为p0，应有p源自 = pC = pA + gh
即
p0
2
rB

p0

2
rA
gh
式中rA和rB分别为细管和粗管的内半径。 11
由上式可以解出两管水面的高度差
框架上所形成的液膜有前、后两个液面，所以 在上式中应有因子2。力 F 的功为
A =Fx =2xL = S
表面能的增加量E应等于外力所作的功A，即
E = A = S
表面张力系数 A E
S S
表面张力系数等于增加单位液体表面积时外力所 作的功，或等于增加单位液体表面积时液体表面能 的增量。
四、毛细现象 (capillarity) 当把管径很细的管子插入液体时，管子内外的液
面会出现高度差，这种现象称为毛细现象。毛细现 象是由表面张力和润湿(或不润湿)现象共同引起的。 如果液体润湿管壁，管内液面较管外高；如果液体 不润湿管壁，管内液面较管外低。
8
在右图中如液体润湿
管壁，管内液面呈现凹

02-液体的表面现象解析

02-液体的表面现象解析
1
2
M1g 1Vg N1d1 N1d1
M 2g 2 Vg N 2d 2 N 2d 2
两者相除得：
2 2Vg N 2d 2 1 1Vg N1d1
由于
1 2
2 1
d1 d 2
N1 N2
所以

得
2
N1 1 N2
水和油边界的表面张力系数 18103 N / m
其中Ps是由表面张力引起的附加压强，这表明 弯曲液面都对液体施加附加压强，其附加压强 总是指向弯曲液面的曲率中心．
１拉普拉斯公式
如图所示：一半径为Ｒ，表面张 力系数为 的球形液滴，由于是 凸液面，所以附加压强
ps pi p0
Pi和p0分别是液滴表面层内外的压强，ps为附加压强 该液面在外力作用下表面积增加ds，外力做功为
不同的液体对不同固体润湿与不润湿的程度不 同，为表明液体对固体的润湿程度，引入接触 角这个物理量． 定义：在液体与固体接触处，作液体表面和固 体表面的切线，这两条线间通过液体内部的夹 角，称为接触角
a c b d
应用：农业上制备农药时，要注意使农药润湿农作物
二
毛细现象
１毛细现象；将几根内径不同的细玻璃管插 入水中，可以看到细管中的水面会上升；相 反，如果将细玻璃管插入水银中，管内水银 面会降低，这种液体在细管中上升或下降的 现象，称为毛细现象
三
表面张力系数
１．表面张力系数两种 不同的定义： （１） 定义一；均匀液面的张力处处相等， 直线ＡＢ上任一处力的分布均相同．作用在分 界线两侧的表面张力，其大小与分界线长度Ｌ 成正比，即：
f L
或
f L
式中
＿表面张力系数，它表示作用于液体表 面单位长度线段上的表面张力．(N/m)

液体表面性质 流体力学 章节总结

液体表面性质 流体力学 章节总结

液体表面性质章节总结第二章液体表面性质1.液体表面张力液体表面张力是由于与液体交界的物质种类、形态不同产生的；表面张力大小正比于相互作用的两部液面之间假想分界直线的长度f L α=，表面张力的方向垂直于假想分界直线并与液面相切。

2.液体表面张力系数的定义α∆∆===∆∆f W E L S S表面张力系数的大小与液体的种类、温度、相邻的介质及液体的纯度有关。

3.液体表面张力形成的微观机理由于处于表面层的分子其作用球内的物质种类和密度不同，造成对该分子的引力大于斥力，表面张力是众多分子引力的宏观表现。

4.附加压强球形液面的内部压强高于球面外部的压强称为附加压强2S P Rα=任意形状弯曲液面的凹进一侧压强高于突出一测的压强1211S P R R α⎛⎫=+ ⎪⎝⎭2cos h grαθρ=毛细作用还会使细小的缝隙中悬空保持一段液体；当毛细管中混进的气体成为多个气泡时，可能会阻碍液体的流动，造成栓塞。

5.毛细现象毛细现象源于液体与固体分子之间作用力不同于表面层内液体分子之间作用力，使插入液体中的半径较小的毛细管中的液面高于或低于液槽中平液面的高度流体力学章节总结第三章流体力学1.理想流体不可压缩而且无黏滞性的流体。

定常流动流速场中各点的流速只是空间坐标的函数而不随时间变化。

2.连续性原理不可压缩、稳定流动流体单位时间内通过同一流管上任一截面的流体体积或体积流量均相同，即Sv＝恒量3.理想流体伯努利方程212v gh P ρρ++=恒量理想流体稳定流动过程中总比能守恒，即4.黏滞流体牛顿黏滞定律黏滞流体稳定流动时，流体内垂直于速度梯度的一定面积两侧流体之间的相互作用力S yv f ∆=d d η泊肃叶定律在长为L 、内径为R 的水平、等截面圆管中黏滞流体稳定流动时流速随半径的变化关系和体积流量分别为)(4)(2221r R Lp p r v −−=ηR p p R L p p Q '−=−=214218ηπ斯托克斯定律相对于黏滞流体以较低速度运动的小球所受到的阻力6f rvπη=在重力场中沉降的终极速度为229(')T r v g ρρη−=力学一般考察点一、质点力学：质点、描述质点运动物理量之间的关系、变力作功二、液体表面性质：表面张力现象、表面张力系数的影响因素、弯曲液面下附加压强、毛细管上升（下降）高度、小球在粘滞流体中运动规律三、流体力学：理想流体、连续性原理、伯努利方程、小孔流速力学重点考察点一、X，v．a微积分关系二、伯努利方程与连续性原理的应用。

物理学第3版习题解答_第2章液体的表面性质

物理学第3版习题解答_第2章液体的表面性质

4
p0 LS ( p gh
得：
4 cos )( L h) d

d ( gh 2 ghl p0 h) 4 cos ( L h)
2—23 一根直径为 1mm 的玻璃管，竖直插入盛水银的容器里，管的下端在水银面以下 1cm 处，给出 20 -3 ℃时水银的α=465×10 N/m， 问： （1） 要在管的下端吹出一半球形气泡， 管中空气的计示压强是多少？ （2） 如果管内空气压强比一大气压低 3000Pa，水银在管内会升到多高？已知水银和玻璃的接触角为 140°。 （1）解：
2-15
有两根竖直毛细管，一根直径 d1=0.50 mm，另一根直径 d2=1.0 mm，将它们插入水银中，若接
触角 =138°，求两水银柱的高度差。
h
2 cos 1 1 ( ) 10.4mm g r1 r2
2
2-16 将内直径 d=5×10-4 m 的管子浅浅地插入酒精中，流入管中的酒精质量是多少?酒精的表面张力 系数 =22.9×10-3 N·m-1，与管接触角为 0。
h2
2 1 h1 31.4mm 1 2
长 L=110 mm，内径 d=20 μm 的玻璃毛细管竖直浸入水中，毛细管的上端密封，外界空气压强
为 p0＝1.013×105 Pa，问毛细管浸入水中的长度 X 应该是多长时，才能使毛细管内的水面与外部的水面相 平? 解：根据理想气体的状态方程

F 28.3 10 3 9.01 10 2 N / m 2 l 2 5 10
2-4 把一个框架竖直地放着，其上有一条可以移动的横杆以 ab，框架之间有肥皂液膜，如图所示。 今欲使横杆保持平衡，问横杆下面应挂多大重物?已知横杆质量为 0.05 g，长度 L 为 2.5 cm，肥皂膜的表面 张力系数为 45×10-3 N·m-1。 解：

液体的表面性质

液体的表面性质

水黾行走
水黾利用液体表面的张力，在水面上行走，表面张 力使它们能够支撑在水面上。
总结和结论
1 重要性
液体的表面张力在自然界和实际应用中起着重要的作用，我们需要深入研究和利用这一 性质。
2 探索性
我们还有许多问题和挑战需要解决，例如如何调控和改变液体的表面张力。
3 未来发展
我们可以预见，液体的表面性质将在多个领域产生更多的创新和应用。
影响因素
表面张力受温度、浓度、杂 质和压力等因素的影响。不 同液体的表面张力也有所差 异。
应用领域
泡沫
表面张力使液体形成稳定的泡沫结构，广泛应用于 清洁剂、洗涤剂和食品工业。
植物水分传输
液体的表面张力使水分能够在植物体内输送，以满 足植物的生长需求。
喷墨打印
墨水喷射的精确控制需要充分利用液体的表面张力 和粘性特性。
液体的表面性质
液体的表面张力是液体分子间的相互吸引力造成的。它定义了液体表面的弹 性和紧密度，并且在许多实际应用中起着重要的角色 力引起的现象，使液体表面 的分子受到内部吸引力的牵 引，从而呈现出弹性和紧密 性。
测量方法
测量表面张力的方法包括负 压法、光滑片法和浮力测量 法等。

《液体的表面性质》课件

《液体的表面性质》课件

称不润湿。润湿与不润湿取决于液体和固体的性质以及温度等因素。
ቤተ መጻሕፍቲ ባይዱ03
吸附与解吸
在某些情况下，气体分子会吸附在液体表面上，这种现象称为吸附；当
气体分子离开液体表面时，则称为解吸。吸附和解吸在气体分离、化学
反应等领域有重要应用。
06
总结与展望
总结液体的表面性质及其应用
液体表面张力的定义
表面张力在日常生活中的应用
液体表面张力的大小与液体的微观结构有 关，如分子间的相互作用力和分子排列等 。
对未来研究的展望
探索新型表面活性剂
随着科技的发展，人们正在不断探索新型的表面活性剂，以提高液体 的表面性质，并应用于更多的领域。
表面张力与其他物理现象的关系
进一步研究液体表面张力与其他物理现象之间的关系，如毛细现象、 润湿性等，有助于更深入地理解液体的表面性质。
毛细现象
由于表面张力的作用，当细管中的液体受到外部压力时，液体会沿 着细管上升或下降，形成毛细现象。
液体表面的化学性质
01
表面活性剂的作用
表面活性剂是一种能够显著降低液体表面张力的物质。它在许多领域都
有广泛应用，如洗涤、化妆品、制药等。
02
润湿与不润湿
当液体与固体接触时，如果液体会在固体表面上展开，则称润湿；否则
02
液体表面张力的概念
表面张力定义
表面张力是指液体表面层由于分子引力不均衡而产生的沿表面作用于任一界线上的 张力。
表面张力是液体表面层由于分子引力不均衡而产生的沿表面作用于任一界线上的张 力，通俗来讲，它就是液体表面分子相互吸引形成的力。
表面张力的大小与液体的种类、温度、纯度和所接触的介质有关。
液体表面现象的普遍性

第二章+液体的表面性质

第二章+液体的表面性质

内聚力 > 附着力 液体不润湿固体 润湿 不润湿
润湿：接触角为锐角
不润湿：接触角为钝角
完全润湿：接触角为0o 完全不润湿：接触角为180o
第四节 毛细现象
液体在毛细管中上升 和下降的现象叫做毛细现象.
指尖采血 纸巾吸汗
粉笔吸水
毛细管中液面升降高度：
2 cos h gr
pB pA gh pC p0
例题2、用液滴法测农药的表面张力系数。巳知移 液管管口内半径为0.35mm，滴出的318个药滴的重 量为4.9×10-2N，求该农药的表面张力系数。
三、表面能 表面层中的分子与内部分子相比具有较高的势能。 高出的那部分势能的总和，称为液体的表面能。
力F 所作的功为 :
D A F A L B
A = F x
ΔS df 2 r o R
df 1
例题5、空气中的球形液滴或水中的球形气泡， 计算液滴和气泡内外的压强差。
2 Δp p内 p外 R
例题6、计算空气中的肥皂泡内外的压强差。
2 4 Δp p内 p外 2 R R
第三节 液面与固体接触处的性质
附着层中内聚力与附着力的抗衡 内聚力 < 附着力 液体润湿固体
A
B
气体栓塞：液体在细管中流动时 , 如果管中 有空气泡,液体的流动将受到阻碍,气泡多时可 发生阻塞,这种现象称为气体栓塞.

p1
R
r
p2
第二章 液体的表面性质
液体表面张力 弯曲液面的附加压强
毛细现象
第一节 液体的表面张力及表面能
一、表面张力的定义 液体表面存在着一种收缩力, 称之为表面张力. 表面层：几何液面以下 厚度为re的一层液体 re ：分子有效作用半径 表面层内分子密度小于液体内部 切记：表面张力 平行液面，指向液面收缩的方向

大学物理液体的表面性质

大学物理液体的表面性质

F1
2r
r R
2r 2
R
PS
F1
r 2
2
R
同理：凹液面的附加压强
PS
2
R
上两式即球形液面的附加压强公式。
二、球形液面的附加压强
球形凸液面内的液体压强：
P
P0
PS
P0
2
R
球形凹液面内的液体压强：
P
P0
PS
P0
2
R
二、球形液面的附加压强
（二）拉普拉斯公式 (Laplace formula)
如果液面不是球面，可以证明，任意弯曲液面的
三、表面张力系数 (Coefficient of surface tension )
由 f L 可得
f
L
表面张力系数的物理意义：代表液体表面张力 大小性质的物理量，数值上等于单位长度线段 两侧液面相互作用的表面张力。
σ的单位：牛顿／米（N／m）。
三、表面张力系数 (Coefficient of surface tension )
实验指出，影响表面张力系数的因素有： （1）与液体的种类相关。
（2）与相邻的介质有关。
（3）与液体的温度有关。温度愈高，液体的 表面张力系数愈小。
（4）与液体的纯度有关。液体中掺入某些物 质能显著地减小表面张力系数的大小，这种 物质称为表面活性物质。
三、表面张力系数
(Coefficient of surface tension )
240页－246页
§1 液体的表面张力
一、表面张力现象 （一）表面张力现象 （二）表面张力 二、表面张力的微观解释 三、表面张力系数 四、表面张力系数的测定
一、表面张力现象

《大学物理》第二章 液体的性质

《大学物理》第二章 液体的性质
表面张力合力 f合 的方向与液面 f
P0
Δs
Ps
f
法线方向相同，
P3
f合
S
P0
P3=P0-Ps
P3 P0 Ps
液体的性质
16
大学 物理
二、球形液面的附加压强
如图
作用在d
df
l 液d块l 上的表面张df力∥
dl
r
c
df dfsin dlsin
df// dfcos dlcos
表面张力的合力为
液体的性质
31
大学 物理
作业
• 思考题：《大学物理》2-1,2-3,2-4,2-6 • 练习题：《大学物理》2-1,2-2,2-3,2-4,2-5 • 作业题：《大学物理学习指导》第77页三、
六
液体的性质
38
P
P +ΔP
P + 2ΔP
P + 3ΔP
P + nΔP
同理，要使第二个液滴移动，第二个气泡中的压强必须必须大于 P + 2ΔP 。 如果要使这 n 个液滴移动，则最右端必须施以大于P + nΔP 的压强。
当液体在毛细管中流动时，如果管中出现气泡，液体的流 动会受阻，如果气泡产生得多了，就会堵住毛细管，使液滴不 能流动。这种现象称为气体栓塞现象。
内聚力大于附着力
内聚力小于附着力
A
f 不润湿
f A
润湿
液体对固体的润湿程度由接触角来表示。
接触角：在液、固体接触位置作固体表面与液面切线，经过液
体内部与液体表面所夹的角。通常用q 来表示。
当 q 时，液体润湿固体；
2
q
当 q 时，液体不润湿固体；

大学物理学：液体的表面层性质

大学物理学：液体的表面层性质

毛细现象
把一块洁净的玻璃浸入水银里再取出来，可以看到 玻片上不附着水银；在洁净的玻璃板上放一滴水银， 水银能够在玻璃板上滚来滚去，也不附着在上面， 这种液体和固体接触面积趋于缩小的现象称为不浸 润现象。对玻璃来说，水银是不浸润液体。
接触角为与液面相切的切线和固-液界面之间的夹角
浸润和不浸润现象
接触角为与液面相切的切线和固-液界面之间的夹角
由于表面活性物质在溶液中聚集于极薄的表面层， 所以少量的表面活性物质就可以显著降低溶液的 表面张力系数。反之，表面非活性物质溶于溶剂 后，这些物质将尽可能离开表面层，进入液体内 部，以减少表面能，结果溶液内部溶质的浓度比 表面层大。
表面吸附
表面吸附
表面吸附
表面吸附
由图可以看出，力f1 和f12有使液滴紧缩的趋势；力f2有 使液滴伸展的趋势。当
弯曲液面的附加压强
P0=P
弯曲液面的附加压强
P P0 PS P P0
P0 P PS
P P0
弯曲液面的附加压强
2
PS R
P0=P
弯曲液面的附加压强
P P0 PS P P0
P0 P PS
P P0
肥皂泡内外压强差为：PS
பைடு நூலகம்
4
R
附加压强实验
在玻璃管的两端吹两个半径不 等的肥皂泡A和B。由于小泡的半径 较小，所以泡内的压强就较大。当 打开阀门使两泡连通时，小泡内气 体将流入大泡，小泡逐渐缩小，大 泡逐渐变大，直至小泡缩减为弯曲 液层，且与大泡有相同的曲率半径
表面吸附
表面吸附
由图可以看出，力f1 和f12有使液滴紧缩的趋势；力f2有 使液滴伸展的趋势。当
2 1 12 时，则 f2 f1 f12

液体表面的性质

液体表面的性质

03 液体表面的化学性质
表面活性剂
01
表面活性剂是一种能够显著降低液体表面张力的物质，通常具 有亲水基团和疏水基团。
02
表面活性剂在液体表面形成分子膜，降低表面张力，使得液体
易于润湿和铺展。
表面活性剂在洗涤、化妆品、制药等领域广泛应用，如肥皂、
03
洗发水、沐浴露等产品中都含有表面活性剂。
表面吸附现象
表面张力
液体表面存在一种使液面尽可能缩小 的力，称为表面张力。表面张力的大 小可以用表面张力系数来衡量。
表面能
由于表面张力的存在，液体表面具有 一定的能量，称为表面能。表面能的 大小与液体的种类、温度和压力等因 素有关。
弯曲液面的内外压力差弯曲来自面内外压力差当液体表面弯曲时，液面内侧受到的 压力大于液面外侧受到的压力，形成 一定的压力差。这个压力差的大小与 液体的种类、温度和弯曲程度等因素 有关。
液体表面的性质
目录
• 液体表面的基本概念 • 液体表面的物理性质 • 液体表面的化学性质 • 液体表面的应用 • 液体表面现象的实验研究方法
01 液体表面的基本概念
液体表面的定义
总结词
液体表面是指液体与气体接触的界面。
详细描述
液体表面是液体与气体之间的分界面，它具有特定的物理和化学性质。在这个 界面上，液体的分子与气体分子相互作用，形成了一种特殊的分子排列。
滴重法
在液面上放置一块固体，测量固体因毛细作用上升的高度，结合已知的液体密度和重力 加速度，计算表面张力。
THANKS FOR WATCHING
感谢您的观看
生物医学工程
表面张力在生物医学工程中也有 应用，例如在制备生物材料和药 物传递系统方面。
弯曲液面的应用

《大学物理》第二章 液体的性质

《大学物理》第二章 液体的性质

则液体表面的张力系数： F mg
2L
液体的性质
6
大学
二、表面张力系数
物理
液体的性质
7
大学
二、表面张力系数
物理
2）液滴测定法将质量为 m 的待测液体吸 入移液管内，然后让其缓慢地流出。
当液滴即将滴下时，表面层将在颈部 发生断裂。此时颈部表面层的表面张力均 为竖直向上，且合力正好支持重力。
用附有目镜测微尺的望远镜测得断裂痕的直径为
df
df⊥R
f f df dlsin
sin dl 2rsin
o
由于sin r
R
，所以 f 2r 2 得
R
PS
f
r 2
2
R
球形弯曲液面的附加压强与表面张力系数成正比，
与液面的曲率半径成反比。
液体的性质
17
大学 物理
二、球形液面的附加压强
如凸果球液形面液外 面大 内气 液压 体为压强P0，为在P平衡P0状态2R下，
力共同作用引起的。
如果液体对固体润湿， 则接触角为锐角。
如果液体对固体不润湿， 则接触角为钝角。
固
h
B体 A
液体
固 体 液体 h
液体的性质
25
大学
二、毛细现象
物理
2、毛细管中液面上升或如图下，降一的截高面度半径为 r 的毛细圆管，
R
r
P0 Aθ
h
液体润湿管壁，接触角为q 。
设管内液面为一半径为 R 的凹球面
面层分子比液体内部分子的相互作用势能大。
由势能最小原则，在没有外力影响下，液体应处于
表面积最小的状态。
液体的性质
13
大学 物理

[理学]第二章液体表面性质

[理学]第二章液体表面性质
置附近作微小振动。
• 液体没有一定形状，并具有流动性。 液体分子振动的平衡位置不固定，是近程有序，即 在很小范围内在一短暂时间里保持一定的规则性。
液体表面：
液体与气体、固体接触时，交界处形成表面层及附着 层。
第二章 液体表面性质
2.1 液体的表面张力 一、表面张力
1.现象：
（1）蚊子能够站在水面上； （2）钢针能够放在水面上； （3）荷花上的水珠呈球形； （4）肥皂膜的收缩；
不润湿：液体在固体表 面上收缩的现象，称液 体不润湿固体。
润湿、不润湿与相互接触的液体、固体的性质有关。
第二章 液体表面性质
2. 接触角
在液体与固体接触面的边界处任取一点，作液 体表面及固体表面的切线，这两切线通过液体内部 的夹角称接触角 ，用θ 表示。
⑴力
(1)表面层：在液体与气体交界面，厚度等于分 子有效作用半径R 的一层液体。 R=10-9m
(2)表面张力：液体的表面层中有一种使液面尽可 能收缩成最小的宏观张力。
第二章 液体表面性质
(3)表面张力产生的原因 ①从分子运动论观点说明
液面 表面层
R
分子作用球：在液体中，一个
引力作用半径R 的球。
一：附加压强的产生
1.平液面
在液体表面上取一小面积△S ,
由于液面水平，表面张力沿
水平方向，△S 平衡时
P0
f
S f
P
ps p p0 0
s 第二章 液体表面性质
2.液面弯曲
1)凸液面
附加压强为：
ps p p0 0
2） 凹液面
附加压强为：
p p p 0
s
0
P0
f
S f
Ps P

第2章 液体表面

第2章 液体表面

2018/8/17
• 例：试求25℃，质量m＝1g的水形成 一个球形水滴时的表面自由能E1。 若将该水滴分散成直径2nm的微小水 滴，其总表面能E2又是多少？（已 知25℃时水的比表面自由焓Gs为 72×10-3 J*m-2)
2018/8/17
表面张力（surface tension）
在两相(特别是气-液)界面上，处 处存在着一种张力，它垂直与表面的 边界，指向液体方向并与表面相切。 把作用于单位边界线上的这种力 称为表面张力，用 表示，单位是 N· m-1。 将一含有一个活动边框的金属 线框架放在肥皂液中，然后取出悬 挂，活动边在下面。由于金属框上 的肥皂膜的表面张力作用，可滑动 的边会被向上拉，直至顶部。
2018/8/17
式（2-30）也可以改写成
a 2 / Dr g rh
2
修正方法之一是Rayleigh提出的级数近似法
a r (h r / 3 0.1288r / h 0.1312r / h
2 2 3
2
)
式中第一项是基本的Laplace方程，第二项是 考虑弯月面液体质量的修正，其余各项是 对偏离球形的修正，得 σ=1/2Δρga2
表面张力与温度的关系
温度升高，界面张力下降，当达到临界温度Tc时， 界面张力趋向于零。
Ramsay和Shields提出的 与T的经验式较常用:
Vm2/3 =k（Tc-T-6.0）
式中Vm为摩尔体积，k为普适常数，对非极性液 体，k =2.2×10-7 J· K-1 。
2018/8/17
2.3 弯曲表面下的附加压力与蒸气压
第二章 液体表面
2018/8/17
2.1 表面功（surface work）
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
值不同。
与温度有关：温度升高，α值减小，两者近似呈线性
关系。( P69 表4-1 ) 与液体内所含杂质有关：在液体内加入杂质，液体
的表面张力系数将显著改变，有的使其α值增加；有 的使其α值减小。使α值减小的物质称为表面活性物
质。
例1：常温下油以水为界的表面张力系数 为1.85Ⅹ10-2N/m，将质量为1g的油在水 内散布成半径为5μm的小油滴，需要做多 少功？(ρ=0.82Ⅹ103kg)
张力。
表面张力
• 不是由弹性形变引起的，而是分子力作 用的结果
• 分子力随分子间距的变化（引力和斥力）
3表面张力产生的原因
1. 从分子运动论观点说明
分子作用球： 在液体内部
任取一分子A ,以 A为球心，以分 子有效作用半径 R 为半径作一球， 称为分子作用球 。 球外分子对A 无 作用力，球内分 子对A 的作用力 对称分布，合力 为零。
第二章 液体的表面性质
§2.1 液体的表面张力
一、表面张力
1.现象：
(1)液面有收缩到最小的趋势；
(2)液面像紧绷的橡皮膜具有弹性。
说明：液面上存在沿表面的收缩力作用，这种力 只存在于液体表面。
2.表面张力 (1)表面层：在液体与气体交界面，厚度等于分
子有效作用半径R e的一层液体。 (2)表面张力：使液面尽可能收缩成最小的宏观
表面张力系数为α，将AB边无 摩擦、匀速、等温地右移△x，
A A f F
在AB边上加的力为：F =2αl ，
则在这个过程中外力F 所做的
B B
功为: A Fx 2lx S
其中△S = 2l△x ,是AB 向右移动过程中液面面积的增
量。外力克服表面张力做功，表面能增加，若用△E
表示表面能增量，则：
f
S f

P
2.液面弯曲
P0
1)凸液面时，如图ΔS周界上 表面张力沿切线方向，合力 指向液面内， ΔS 好象紧压 在液体上，使液体受一附加
压强 ，由力p 平衡条件，液
面下液体的压强：
f
S f
P
P
p p0 p Δp为正
附加压强与外部压强方向相同，为正；相反则 为负。
2）凹液面时，如图ΔS 周界上表面张力的合力指 向外部,ΔS如好象被拉出， 液面内部压强小于外部压 强，液面下压强：
举例
P大内
P0
P0
P
f
f
S
P
p p0 p
Δp为负
总之：附加压强使弯曲液面内外压强不等，与液面 曲率中心同侧的压强恒大于另一侧，附加压强方向 恒指向曲率中心
三、 球形液面附加压强
如图球形液面上的一小液面， 在周界上取一线元dl，作用 在dl上的表面张力
df dl
df //
j dl
r
c
df
df
Rj
df力的方向垂直dl且与球面相切。将df分
解为半径r垂直和平行的两个分力df∥与
o
/
df⊥
df//
df cosj
dl cosj
df df sinj dl sin j
由圆对称性，在圆周界上 的其他线元上，作用着同
// j dl r
c
样大小的表面张力，这些 力的水平分力相互抵消， 垂直分力方向相同，合力
df
df
Rj
为：
o
f
df
2r
0
sin
jdl
sin
j
2r
由于 sin
j
r R
, 则f
2r 2
R
f
2r 2
R
附加压强
p f 2 r2 2 r2 R r2 R
——拉普拉斯球面附加压强公式
球形液面附加压强与表面张力系数成正比，与球面半径R 成反比。半径越小，附加压强越大；半径越大，附加压强
越小；半径无限大时，附加压强等于零，这正是水平液面
自然界中有许多情况下液面是弯曲的，弯曲 液面内外存在一压强差，称为附加压强, 用△P 表 示。附加压强是由于表面张力存在而产生的。
一：附加压强的产生
1.平液面 在液体表面上取一小面
积△S ,由于液面水平，
表面张力沿水平方向，
△S 平衡时，其边界表面 张力相互抵消,△S 内外
压强相等： P P0
P0
的情况。
凸液面：p
p0
2
R
凹液面：p
p0
2
R
三.球形液膜内、外压强差
如图,由于球形液膜很薄，内外 膜半径近似相等，设A、B、C 三
点压强分别为PA 、PB 、PC ，则：
PB
PA
2
r1
PB
PC
2
r2
PA
2
r1
PC
2
r2
r1 r2 R
PC
PA
4
R
膜内压强大于膜外压强，
并与半径成反比。
CB A R •O
任何系统的势能越小越稳定，所以表面层内 的分子有尽量挤入液体内部的趋势，即液面有 收缩的趋势，这种趋势在宏观上就表现为液体 的表面张力。表面张力是宏观力，与液面相切; f ⊥是微观力，与液面垂直。
(4)表面张力系数
我们想象在液面上画一条 f
直线段，线段两侧液面均有收
缩的趋势，即有表面张力作用，
该力与液面相切,与线段垂直，
E A S
E A
S S
表面张力系数在数值上等于增加液体单位表面积时，外力所
需做的功，或增加液体单位表面积时，表面能的增加。
(6)影响表面张力系数的因素
与液体的性质有关：不同液体，α值不同；密度小、 易挥发的液体α值较小。如酒精的α值很小，金属 熔 化后的α值很大。 与相邻物质性质有关：同一液体与不同物质交界，α
解：外界做功用于增大油的表面积。
设：N为小油滴的数目，r为半径。R为大油滴半
径 则表面积增量为：△S=N4πr2-4πR2
（1）
外力做功为 A=αΔS
（2）
求R：由质量不变有
m 4 R3 N 4 r3
3
3
(3)
将（1）、（3）带入（2）得A 3m [1 ( 4 )1/3 ]
r 3m
§2.2 弯曲液面的附加压强
从表面层中任
取一分子B，其受
合力与液面垂直，
指向液内，这使得
表面层内的分子与
液体内部的分子不
f
同,都受一个指向
液体内部的力。
在这些力作用下，
液体表面的分子有
被拉进液体内部的
趋势。在宏观上就表现为液体表面有收缩的趋势。
2.从能量观点来分析
把分子从液体内部移到表面层，需克服 f ⊥ 作 功;外力作功,分子势能增加,即表面层内分子的 势能比液体内部分子的势能大，表面层为高势 能区。
指向各自的一方,分别用f 和f′表
f
示，这恰为一对作用力与反作
用力， f = - f′。
由于线段上各点均有表面张力作用,线段越长,则合 力越大。设线段长为l ,则：f =αl 。
α为表面张力系数，数值上等于单位长度直线段两
侧液面的表面张力，单位：N / m 。
(5)表面张力系数与表面能增量
如图所示，铁丝框上挂有液膜，