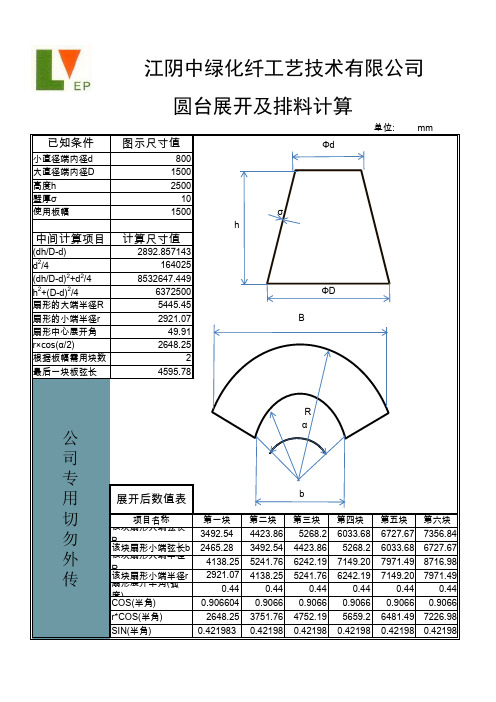
n傻瓜式圆台展开方法带公式及CAD图示(xls表格)
- 格式:xls
- 大小:65.50 KB
- 文档页数:4

圆台体积公式和表面积
圆台是指由两个同心圆面和它们之间的部分组成的几何体。
圆台有一个较小的底面、一个较大的底面和一个斜面。
它可以用以下公式计算其体积和表面积。
首先,我们来看圆台的体积公式。
假设圆台的底面半径为R,顶面半径为r,高为h。
那么它的体积公式为:
V = 1/3 * π * h * (R^2 + R*r + r^2)
其中,π是一个常数,约等于3.14159。
这个公式是通过将圆台分解为许多无穷小的圆柱体,并将它们的体积相加而得出的。
该公式的推导过程可以在数学书籍或在线数学资源中找到。
接下来,让我们看一下圆台的表面积公式。
假设圆台的底面半径为R,顶面半径为r,斜面的侧面角为α,高为h。
那么它的表面积公式为:
A = π * (R+r) * l + π * R^2 + π * r^2
其中,l是圆台的母线长度,可以使用勾股定理计算:
l = √(h^2 + (R-r)^2)
注意,圆台的表面积由三个部分组成:侧面积、底面积和顶面积。
侧面积可以通过将圆台展开成一个扇形并计算弧长来计算。
底面积和顶面积则分别为一个圆的面积。

圆台侧面的展开的两种方法
圆台是圆锥平行地切去顶部得到的剩下的一部分,它的上底面和下底面平行,圆台的立体图见Fig 1:
Fig 1 圆台实图
如果沿着圆台的母线即剪开圆台,如图Fig 2,并展开剪下来的图形,那么会得到什么样的图形呢,下面我们从两个思路出发解答这个问题。
Fig 2 圆台立体图
第一种方法:利用圆台的定义。
圆台是圆锥平行地切去顶部得到的剩下的一部分,那么是不是可以从圆锥的展开图中得到圆台的展开图呢,而圆锥的展开图是一个扇形,这是大家都知道的,圆锥的立体图和展开图如图Fig 3(a)和Fig 3(b)。
Fig 3(a) 圆锥立体图Fig 3(b) 圆锥展开图
这样我们想象把圆锥剪开和圆台剪开的区别,就是一个大圆锥减去一个相似的小圆锥就是圆台,那么对应的展开图也是一样一个大扇形减去一个小扇形,就是圆台的展开图,如图Fig 4。
Fig 4 圆台展开图
第二种方法:想象圆锥极端的情形。
如果把圆锥的锥角看成0度,那么圆台也就变成了圆柱,而圆柱我们是知道的,它的展开图是一个矩形,这个时候母线与底面曲线展开的曲线(弧度为无穷,变成了直线)是垂直的,那么换成圆台显然就不垂直了,而是和底面曲线展开的圆弧的切线垂直,那么就得到了如图Fig 4的图形。

教您用几何画板制作圆台
圆台是一种上面小下面大的立体图形,在几何画板里面究竟能够怎样最快的制作出圆台呢?下面就让我们一起来看看几何画板圆台的制作方法。
一、绘制圆台
1.打开几何画板,单击侧边栏“自定义工具”——“立体几何”——圆台。
选择“自定义工具”——“立体几何”——“圆台”示例
2.用鼠标在空白位置点一下确定圆台底面圆圆心,用鼠标拖动调整好圆台的大小和方向再单击鼠标即可绘制出圆台。
利用几何画板自定义工具绘制圆台示例
二、调整圆台
1.调整圆台大小和方向
按住底面圆的圆心红点拖动,可以调整底面圆的大小从而调整圆台大小,并通过旋转调整圆台的方向。
拖动底面圆的圆心调整圆台大小和方向
2.调整圆台的位置
按住圆台上面的任何一条线上下左右拖动都可以调整圆台水平和垂直位置。
拖动圆台上面的线调整圆台的位置
三、美化圆台
此时的圆台看上去有一些多余的线条我们选择这些线条单击右键选择“隐藏线段”,即可去掉。
此时在右侧边还少一条线,我们可以调用“线段直尺工具”画一条线即可。
隐藏不必要的对象并构造线段来美化圆台
以上教程向大家介绍了几何画板圆台的制作方法,其实利用自定义工具可以快速画出很多图,为制作课件节省了大量的时间。

怎样利用几何画板“准确”画出圆锥、圆台的展开图?一、利用几何画板“准确”画出圆锥的展开图:圆锥的展开图是一个侧面展开的扇形图和底圆构成,要较“准确”画出其全面展开图,可按下面的操作来完成.我分为两种情况简单谈谈:1.根据底圆周长来画出侧面展开图:⑴.先通过“度量”测量出圆锥的底圆的半径和圆锥的母线长;见下面左截图图中数据标签(标签名称和精确度可以在“属性”里修改).⑵.选取两个点分别作为底圆的圆心和扇形的圆心,分别同时选定点和数据标签,通过“构造”→“以圆心和半径绘圆”→ 点击即可绘出相应的圆(见下面左截图的两个圆).⑶.利用周长公式计算出底圆的周长,因为底圆的周长就是就是侧面展开图扇形的弧长,所以利用扇形的弧长公式输入底圆的周长和扇形的半径(即圆锥的母线长),再可以通过“数据”→“计算”算出扇形的圆心角的度数.可以分步计算,也可以“一气呵成”(见上面的右截图),式子中的π可以通过数据→ 计算 → 数值的下拉中点选输入,也可以取近似值,比如 3.14π≈,最后确定即可.可以将此数据标签名称改写成“扇形圆心角”).⑷.在圆锥母线长为半径构成的圆中 → 取一半径 → 标记其圆心为旋转中心 → 将半径的另一端点或半径旋转扇形圆心角的度数.(旋转时只需线先选定要旋转的点或半径 →再“变换” → “旋转” → 点选“圆心角度数”的数据标签 →“旋转”即可完成旋转) → 构造两半径所夹的弧(在弧上任取一点,然后通过“过三点的弧”解决.)(见下面左截图)⑸.将不需要的点线隐藏,设置留下的点线的大小和颜色,调整复制到Word 中供试卷编制使用,一个较“准确”的圆锥全面展开图即完成(见上面的右面两个截图).2.根据侧面展开图画底圆:本问题是已知圆锥的侧面展开图,关键是怎样确定底圆?可按下面的步骤操作:⑴.先测量出扇形的半径和圆心角(见下面左截图)⑵.计算出扇形的弧长,再圆周长公式计算出底圆的半径,可以分步进行,也可以“一气呵成”(见上面的右截图).可将此标签通过“属性”改写成“底圆半径”名称. 更醒目(见下面的左截图)⑶.任取一点为圆心,以此点和“底圆半径”构造底圆.,将扇形和底圆处理成所需要形式,最后复制到Word中供试卷编制使用(见上面的右面两个截图)二、利用几何画板“准确”画出圆台的展开图:1.圆台实际上可以看作是大圆锥平削上面的一个小圆锥而成的. 圆台的展开图实际上是由两个底圆和一个侧面(是圆环的一部分,可以叫做“扇环”),利用几何画板要“准确”画出圆台的展开图其操作和前面的相似,只不过要先延长圆台两对应的边线找交点(见下面的左面截图),才能进一步测出大小圆锥的母线长.这是个关键!圆台的侧面展开图,要在两个同心圆中来操作,要分别在大小圆中进行构造圆心角相同的弧,其操作和前面的相似(见下面的中间截图).最后隐去不需要的部分后和两个底圆处理成所需要格式(见下面的右面截图).2.若要根据圆台的侧面展开图来画圆台的两个底圆,要先把侧面的共同的圆心角找出来,还是要延长“扇环”两端的边线找出交点,也就是两扇形的圆心(见下面的截图),然后通过“度量”测量出圆心角和和两扇形的半径;然后再按前面的操作计算出两个底圆的半径,从而画出两个底圆,此操作在这里不再赘述.郑宗平2016/4/15。

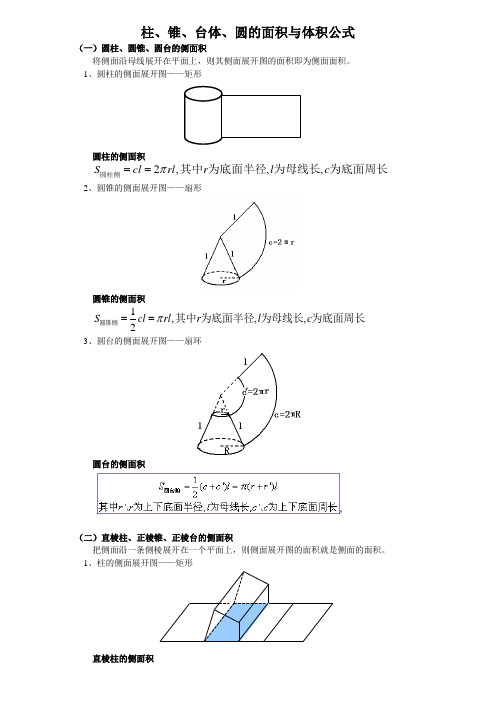
柱、锥、台体、圆的面积与体积公式(一)圆柱、圆锥、圆台的侧面积将侧面沿母线展开在平面上,则其侧面展开图的面积即为侧面面积。
1、圆柱的侧面展开图——矩形圆柱的侧面积2,,,S cl rl r l c π==圆柱侧其中为底面半径为母线长为底面周长2、圆锥的侧面展开图——扇形圆锥的侧面积1,,,2S cl rl r l c π==圆锥侧其中为底面半径为母线长为底面周长3、圆台的侧面展开图——扇环圆台的侧面积(二)直棱柱、正棱锥、正棱台的侧面积把侧面沿一条侧棱展开在一个平面上,则侧面展开图的面积就是侧面的面积。
1、柱的侧面展开图——矩形直棱柱的侧面积2、锥的侧面展开图——多个共点三角形正棱锥的侧面积3、正棱台的侧面展开图——多个等腰梯形正棱台的侧面积说明:这个公式实际上是柱体、锥体和台体的侧面积公式的统一形式 ①即锥体的侧面积公式;②c'=c 时即柱体的侧面积公式;(三)棱柱和圆柱的体积,V Sh h =柱体其中S 为柱体的底面积,为柱体的高斜棱柱的体积=直截面的面积×侧棱长(四)棱锥和圆锥的体积1,3V Sh h =锥体其中S 为锥体的底面积,为锥体的高(五)棱台和圆台的体积说明:这个公式实际上是柱、锥、台体的体积公式的统一形式:①0S=上时即为锥体的体积公式;②S上=S下时即为柱体的体积公式。
(六)球的表面积和体积公式(一)简单的组合几何体的表面积和体积——割补法的应用割——把不规则的组合几何体分割为若干个规则的几何体;补——把不规则的几何体通过添补一个或若干个几何体构造出一个规则的新几何体,如正四面体可以补成一个正方体,如图:四、考点与典型例题考点一几何体的侧面展开图例1. 有一根长为5cm,底面半径为1cm的圆柱形铁管,用一段铁丝在铁管上缠绕4圈,并使铁丝的两个端点落在圆柱的同一母线的两端A、D,则铁丝的最短长度为多少厘米?D CBA解:展开后使其成一线段ACcm考点二求几何体的面积例2. 设计一个正四棱锥形的冷水塔顶,高是0.85m,底面的边长是1.5m,制造这种塔顶需要多少平方米铁板?(保留两位有效数字)ESO解:)m (40.313.15.1214S 2=⨯⨯⨯=⇒答:略。

推导圆台的表面积公式圆台是指由一个底圆和与底圆平行的侧面组成的几何体。
在几何学中,我们可以通过推导来得到圆台的表面积公式。
下面,我将按照推导的逻辑顺序,依次介绍推导圆台表面积公式的过程。
首先,我们需要明确圆台的几何特征。
一个圆台由一个底圆和与底圆平行的侧面组成,底圆的半径为r,侧面的高度为h,侧面与底圆的夹角为α。
我们的目标是推导出圆台的表面积公式。
我们从最简单的情况开始推导。
考虑一个底圆半径为r,侧面高度为h,且侧面与底圆夹角为90度的情况。
这样的圆台可以看作是一个圆柱体,它的表面积公式为:圆台的侧面积= 2πrh圆台的底面积= πr^2圆台的表面积 = 底面积 + 侧面积= πr^2 + 2πrh接下来,我们考虑圆台侧面与底圆非垂直的情况。
我们将侧面与底面的交线固定在底面上的一个点P上,构造直角三角形OPQ(如下图所示),其中O为底面圆心,Q为圆台侧面与底面的交线与圆心O的连线与底面的交点,P为底面上的固定点。
[图]O/ |/ |/ |/ |/ |P Q|_____|在直角三角形OPQ中,OQ为圆台的半径r,OP为圆台的高度h,PQ为圆台的侧面与底面的交线段长度。
根据勾股定理,我们可以得到:OQ^2 = OP^2 + PQ^2将OQ替换为r,OP替换为h,我们可以得到:r^2 = h^2 + PQ^2化简后可得:PQ = √(r^2 - h^2)由几何性质可知,当交线固定时,所有的Q点构成底面上的圆,其半径等于圆台的半径r。
因此,PQ实际就是底面圆的周长,即2πr。
我们可以得到以下关系式:PQ = 2πr将上述关系式代入之前的公式,我们可以得到圆台的侧面积公式:圆台的侧面积= PQ×h = 2πrh综上所述,当圆台的底圆半径为r,侧面高度为h,侧面与底圆夹角为α时,圆台的表面积公式为:圆台表面积 = 底面积 + 侧面积= πr^2 + 2πrh通过以上的推导过程,我们得到了圆台的表面积公式。


斜圆台侧面积公式斜圆台是一个相对复杂但又十分有趣的几何图形。
咱先来说说斜圆台到底是个啥。
想象一下,你有一个圆台,但是它不是正正好好地立在那儿,而是有点倾斜,这就是斜圆台啦。
斜圆台的侧面积公式可不是一下子就能轻松记住的。
它就像一个小怪兽,需要咱们一步步去征服。
公式是:$S = \pi l (r + R)$,这里的$l$是母线长,$R$和$r$分别是上底面和下底面的半径。
为了让大家更好地理解这个公式,我给大家讲个我曾经碰到的事儿。
有一次我在课堂上讲斜圆台的侧面积,有个同学就一脸懵地问我:“老师,这公式咋来的呀,感觉好难记。
”我当时就笑了,说:“别着急,咱们一起来研究研究。
”我拿出了一个纸做的斜圆台模型,把它展开。
大家就看到了,原来斜圆台的侧面展开图是一个扇环。
然后我们一起计算扇环的面积,发现就是上面那个公式。
我让同学们自己动手做模型,再展开,通过实际操作去感受。
有个调皮的小家伙,做模型的时候还不小心把纸撕破了,急得直挠头。
但经过努力,大家最终都明白了公式的由来。
回到这个公式,咱们来仔细分析分析。
母线长$l$起着关键作用,它决定了侧面展开图的大小和形状。
而上下底面的半径$r$和$R$,则影响着扇环的宽窄。
在实际应用中,这个公式可有用啦。
比如说,建筑工人要给一个斜着的圆柱形水塔做外层包裹,那就得用到斜圆台侧面积公式来计算材料的用量。
再比如,设计师在设计一个独特的斜圆台形状的灯罩时,也得依靠这个公式来确定所需布料的面积。
总之,斜圆台侧面积公式虽然看起来有点复杂,但只要咱们多动手、多思考,就能轻松掌握,并用它来解决好多实际问题。
希望大家以后看到斜圆台,不再害怕,而是能自信地运用这个公式,算出它的侧面积。
加油,小伙伴们!。

初三数学圆柱 圆锥 圆台的侧面展开图及计算 浙江版一. 本周教学内容: 圆柱、圆锥、圆台的侧面展开图及计算 二. 重、难点:用侧面展开图的面积公式去计算圆柱、圆锥及圆台的侧面积、表面积等问题。
三. 知识回顾:1. 梳理圆柱、圆锥和圆台的基本结构知识。
2. 复习旋转面、轴截面、侧面展开图以及侧面积、全面积等基础知识。
3. 两个重要公式(1)侧面展开图的圆心角公式: 360⋅-=lrR θ 其中,l 为母线,r 和R 分别为上、下底面圆的半径,θ为侧面展开图的圆心角。
(2)侧面积公式:πl r R S )(侧面+=注:当r =0时,为圆锥;当R =r 时,为圆柱;当R ≠r 时,为圆台。
4. 复习处理本节知识的一般途径为“展、围、转、剖”等四种。
【典型例题】例1. 圆锥的侧面积为8π,其轴截面为一个等边三角形,求该轴截面的面积。
解析: 圆锥的轴截面为一个正三角形。
∴其母线长恰为其底面直径。
设母线长为x ,则底面半径为2x 由侧面S =πRl =ππ82=⋅x x,得x =4或-4(舍去) 344432=⨯=∴轴截面S 例2. 一个圆锥高为33,侧面展开图是个半圆,求(1)其母线与底面半径之比;(2)锥角的大小;(3)圆锥的表面积AhoBClr解析:本题的关键是要搞清楚圆锥的底面半径与母线之间的关系。
(如图) (1) 圆锥的侧面展开图恰为一个半圆 ∴2πr =πl ∴2=rl(2)2=rl∴AB =2OB ︒=∠∴30BAO ∴︒=∠60BAC 即锥角为︒60 (3)Rt ∆AOB 中, 2l =h 2+r 2又33,2==h r l63==∴l r , 底面侧面表面S S S +=∴=2r rl ππ+=3π(6+3)=27π例3. 如图矩形ABCD 中,AB =1,若直角三角形ABC 绕AB 旋转所得圆锥的侧面积和矩形ABCD 绕AB 旋转所得圆柱的侧面积相等,求BC 的长。
解析:∵S πAC BC S •==圆锥侧面1,S π22••CD BC S ==圆柱侧面 又S 1=S 2 ∴AC =2CD但ABCD 为矩形 ∴CD =AB =1 22==∴CD AC∴在Rt ∆ABC 中,BC =322=-AB AC ,即3=BC例4. 如图的圆柱底面上B 、E 处有两只小虫争D 处的零食,若甲从B 出发沿侧面的最短路程爬行,乙从E 处沿弧EC 和母线CD 方向爬行,已知它们的速度相同,且CD =4,底面圆的半径为1,E 为弧BC 的中点,问:哪一只小虫先得到零食?为什么?DCB(乙)(甲)ADCB(乙)(甲)(E )(B )(C )(D )(A )解析:应将空间的图形问题转化为平面上的图形问题来求解,如图为圆柱的侧面展开图,甲沿BD 走时,路程为最短,此时,BD =22216)1221(ππ+=••+CD ,乙走的路程为CE +CD =4+4π 44162ππ+<+ ∴甲先得到零食。
柱、锥、台体、圆的面积与体积公式(一)圆柱、圆锥、圆台的侧面积将侧面沿母线展开在平面上,则其侧面展开图的面积即为侧面面积。
1、圆柱的侧面展开图——矩形圆柱的侧面积2,,,S cl rl r l c π==圆柱侧其中为底面半径为母线长为底面周长2、圆锥的侧面展开图——扇形圆锥的侧面积1,,,2S cl rl r l c π==圆锥侧其中为底面半径为母线长为底面周长3、圆台的侧面展开图——扇环圆台的侧面积(二)直棱柱、正棱锥、正棱台的侧面积把侧面沿一条侧棱展开在一个平面上,则侧面展开图的面积就是侧面的面积。
1、柱的侧面展开图——矩形直棱柱的侧面积2、锥的侧面展开图——多个共点三角形正棱锥的侧面积3、正棱台的侧面展开图——多个等腰梯形正棱台的侧面积说明:这个公式实际上是柱体、锥体和台体的侧面积公式的统一形式 ①即锥体的侧面积公式;②c'=c 时即柱体的侧面积公式;(三)棱柱和圆柱的体积,V Sh h =柱体其中S 为柱体的底面积,为柱体的高斜棱柱的体积=直截面的面积×侧棱长(四)棱锥和圆锥的体积1,3V Sh h =锥体其中S 为锥体的底面积,为锥体的高(五)棱台和圆台的体积说明:这个公式实际上是柱、锥、台体的体积公式的统一形式:①0S=上时即为锥体的体积公式;②S上=S下时即为柱体的体积公式。
(六)球的表面积和体积公式(一)简单的组合几何体的表面积和体积——割补法的应用割——把不规则的组合几何体分割为若干个规则的几何体;补——把不规则的几何体通过添补一个或若干个几何体构造出一个规则的新几何体,如正四面体可以补成一个正方体,如图:四、考点与典型例题考点一几何体的侧面展开图例1. 有一根长为5cm,底面半径为1cm的圆柱形铁管,用一段铁丝在铁管上缠绕4圈,并使铁丝的两个端点落在圆柱的同一母线的两端A、D,则铁丝的最短长度为多少厘米?D CBA解:展开后使其成一线段ACcm =考点二求几何体的面积例2. 设计一个正四棱锥形的冷水塔顶,高是0.85m,底面的边长是1.5m,制造这种塔顶需要多少平方米铁板?(保留两位有效数字)ESO解:)m (40.313.15.1214S 2=⨯⨯⨯=⇒答:略。