考研数学二必背公式及知识点(自己精心总结整理)
- 格式:pdf
- 大小:1020.58 KB
- 文档页数:19

考研必背函数知识点归纳考研数学是许多考生在备考过程中的重点和难点之一。
函数作为数学中的核心概念,其知识点的掌握对于考研数学的复习至关重要。
以下是考研必背的函数知识点归纳:函数的定义与性质- 函数的定义:设A和B是两个非空集合,如果存在一个对应关系f,使得对于集合A中的每一个元素x,都有集合B中唯一确定的元素y与之对应,那么我们就称f:A→B为从集合A到集合B的一个函数,记作y=f(x)。
- 函数的三要素:定义域、值域、对应法则。
- 函数的表示方法:解析法、列表法、图像法。
- 函数的四则运算:加、减、乘、除。
函数的分类- 基本初等函数:幂函数、指数函数、对数函数、三角函数、反三角函数。
- 高等函数:有理函数、无理函数、分段函数等。
特殊函数的性质- 幂函数的性质:奇偶性、单调性、图像特征。
- 指数函数与对数函数的性质:单调性、图像特征、特殊值。
- 三角函数与反三角函数的性质:周期性、奇偶性、图像特征、和差化积公式、积化和差公式。
函数的极限- 极限的定义:数列极限、函数极限。
- 极限的性质:唯一性、有界性、保号性。
- 极限的运算法则:加、减、乘、除、复合函数的极限。
连续性与间断点- 连续性的定义:点连续、区间连续。
- 间断点的分类:第一类间断点、第二类间断点。
- 连续函数的性质:四则运算、复合函数的连续性。
导数与微分- 导数的定义:导数的几何意义、物理意义。
- 基本导数公式:幂函数、三角函数、指数函数、对数函数的导数。
- 高阶导数:二阶导数、三阶导数等。
- 微分的定义与性质:一阶微分、高阶微分。
函数的极值与最值- 极值的定义:局部极值、全局极值。
- 极值存在的条件:一阶导数为零、二阶导数的符号。
- 最值问题:闭区间上函数的最值。
函数的图像与变换- 函数图像的绘制:基本函数图像、复合函数图像。
- 函数图像的变换:平移、伸缩、对称变换。
结束语掌握上述函数知识点,对于考研数学的复习将大有裨益。
考生在复习时应注重理解函数的基本概念和性质,并通过大量练习来加深对函数运算、极限、导数、微分等知识点的掌握。

考研数学所有知识点总结考研数学是众多考生在研究生入学考试中面临的重要科目之一,涵盖了高等数学、线性代数和概率论与数理统计等多个领域。
以下将为大家详细梳理考研数学的所有重要知识点。
一、高等数学1、函数、极限与连续函数的概念,包括定义域、值域、单调性、奇偶性等。
极限的定义、性质和计算方法,如四则运算、洛必达法则等。
函数连续的定义、间断点的分类及判断。
2、一元函数微分学导数的定义、几何意义和物理意义。
基本初等函数的导数公式,导数的四则运算和复合函数求导法则。
微分的定义和计算。
利用导数研究函数的单调性、极值、最值和凹凸性。
3、一元函数积分学不定积分的概念、性质和基本积分公式。
换元积分法和分部积分法。
定积分的定义、性质和几何意义。
牛顿莱布尼茨公式。
利用定积分求平面图形的面积、旋转体的体积和曲线的弧长。
4、多元函数微分学多元函数的概念、定义域和值域。
偏导数的定义和计算,全微分的定义和计算。
多元复合函数和隐函数的求导法则。
多元函数的极值和条件极值。
5、多元函数积分学二重积分的定义、性质和计算方法,直角坐标和极坐标下的二重积分计算。
三重积分的定义和计算,柱坐标和球坐标下的三重积分计算。
曲线积分和曲面积分的概念、性质和计算方法。
6、无穷级数数项级数的收敛和发散的概念,正项级数的审敛法,交错级数的审敛法。
幂级数的概念、收敛半径和收敛区间的求法,幂级数的和函数。
函数展开成幂级数。
7、常微分方程常微分方程的基本概念,一阶常微分方程的求解方法,如可分离变量方程、齐次方程、一阶线性方程等。
二阶常系数线性微分方程的求解方法。
二、线性代数1、行列式行列式的定义、性质和计算方法。
行列式按行(列)展开定理。
2、矩阵矩阵的概念、运算(加法、数乘、乘法、转置)。
逆矩阵的定义、性质和求法。
矩阵的秩的定义和求法。
分块矩阵的运算。
3、向量向量的概念、线性运算和线性表示。
向量组的线性相关性的定义和判断方法。
向量组的秩和极大线性无关组。
4、线性方程组线性方程组的解的存在性和唯一性的判断。


考研数学考点与题型归类分析总结1高数部分1.1高数第一章《函数、极限、连续》求极限题最常用的解题方向:1.利用等价无穷小;2.利用洛必达法则型和∞∞型直接用洛必达法则∞0、0∞、∞1型先转化为型或∞∞型,再使用洛比达法则;3.利用重要极限,包括1sinlim=→xxx、ex xx=+→1)1(lim、exxx=+∞→)1(1lim;4.夹逼定理。
1.2高数第二章《导数与微分》、第三章《不定积分》、第四章《定积分》第三章《不定积分》提醒:不定积分⎰+=CxFdxxf)()(中的积分常数C容易被忽略,而考试时如果在答案中少写这个C会失一分。
所以可以这样加深印象:定积分⎰dxxf)(的结果可以写为F(x)+1,1指的就是那一分,把它折弯后就是⎰+=CxFdxxf)()(中的那个C,漏掉了C也就漏掉了这1分。
第四章《定积分及广义积分》解题的关键除了运用各种积分方法以外还要注意定积分与不定积分的差异——出题人在定积分题目中首先可能在积分上下限上做文章:对于⎰-a a dxxf)(型定积分,若f(x)是奇函数则有⎰-a a dxxf)(=0;若f(x)为偶函数则有⎰-a a dxxf)(=2⎰a dxxf)(;对于⎰20)(πdxxf型积分,f(x)一般含三角函数,此时用xt-=2π的代换是常用方法。
所以解这一部分题的思路应该是先看是否能从积分上下限中入手,对于对称区间上的积分要同时考虑到利用变量替换x=-u 和利用性质0=⎰-a a奇函数 、⎰⎰=-aa a2偶函数偶函数。
在处理完积分上下限的问题后就使用第三章不定积分的套路化方法求解。
这种思路对于证明定积分等式的题目也同样有效。
1.3 高数第五章《中值定理的证明技巧》用以下逻辑公式来作模型:假如有逻辑推导公式A ⇒E 、(A B)⇒C 、(C D E)⇒F ,由这样一组逻辑关系可以构造出若干难易程度不等的证明题,其中一个可以是这样的:条件给出A 、B 、D ,求证F 。

考研数学知识点总结归纳考研数学知识点第一章行列式1、行列式的定义2、行列式的性质3、特殊行列式的值4、行列式展开定理5、抽象行列式的计算第二章矩阵1、矩阵的定义及线性运算2、乘法3、矩阵方幂4、转置5、逆矩阵的概念和性质6、伴随矩阵7、分块矩阵及其运算8、矩阵的初等变换与初等矩阵9、矩阵的等价10、矩阵的秩第三章向量1、向量的概念及其运算2、向量的线性组合与线性表出3、等价向量组4、向量组的线性相关与线性无关5、极大线性无关组与向量组的秩6、内积与施密特正交化7、n维向量空间(数学一)第四章线性方程组1、线性方程组的克莱姆法则2、齐次线性方程组有非零解的判定条件3、非齐次线性方程组有解的判定条件4、线性方程组解的结构第五章矩阵的特征值和特征向量1、矩阵的特征值和特征向量的概念和性质2、相似矩阵的概念及性质3、矩阵的相似对角化4、实对称矩阵的特征值、特征向量及其相似对角矩阵第六章二次型1、二次型及其矩阵表示2、合同变换与合同矩阵3、二次型的秩4、二次型的标准型和规范型5、惯性定理6、用正交变换和配方法化二次型为标准型7、正定二次型及其判定考研数学必备知识点总结高等数学部分第一章函数、极限与连续1、函数的有界性2、极限的定义(数列、函数)3、极限的性质(有界性、保号性)4、极限的计算(重点)(四则运算、等价无穷小替换、洛必达法则、泰勒公式、重要极限、单侧极限、夹逼定理及定积分定义、单调有界必有极限定理)5、函数的连续性6、间断点的类型7、渐近线的计算第二章导数与微分1、导数与微分的定义(函数可导性、用定义求导数)2、导数的计算(“三个法则一个表”:四则运算、复合函数、反函数,基本初等函数导数表;“三种类型”:幂指型、隐函数、参数方程;高阶导数)3、导数的应用(切线与法线、单调性(重点)与极值点、利用单调性证明函数不等式、凹凸性与拐点、方程的根与函数的零点、曲率(数一、二))第三章中值定理1、闭区间上连续函数的性质(最值定理、介值定理、零点存在定理)2、三大微分中值定理(重点)(罗尔、拉格朗日、柯西)3、积分中值定理4、泰勒中值定理5、费马引理第四章一元函数积分学1、原函数与不定积分的定义2、不定积分的计算(变量代换、分部积分)3、定积分的定义(几何意义、微元法思想(数一、二))4、定积分性质(奇偶函数与周期函数的积分性质、比较定理)5、定积分的计算6、定积分的应用(几何应用:面积、体积、曲线弧长和旋转面的面积(数一、二),物理应用:变力做功、形心质心、液体静压力)7、变限积分(求导)8、广义积分(收敛性的判断、计算)第五章空间解析几何(数一)1、向量的运算(加减、数乘、数量积、向量积)2、直线与平面的方程及其关系3、各种曲面方程(旋转曲面、柱面、投影曲面、二次曲面)的求法第六章多元函数微分学1、二重极限和二元函数连续、偏导数、可微及全微分的定义2、二元函数偏导数存在、可微、偏导函数连续之间的关系3、多元函数偏导数的计算(重点)4、方向导数与梯度5、多元函数的极值(无条件极值和条件极值)6、空间曲线的切线与法平面、曲面的切平面与法线第七章多元函数积分学(除二重积分外,数一)1、二重积分的`计算(对称性(奇偶、轮换)、极坐标、积分次序的选择)2、三重积分的计算(“先一后二”、“先二后一”、球坐标)3、第一、二类曲线积分、第一、二类曲面积分的计算及对称性(主要关注不带方向的积分)4、格林公式(重点)(直接用(不满足条件时的处理:“补线”、“挖洞”),积分与路径无关,二元函数的全微分)5、高斯公式(重点)(不满足条件时的处理(类似格林公式))6、斯托克斯公式(要求低;何时用:计算第二类曲线积分,曲线不易参数化,常表示为两曲面的交线)7、场论初步(散度、旋度)第八章微分方程1、各类微分方程(可分离变量方程、齐次方程、一阶线性微分方程、伯努利方程(数一、二)、全微分方程(数一)、可降阶的高阶微分方程(数一、二)、高阶线性微分方程、欧拉方程(数一)、差分方程(数三))的求解2、线性微分方程解的性质(叠加原理、解的结构)3、应用(由几何及物理背景列方程)第九章级数(数一、数三)1、收敛级数的性质(必要条件、线性运算、“加括号”、“有限项”)2、正项级数的判别法(比较、比值、根值,p级数与推广的p级数)3、交错级数的莱布尼兹判别法4、绝对收敛与条件收敛5、幂级数的收敛半径与收敛域6、幂级数的求和与展开7、傅里叶级数(函数展开成傅里叶级数,狄利克雷定理)线性代数部分第一章行列式1、行列式的定义2、行列式的性质3、特殊行列式的值4、行列式展开定理5、抽象行列式的计算第二章矩阵1、矩阵的定义及线性运算2、乘法3、矩阵方幂4、转置5、逆矩阵的概念和性质6、伴随矩阵7、分块矩阵及其运算8、矩阵的初等变换与初等矩阵9、矩阵的等价10、矩阵的秩第三章向量1、向量的概念及其运算2、向量的线性组合与线性表出3、等价向量组4、向量组的线性相关与线性无关5、极大线性无关组与向量组的秩6、内积与施密特正交化7、n维向量空间(数学一)第四章线性方程组1、线性方程组的克莱姆法则2、齐次线性方程组有非零解的判定条件3、非齐次线性方程组有解的判定条件4、线性方程组解的结构第五章矩阵的特征值和特征向量1、矩阵的特征值和特征向量的概念和性质2、相似矩阵的概念及性质3、矩阵的相似对角化4、实对称矩阵的特征值、特征向量及其相似对角矩阵第六章二次型1、二次型及其矩阵表示2、合同变换与合同矩阵3、二次型的秩4、二次型的标准型和规范型5、惯性定理6、用正交变换和配方法化二次型为标准型7、正定二次型及其判定概率论与数理统计部分第一章随机事件和概率1、随机事件的关系与运算2、随机事件的运算律3、特殊随机事件(必然事件、不可能事件、互不相容事件和对立事件)4、概率的基本性质5、随机事件的条件概率与独立性6、五大概率计算公式(加法、减法、乘法、全概率公式和贝叶斯公式)7、全概率公式的思想8、概型的计算(古典概型和几何概型)第二章随机变量及其分布1、分布函数的定义2、分布函数的充要条件3、分布函数的性质4、离散型随机变量的分布律及分布函数5、概率密度的充要条件6、连续型随机变量的性质7、常见分布(0-1分布、二项分布、几何分布、超几何分布、泊松分布、均匀分布、指数分布、正态分布)8、随机变量函数的分布(离散型、连续型)第三章多维随机变量及其分布1、二维离散型随机变量的三大分布(联合、边缘、条件)2、二维连续型随机变量的三大分布(联合、边缘和条件)3、随机变量的独立性(判断和性质)4、二维常见分布的性质(二维均匀分布、二维正态分布)5、随机变量函数的分布(离散型、连续型)第四章随机变量的数字特征1、期望公式(一个随机变量的期望及随机变量函数的期望)2、方差、协方差、相关系数的计算公式3、运算性质(期望、方差、协方差、相关系数)4、常见分布的期望和方差公式第五章大数定律和中心极限定理1、切比雪夫不等式2、大数定律(切比雪夫大数定律、辛钦大数定律、伯努利大数定律)3、中心极限定理(列维—林德伯格定理、棣莫弗—拉普拉斯定理)第六章数理统计的基本概念1、常见统计量(定义、数字特征公式)2、统计分布3、一维正态总体下的统计量具有的性质4、估计量的评选标准(数学一)5、上侧分位数(数学一)第七章参数估计1、矩估计法2、最大似然估计法3、区间估计(数学一)第八章假设检验(数学一)1、显著性检验2、假设检验的两类错误3、单个及两个正态总体的均值和方差的假设检验考研数学复习之拿高分方法一、理性分析三个组成部分,各个击破我们知道数学整个试卷的组成部分是:高数82分+线代34分+概率论34分;很明显微积分占了绝大部分;另外概率论里面很多题目要用到微积分的工具,实际上微积分的分数比82分要高,应该是能到100分左右。
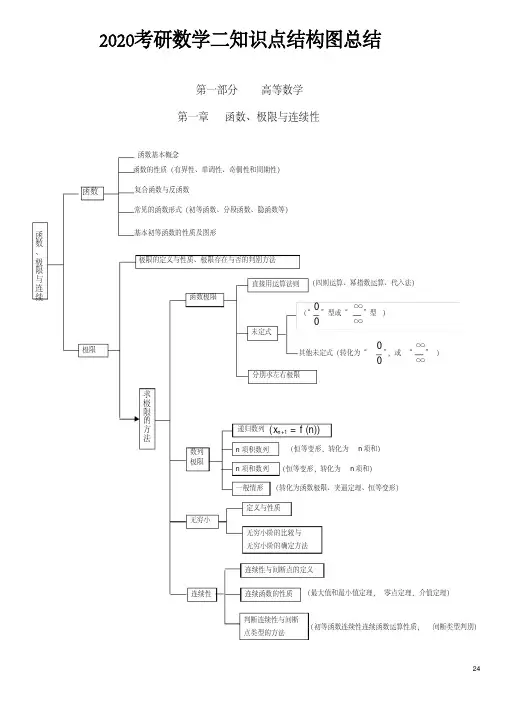
242020考研数学二知识点结构图总结第一部分高等数学第一章函数、极限与连续性
函数、极限与连续
函数的性质(有界性、单调性、奇偶性和周期性)复合函数与反函数常见的函数形式(初等函数、分段函数、隐函数等)
连续性与间断点的定义连续函数的性质判断连续性与间断点类型的方法(初等函数连续性连续函数运算性质,间断类型判别)极限的定义与性质、极限存在与否的判别方法未定式(“00”型或“∞∞”型)其他未定式(转化为“00”,或“∞∞”)直接用运算法则分别求左右极限(四则运算、幂指数运算、代入法)函数极限数列极限递归数列1(())nxfn+=n项积数列(恒等变形,转化为n项和)n项和数列(恒等变形,转化为n项和)一般情形(转化为函数极限、夹逼定理、恒等变形)求极限的方法连续性
极限基本初等函数的性质及图形无穷小定义与性质无穷小阶的比较与无穷小阶的确定方法
(最大值和最小值定理,零点定理,介值定理)
函数函数基本概念25
第二章导数与微分平面曲线的切线与法线平面曲线的曲率、曲率圆与曲率半径判断函数的凹凸性某些物理量的描述
定义法分段函数求导法幂指数函数()()gxfx求导法反函数求导法变限积分求导法导数与微分的四则运算法则复合函数求导法由复合函数求导法导出的微分法则定义几何意义与物理意义相互关系可微?可导?连续奇偶函数与周期函数的导数性质导数、微分与可微概念?求导方法基本导数表微分法则隐函数求导法参数式求导法求某些n阶导数表达式的方法函数的可导性及导函数的连续性的判断简单应用导数与微分26
第三章不定积分几何意义与物理意义原函数的存在性
不定积分
原函数不定积分
凑微分法常用的变量代换
基本积分表积分计算基本概念基本性质()d()dkfxxkfxx=∫∫F()dF()xxxc′=+∫()d()fxxfx′??=??∫定义积分法则
分项积分法
换元积分法分段积分法
分部积分法有理函数,三角函数有理式和简单无理函数的积分
()())d()d()dfxgxxfxxgxx+=+∫∫∫

数学知识点背诵高数部分1. 导数公式22(tan )sec (cot )csc (sec )sec tan (csc )csc cot x xx xx x x x x x'='=-'=⋅'=-⋅22(arcsin )(arccos )1(arctan )11(cot )1x x x x arc x x '='='=+'=-+2. 积分公式2222tan ln cos cot ln sin sec ln sec tan csc ln csc cot sec tan cos csc cot sin sec tan sec csc cot csc xdx x C xdx x Cxdx x x C xdx x x Cdx xdx x C x dx xdx x Cx x xdx x Cx xdx x C=-+=+=++=-+==+==-+⋅=+⋅=-+⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰2222221arctan 1ln 21ln 2ln(arcsin dx xC a x a a dx x aC x a a x a dx a xC a x a a x x CxC a=++-=+-++=+--=+=+⎰⎰⎰222ln(2ln 2arcsin 2a x Ca x C a x Ca=+=-++=++22201sin cos nn n n n I xdx xdx I nππ--===⎰⎰3. 和差化积sin sin 2sincos22sin sin 2cos sin22cos cos 2cos cos22cos cos 2sin sin22αβαβαβαβαβαβαβαβαβαβαβαβ+-+=+--=+-+=+--=-4. 积化和差[][][][]1sin cos sin()sin()21cos sin sin()sin()21cos cos cos()cos()21sin sin cos()cos()2αβαβαβαβαβαβαβαβαβαβαβαβ=++-=+--=++-=-+-- 5. 万能公式22tan2sin 1tan 2ααα=+ 221t a n2c o s 1t a n 2ααα-=+ 22t a n2t a n 1t a n2ααα=- 6. 半角公式221cos sin 221cos cos 22αααα-=+= 21c o s t a n 21c o s s i n 1c o s t a n 21c o s s i nαααααααα-=+-==+7. 三倍角公式3332sin 33sin 4sin cos34cos 3cos 3tan tan tan 313tan αααααααααα=-=--=- 8. 三角函数关系图sin costan 1cot sec csc↔↔↔⊗↔↔↔↔↔↔⊗⊗↔↔↔..1.a b c ⊗说明:六边形每个顶点等于两相邻顶点乘积三条对角线上,两端点相乘等于标记的三角形,上面的平方和等于下面的平方9. 等价无穷小33333333222201sin ()61arcsin ()61tan ()31arctan ()31ln(1)()21cos 1()2x x x x o x x x x o x x x x o x x x x o x x x x o x x x o x →=-+=++=++=-++=-+=-+时2011ln 11cos 2(1)1x x x e x a x a x xx x αα→---+-时10. 华里士公式等华里士公式:2200131,222sin cos 132,123n nn n n n n xdx xdx n n n n n πππ--⎧⋅⋅⎪⎪-==⎨--⎪⋅⎪-⎩⎰⎰为正的偶数为大于的奇数20sin 2sin nn xdx xdx ππ=⎰⎰2002c o s ,c o s 0,n nxdx n xdx n ππ⎧⎪=⎨⎪⎩⎰⎰为偶数为奇数2220004sin ,sin =cos 0,n n nxdx n xdx xdx n πππ⎧⎪=⎨⎪⎩⎰⎰⎰为偶数为奇数()()220sin cos f x dx f x dx ππ=⎰⎰ ()()00sin cos f x dx f x dx ππ≠⎰⎰()()()20sin sin sin 2xf x dx f x dx f x dx πππππ==⎰⎰⎰11. 函数展开为幂级数20201+()!2!1(1)1(1)(11)1n nxn n n n nn x x x e x x n n x x x x x x ∞=∞===++++-∞<<+∞=-=-+-+-+-<<+∑∑!20234111213572122011(11)1ln(1)(1)(1)(11)234sin (1)(1)()(21)!3!5!7!(21)!cos (1)1(2)!2!n n n n nn n n n n nnn n nn x x x x x x x x x x x x x x n nx x x x x x x x n n x x x n ∞=∞--=++∞=∞===+++++-<<-+=-=-+-++-+-<≤=-=-+-++-+-∞<<+∞++=-=-+∑∑∑∑()(][]4622(1)()4!6!(2)!(1)(1)(1)(1)12!!(1-1,1;10-1,1;0-1,1)nn nx x x x n n x x x x n αααααααααα-++-+-∞<<+∞---++=+++++≤--<<>时,收敛域为时,收敛域为时,收敛域为12. 幂级数的和函数1211121121212112220(1)11(1)1(1)(1)(1)(1)(1)1(1)1k nn k n n n n n n n n n n n n n n n n n n cx cx x x x nx x x x x x nx x nx x x x nx x nx x x n n x x x x ∞=∞∞-==∞∞-==∞∞+-==∞∞∞-====<-''⎛⎫⎛⎫===< ⎪ ⎪--⎝⎭⎝⎭==<-==<-''''''⎛⎫⎛⎫⎛⎫-=== ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭∑∑∑∑∑∑∑∑∑∑3110001112(1)(1)1ln(1)(11)1n x x x n n n n n x x x t dt t dt dt x x n t ∞∞∞--====<-⎛⎫====---≤< ⎪-⎝⎭∑∑∑⎰⎰⎰13. 狄利克雷收敛定理设()f x 是以2l 为周期的可积函数,如果在[],l l -上()f x 满足: 1)连续或只有有限个第一类间断点; 2)只有有限个极值点;则()f x 的傅里叶级数处处收敛,记其和函数为()S x ,则()01cos sin 2n n n a n x n x S x a b l l ππ∞=⎛⎫=++ ⎪⎝⎭∑,且()()()()()(),00,200,2f x x f x f x S x x f l f l x ⎧⎪⎪-++⎪=⎨⎪⎪-++-⎪⎩为连续点为第一类间断点为端点 14. 周期为2l 的周期函数的傅里叶级数设周期为2l 的周期函数()f x 满足狄利克雷收敛定理的条件,则它的傅里叶级数为()()01cos sin 2n n n a n x n x f x S x a b l l ππ∞=⎛⎫=++ ⎪⎝⎭∑其中系数n a 和n b 分别为:()()1cos (0,1,2,)1sin (1,2,3,)l n l l n l n x a f x dx n l l n x b f x dx n l l ππ--⎧==⎪⎪⎨⎪==⎪⎩⎰⎰ (1)将普通周期函数()f x 在[],l l -上展开为傅里叶级数: 展开系数为()()()01,1cos ,(1,2,3,)1sin ,(1,2,3,)l l l n l l n la f x dx l n x a f x dx n l l n xb f x dx n l l ππ---⎧=⎪⎪⎪==⎨⎪⎪==⎪⎩⎰⎰⎰ (2)将奇偶周期函数()f x 在[],l l -上展开为傅里叶级数:当()f x 为奇函数时,展开为正弦级数()000,0,(1,2,3,)2sin ,(1,2,3,)n l n a a n n x b f x dx n l l π⎧⎪=⎪==⎨⎪⎪==⎩⎰当()f x 为偶函数时,展开为余弦级数()()0002,2cos ,(1,2,3,)0,(1,2,3,)l l nn a f x dx l n x a f x dx n l l b n π⎧=⎪⎪⎪==⎨⎪==⎪⎪⎩⎰⎰ (3)将非对称区间[]0,l 上的函数()f x 展开为正弦级数或余弦级数:将[]0,l 上的函数()f x ,根据要求作奇延拓(若要求展开为正弦级数)或偶延拓(若要求展开为余弦函数),得到[],l l -上的奇函数或偶函数,再根据(2)中的方式展开。

考研数学复习有些概率计算的公式在考研数学三中,参数估计占数理统计的一多半内容,所以参数估计是重点。
为大家精心准备了考研数学复习概率计算的公式指导,欢送大家前来阅读。
五大公式包括减法公式、加法公式、乘法公式、全概率公式、贝叶斯公式。
1、减法公式,P(A-B)=P(A)-P(AB)。
此公式事件关系中的差事件,再结合概率的可列可加性总结出的公式。
2、加法公式,P(A+B)=P(A)+P(B)-P(AB)。
此公式于事件关系中的和事件,同样结合概率的可列可加性总结出来。
学生还应掌握三个事件相加的加法公式。
以上两个公式,在应用当中,有时要结合文氏图来解释会更清楚明白,同时这两个公式在考试中,更多的会出现在填空题当中。
所以记住公式的形式是根本要求。
3、乘法公式,是由条件概率公式变形得到,考试中较多的出现在计算题中。
在复习过程中,局部分不清楚时候用条件概率来求,什么时候用积事件概率来求。
比方“第一次抽到红球,第二次抽到黑球”时,因为第一次抽到红球也是事件,所以要考虑它的概率,这时候用积事件概率来求;如果“在第一次抽到红球的情况下,第二次抽到黑球的概率”,这时候因为抽到了红球,它已经是一个确定的事实,所以这时候不用考虑抽红球的概率,直接用条件概率,求第二次取到黑球的概率即可。
4、全概率公式5、贝叶斯公式以上两个公式是五大公式极为重要的两个公式。
结合起来比拟容易理解。
首先,这两个公式首先背景是相同的,即,完成一件事情在逻辑或时间上是需要两个步骤的,通常把第一个步骤称为原因。
其次,如果是“由因求果”的问题用全概率公式;是“由果求因”的问题用贝叶斯公式。
例如;买零件,一个零件是由A、B、C三个厂家生产的,分别次品率是a%,b%,c%,现在求买到次品的概率时,就要用全概率公式;假设买到次品了,问是A厂生产的概率,这就要用贝叶斯公式了。
这样我们首先分清楚了什么时候用这两个公式。
那么,在应用过程中,我们要注意的问题就是,如何划分完备事件组。

考研数学二的考试范围有哪些快速了解下引言概述:在申请考研时,数学二是很多同学选择的考试科目之一。
了解考研数学二的考试范围对于备考具有重要意义。
本文将对考研数学二的考试范围进行详细介绍,以便考生快速了解。
正文内容:第一大点:数学分析1.实数与函数- 实数集及其性质- 函数的基本概念与性质- 函数的极限与连续2.级数- 数项级数- 幂级数- Fourier级数3.极限- 极限存在准则- 极限与连续的关系- 罗尔中值定理与柯西中值定理4.微分学- 导数的定义与几何意义- 微分中值定理- 函数的单调性与曲线的凹凸性5.积分学- 定积分与不定积分的概念- 积分中值定理- 常微分方程第二大点:线性代数1.矩阵与行列式- 矩阵及其运算- 矩阵的逆与秩- 行列式的性质与求解2.线性方程组- 高斯消元法- 线性方程组的解的结构- 向量空间及其性质3.特征值和特征向量- 特征值与特征向量的定义与性质 - 对角化与相似矩阵- 矩阵的谱分解4.线性变换- 线性变换的定义与性质- 线性变换的矩阵表示- 线性变换的特征值与特征向量5.内积空间- 内积的定义与性质- 正交与正交补- 最小二乘问题第三大点:概率论与数理统计1.概率论基础- 随机试验与事件- 频率与概率- 条件概率与独立性2.随机变量及其分布- 随机变量的概念- 离散型和连续型随机变量 - 二维随机变量及其分布3.随机变量的数字特征- 数学期望与方差- 协方差与相关系数- 大数定律与中心极限定理4.常用概率分布- 二项分布- 正态分布- 指数分布5.参数估计与假设检验- 点估计与区间估计- 假设检验的基本方法- 卡方检验与相关分析第四大点:离散数学1.集合论与图论- 集合的基本概念与运算 - 图论的基本概念与运算 - 图的连通性与匹配2.逻辑与命题- 命题公式与合取范式- 命题逻辑基本原理- 谓词逻辑3.代数系统与组合数学- 代数系统的基本概念- 置换群与对称群- 组合数学的基本概念与方法4.图的着色与平面图- 图的着色问题- 平面图与图的可平面性- 树与生成树5.算法与应用- 算法的基本概念与设计方法 - 整数因子分解算法- 随机模拟与蒙特卡罗方法第五大点:数学分析的应用1.微分方程- 常微分方程的基本概念- 一阶线性微分方程- 高阶线性微分方程2.泛函分析- 范数空间与内积空间- 空间的完备性与紧性- 线性算子与相容定理3.积分方程- 第一类和第二类Volterra积分方程 - 第一类和第二类Fredholm积分方程 - 求解方法与应用4.辅助工具- 无穷级数的收敛性判断- 重积分与换元积分法- 综合应用举例5.综合应用举例- 求解物理问题的数学模型- 求解工程问题的数学模型- 求解经济问题的数学模型总结:本文对考研数学二的考试范围进行了全面且细致的介绍,从数学分析、线性代数、概率论与数理统计、离散数学,到数学分析的应用,共包含了五大点的内容。

全国硕士研究生统一入学考试数学公式大全高等数学公式导数公式:基本积分表:ax x a a a ctgx x x tgx x x x ctgx x tgx a x x ln 1)(log ln )(csc )(csc sec )(sec csc )(sec )(22='='⋅-='⋅='-='='222211)(11)(11)(arccos 11)(arcsin x arcctgx x arctgx x x x x +-='+='--='-='⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰+±+=±+=+=+=+-=⋅+=⋅+-==+==Ca x x a x dx C shx chxdx C chx shxdx Ca a dx a Cx ctgxdx x Cx dx tgx x Cctgx xdx x dx C tgx xdx x dx xx)ln(ln csc csc sec sec csc sin sec cos 22222222C axx a dx C x a xa a x a dx C a x ax a a x dx C a xarctg a x a dx Cctgx x xdx C tgx x xdx Cx ctgxdx C x tgxdx +=-+-+=-++-=-+=++-=++=+=+-=⎰⎰⎰⎰⎰⎰⎰⎰arcsin ln 21ln 211csc ln csc sec ln sec sin ln cos ln 22222222⎰⎰⎰⎰⎰++-=-+-+--=-+++++=+-===-Cax a x a x dx x a Ca x x a a x x dx a x Ca x x a a x x dx a x I nn xdx xdx I n n nn arcsin 22ln 22)ln(221cos sin 2222222222222222222222ππ三角函数的有理式积分:222212211cos 12sin u dudx x tg u u u x u u x +==+-=+=, , , 一些初等函数: 两个重要极限:三角函数公式: ·诱导公式:·和差角公式: ·和差化积公式:2sin2sin 2cos cos 2cos2cos 2cos cos 2sin2cos 2sin sin 2cos2sin2sin sin βαβαβαβαβαβαβαβαβαβαβαβα-+=--+=+-+=--+=+αββαβαβαβαβαβαβαβαβαβαβαctg ctg ctg ctg ctg tg tg tg tg tg ±⋅=±⋅±=±=±±=±1)(1)(sin sin cos cos )cos(sin cos cos sin )sin( xxarthx x x archx x x arshx e e e e chx shx thx e e chx e e shx x xxx xx xx -+=-+±=++=+-==+=-=----11ln21)1ln(1ln(:2:2:22)双曲正切双曲余弦双曲正弦...590457182818284.2)11(lim 1sin lim 0==+=∞→→e xxx x x x·倍角公式:·半角公式:ααααααααααααααααααcos 1sin sin cos 1cos 1cos 12cos 1sin sin cos 1cos 1cos 122cos 12cos 2cos 12sin -=+=-+±=+=-=+-±=+±=-±=ctg tg·正弦定理:R CcB b A a 2sin sin sin === ·余弦定理:C ab b a c cos 2222-+= ·反三角函数性质:arcctgx arctgx x x -=-=2arccos 2arcsin ππ高阶导数公式——莱布尼兹(Leibniz )公式:)()()()2()1()(0)()()(!)1()1(!2)1()(n k k n n n n nk k k n k n n uv v u k k n n n v u n n v nu v u v u C uv +++--++''-+'+==---=-∑中值定理与导数应用:拉格朗日中值定理。

考研教学二教材下载电子教材我们讲义共写了八章,数学一的考生全部要学,而其它考生只需要其中的一部分。
根据共同需要的内容先讲的原则,讲课内容与顺序安排如下:第一章 函数、极限、连续 (全体) 第二章 一元函数微分学(全体) 第三章 一元函数积分学(全体) 第六章多元函数微分学 (全体) 第七章 §7.1 二重积分 (全体) 第四章 §4.1 一阶微分方程§4.3 微分方程的应用(数学四考生结束)§4.2 高阶微分方程(数学二考生结束)第八章 无穷级数 (数学三考生结束)第五章 向量代数与空间解析几何 第七章 §7.2 三重积分 §7.3 曲线积分 §7.4 曲面积分 数学一全部内容结束第一章 函数、极限、连续§1.1 函数(甲) 内容要点一、函数的概念1. 定义)(x f y =,I x ∈x 为自变量,y 为因变量或称为函数值y x f→: 为对应关系自变量在定义域里面取值的时候,所有的函数值的全体就称为值域。
口诀(1):函数概念五要素;对应关系最核心。
2. 分段函数(考研中用得很多)例1: 1,1,13)(2≥<⎩⎨⎧+=x x x x x f例2:0,0,<≥⎩⎨⎧-=x x x x x例3:1,10,0,),,max(3232>≤<≤⎪⎩⎪⎨⎧=x x x xx x x x x口诀(2):分段函数分段点;左右运算要先行。
3.反函数 例:2x y = 的反函数 y x ±=由于不单值,所以要看作 y x = 和yx -=,它们的图像与2x y =一致。
如果改变符号,写成x y =和 x y -=,那么它们的图像要变。
4.隐函数0),(=y x F 确定y 与x 的函数关系 有些隐函数能化为显函数,例:122=+y x ,21x y -=和21x y --=。
另外有些隐函数则不能化为显函数。
考研数学核心知识点总结汇编考研数学是众多考生面临的一大挑战,掌握核心知识点是取得好成绩的关键。
以下是对考研数学核心知识点的详细总结。
一、高等数学1、函数、极限与连续函数的概念、性质(奇偶性、周期性、单调性等)需要熟练掌握。
极限的计算方法,如利用等价无穷小替换、洛必达法则等是重点。
连续的定义及间断点的类型判断也是常考内容。
2、一元函数微分学导数的定义、几何意义及物理意义要清晰。
求导法则,包括四则运算、复合函数求导等必须熟练运用。
微分中值定理(罗尔定理、拉格朗日中值定理、柯西中值定理)是证明题的重要工具。
函数的单调性、极值、凹凸性的判断方法要牢记。
3、一元函数积分学不定积分的计算方法,如换元法、分部积分法等要多练习。
定积分的定义、性质及计算,利用定积分求平面图形的面积、旋转体的体积等应用问题是常见考点。
4、多元函数微分学多元函数的偏导数、全微分的概念及计算。
多元函数极值的判定条件,条件极值与拉格朗日乘数法的应用。
5、多元函数积分学二重积分的计算方法,包括直角坐标法、极坐标法。
三重积分的计算,利用柱坐标、球坐标进行转换。
曲线积分与曲面积分的概念、性质及计算。
6、无穷级数数项级数的敛散性判别,正项级数的比较判别法、比值判别法,交错级数的莱布尼茨判别法。
幂级数的收敛半径、收敛区间的求法,函数展开成幂级数。
7、常微分方程一阶微分方程的求解方法,如可分离变量方程、齐次方程、一阶线性方程。
二阶常系数线性微分方程的解法,分清齐次与非齐次的情况。
二、线性代数1、行列式行列式的性质与计算,包括展开法则、三角化法等。
2、矩阵矩阵的运算(加法、乘法、数乘),矩阵的逆、秩的概念及求法。
分块矩阵的运算及应用。
3、向量向量组的线性相关性判断,极大线性无关组的求法。
向量空间的基本概念。
4、线性方程组线性方程组解的存在性、唯一性判断,求解线性方程组的方法(高斯消元法)。
5、矩阵的特征值与特征向量特征值与特征向量的定义及求法,相似矩阵的性质及矩阵可相似对角化的条件。
考研数学基础知识点梳理(高数篇) 第一章函数、极限与连续1、函数的有界性2、极限的定义(数列、函数)3、极限的性质(有界性、保号性)4、极限的计算(重点)(四则运算、等价无穷小替换、洛必达法则、泰勒公式、重要极限、单侧极限、夹逼定理及定积分定义、单调有界必有极限定理)5、函数的连续性6、间断点的类型7、渐近线的计算第二章导数与微分1、导数与微分的定义(函数可导性、用定义求导数)2、导数的计算(“三个法则一个表”:四则运算、复合函数、反函数,基本初等函数导数表;“三种类型”:幂指型、隐函数、参数方程;高阶导数)3、导数的应用(切线与法线、单调性(重点)与极值点、利用单调性证明函数不等式、凹凸性与拐点、方程的根与函数的零点、曲率(数一、二)) 第三章中值定理1、闭区间上连续函数的性质(最值定理、介值定理、零点存在定理)2、三大微分中值定理(重点)(罗尔、拉格朗日、柯西)3、积分中值定理4、泰勒中值定理5、费马引理第四章一元函数积分学1、原函数与不定积分的定义2、不定积分的计算(变量代换、分部积分)3、定积分的定义(几何意义、微元法思想(数一、二))4、定积分性质(奇偶函数与周期函数的积分性质、比较定理)5、定积分的计算6、定积分的应用(几何应用:面积、体积、曲线弧长和旋转面的面积(数一、二),物理应用:变力做功、形心质心、液体静压力)7、变限积分(求导)8、广义积分(收敛性的判断、计算)第五章空间解析几何(数一)1、向量的运算(加减、数乘、数量积、向量积)2、直线与平面的方程及其关系3、各种曲面方程(旋转曲面、柱面、投影曲面、二次曲面)的求法第六章多元函数微分学1、二重极限和二元函数连续、偏导数、可微及全微分的定义2、二元函数偏导数存在、可微、偏导函数连续之间的关系3、多元函数偏导数的计算(重点)4、方向导数与梯度5、多元函数的极值(无条件极值和条件极值)6、空间曲线的切线与法平面、曲面的切平面与法线第七章多元函数积分学(除二重积分外,数一)1、二重积分的计算(对称性(奇偶、轮换)、极坐标、积分次序的选择)2、三重积分的计算(“先一后二”、“先二后一”、球坐标)3、第一、二类曲线积分、第一、二类曲面积分的计算及对称性(主要关注不带方向的积分)4、格林公式(重点)(直接用(不满足条件时的处理:“补线”、“挖洞”),积分与路径无关,二元函数的全微分)5、高斯公式(重点)(不满足条件时的处理(类似格林公式))6、斯托克斯公式(要求低;何时用:计算第二类曲线积分,曲线不易参数化,常表示为两曲面的交线)7、场论初步(散度、旋度)第八章微分方程1、各类微分方程(可分离变量方程、齐次方程、一阶线性微分方程、伯努利方程(数一、二)、全微分方程(数一)、可降阶的高阶微分方程(数一、二)、高阶线性微分方程、欧拉方程(数一)、差分方程(数三))的求解2、线性微分方程解的性质(叠加原理、解的结构)3、应用(由几何及物理背景列方程)第九章级数(数一、数三)1、收敛级数的性质(必要条件、线性运算、“加括号”、“有限项”)2、正项级数的判别法(比较、比值、根值,p级数与推广的p级数)3、交错级数的莱布尼兹判别法4、绝对收敛与条件收敛5、幂级数的收敛半径与收敛域6、幂级数的求和与展开7、傅里叶级数(函数展开成傅里叶级数,狄利克雷定理)。
数学二考研证明题总结在数学二考研中,证明题是非常重要的一部分。
本文将从微积分证明题、线性代数证明题、概率论与数理统计证明题、解析几何证明题、数学分析证明题五个方面进行总结。
一、微积分证明题微积分证明题是数学二考研中非常重要的一部分,主要涉及极限、导数、积分等知识点。
在证明微积分题目时,需要注意以下几点:1. 对于极限的证明题,要掌握好各种极限的求法,如等价无穷小替换、洛必达法则、泰勒公式等。
2. 对于导数的证明题,要掌握好各种导数的求法,如链式法则、乘法法则、高阶导数等。
3. 对于积分的证明题,要掌握好各种积分的求法,如定积分、反常积分等。
二、线性代数证明题线性代数证明题主要涉及矩阵、向量、线性方程组等知识点。
在证明线性代数题目时,需要注意以下几点:1. 对于矩阵的证明题,要掌握好各种矩阵的计算方法,如行列式、逆矩阵、特征值等。
2. 对于向量的证明题,要掌握好各种向量的计算方法,如向量的加法、减法、数乘等。
3. 对于线性方程组的证明题,要掌握好各种线性方程组的解法,如高斯消元法、逆矩阵法等。
三、概率论与数理统计证明题概率论与数理统计证明题主要涉及随机事件、概率分布、大数定律等知识点。
在证明概率论与数理统计题目时,需要注意以下几点:1. 对于随机事件的证明题,要掌握好各种随机事件的计算方法,如互斥事件、独立事件、对立事件等。
2. 对于概率分布的证明题,要掌握好各种概率分布的计算方法,如二项分布、泊松分布、正态分布等。
3. 对于大数定律的证明题,要掌握好各种大数定律的证明方法,如切比雪夫大数定律、伯努利大数定律等。
四、解析几何证明题解析几何证明题主要涉及平面解析几何和空间解析几何的知识点。
在证明解析几何题目时,需要注意以下几点:1. 对于平面解析几何的证明题,要掌握好各种曲线的方程表示方法和平面曲线的位置关系。
2. 对于空间解析几何的证明题,要掌握好各种空间曲线和曲面的方程表示方法和空间曲线曲面的位置关系。
高等数学(数二)整理人:刘超说明:本文只适合内部流传,严禁外传,来源于网各个专家分析,其中线性代数为本人的心得感悟理解,另附网上9个大题的猜测:必考题型及2013可能会考的题型;及李永乐,王式安的基础导学班题型分析。
一.重点知识标记高等数学科目大纲章节知识点题型重要度等级高等数学第一章函数、极限、连续1 .等价无穷小代换、洛必达法则、泰勒展开式求函数的极限★★★★★2 .函数连续的概念、函数间断点的类型3 .判断函数连续性与间断点的类型★★★第二章一元函数微分学1 .导数的定义、可导与连续之间的关系按定义求一点处的导数,可导与连续的关系★★★★2 .函数的单调性、函数的极值讨论函数的单调性、极值★★★★3.闭区间上连续函数的性质、罗尔定理、拉格朗日中值定理、柯西中值定理和泰勒定理微分中值定理及其应用★★★★★第三章一元函数积分学1 .积分上限的函数及其导数变限积分求导问题★★★★★2 .有理函数、三角函数有理式、简单无理函数的积分计算被积函数为有理函数、三角函数有理式、简单无理函数的不定积分和定积分★★第四章多元函数微分学1 .隐函数、偏导数、的存在性以及它们之间的因果关系2 .函数在一点处极限的存在性,连续性,偏导数的存在性,全微分存在性与偏导数的连续性的讨论与它们之间的因果关系★★3 .多元复合函数、隐函数的求导法求偏导数,全微分★★★★★第五章多元函数积分学1. 二重积分的概念、性质及计算2.二重积分的计算及应用★★第六章常微分方程1.一阶线性微分方程、齐次方程,2.微分方程的简单应用,用微分方程解决一些应用问题★★★★一、函数、极限、连续部分:极限的运算法则、极限存在的准则(单调有界准则和夹逼准则)、未定式的极限、主要的等价无穷小、函数间断点的判断以及分类,还有闭区间上连续函数的性质(尤其是介值定理),这些知识点在历年真题中出现的概率比较高,属于重点内容,但是很基础,不是难点,因此这部分内容一定不要丢分。
[基础知识]n -b n =(a -b)( a n−1+a n−2b+…+ab n−2+b n−1) ( n 为正偶数时)a n -b n =(a +b)( a n−1-a n−2b+…+ab n−2-b n−1) ( n 为正奇数时)a n +b n =(a +b)( a n−1-a n−2b+…-ab n−2+b n−1)+b)n =∑C n k a k bn−kn k=0(1) a,b 位实数,则○12|ab |≤a 2+b 2;○2|a ±b |≤|a |+|b |;○3|a |−|b |≤|a −b |. (2) a 1,a 2,…,a n >0, 则 ○1a 1+a 2+⋯+a n n ≥√a 1a 2⋯a n n<[x]≤x和差化积;积化和差(7):sin α+sin β=2(sin α+β2)(cosα−β2) sin αcos β=12(sinα+β2+cosα−β2)sin α-sin β=2(cosα+β2)(sinα−β2) cos αcos β=12(cos α+β2+cosα−β2)cos α+cos β=2(cos α+β2)(co sα−β2) sin αsin β=-12(cosα+β2-cosα−β2)cos α-cos β=2(sinα+β2)(sinα−β2)1+tan 2α=sec 2α 1+cot 2α=csc 2αsin 2α=2sin αcos α cos 2α=cos 2α-sin 2α=1-2sin 2α=2cos 2α-1tan (α±β)=tanα±tanβ1∓tanαtan β cot (α±β)=1∓cot αcot βcot α+cot βtanα2=1−cosαsinα=sinα1+cosα=±√1−cosα1+cosαcotα2=sinα1−cosα=1+cosαsinα=±√1+cosα1−cosα万能公式:u=tan x2(−π<x<π),则sin x=2u1+u2,cos x=1−u21+u2函数图像sec(x) csc(x) cot(x)arcsin(x) arccos(x)arctan(x) arc cot(x)[极限]函数极限x→•:(6)limx→x0f(x)=A: ∀E>0,∃δ>0,当0<|x- x0|< δ时,恒有|f(x)-A|< E.limx→x0+f(x)=A: ∀E>0,∃δ>0,当0<(x- x0)< δ时,恒有|f(x)-A|<E.limx→x0−f(x)=A: ∀E>0,∃δ>0,当0<( x0- x)< δ时,恒有|f(x)-A|< E.limx→∞f(x)=A: ∀E>0, ∃X>0,当|x|>X时,恒有|f(x)-A|<E.limx→∞+f(x)=A: ∀E>0, ∃X>0,当x>X时,恒有|f(x)-A|< E.limx→∞−f(x)=A: ∀E>0, ∃X>0,当-x>X时,恒有|f(x)-A|< E.数列极限n→∞:limn→∞f(x)=A: ∀E>0, ∃N>0,当n>N时,恒有|X n-A|< E.(1)唯一性:设limx→x0f(x)=A,limx→x0f(x)=B,则A=B.(2)局部有界性:若limx→x0f(x)存在,则存在δ>0,使f(x)在U={x|0<|x-x0|<δ内有界.(3)局部保号性:○1(脱帽)若limx→x0f(x) =A>0,则存在x0的一个去心邻域,在该邻域内恒有f(x)>0.○2(戴帽)若存在x0的一个去心邻域,在该邻域内f(x)>(≥)0,且limx→x0f(x)=A(∃),则A≥0.极限四则运算:设lim x→x 0f(x)=A(∃),lim x→x 0f(x)=B(∃),则○1lim x→x 0 [f (x )±g (x )]=A±B. ○2lim x→x 0[f (x )g (x )]=A⋅B. ○3lim x→x 0f(x)g(x)=AB(B≠0). 等价无穷小(9)sin x 1−cos x ~12x 2 arc sin x a x −1~lna ⋅xtan x (1+x )α−1~αx ~xarctan xln (1+x )e x −1lim n→∞√n n =1 , lim n→∞√a n=1, (a>0) ,lim x→0+x δ(ln x )k =0 ,lim x→+∞x k e −δx =0 (δ>0,k >0) lim n→∞√a 1n +a 2n +⋯+a m nn =max {a i }i =1,2,…,m;a i >0洛必达法则:“00”型:○1lim x→x 0f(x)=0, lim x→x 0g(x)=0; ○2f(x),g(x)在x 0的某去心领域内可导,且g’(x)≠0 ○3lim x→ x 0f′(x)g′(x)=A 或为∞.则limx→x 0f(x)g(x)=limx→x0 f′(x)g′(x)“∞∞”型:○1lim x→x 0f(x)=∞, lim x→x0g(x)=∞; ○2f(x),g(x)在x 0的某去心领域内可导,且g’(x)≠0○3lim x→x 0 f′(x)g′(x)=A 或为∞.则limx→x 0f(x)g(x)=limx→x 0 f′(x)g′(x)[注]洛必达法则能不能用,用了再说.数列极限存在准则: 1. 单调有界数列必收敛2.夹逼准则:如果函数f(x),g(x)及h(x)满足下列条件: (1) g(x)≤f(x)≤h(x); (2)limg(x)=A,limh(x)=A, 则limf(x)存在,且limf(x)=A .两种典型放缩:○1max{u i }≤∑u i n i=1≤n∙max{u i }; ○2n∙min{u i }≤∑u i n i=1≤n∙max{u i }选取的依据是谁在和式中去决定性作用海涅定理(归结原则):设f(x)在 (x 0,δ)内有定义,则lim x→x 0f(x)=A 存在⟺对任何以x 0为极限的数列{x n }(x n ≠x 0),极限lim n→∞f(x n )=A存在.连续的两种定义:(1) lim Δx→0Δy =lim Δx→0[f (x 0+Δx )−f (x 0)]=0(2) lim x→x 0f (x )=f (x 0)间断点:第一类:可去、跳跃;第二类:无穷、振荡[一元微分学]导数定义式:f’ (x 0)=dydx |x=x0=limΔx→0f (x 0+Δx )−f(x 0)Δx=limx→x 0f (x )−f(x0)x−x 0微分定义式:若Δy=A Δx +o(Δx ),则dy=A Δx . 可导的判别:(1) 必要条件:若函数f(x)在点x 0处可导,则f(x)在点x 0处连续.(2) 充要条件:f ′(x0)f +(x 0)′,f −(x 0)′都存在,且f +(x 0)′=f −(x 0)′.[注]通俗来说就是连续函数不一定可导;函数在一点可导且在该点连续,但在这点的某个邻域未必连续;函数可导,则其导函数可能连续,也可能震荡间断. 可微的判别:limΔx→0Δy−AΔx Δx=0,则f(x)可微。
(一元函数可微即可导)几个不常见的求导公式:(arccos x)’=-√2(arccot x)’=-11+x 2莱布尼茨公式:(uv )(n)= C n 0u (n)v+ C 1 n u (n-1)v’+…+C nn uv (n)常见初等函数n 阶导数:(a x )(n)=a x ⋅ln n a (1ax+b ) (n)=(−1)n a n n!(ax+b )n+1[sin (ax+b )](n)=a n sin (ax+b+nπ2) [cos (ax+b )](n)=a n cos (ax+b+nπ2)[ln (ax+b )] (n)=(−1)n−1a n (n−1)!(ax+b )n(n≥1)构造辅助函数:要证f′(x)+φ′(x)⋅f(x)=0,只要构造F(x)=f(x)⋅ⅇφ(x),证明F′(x)=0.最值定理:如果函数f(x)在闭区间[a,b]上连续,则m≤f(x)≤M,其中m,M分别为f(x)在[a,b]上的最小值和最大值.介值定理:如果函数f(x)在闭区间[a,b]上连续,m,M是f(x)在该区间上的最小值和最大值,则对任意的μ∈[m,M],∃ξ∈(a,b),使得f(ξ)=μ.零点定理:如果函数f(x)在闭区间[a,b]上连续,且满足f(a)⋅f(b)<0,∃ξ∈(a,b),使得f(ξ)=0.费马引理:设f(x)满足在x0点处{(1)可导(2)取极值则f′(x0)=0.罗尔:设f(x)满足{(1)[a,b]上连续(2)(a,b)内可导(3)f(a)=f(b)则∃ξ∈(a,b),使得f′(ξ)=0拉格朗日中值:设f(x)满足{(1)[a,b]上连续(2)(a,b)内可导则∃ξ∈(a,b),使得f(b)-f(a)=f′(ξ)(b-a),或者写成f′(ξ)=f(b)−f(a)b−a柯西中值:设f(x),g(x)满足{(1)[a,b ]上连续(2)(a,b )内可导(3)g ′(x )≠0.则∃ξ∈(a,b ),使得f (b )−f (a )g (b )−g(a)=f ′(ξ)g ′(ξ).泰勒公式:(1)带拉格朗日余项的n 阶泰勒公式设f(x)在点x 0的某个领域内n+1阶导数存在,则对该邻域内的任意点x 均有f(x)=f(x 0)+f ′(x 0)(x −x 0)+…+1n!f (n )(x 0)(x −x 0)n +f n+1(ξ)(n+1)!(x −x 0)n+1,其中ξ介于x , x 0之间,(2)带佩亚诺余项的n 阶泰勒公式设f(x)在点x 0处n 阶可导,则存在x 0的一个邻域,对于该邻域中的任一点,f(x)=f(x 0)+f ′(x 0)(x −x 0)+…+1n!f (n )(x 0)(x −x 0)n +ο((x −x 0)n ).麦克劳林:(9)e x =1+x+12!x 2+…+1n!+ο(x n )sinx=x −x 33!+…+(−1)n x 2n+1(2n+1)!+ο(x 2n+1) arcsinx=x+x 33!…+x 2n+1(2n+1)!+ο(x 2n+1) tanx=x+x 33+215x 5+ο(x 5) arctanx=x −x 33+ο(x 3) cosx=1−x 22!+x 44!−…+(−1)n x2n(2n )!+ο(x 2n )11−x=1+x+x2+ …+x n+ο(x n)11+x=1−x+x2+ …+(−1)n x n+ο(x n)ln(1+x)=x−x22+x33−…+(−1)n x n+1n+1+ο(x n+1)(1+x)a=1+αx+α(α−1)2!x2+⋯+α(α−1)⋯(α−n+1)n!+ο(x n)函数性态单调判定:若y=f(x)在区间I上有f′(x)>0,则y=f(x)在I上严格单调增加;若y=f(x)在区间I上有f′(x)<0,则y=f(x)在I上严格单调减少。