古希腊的几何学

《几何学》《几何学》是一门千年悠久的数学科学，古希腊哲学家几何学是其发源地。

几何学以三维几何形状、大小、位置和空间结构的分析、解释以及应用为基础。

它是数学的一个重要分支，以及工程学、物理和天文学的一个重要手段。

几何学的最初发展是由古希腊哲学家先知们建立的，他们用几何来解决实际问题，比如地理，测量土地。

古希腊哲学家先知也使用几何来探寻未知的事物，比如他们定义了很多几何论断，证明空间中几何图形的性质。

此后，几何学发展历经革命，在数学方面取得了重大突破。

比如，印度数学家以及Aryabhatta，一位著名的古希腊数学家Euclid等人，将几何学发展到新的高度，使几何学更具有科学性。

四象限几何作为高中几何的核心，研究的是平面的几何图形。

学习者将学习以笛卡尔坐标系来呈现几何图形，计算几何图形的面积以及直线、圆等几何图形的性质，以及研究几何图形和其他图形之间的关系。

此外，三角学也是几何学的重要研究内容。

三角学是通过研究几何图形的三角形，来推导三角形内部各个角度、边长的关系的学科。

三角学的研究将涉及三角形内部的各种性质，比如畸变、相似等。

此外，还将研究三角形的面积以及其他几何图形与三角形之间的性质。

几何学也涉及其它形式的平面图形，比如椭圆、矩形、曲线等，以及立体图形，比如正多面体、立方体等，和少数非立体图形，比如曲面图形。

几何学也将学习各种图形的性质，比如椭圆的焦点、立体图形的体积、曲面图形的交点等。

几何学是数学中一门基本的学科，也是人们解决实际问题的重要工具。

它的发展从古希腊哲学家先知们开始，历经多个革命，形成现在的几何学。

今天，几何学在许多学科中发挥着重要作用，它已经成为数学，物理，天文和工程等学科计算和解决问题的重要手段。

几何学也是科学家们探测宇宙真理的重要工具，它可以让我们更深入的了解宇宙的结构，走向实践而得出结论。

欧氏几何、罗氏几何和黎曼几何是几何学中的三个重要分支，它们分别由欧几里德、罗伯特·罗斯和伯纳德·黎曼提出，并在不同的数学和物理领域中发挥着重要作用。

这三种几何学在概念、方法和应用上有着明显的区别，让我们一起深入了解它们。

一、欧氏几何欧氏几何是以古希腊数学家欧几里德的名字命名的几何学。

它主要研究平面几何和空间几何中的点、线、面以及它们之间的关系和性质。

在欧氏几何中，有五条公理作为基础，这些公理包括点的唯一性、直线的无限延伸性等，构成了欧氏空间的基本性质和特征。

欧氏几何是最为直观和常见的几何学，在我们日常生活和实际工作中有着广泛的应用，比如建筑设计、地理测量等领域。

二、罗氏几何相较于欧氏几何，罗氏几何是一种非欧几何，由19世纪的数学家罗伯特·罗斯提出。

罗氏几何放弃了平行公设并提出了新的平行公设，即通过一点可以作出无数平行线。

这种新的理念打破了欧氏几何中平行线的概念，引入了一种新的、非直观的几何学体系。

罗氏几何虽然在直观上难以理解，但在相对论和曲率空间的研究中有着重要的应用，尤其是在描述引力场和黑洞的时候，罗氏几何的理论和方法显得尤为重要。

三、黎曼几何黎曼几何是由19世纪德国数学家伯纳德·黎曼创立的一种曲面的微分几何学。

相较于欧氏几何和罗氏几何，黎曼几何的研究范围更广，不再局限于平面和直线，而是研究了曲面和多维空间的性质和变换。

黎曼几何的理论为爱因斯坦的广义相对论奠定了基础，也在现代物理学和工程领域有着极其重要的应用。

结语通过对欧氏几何、罗氏几何和黎曼几何的深入了解，我们可以看到这三种几何学在概念、方法和应用上的明显区别。

欧氏几何在平面和直线的理论中有着直观的优势，罗氏几何在非直观的空间和曲率中有着重要的应用，而黎曼几何则进一步拓展了几何学的研究领域，为现代数学和物理学的发展提供了重要的理论基础。

在个人看来，欧氏几何、罗氏几何和黎曼几何的区别体现了数学的多样性和丰富性，也展示了数学在不同领域中的重要作用。

欧几里德几何简称“欧氏几何”。

几何学的一门分科。

公元前3世纪，古希腊数学家欧几里德把人们公认的一些几何知识作为定义和公理，在此基础上研究图形的性质，推导出一系列定理，组成演绎体系，写出《几何原本》，形成了欧氏几何。

在其公理体系中，最重要的是平行公理，由于对这一公理的不同认识，导致非欧几何的产生。

按所讨论的图形在平面上或空间中，分别称为“平面几何”与“立体几何”。

欧几里德几何指按照欧几里德的《几何原本》构造的几何学。

欧几里德几何有时就指平面上的几何，即平面几何。

三维空间的欧几里德几何通常叫做立体几何。

高维的情形请参看欧几里德空间。

数学上，欧几里德几何是平面和三维空间中常见的几何，基于点线面假设。

数学家也用这一术语表示具有相似性质的高维几何。

公理描述[编辑本段] 欧几里德几何的传统描述是一个公理系统，通过有限的公理来证明所有的“真命题”。

欧几里德几何的五条公理是：任意两个点可以通过一条直线连接。

任意线段能无限延伸成一条直线。

给定任意线段，可以以其一个端点作为圆心，该线段作为半径作一个圆。

所有直角都全等。

若两条直线都与第三条直线相交，并且在同一边的内角之和小于两个直角，则这两条直线在这一边必定相交。

第五条公理称为平行公理，可以导出下述命题：通过一个不在直线上的点，有且仅有一条不与该直线相交的直线。

平行公理并不像其他公理那么显然。

许多几何学家尝试用其他公理来证明这条公理，但都没有成功。

19世纪，通过构造非欧几里德几何，说明平行公理是不能被证明的。

（若从上述公理体系中去掉平行公理，则可以得到更一般的几何，即绝对几何。

）从另一方面讲，欧几里德几何的五条公理并不完备。

例如，该几何中的有定理：任意线段都是三角形的一部分。

他用通常的方法进行构造：以线段为半径，分别以线段的两个端点为圆心作圆，将两个圆的交点作为三角形的第三个顶点。

然而，他的公理并不保证这两个圆必定相交。

因此，许多公理系统的修订版本被提出，其中有希尔伯特公理系统。

十大数学名著数学作为一门古老而重要的学科，有许多经典的数学名著。

这些著作以其深度和广度而著称，为数学领域的发展做出了巨大贡献。

以下是十大数学名著的一些例子。

1. 《几何原本》（欧几里德）：这是古希腊数学家欧几里德创作的一本几何学经典著作。

它系统地阐述了几何学的基本原理和定理，对后世产生了深远影响。

2. 《算术》（尼科马库斯）：尼科马库斯的这本著作是古代数学的重要奠基之一。

它详细介绍了整数和有理数的运算规则，并提出了许多有关数论的问题。

3. 《元素》（欧几里德）：这本著作是欧几里德的另一部伟大之作，它系统地阐述了平面几何学、立体几何学和数论等数学领域的基本原理，并提出了一系列的定理和证明。

4. 《数论》（欧拉）：欧拉是18世纪最杰出的数学家之一，他的《数论》是现代数论的奠基之作。

这本著作涵盖了诸如质数、素数分解和同余等数论的基本概念和定理。

5. 《微积分原理》（牛顿和莱布尼茨）：牛顿和莱布尼茨同时独立地发展出微积分学，他们的这本著作系统地阐述了微积分的基本原理和方法，为现代数学和物理学的发展奠定了基础。

6. 《代数学基础》（布尔和高斯）：布尔和高斯被认为是现代代数学的奠基之一。

他们的这本著作详细介绍了代数学的基本概念和定理，包括线性代数、群论和环论等。

7. 《数学分析原理》（魏尔斯特拉斯）：魏尔斯特拉斯是19世纪最重要的数学家之一，他的这本著作系统地阐述了数学分析的基本原理和方法，包括收敛性、连续性和微分学等。

8. 《几何原理》（庞加莱）：庞加莱是20世纪最重要的数学家之一，他的这本著作在几何学领域做出了重要贡献。

它介绍了非欧几何学和拓扑学等新领域的概念和定理。

9. 《概率论》（科尔莫哥洛夫）：科尔莫哥洛夫是20世纪最重要的概率论学家之一，他的这本著作系统地阐述了概率论的基本原理和方法，对现代概率论的发展产生了重要影响。

10. 《数学之美》（吴军）：这本著作是一部介绍数学魅力的畅销书，它以通俗易懂的方式介绍了数学的各个领域和应用，帮助读者更好地理解和欣赏数学的美妙。

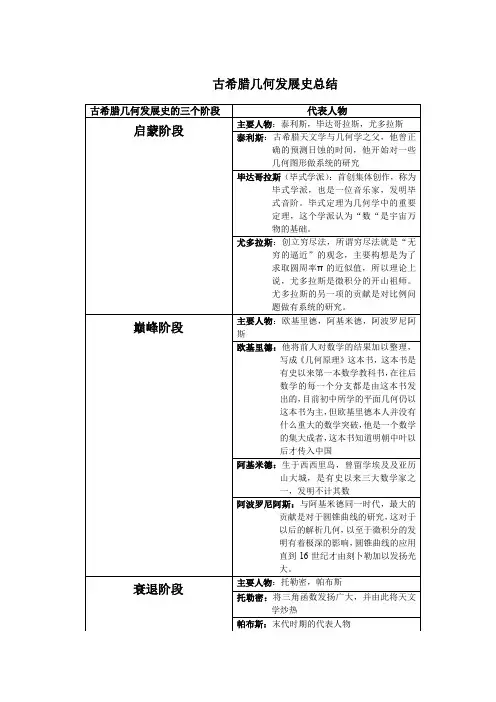
古希腊数学发展史的历程
古希腊数学发展史可以追溯到公元前6世纪至公元前4世纪的希腊城邦时期。

在这个时期，一些重要的数学思想和概念被提出并发展起来。

公元前6世纪，古希腊开始出现第一个数学家，他们被称为毕达哥拉斯学派。

毕达哥拉斯学派主要研究数和形，并强调数与万物的关系。

他们发现了一些重要的数学定理，例如毕达哥拉斯定理，该定理描述了直角三角形中直角边的关系。

公元前5世纪，古希腊的数学家泰勒斯和皮塔哥拉斯等人开始研究几何学。

泰勒斯被认为是几何学的奠基人，他提出了一些基本的几何学原理。

皮塔哥拉斯则进一步发展了几何学，并建立了一个有组织的几何学体系。

在公元前4世纪，古希腊的数学家欧几里得成为了最著名的数学家之一。

他的著作《几何原本》对几何学的发展做出了巨大贡献。

这本著作包含了很多基本几何概念和定理，被认为是古希腊几何学的经典之作。

除了几何学，古希腊数学家还研究了代数学和数论。

例如，欧几里得还研究了整数的性质，并提出了欧几里得算法来求解最大公约数。

而且，古希腊的数学家阿基米德也在代数学方面做出了重要贡献。

总的来说，古希腊数学发展史见证了许多重要数学思想和概念的诞生。

他们的贡献对后来的数学发展产生了深远影响，至今仍然被广泛应用。

古希腊人要求几何作图只许使用直尺（没有刻度，只能作直线的尺）和圆规，这种作图工具的限制使得三大几何作图问题成为数学史上的难解之题．三等分角问题即将任意一个角进行三等分．1837年，法国数学家旺策尔第一个证明了三等分角问题是古希腊那种尺规作图不可能的问题．但如果放宽作图工具的限制，该问题还是可以解决的．阿基米德创立的方法被誉为最简单的方法，他仅利用只有一点标记的直尺和圆规就巧妙地解决了这个问题．三等分角问题的深入研究导致了许多作图方法的发现及作图工具的发明．倍立方体问题即求作一个立方体，使其体积是已知一立方体的两倍，该问题起源于两千年希腊神话传说：一个说鼠疫袭击提洛岛（爱琴海上的小岛），一个预言者宣称己得到神的谕示，须将立方体的阿波罗祭坛的体积加倍，瘟疫方能停息；另一个说克里特旺米诺斯为儿子修坟，要体积加倍，但仍保持立方体的形状．这两个传说都表明倍立方体的问题起源于建筑的需要．1837年，洁国数学家旺策尔证明了倍立方体问题是古希腊那种尺规作图不可能的问题．倍立方体问题的研究促进了圆锥曲线理论的建立和发展．化圆为方问题即求作一正方形，使其面积等于一已知圆的面积．这是历史上最能引起人们强烈兴趣的问题之一，早在公元前5世纪就有许许多多的人研究它．希腊语中甚至有一个专门名词表示“献身于化圆为方问题”．1882年，德国数学家林德曼证明了化圆为方问题是古希腊那种尺规作图不可能的问题，从而解决了2000多年的悬案．如果放宽作图工具的限制，则开始有多种方法解决这个问题，其中较为巧妙的是文艺复兴时期的著名学者达·芬奇设计的：用一个底与己知圆相等，高为己知圆半径一半的圆柱在平面上滚动一周；所得矩形的面积等于已知圆面积，再将矩形化为等面积的正方形即化圆为方问题的研究促使人们开始用科学的方法计算圆周率的值，对穷竭法等科学方法的建立产生了直接影响．。

古代数学古希腊几何学的发展历程古代数学-古希腊几何学的发展历程古希腊几何学是数学的一个重要分支，对数学的发展和人类文明做出了巨大贡献。

以下是古希腊几何学发展的历程。

一、起源与早期发展古希腊几何学的起源可以追溯到公元前6世纪的古埃及。

埃及人通过测量尼罗河的洪水情况和土地的形状，逐渐积累了一些几何学的知识。

希腊人开始向古埃及人学习，并将其几何学方法和理论进一步发展完善。

公元前6世纪至公元前4世纪，古希腊的数学家们陆续提出了一些重要的基础概念和定理。

毕达哥拉斯学派的代表人物毕达哥拉斯提出了著名的毕氏定理，开创了直角三角形的研究。

此外，古希腊的数学家泰勒斯也提出了许多基础概念，例如点、线、平行等，为几何学的发展打下了基础。

二、柏拉图学派与几何学的纯粹性公元前4世纪到公元前3世纪，柏拉图学派的数学家们开始将几何学纳入到哲学的范畴中，强调几何学的纯粹性和绝对性。

柏拉图提出了一个思想实验，即“柏拉图的斯卡特殿述”，认为几何学中的图形是理念世界的具体体现。

这一观点影响了后来的许多数学家，推动了几何学的深入研究。

柏拉图学派的学生欧多克斯则进一步完善了几何学的公理化方法，提出了著名的欧几里德公理体系，为几何学的推理奠定了基础。

欧几里德的《几何原本》成为了古代几何学研究的经典著作，对后世的数学家产生了巨大的影响。

三、亚历山大几何学学派的兴起公元前3世纪至公元前1世纪，古希腊亚历山大学派成为了数学研究的中心。

该学派由亚历山大大帝的赞助人亚里士多德创建，以亚历山大城为中心进行研究。

亚历山大几何学学派的数学家们在欧几里德的基础上，进一步探索了几何学的各个方面。

该学派的代表人物阿波罗尼奥斯首次提出了椭圆、双曲线和抛物线，以及焦点和直角坐标系等概念，为后来的解析几何学的发展奠定了基础。

亚历山大几何学学派的发展使得几何学以及数学研究达到了公元前1世纪的高峰。

四、古希腊数学与现代数学的关系古希腊几何学对现代数学的发展有着深远的影响。

欧几里几何学
欧几里得几何学，也称欧氏几何学，是一种基础几何学，以古希
腊学者欧几里得的名字命名。

欧几里得几何学的研究对象是平面和空
间中的点、直线、平面、角、圆等基本图形的性质和相互关系，以及
这些图形的组合和变换。

欧几里得几何学首先在欧几里得的《几何原本》中系统呈现，后来成为数学学科中的重要分支。

欧几里得几何学建立在一系列公理之上，通过这些公理的推演证
明定理。

其中最基本的公理是“两点之间可以画一条直线”，其他公
理包括“相等的东西可以互相代替”、“相等的直角是等量的”、
“平行的直线不会相交”等。

欧几里得几何学的推导严格而逻辑性强，使其成为了理性主义哲学中的典范教材。

此外，欧几里得几何学还广
泛应用于各个领域，包括建筑、工程、物理学和艺术等。

欧几里得几何学在20世纪被发现存在一些局限性，这些局限性
主要体现在无法描述非欧几里得几何空间中的图形。

随着几何学的发展，非欧几里得几何学成为一门重要的数学学科，对几何学的发展产
生了深刻影响。

学习初中数学中的平面几何历史平面几何是数学的一个重要分支，涉及了几何图形的性质、关系及其应用等内容。

在初中数学中，学生们开始接触平面几何的基本概念和定理，帮助他们建立几何思维，培养空间想象力。

然而，了解平面几何的历史，对于学生们更好地理解和应用相关知识也非常重要。

本文将介绍平面几何的历史背景，为初中生们提供一个更全面的学习视角。

一、古希腊的几何学平面几何的历史可以追溯到古希腊的世界。

古希腊数学家毕达哥拉斯是几何学的奠基人之一。

他研究了直角三角形和勾股定理，创立了许多平面几何定律。

他的学生、继承者欧几里得则以《几何原本》而闻名，这是一本系统完整地总结了古希腊几何学知识的著作。

欧几里得在书中提出了公理化方法，明确了几何学的基本概念和定理，并以严谨的证明推导出一系列结果。

欧几里得的《几何原本》成为后世几何学的经典著作，对于几何学的发展和研究起到了重要的推动作用。

二、平面几何的发展与演进随着欧几里得几何学的建立，平面几何得到了长足的发展。

在此基础上，数学家们探索出了更多的定理和方法。

例如，阿波罗尼斯的《圆锥曲线论》中介绍了椭圆、抛物线和双曲线等曲线的平面几何性质，奠定了解析几何的基础。

斯坦纳斯提斯发现了射影几何，将平面几何的研究引向了更广阔的领域。

这些数学家的贡献使得平面几何的知识体系更加完善，为后来的学者提供了坚实的基础。

三、现代平面几何的应用随着科学技术的进步，平面几何的应用范围也越来越广泛。

在物理学中，平面几何的原理被用于描述光线的传播、反射和折射等现象。

在工程学中，平面几何的知识被应用于建筑设计、道路规划和机械制图等领域。

在计算机图形学中，平面几何的算法被用于生成三维图形的投影和渲染。

可以说，平面几何在现代社会的各个领域都发挥着重要作用。

总结起来，平面几何的历史源远流长，古希腊的几何学研究为其奠定了基础。

随着时间的推移，数学家们在这个领域中不断追求发展和创新，为我们构建了完善的理论体系。

如今，平面几何的应用已经渗透到生活的方方面面。

欧几里得几何学，又称平面几何，是一门古老而重要的数学学科，由古希腊数学家欧几里得创立。

它研究平面上的点、线和角之间的关系，通过推理和证明，发展出了一套严密的数学体系，并对后世的数学、科学和哲学产生了深远的影响。

欧几里得几何学的基本要素是点、线和角。

点是几何学最基本的概念，它没有长度、宽度和深度，只有位置。

线是由无数个点组成的，由于它没有宽度，所以可以看作是无限细小的。

角是由两条线段所夹的部分，它的大小用度数来表示。

欧几里得几何学的第一原理是平行公理，即通过一个点外一直线上存在一条与给定直线无交点的直线。

根据这一原理，欧几里得几何学发展出了许多重要定理。

例如，直线的垂直平分线将一条直线分成两个相等的部分；等边三角形的三个内角是相等的；两个平行直线被一条横截线所切割，其内角和等于两个直线夹角的和。

欧几里得几何学的核心方法是证明。

通过逻辑推理，欧几里得建立了一套完善的证明体系。

这套体系由公理、定义、命题和定理组成，其中公理是不需要证明的基本原理，定理则是通过推理和证明得出的结论。

欧几里得的《几何原本》是这套体系的最早和最完整的表述，对后世的数学研究产生了巨大的影响。

欧几里得几何学的应用广泛而深远。

它不仅在数学领域内发挥着重要的作用，也在物理学、工程学和计算机科学等领域内得到了广泛的应用。

例如，它在测量、建筑和导航等方面被广泛使用，实际上，我们身边的世界无不与几何学有着密切的关系。

然而，虽然欧几里得几何学在很长一段时间内是数学的基础，但在19世纪末，它开始受到挑战。

非欧几里得几何学的发展推翻了欧几里得的平行公理，提出了与欧几里得几何学不同的几何体系。

这一新的几何学体系证明了同一个公理集合下可以存在多个不同的真命题系统，揭示了欧几里得几何学的局限性和相对性。

综上所述，欧几里得几何学作为一门古老而重要的数学学科，研究平面上的点、线和角之间的关系。

它通过逻辑推理和严密证明，发展出了一套完善的数学体系，并对后世的数学、科学和哲学产生了深远的影响。

古希腊三大几何问题简介几何学作为数学的一个重要分支，在古希腊时期就已经引起了学者们的广泛兴趣。

在这个时期，有三个问题尤为著名，它们分别是“三平方和问题”、“倍立方问题”和“黄金分割问题”。

本文将对这三个问题进行简要介绍。

首先，我们来谈谈“三平方和问题”。

这个问题最早由古希腊数学家毕达哥拉斯开始研究。

问题的核心是，是否存在三个整数a、b、c，使得a^2+b^2=c^2成立？换句话说，是否存在一个直角三角形，其三条边的长度都是整数？这个问题被证明是可行的，即存在无数个满足条件的三个整数。

接下来，我们将讨论“倍立方问题”。

这个问题的起源可以追溯到古希腊的柏拉图学派。

问题的关键在于，是否存在一个正整数n和正整数m，使得n^3=2m^3成立？换句话说，是否存在一个立方数的两倍是另一个立方数？然而，通过数学推理和证明，这个问题被证明是不可行的，即不存在满足条件的整数解。

这一结果被称为“倍立方问题的无解性”。

最后，我们将探讨“黄金分割问题”。

这个问题源自于古希腊建筑中的黄金分割比例的运用。

黄金分割比例是指将一条线段分割为两部分，使得整条线段与较短部分的比值等于较短部分与较长部分的比值。

古希腊学者希波克拉底认为这是一种美学比例，因此引起了广泛的研究和讨论。

然而，黄金分割问题是否存在唯一解仍然是一个待解决的问题，至今仍有数学家在进行深入研究和探索。

通过本文的简要介绍，我们对古希腊三大几何问题有了一定的了解。

其中，“三平方和问题”存在无数个满足条件的三个整数解，“倍立方问题”被证明是不可行的，而“黄金分割问题”仍然是一个待解决的问题。

这些问题不仅仅是古希腊数学的瑰宝，也是后世数学研究的重要课题。

它们的探索与研究推动着数学领域的发展与进步。

简述古希腊数学的特征
古希腊数学是西方数学的重要组成部分，它的特征主要体现在以下几个方面。

一、几何学的发展。

古希腊数学的重要成就是几何学的发展。

古希腊的数学家们通过对几何学的研究，建立了一套完整的几何学理论，并发展出了一系列几何学的定理和公式，如毕达哥拉斯定理、欧几里得算法等。

二、严谨的证明方法。

古希腊数学家们非常注重证明，他们提出了一套严谨的证明方法，即公理、定义、命题和证明。

这种证明方法被后来的数学家们所继承和发展。

三、数学分析的萌芽。

古希腊数学家们在几何学的基础上，开始研究数学分析，如求极限、求导等。

虽然他们没有像后来的数学家们那样提出完整的数学分析理论，但是他们的研究为后来的数学分析奠定了基础。

四、数学的实用性。

古希腊数学家们非常注重数学的实用性，许多研究都是为了解决实际问题而进行的。

例如，他们研究了光学、力学、天文学等领域的问题，其研究成果对当时的科学和技术发展起到了重要的作用。

综上所述，古希腊数学以其严谨的证明方法、几何学的发展、数学分析的萌芽和数学的实用性等特征，为后来的数学家们提供了宝贵的理论和实践经验。

欧几里得几何学欧几里得几何学，是几何学的一个主要分支，是古希腊数学家欧几里得在公元前3世纪创立的，它主要研究平面几何和欧氏空间几何。

以下是欧几里得几何学的详细介绍：1. 起源和历史：欧几里得几何学的起源可以追溯到古希腊的数学传统。

欧几里得是最著名的几何学家之一，他在公元前3世纪的著作《几何原本》中提出了欧几里得几何学的基本原理和定理。

2. 基本原理：欧几里得几何学的基本原理包括：点、线和平面：欧几里得几何学将空间分为点、线和平面，这些基本要素是构建几何形状和证明定理的基础。

平行公设：欧几里得几何学的第五公设，也称为平行公设，规定了平行线的性质，是欧几里得几何学的重要组成部分。

共同公设：欧几里得几何学还包括共同公设，例如线段可叠加、直线可延伸等。

3. 定理和性质：欧几里得几何学包含了许多经典定理和性质，其中一些包括：勾股定理：三角形的勾股定理是欧几里得几何学中最著名的定理之一，它描述了直角三角形的边与斜边之间的关系。

射影性质：平行线的性质是欧几里得几何学的核心，它们永远不会相交，或者在无穷远处相交。

等腰三角形：等腰三角形具有两边相等的性质，以及它们的两个角相等。

圆的性质：欧几里得几何学中研究了圆的性质，包括圆的周长、面积和切线性质等。

4. 影响和应用：欧几里得几何学对数学和科学产生了深远的影响。

它奠定了几何学的基础，也为其他数学领域提供了重要的概念和方法。

欧几里得几何学的原理和定理在建筑、工程、地理学、计算机图形学等领域有广泛的应用。

5. 其他几何学：欧几里得几何学之外，还有其他几种几何学分支，如非欧几何学和投影几何学，它们研究了不满足欧几里得几何学公设的几何系统，拓展了几何学的范围。

总的来说，欧几里得几何学是数学领域的经典分支之一，它的基本原理和定理为数学研究提供了坚实的基础，并在科学和工程领域中产生了广泛的应用。

虽然它是古代的数学体系，但至今仍然具有重要的教育和研究价值。

2。

简述古希腊数学的特点古希腊数学是数学史上的一个重要时期，被认为是数学发展的黄金时代。

古希腊数学的特点主要表现在以下几个方面：1. 几何学的发展：古希腊数学主要以几何学为基础，其研究重点是图形的性质和证明。

古希腊几何学的代表人物有毕达哥拉斯、欧几里得和阿基米德等。

他们通过对几何图形的研究，建立了一套严密的几何推理体系，提出了许多重要的几何定理和概念，如毕达哥拉斯定理、欧几里得几何公理等，为后世的几何学做出了重要贡献。

2. 数学的公理化：古希腊数学倡导使用公理化的方法进行数学研究。

欧几里得的《几何原本》是古希腊数学的代表作品之一，其中详细介绍了几何学的基本概念和定理，并采用了公理化的证明方法。

古希腊数学家们认为数学应该建立在严密的逻辑基础上，通过公理和推理来证明数学结论，这种思想对数学的发展产生了深远影响。

3. 数学的抽象思维：古希腊数学家们注重数学的抽象思维能力，他们通过对具体问题的研究，发展了一套抽象的数学思维方法。

例如，毕达哥拉斯定理的发现就是基于对直角三角形的研究，但毕达哥拉斯并没有局限于具体的三角形，而是从中抽象出了一个普遍的几何定理。

这种抽象的思维方式为后来的数学发展奠定了基础。

4. 数学的形式化：古希腊数学家们注重数学的形式化表达，他们通过符号和推理规则来表示数学概念和定理，使数学思想更加清晰和精确。

例如，欧几里得几何学中使用了一系列的符号和推理规则，使得几何定理的表达更加简洁和明确。

这种形式化的表达方式为后来的数学发展提供了范例。

5. 数学的证明：古希腊数学强调证明的重要性，他们追求严密的证明过程，注重推理的逻辑性和准确性。

古希腊数学家们提出了一些著名的证明方法，如归谬法、反证法和数学归纳法等，这些方法在后来的数学研究中被广泛应用。

古希腊数学的特点可以总结为几何学的发展、数学的公理化、数学的抽象思维、数学的形式化和数学的证明。

这些特点在古希腊数学的发展过程中相辅相成，为数学的进一步发展奠定了坚实的基础。