精编制作立体几何截图和作图PPT课件

(5)连结FN、MH．则五边形FGHMN即为所求的截面．
2°截面经过的三个已知点至少有一点在多面体的面上，其余点 在棱上． 作图题5．如图，正方体ABCD―A1B1C1D1中，E、F在两条棱上， G在底面A1C1内，求过E、F、G的截面．
D1 C1
D1 C1
A1
G B1
P
A1
G M B1
F1 N
E D A B C
D1
作法：(1)连接QP、QR并延长，分 别交CB、CD的延长线于E、F. (2)连接EF交AB于Ｔ，交AD于S． (3)连接RS、TP。则多边形PQRST
C1 B1 Q
A1 R D A
P B
C
即为所求截面。
A1
D1 B1 R F A S T E D P B
C1 Q
C
作图题3．已知P、Q、R分别是四棱柱ABCD―A1B1C1D1的棱CD、 DD1和AA1上的点，且QR与AD不平行，求作过这三点的截面。
作图题6．已知直四棱柱AC1，P在面D1DCC1内，Q在面A1ADD1 内，R在棱BB1上，画出过P、Q、R三点的截面。
D1 B1 C1 P
A1
Q D A
R C
B
作法：(1)过P作PP⊥CD于点P，过Q作Q Q⊥AD于Q。 (2)在底面ABCD内连接AP、BQ，并交于H。 (3)由平行线QQ、RB作平面QQBR，连接QR。 (4)在平面QQBR内过H作KH⊥面ABCD交QR于K。 (5)由平行线PP、AA1作平面PPAA1，则K必落在面PPAA1内。 (6)在面PPAA1内，连接PK，并延长交AA1于M。 (7)在面A1ADD1内，连接MQ，并延长交DD1于S。 (8)在面D1DCC1内，连接SP，并延长交CC1于T。 (9)连接RT、RM。则多边形SMRT即为所求。
A1 Q C1 R A B D B1 P C D1
A1 Q R A M D
D1 C1 B1 P C B
I
作法：(1)连接QP并延长交DA延长线于点I。
(2)在平面ABCD内连接PI交AB于点M。 (3)连接QP、RM。则四边形PQRM即为所求。
作图题4．如图，五棱锥P―ABCDE中，三条侧棱上各有一已知 点F、G、H，求作过F、G、H的截面．
Q
E D A H B C
F
F
作法：(1)过E、F作辅助面。在面BC1内，过F作FF1∥BB1，交 B1C1于点F1，则面AFF1A1为所作的辅助面． (2)在面AFF1A1内，延长F1A1交FE的延长线于P． (3)在面A1B1C1D1内，连接PG交A1B1于M．并延长交B1C1于M。 (4)连结ME并延长与BA延长线交于Q，连接QF交AD于H． (5)连结EH，FN．则五边形EHFNM为所求的截面．
作图题8．在侧棱和高的夹角为α的正四棱锥中，求作一个过底面 顶点且与这点所对侧棱垂直的截面(α＜45°)。 S
S
E H N D a A B M G
D
C
C
A
B
作法：(1)在平面SAC中，作AE⊥SC于点E。 (2)在底面ABCD内过A作a∥BD。 (3)延长CB、CD分别交a于点M、N。 (4)连接EM、EN，分别交SB、SD于点G、H。 (5)连接AG、AH。则多边形AGEH即为所求。
D1 B1 C1 P
D1
C1 B1 P T
A1
A1 S K D Q' H
Q D A
R C
Q M A
R P' C
B
B
3°截面经过的三个已知点中，有两个点在同一棱上，第三点在多 面体内． 作图题7．试画出过正三棱柱ABC―A1B1C1的底边BC及两底中心 连线OO1中点的截面。 F
A1 O1 B1
M
D1
M
Байду номын сангаас
作法：(1)在底面AC内，过E、F作直线EF分别与DA、DC的 延长线交于L、M． (2)在侧面A1D内，连结LG交AA1于K． (3)在侧面D1C内，连结GM交CC1于H． (4)连结KE、FH．则五边形EFHFK即为所求的截面．
作图题2．P、Q、R三点分别在直四棱柱AC1的棱BB1、CC1和 DD1上，试画出过P、Q、R三点的截面．
P
P K L H E A
C
F H E A G B D
F S
N M
T
D G C B
作法：(1)将侧面PAB、PBC、PDE伸展得到三棱锥P―BST． (2)在侧面PBS内，连结并延长GF，交PS于K． (3)在侧面PBT内，连结并延长GH交PT于L．
(4)在侧面PST内，连结KL分别交PD、PE于M、N．
C1
A1
E
G
O1
D1
C1
B1
M
A O B D
C
A
O B
C D
作法：(1)过A1A和OO1作平面AOO1A1，交BC于D，交B1C1于D1， 则D、D1分别为BC、B1C1的中点。 (2)在平面A1AM内，作直线DM交上底面A1B1C1于点G。 (3)在平面A1B1C1内，过G作EF∥B1C1交A1B1于E，交A1C1于F。 (4)连接BE，CF。则多边形BCFE为所求。
4°截面经过的三个已知点两两不在同一面内的棱上． 作图题9．P、Q、R三点分别在直四棱柱AC1的棱CC1、A1D1和 AB上，试画出过P、Q、R三点的截面． D1 C
立体几何专题
(1)☆多面体的截面 多面体的截面在课本 P59─例3、P63─B─1处体现。
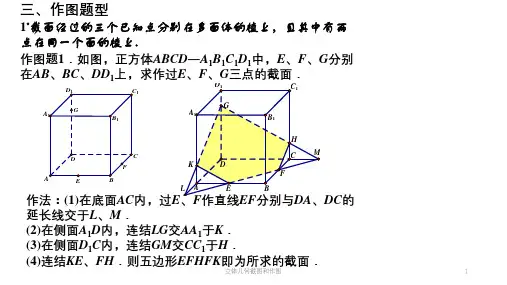
一、定义及相关要素 用一个平面去截几何体，此平面与几何体的交集，叫做这 个几何体的截面．此平面与几何体表面的交集(交线)叫做 截线．此平面与几何体的棱的交集(交点)叫做截点． 二、作多面体截面 1．方法(交线法)．该作图关键在于确定截点，有了位于多 面体同一表面上的两个截点即可连结成截线，从而求得截 面． 2．作截线与截点的主要根据有： (1)确定平面的条件． (2)如果两个不重合的平面有一个公共点，那么它们相交于 过此点的一条直线． (3)如果一条直线上的两点在一个平面内，那么这条直线上 所有的点都在这个平面内． (4)如果一条直线平行于一个平面，经过这条直线的平面与 这个平面相交，那么这条直线就和交线平行． (5)如果两个平面平行，第三个平面和它们相交，那么两条 交线平行．
三、作图题型
1°截面经过的三个已知点分别在多面体的棱上，且其中有两 点在同一个面的棱上． 作图题1．如图，正方体ABCD―A1B1C1D1中，E、F、G分别 在AB、BC、DD1上，求作过E、F、G三点的截面．
D1 G B1 C1
D1
C1
A1
A1
G B1 H
D F A E B
C
C K L A D F E B