工程材料力学性能优秀课件

格式：ppt
大小：2.78 MB
文档页数：110

下载文档原格式

材料力学材料的力学性能优质课件

结论与讨论
卸载
第3章轴向载荷作用下材料旳力学性能
结论与讨论
再加载
第3章轴向载荷作用下材料旳力学性能
结论与讨论
将卸载再加载曲线与原来旳应力-应变曲线进行比较(图中曲线OAKDE上旳虚线所示)，能够看出：K点旳应力数值远远高于A点旳应力数值，即百分比极限有所提升；而断裂时旳塑性变形却有所降低。这种现象称为应变硬化。工程上常利用应变硬化来提升某些构件在弹性范围内旳承载能力。
延伸率和截面收缩率旳数值越大，表白材料旳韧性越好。工程上一般以为δ>5％者为韧性材料； δ＜5％者为脆性材料。
第3章轴向载荷作用下材料旳力学性能
单向压缩时材料旳力学行为
返回总目录
返回
第3章轴向载荷作用下材料旳力学性能
单向压缩时材料旳力学行为
材料压缩试验，一般采用短试样。低碳钢压缩时旳应力-应变曲线。与拉伸时旳应力-应变曲线相比较，拉伸和压缩屈服前旳曲线基本重叠，即拉伸、压缩时旳弹性模量及屈服应力相同，但屈服后，因为试样愈压愈扁，应力-应变曲线不断上升，试样不会发生破坏。
试样旳变形将随之消失。
这表白这一阶段内旳变形都是
弹性变形，因而涉及线性弹性阶段
在内，统称为弹性阶段。弹性阶段旳应力最高限
第3章轴向载荷作用下材料旳力学性能
弹性力学性能
百分比极限与弹性极限
大部分韧性材料百分比极限与弹性极限极为接近，只有经过精密测量才干加以区别。
第3章轴向载荷作用下材料旳力学性能
单向压缩时材料旳力学行为
第3章轴向载荷作用下材料旳力学性能
结论与讨论
返回总目录
返回
第3章轴向载荷作用下材料旳力学性能
结论与讨论

工程材料的主要力学性能27页PPT

1
0
、
倚
南
窗
以
寄
傲
，
审
容
膝
之
易
安
。
▪
26、要使整个人生都过得舒适、愉快，这是不可能的，因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情，化为上进的力量，才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者，好之者不如乐之者。——孔子
文家。汉族，东晋浔阳柴桑人（今江西九江）。曾做过几年小官，后辞官回家，从此隐居，田园生活是陶渊明诗的主要题材，相关作品有《饮酒》、《归园田居》、《桃花源记》、《五柳先生传》、《归去来兮辞》等。
工程材料的主要力学性能
6
、
露
凝
无
游
氛
，
天
高
风
景
澈
。
7、翩翩新来燕，双双入我庐，先巢故尚在，相将还旧居。
8
、
吁
嗟
身
后
名Hale Waihona Puke ，于我若
浮
烟
。
9、陶渊明（约 365年 —427年），字元亮，（又一说名潜，字渊明）号五柳先生，私谥“靖节”，东晋末期南朝宋初期诗人、文学家、辞赋家、散
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人，倚靠在明眼的跛子肩上。——叔本华
谢谢！
27

《材料力学性能》PPT课件

反向加载，规定残余伸长应力降低的现象。
注：所有退火状态和高温回火的金属与合金都有包辛格效应。可用来研究材料加工硬化的机制。
精选ppt
19
精选ppt
20
消除包申格效应的方法：
(1) 预先进行较大的塑性变形； (2) 在第二次反向受力前先使金属材料于回复或再结晶
温度下退火，如钢在400-500℃，铜合金在250-270℃退火。
如果施加交变载荷，且最大应力低于宏观弹性极限，加载速率比较大，则也得到弹性滞后环（图b）。
如果交变载荷中最大应力超过宏观弹性极限，就会得到塑性滞后环（图 c）。
精选ppt
16
金属的循环韧性
定义：
金属材料在交变载荷（或振动）下吸收不可逆变形功的能力，也称为金属的内耗或消振性。
意义：
材料力学性能指标具体数值的高低表示材料抵抗变形和断裂能力的大小，是评定材料质量的主要依据。
精选ppt
3
第1章静载荷下材料的力学性能
1.1 应力-应变曲线
拉伸试验是工业上应用最广泛的基本力学性能试验方法之一。本章将详细讨论金属材料在单向拉伸静载荷作用下的基本力学性能指标如：屈服强度、抗拉强度、断后伸长率和断面伸长率等。
循环韧性越高，机件依靠自身的消振能力越好，所以高循环韧性对于降低机器的噪声，抑制高速机械的振动，防止共振导致疲劳断裂意义重大。
精选ppt
17
1.2.4、包申格效应（Bauschinger）
精选ppt
18
包申格效应的定义：
金属材料经过预先加载产生少量塑性变形，残余应变约1-4%，卸载后再同向加载，规定残余伸长应力（弹性极限或屈服强度）增加；
精选ppt
24

《材料力学性能01》PPT课件

Tij 2阶张量
2
32=9
Tijk 3阶张量
3
33=27
物理量示例 T 1
r
T2
Ei , Pi
T3
T11 T12 T13
sij T21 T22 T23
T31 T32 T33
dijk
Tijkl 4阶张量 4
34=81
Cijkl
应力张量（Tensor）
sxx xy xz sij = yx syy yx
三、先修课程
(1)材料力学：应力应变状态、弹性变形与本构关系、强度理论等。 (2)材料科学基础：晶体学、晶体缺陷、位错理论、变形与再结晶等。
四、教学内容及要求
材料力学性能
力学行为与物理本质
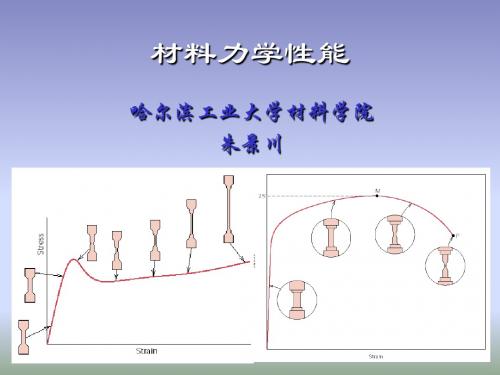
基本力学行为(简单加载)：弹性变形、塑性变形、断裂与环境相关的力学行为：疲劳、蠕变、磨损、应力腐蚀等
σp、σe的工程意义是：
因此弹簧称有称量范围的限制
对于要求服役时其应力应变关系严格遵守线性关系的机件，如测力计弹簧，是依靠弹性变形的应力正比于应变的关系显示载荷大小的，则应以比例极限作为选择材料的依据。对于服役条件不允许产生微量塑性变形的机件，设计时应按弹性极限来选择材料。
(4)屈服强度
zx zy szz
法向应力s导致材料的伸长或缩短切向应力引起材料的切向畸变
根据剪切应力互等的原理可知：xy=yx，
某点的应力状态由6个应力分量来决定
应变张量
xx ij = yx
zx
xy xz yy yx zy zz
其中xy=yx，应变也由6个独立分量决定
1773 12.2 43.0
1546 17.4 42.8
1268

材料力学性能优秀课件

号称“不沉之城”。
载有2224名乘客和船员，首航沉没于冰海，除了登上救生艇的711 人幸存外，共有1513 人葬身冰海。
绪论
2. 材料力学性能研究对象；
力学性能研究主要包括：
1）建立适当的模型和给出定量的处理方法；
2）借助微观分析，探讨材料力学性能的实质，以便能动地改造和提高材料的力学性能。
2021/3/1
材料力学性能
4
2021/3/1
材料力学性能
1)力学性能是工程结构或部件设计中最重要的数据来源。
5
Service Conditions of Turbine Blades and Vanes in a Jet Engine
Turbofan GP7000 for Airbus 380
材料力学性能
课程简介
• 专业基础核心课之一 • 与《材料力学》的区别 • 学时：54学时，学分：3学分 • 参考书：郑修麟，《材料的力学性能》
束德林，《金属力学性能》《金属力学性能》，黄明志，石德珂，金
志浩
2021/3/1
材料力学性能
2
绪论
1. 材料的力学性能在材料科学与工程中的地位；
2. 材料力学性能研究对象； 3. 材料力学性能的分类； 4. 力学性能与材料科学的发展。
2021/3/1
材料力学性能
33
பைடு நூலகம் 弹性－均匀塑性
金属及合金、部分陶瓷及非晶态高聚物。
2021/3/1
材料力学性能
34
2021/3/1
弹性－不均匀塑性
低温和高应变速率下的面心立方金属（孪生）。某些含碳原子的体心立方铁合金以及铝合金低溶质固溶体。
2021/3/1

工程材料学-材料的力学性能培训课件

1. 布氏硬度( Brinell-hardness )
布氏硬度计
用于测定硬度不高的金属材料。主要有铸铁、有色金属、低合金结构钢、结构调质钢等。
1. 布氏硬度( Brinell-hardness )
测定原理：
用一定大小的载荷P，把直径为D的淬火钢球压入被测金属的表面，保持一定的时间后卸除载荷，用金属压痕的表面积，除载荷所得的商值即为布氏硬度值。
比强度 30～37 23～36 90～111
3. 塑性指标：
塑性变形：不可恢复的永久变形。塑性是表征材料断
裂前具有塑性变形的能力。
断后伸长率δ（δ5、δ10）：
断后试样标距伸长量与原始标距之比的百分率，
即： LK L0 100%
L0
δ < 2 ~ 5% 属脆性材科
δ≈ 5 ~ 10% 属韧性材料
1.2.1 拉伸试验
3．均匀塑形变形阶段（曲线de段）
在此阶段中，试样的一部分产生塑性变形，虽然这一部分截面减小，使此处承受负荷能力下降。但由于变形强化的作用而阻止塑性变形在此处继续发展，使变形推移到试样的其它部位。这样、变形和强化交替进行，就使试样各部位产生了宏观上均匀的塑性变形。曲线上的d点是屈服阶段结束点也是加工硬化开始点。
1.2.1 拉伸试验
1．弹性变形阶段（曲线ob段）
在弹性变形阶段内的oa段，试样的伸长与外力成正比例直线关系，即每增加一定外力，就对应一定的伸长量，因此，oa段也称为线弹性变形阶段。一旦外力超过曲线上的a点时，正比例关系就破坏了。而该点对应的外力Fp称为比例变形的极限外力。ab段为弹性变形的非线性阶段，此阶段很短，一般不容易观察到。
1. 弹性指标：

工程材料力学性能1PPT课件

k：体积弹性模量，在三向压缩下，压强p与体积变化率之间的线性比例关系
18.07.2020
工程材料力学性能
30
E=2G(1+υ) E=3k(1-2 υ) 因此，各向同性材料只有两个独立分量。弹性模量的意义是以零件的刚度体现出来
18.07.2020
工程材料力学性能
6
18.07.2020
1)力学性能是工程结构或部件设计中最重要的数据来源。
工程材料力学性能
7
18.07.2020
2)力学性能通常是新材料能否由研制状态进入工程应用的基本考核指标。
工程材料力学性能
8
3）失效分析中应用。
18.07.2020
工程材料力学性能
18.07.2020
工程材料力学性能
27
f
f
a0
吸引力－－金属正离子与公有电子间库仑引力作用的结果，这是一种长程力，在比原子间距大得多的距离处它仍然起作用并占优势。
排斥力－－由同性电荷（离子，电子）间的库仑斥力以及相邻原子电子层互相重叠的泡里斥力所造成的，这是一种短程长，只有当原子距离接近时才起主导作用。
18.07.2020
工程材料力学性能
16
圆形试样
板状试样
18.07.2020
工程材料力学性能
17
试样为什么要确定比例？
标距内的绝对伸长由均匀伸长和颈缩处
的集中伸长两部分组成：
l lb lu
l lb lu
lb l0
lb l0
lu S0
lu
d0 2
l l0 S0
l
l0
d0 2
有形状和尺寸的能力。
5.
塑性－－材料在外力作用下发生不

第9章材料的力学性能ppt课件

.
交变应力下，滞弹性引起加载线和卸载线不重合，形成弹性滞后环— —加载时消耗于材料的变形功大于卸载时材料放出的变形功 —— 材料内部消耗了部分功。
28
内耗也常用自由振动的振幅衰减幅度来表征
ln An
An1
其中 An 、 An+1 分别是第n、 n+1次振动的振幅。
a
1
2
b
.
34
τP-N1 2 -G νex (-1 p 2 -ν π )a b 1 2 -G νex -2 p π bW
a：滑移面的晶面间距；b：滑移方向上的原子间
距；G：切弹性模量；：泊桑比。
W a 1-ν
称为位错宽度，表示位错导致的点阵严重畸变区的范围。W大则位错周围的原
l0和 lb：试样工作部分的初始长度和断裂后长度
不同试样长度下的不同——5、 10
断面收缩率：试样断裂后的截面积收缩率，即
S0 Sb 10% 0
S0 S0和Sb：试样的初始截面积. 和断裂后的最小截面13 积
陶瓷，脆性铸铁、铸铝，脆，断裂前有材料，一定微量的塑性变形，无颈缩
的弹性变形
多数金属塑性良好，
从软到硬有统一标度，压痕清晰使结果准确。
显微维氏硬度：小压头，小载荷，在显微镜下测量，反映材料微米级微区的硬度。
.
19
9. 2 材料的变形 (Deformation of materials)
.
20
9. 2. 1 晶体的弹性变形 (Elastic deformation of crystals)
随试验方法不同，一般硬度是金属表面抵抗局部压入变形或刻画破裂的能力。
刻划硬度——莫氏硬度——表示硬度顺序，不表示软硬程度——后面的材料可划破前面的材料

第一讲工程材料的力学性能

提高表面质量，在材料表面造成一层残余压应力。
工程材料的力学性能
三、硬度表明材料表面抗其它物体压入的能力。是局部塑变抗力指标。布氏硬度HB、洛氏硬度HR、维氏硬度 HV。 1、布氏硬度HB 测定：布氏硬度计。
原理：一定载荷F作用于淬火钢球（硬质合金圆球）压入材料表面一定时间，卸载后测出压痕直径，计算出压痕面积A，则HB=F/A，单位： kg/mm2，但一般不注出单位。国标规定：HB在450以下用HBS表示；在450以上用HBW表示。测量对象：软材料，不能测量薄试样。
工程材料的力学性能
表示：640HV、800HV。适用范围：表面硬度（硬化层）。优点：载荷小，压痕浅，但测定麻烦。四、韧性 1、冲击韧性αk 表征抗冲击载荷的能力。αk=Ak/S，单位：J/cm2 通过冲击试验测定。试样有U、V型缺口试样。冲击韧性的测试按照《夏比缺口冲击试验方法》GB/T229-1994。新标准直接用冲击功表示。标准夏比U型缺口冲击试样如图4所示。
第一讲:工程材料的力学性能
主讲：曹光明
工程材料的力学性能
一、σ-ε曲线及相应的力性指标
1、弹性强度σe 4、弹性模量E
2、屈服强度σs 5、延伸率δ
二、疲劳强度
三、硬度 1、布氏硬度HB
四、韧性 1、冲击韧性
2、洛氏硬度HR 2、断裂韧性
3、抗拉强度σb 6、断面收缩率ψ
3、维氏硬度 HV
工程材料的力学性能
实际材料中存在缺陷：夹杂物、气孔等→裂纹→在应力作用下扩展 →达到临界尺寸发生失稳扩展→断裂
裂纹扩展有三种方式，如图6所示。
K1c——在裂纹扩展的临界状态下，裂纹尖端应力场强度因子值。它表
明裂纹失稳扩展的抗力大小。K1c只与材料成分、组织结构有关。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2021/2/25
工程材料力学性能
16
复合材料分类：
按基体材料分类：聚合物基复合材料（有机非金属材料、
热固性塑料、热塑性塑料）金属基复合材料陶瓷基复合材料（无机非金属材料）
2021/2/25
工程材料力学性能
17
按增强材料分类：
纤维增强复合材料
（连续长纤维增强复合材料、结构用复合材料，可以是纤维束增强，也可以是织物增强）
工程材料力学性能
2021/2/25
工程材料力学性能
1
2021/2/25
“首相一号”公务机在上海虹桥机场亮相。 “首相一号”神奇之处在于，该飞机机舱不用金属框架、不用航空铝，而是用碳纤维复合材料从里到外一层层“织”出来的，在同等外径的条件下，这样制作的机舱比传统航空铝机舱轻２０％，强度却要提高３倍。
短纤维增强复合材料
（短纤维增强复合材料如模压复合材料（SMC）和捏塑复合材料（DMC）
颗粒增强复合材料
2021/2/25
工程材料力学性能
18
同质物质复合的复合材料
基体和纤维采用同一物质构成的复合材料，如碳-碳复合材料。
从以上可以看出，在复合材料中包含了一种或几种不连续相和一种连续相，不连续相镶嵌于连续相中。通常不连续相的强度和硬度比连续相高，称作增强组分或增强材料，而连续相称为基体。
工程材料力学性能
2
复合材料的增强概念并不是新的概念。复合材料使用的历史可以追溯到几千年以前的古老年代。古代采用粘土和稻草砌成泥墙；中世纪用不同材料层合做成的弓（以木材为芯，受拉面胶有平等的纤维，受压面胶有牛角）、剑和盔甲等。近代的胶合板和钢筋混凝土结构实际上都可以算是复合材料。
现代复合材料从上个世纪40年代使用玻璃纤维增强聚合物基体复合材料（俗称玻璃钢）算起仅有几十年的历史。这种材料刚度较低，限制了它在结构件上的应用。
复合材料力学分为微观力学和宏观力学。微观力学主要研究纤维、基体组分性能与单向板性能关系；宏观力学主要研究层合板的刚度与强度分析，温湿环境影响等。
2021/2/25
工程材料力学性能
14
第九章复合材料的一般特性、增强机理
2021/2/25
工程材料力学性能
15
第一节研究对象
复合材料是由两种或多种性质不同的组分构成的材料，然而这样的材料太多了。仅当材料各组分具有明显不同的物理性质、组分间存在明显的界面，且复合后材料的性质也明显不同于组分性质时，才能把这种材料称为复合材料。
本课程主要讨论结构材料使用的复合材料，纤维增强复合材料。
2021/2/25
工程材料力学性能
19
第二节复合材料的一般特性
纤维与基体复合后，基体提供了一个连续的介质，既保持了纤维的铺设方向，又从结构上保证了纤维的载荷传递，允许纤维承受压缩和剪切载荷，同时，基体在纤维间起着分散和传递载荷的作用，也提高了纤维沿纤维方向的承载能力。因此，复合材料的性质强烈地受组分的性质、分布和相互作用的影响。
2021/2/25
工程材料力学性能
21
密集度通常用组分的体积分数或质量分数来表示。密集度不仅是影响复合材料性能的一个重要参数，而且它是复合材料制造过程中用来改变材料性能的一个易于控制的参数。
密集度分布是材料体系匀相性的量度。决定复合材料性能实际值与平均值的差异程度。
2021/2/25
工程材料力学性能
5
战斗机中大量使用复合材料，约占结构总重量20~40%，直升机中约占40~50%。
复合材料在汽车、交通运输、工业设备和化工、石油管道方面广泛应用。
F-22 “猛禽”
2021/2/25
工程材料力学性能
6
民用方面A310-300全尺寸复合材料垂直安定面翼盒、波音767地板梁和所有损伤面使用近20吨复合材料
5%
Titanium
2021/2/25
2000年
工程材料力学性能 2020年（预测）
13
目前发展和应用仍以热固性树脂基体碳纤维复合材料为主，硼纤维成本高，加工困难，用量很少，芳纶纤维吸湿开裂，吸湿增重，影响使用。
航空、航天技术的需求推动了金属基、陶瓷基和C/C复合材料的发展。
复合材料力学性能的基本特点是各向异性、可设计性和结构特性。这些性质以及它们引起的特殊力学行为是均质的各向同性材料不具备的。因此，我们需要学习有关复合材料的理论，掌握其力学行为的基本特征及有效的试验方法。
2021/2/25
工程材料力学性能
7
俄罗斯巨型运输机安-124的部件使用了5.5吨复合材料
2021/2/25
工程材料力学性能
8
2021/2/25
工程材料力学性能
9
2021/2/25
工程材料力学性能
10
2021/2/25
采用复合材料达50% 的先进大型民机“梦
幻飞机”
B-787
工程材料力学性能
11
2021/2/25
工程材料力学性能
12
先进复合材料应用动态
u应用趋势
——复合材料成为飞机结构最为重要的基本材料
Titanium 5%
飞机机体结构材料
15% Composites
65% Aluminium
15% Steel
65%
Composites
15%
St21/2/25
工程材料力学性能
20
复合材料性质可能是组分性质的体积分数和；或者，当不能用组分性质的简单体积分数和来估算时，以某种叠加方法表征组分的相互作用，从而预测复合材料的性质。因此在描述一个复合材料体系时，除了要了解组分材料及其性质外，还需要了解增强组分的几何条件（包括形状、尺寸和尺寸分布），增强组分的密集度及密集度分布和增强组分的方向。这些因素虽然很重要，但理论研究中对上述因素都说明很困难。
2021/2/25
工程材料力学性能
3
玻璃纤维增强环氧树脂复合材料制作的直升机旋翼系统，使直升机的机动性和加速性都得到改善，寿命几乎达到无限。
2021/2/25
工程材料力学性能
4
60年代高模量硼纤维的出现，硼/环氧复合F-111水平安定面的研制成功，开始了复合材料的高性能航空、航天结构上的应用。此后碳纤维、芳纶纤维相继问世，并很快形成了商品化产品，与此同时，适合各种使用环境要求的多种环氧树脂可供设计者选用，这不仅使复合材料成为高性能结构的理想的结构材料，而且也使复合材料成为科学技术上的一大突破。