第15章磁介质的磁化参考答案
- 格式:doc
- 大小:138.50 KB
- 文档页数:4

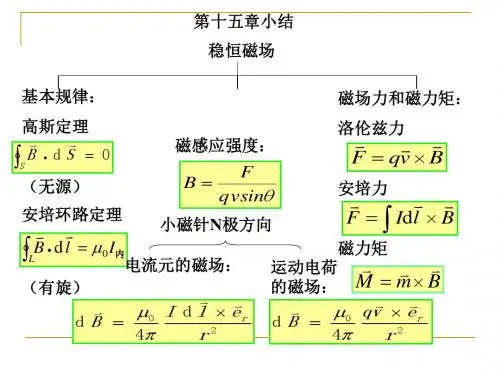

14章作业参考答案14-1.如图所示的弓形线框中通有电流I ,求圆心O 处的磁感应强度B 。
解:先求圆弧在O 点的磁感应强度:由载流圆电流在圆心处的磁场RIB 20μ=,则三分之一圆弧在圆心处的磁场RIB 601μ=,方向:垂直于纸面向外;再求直导线在O 点的磁感应强度:有限长直电流在O 处的磁感应强度为RIR IB πμπμ23)150cos 30(cos 60cos 4002=︒-︒︒=(见书71页),方向:垂直于纸面向里。
∴圆心O 处的总磁感应强度:)()(3132012-=-+=πμR IB B B ,方向垂直于纸面向里。
14-3.无限长细导线弯成如图所示的形状,其中c 部分是在xoy 平面内半径为R 的半圆,试求通以电流I 时O 点的磁感应强度。
解:a 段对O 点的磁感应强度:由无限长直电流在O 处的磁感应强度为RIB πμ20=(也可用安环定理0S B d l I μ⋅=∑⎰求得),由对称性,半无限长直电流在O 处的磁感应强度为,RIB a πμ40=方向沿y 轴负向(在O 点)。
∴04a IB j Rμπ=-。
b 段的延长线过O 点,0b B =(因为Idl 和r 夹角的正弦为零)。
c 段产生的磁感应强度为:,R IR I B C 422100μμ==方向沿z 轴正向,∴04c I B k Rμ=,则:O 点的总场强:k RI j R I B O4400μπμ+-=。
14-7.如图所示,长直电缆由半径为R 1的导体圆柱和同轴的内外半径分别为R 2、R 3的导体圆筒构成,电流沿轴线方向由一导体流入,从另一导体流出,设电流强度I 都均匀地分布在横截面上。
求距轴线为r 处的磁感应强度大小(∞<<r 0)。
解:利用安培环路定理0SB d l I μ⋅=∑⎰分段讨论。
(1)如图所示,当10r R <≤时,有:210212r IB r R ππμπ⋅=∴01212I r B R μπ=;(其中I/πR 12为电流面密度) (2)当12R r R ≤≤时,有:202B r I πμ⋅=,∴022IB rμπ=; (3)当23R r R ≤≤时,有:2223022322()r R B r I I R R πππμππ-⋅=--, ∴2232032232I B R r R r R μπ--=⋅;(其中)(2223R R I -π为电流面密度) (4)当3r R >时,有:402()B r I I πμ⋅=-,∴40B =。



•••导体内任一点的磁场强度0Ir 2ttR2再由B = pH ,有导体内任一点的磁感应强度:12TT R21 jL/Ir Ir I r 2N(2) H =—I = 200A/m f (―-1);习题1515-1. 一圆柱形无限长导体,磁导率为“,半径为/?,通有沿轴线方向的均匀电流/ ,求: (1)导体内任一点的H、B和(2)导体外任一点的片、B。
解:如图,面电流密度为:i二厶。
7T R2(1)当r<R时,利用:(方•(" =》/,利用公式M =--H,有磁化强度:M °。
“()“()2TT R~ 2TT R- 2TT R-〃()(2)当r>R时,利用:J方/有:导体外任-点的磁场强度:心总,磁感应强度:15・2・螺绕环平均周长l = lOcm,环上绕有线圈N = 200|di,通有电流I = 100/H A«试求: (1)管内为空气时〃和丹的大小;(2)若管内充满相对磁导率“,=4200的磁介质,〃和H的大小。
解:(1)B = ^nl = ;/0—/ =4^xl0-7 xlOOxlO"3 =2.5X10_4T,LDH =——=200 Ajm;A)B = pH =“o“月=4兀x 10一7 x 4200x200 = 1.057\ 15-3.螺绕环内通有电流20 A,环上所绕线圈共400匝,环的平均周长为40cm ,环内磁感应强度为1.0T,计算:(1)磁场强度;(2)磁化强度;(3)磁化率;(4)磁化面电流和相对磁导率。
解:(1)磁场强度:H = —/ = —x20 = 2xl04Aim;L 0.4D 1(2) ---------------------------------------- 磁化强度:M =——H = -2xl04 = 7.76x 10sA/m;“o4^-xlO-7(3)磁化率:乙”=“,一1,而;/r=—, .•.^=-^—-1 = 39.8-1=38.8;(4)磁化面电流密度:cr =M =--H =7.76xio5 A//n ,“o则磁化面电流:i s = s L=7.76X105X0.4=3.1X1O5A,相对磁导率:/=丄=39.8【或儿=%”+1 = 38.8 + 1=39.8】“0〃解:利用介质磁场的安培环路定理:' —工I ,考虑到导线内电流密度为:7TR-可求出磁场分布。

大学物理第十五章磁介质的磁化习题解答第十五章磁介质的磁化习题解答(仅作为参考)15.1 一均匀磁化的磁介质棒,直径为25mm ,长为75mm ,其总磁矩为12000A·m 2.求棒的磁化强度M 为多少?[解答] 介质棒的面积为S = πr 2,体积为V = Sl = πr 2l ,磁矩为p m = 12000A·m 2,磁化强度为m m p p M V V∑==? 32312000(2510/2)7510π--= =3.26×108(A·m -1).15.3 一螺绕环中心周长l = 10cm ,线圈匝数N = 200匝,线圈中通有电流I = 100mA .求:(1)管内磁感应强度B 0和磁场强度H 0为多少?(2)设管内充满相对磁导率μr = 4200的铁磁质,管内的B 和H 是多少?(3)磁介质内部由传导电流产生的B 0和由磁化电流产生的B`各是多少?[解答](1)管内的磁场强度为302200100101010NI H l --??==? = 200(A·m -1).磁感应强度为B = μ0H 0 = 4π×10-7×200 = 2.5×10-4(T).(2)当管内充满铁磁质之后,磁场强度不变H = H 0 =200(A·m -1).磁感应强度为B = μH = μr μ0H= 4200×4π×10-7×200 = 1.056(T).(3)由传导电流产生的B 0为2.5×10-4T .由于B = B 0 + B`,所以磁化电流产生的磁感应强度为B` = B - B 0 ≈1.056(T).15.5 一根磁棒的矫顽力为H c = 4.0×103A·m -1,把它放在每厘米上绕5匝的线圈的长螺线管中退磁,求导线中至少需通入多大的电流?[解答]螺线管能过电流I 时,产生的磁感应强度为B = μ0nI .根据题意,螺线管产生的磁场强度至少要与磁棒的矫顽力大小相等,但方向相反,因此B = μ0H c ,所以电流强度为I = H c /n = 4.0×103/500 = 8(A).。


第15章磁介质一、物质的磁化1、磁介质中的磁场设真空中的磁感应强度为的磁场中,放进了某种磁介质,在磁场和磁介质的相互作用下,磁介质产生了附加磁场,这时磁场中任意一点处的磁感应强度2、磁导率由于磁介质产生了附加磁场磁介质中的磁场不再等于原来真空中的磁场,定义和的比值为相对磁导率:介质中的磁导率:式中为真空中的磁导率3、三种磁介质(1)顺磁质:顺磁质产生的与方向相同,且。
略大于1(2)抗磁质:抗磁质产生的与方向相反,且。
略小于1(3)铁磁质:铁磁质产生的与方向相同,且。
远大于1二、磁化强度1、磁化强度定义为单位体积中分子磁矩的矢量和即:2、磁化强度与分子面电流密度的关系:式中为磁介质外法线方向上的单位矢量。
3、磁化强度的环流即磁化强度对闭合回路的线积分等于通过回路所包围面积内的总分子电流三、磁介质中的安培环路定律1、安培环流定律在有磁介质条件下的应用即:2、磁场强度定义为:3、磁介质中的安培环路定律:4、应用磁介质中的安培环路定律的注意点:(1)的环流只与传导电流有关,与介质(或分子电流)无关。
(2)的本身()既有传导电流也与分子电流有关。
既描写了传导电流磁场的性质也描写了介质对磁场的影响。
(3)要应用磁介质中的安培环路定律来计算磁场强度时,传导电流和磁介质的分布都必须具有特殊的对称性。
5、磁介质中的几个参量间的关系:(1)磁化率(2)与的关系(3)与等之间的关系四、磁场的边界条件(界面上无传导电流)ေ、壁介蔨分界面伤边磁感应强度的法向分量连廭,即Ҩ2、磁介谨分界面两龹的磁场强嚦纄切向分量连续,即:Ƞ3 磃感应线的折射定律ā*怎义如图15-1所示)五、铁磁物贩q、磁畴:电子ꇪ旋磁矩取向相同的對区域。
2、磁化曲线(图55-2中曲线)ေ磁导率曲线(图15-2中??曲线)4、磁滞回线ေ图17耩3)图中乺矫끽嚛㠂5、铁磁质与非铁㳁质的主要区别:铁磁物质产生的附加磁场错误!未定义书签。
的比原来真空中的磁场大得多。

磁介质的磁化与磁化强度在日常生活中,我们常常会接触到一些与磁性有关的物品,比如磁铁、磁卡等等。
这些物品之所以具有磁性,是因为它们含有一种特殊的物质,即磁介质。
那么,磁介质的磁化与磁化强度是如何产生的呢?首先,我们来了解一下什么是磁介质。
磁介质是指能够被磁场影响而发生磁化的物质,它可以是固体、液体或气体。
在磁介质中,存在着微观的磁性基本元件,如铁磁颗粒或分子磁矩。
当外加磁场作用于磁介质时,这些基本元件会发生重新排列,从而产生宏观上的磁化效应。
磁介质的磁化过程可以分为自发磁化和感应磁化两种方式。
自发磁化是指在没有外加磁场作用时,磁介质自身就具有磁化强度。
这一现象主要存在于铁磁体中,比如铁、镍和钴等物质。
在自发磁化过程中,铁磁体中的微观磁矩会自发地同向排列,并形成磁畴结构。
这种自发磁化的状态使得铁磁体对外加磁场有较强的响应能力,也使得它具有较高的磁导率和磁化强度。
而感应磁化则是指在外加磁场的作用下,磁介质发生磁化的过程。
在感应磁化的过程中,外加磁场会引起磁介质中微观磁矩的重新排列,从而使整个磁介质产生磁化效应。
感应磁化主要存在于顺磁体和抗磁体中。
顺磁体是指在外加磁场作用下,磁介质中的微观磁矩会沿外磁场方向排列,从而增强外磁场的磁感应强度。
相反,抗磁体是指在外加磁场作用下,磁介质中的微观磁矩会沿外磁场方向反向排列,从而减弱外磁场的磁感应强度。
磁化强度是描述磁介质磁化程度的物理量,它反映了磁介质对外磁场的响应能力。
磁化强度可以通过磁化矢量来表示,其大小与物质的磁化程度成正比。
磁化矢量的方向则与磁介质中的微观磁矩排列方向一致。
磁化强度与磁场强度之间存在着一种重要的关系,即磁化强度与磁场强度的比值等于磁介质的磁导率。
磁导率可以分为磁化导率和非磁化导率两种。
磁化导率是指磁介质发生磁化时的磁导率,而非磁化导率则是指磁介质未发生磁化时的磁导率。
一般情况下,磁化导率要远大于非磁化导率。
这是因为磁介质在磁化过程中,其微观磁矩的排列会引起磁感应强度的增大,从而增强了磁导率。
2023年九年级物理第十五章【磁现象】复习测试卷一、选择题(每题3分,共24分)1.下列设备的工作原理是电磁感应现象的是()A.扬声器B.发电机C.电动机D.电磁铁2.如图所示,在一圆环形导线的中央放置一个小磁针,通入如图所示的电流时,下列说法中正确的是() A.小磁针的N极转向纸内B.小磁针的N极转向纸外C.小磁针保持不动D.小磁针的N极在纸面内沿顺时针方向转动3.如图所示,甲、乙为条形磁体,中间是电磁铁,虚线是表示磁极间磁场分布情况的磁感线,则可以判断图中A、B、C、D四个磁极依次是()A.N、N、S、S B.S、S、N、SC.N、N、S、N D.S、S、N、N4.【2023·驻马店期末】一次家庭探究活动中,小明将一个正在发光的灯泡放到U形磁体中间,惊讶地发现灯丝在不停晃动。
关于这种现象,下列说法中正确的是()A.灯丝晃动是电磁感应现象B.灯丝晃动时是将内能转化成了机械能C.灯丝晃动是由于磁体能吸引钨这种金属D.灯丝晃动是由于磁场对电流的作用5.如图所示的自动控制电路中,当开关S断开时,工作电路的情况是()A.灯亮,电动机转起来,电铃响B.灯亮,电动机转起来,电铃不响C.灯不亮,电动机不转,电铃响D.灯亮,电动机不转,电铃不响6.【2022·广东】图中的a表示垂直于纸面的一段导线,它是闭合电路的一部分,当a在下列磁场中沿图中所示方向运动时,不会产生感应电流的是()7.【2022·营口】下列四个实验能反映动圈式话筒工作原理的是()8.图甲是磁悬浮台灯,灯泡内部装有磁体和半导体芯片,灯座内有如图乙所示电磁铁。
灯座通电后,灯泡会悬浮在灯座上方,半导体芯片发光。
下列说法正确的是()A.发光的半导体芯片电阻为零B.灯泡悬浮是利用同名磁极相互排斥的原理C.通电后电磁铁具有磁性说明磁能生电D.通电后电磁铁的下端为S极二、填空题(每空2分,共30分)9.小磁针静止时N极会自动转向地球的______(填“北”或“南”)方,因为地球本身就相当于一个巨大的磁体,它周围的磁场分布跟________相似,如图所示,是描绘某一磁体周围磁场的部分磁感线,若在b点放置一个可自由转动的小磁针,则小磁针静止时,其N极指向________(填“P”或“Q”)。
磁学中的磁矩矢量与磁介质的磁化磁学是物理学的一个分支,研究的是磁场的产生、性质和相互作用。
在磁学中,磁矩矢量和磁介质的磁化是两个重要的概念。
本文将深入探讨这两个概念的含义、特性以及它们之间的关系。
磁矩矢量是描述物体磁性的物理量。
它是一个矢量,用来表示物体在外磁场中的反应。
磁矩矢量的大小和方向决定了物体对外磁场的响应程度。
在经典物理学中,磁矩矢量可以通过电流产生磁场的原理来解释。
当电流通过一个线圈时,产生的磁场会引起线圈内部的磁矩矢量。
磁矩矢量的大小与线圈的面积和电流的乘积成正比,方向则由右手定则决定。
磁介质的磁化是指在外磁场的作用下,磁介质内部出现磁矩矢量的现象。
磁介质可以是固体、液体或气体,具有一定的磁导率。
当外磁场施加在磁介质上时,磁介质内部的磁矩矢量会发生定向,使得整个磁介质呈现出磁性。
磁介质的磁化程度可以通过磁化强度来衡量,磁化强度是单位体积内磁矩矢量的总和。
磁矩矢量和磁介质的磁化之间存在着密切的关系。
磁矩矢量可以看作是磁介质内部微观磁矩的矢量和。
当外磁场作用在磁介质上时,磁介质内部的微观磁矩会发生定向,使得整个磁介质呈现出磁性。
因此,磁介质的磁化实质上是磁矩矢量的总和。
磁矩矢量和磁介质的磁化在实际应用中有着广泛的应用。
在电磁感应中,磁矩矢量的变化会导致感应电动势的产生。
这一原理被广泛应用于发电机和变压器等电器设备中。
同时,在磁记录中,磁介质的磁化可以用来存储信息。
通过改变磁介质的磁化方向,可以实现信息的读写操作。
此外,磁矩矢量和磁介质的磁化还与材料的磁性有关。
根据材料的磁性,可以将物质分为顺磁性、抗磁性和铁磁性。
顺磁性材料在外磁场的作用下,磁矩矢量和外磁场方向一致。
抗磁性材料则与外磁场方向相反。
而铁磁性材料在外磁场的作用下,磁矩矢量会发生定向,使得整个材料呈现出明显的磁性。
这些不同的磁性材料在实际应用中具有不同的特性和用途。
总之,磁矩矢量和磁介质的磁化是磁学中重要的概念。
磁矩矢量描述了物体对外磁场的响应程度,而磁介质的磁化则是磁矩矢量的总和。
第15章 磁介质的磁化 参考答案一、选择题1(C),2(B),3(B),4(C),5(D)二、填空题(1). -8.88×10-6 ,抗 . (2). 铁磁质,顺磁质,抗磁质. (3). 2.50×10-4 A/m(4). 各磁畴的磁化方向的指向各不相同,杂乱无章.全部磁畴的磁化方向的指向都转向外磁场方向. (5). 矫顽力大,剩磁也大;例如永久磁铁. (6). 矫顽力小,容易退磁.三 计算题1. 半径为R 、通有电流I 的一圆柱形长直导线,外面是一同轴的介质长圆管,管的内外半径分别为R 1和R 2,相对磁导率为μr .求:(1) 圆管上长为l 的纵截面内的磁通量值; (2) 介质圆管外距轴r 处的磁感强度大小.解: (1) rIH π=2 r I B r π=20μμr l rI R R r d 2210⎰π=μμΦ120ln 2R R Il r ⋅π=μμ(2) rIB π=20μ ,与有无介质筒无关2. 一根无限长的圆柱形导线,外面紧包一层相对磁导率为μr 的圆管形磁介质.导线半径为R 1,磁介质的外半径为R 2,导线内均匀通过电流I .求∶(1) 磁感强度大小的分布(指导线内、介质内及介质以外空间). (2) 磁介质内、外表面的磁化面电流密度的大小.解∶(1) 由电流分布的对称,磁场分布必对称.把安培环路定理用于和导线同心的各个圆周环路.在导线中 (0<r <R 1) 22112r R I r H π⋅π=π⋅ ∴ 2112R IrH π=, 2101012R Ir H B π==μμ 在磁介质内部 (R 1<r <R 2)I r H =⋅π22,rIH π=22,r I B r π202μμ=.在磁介质外面 (r >R 2) rIH π23=, r I B π=203μ.(2) 磁化强度 ()rI r Ir IH BM rr π-=π-π=-=21220μμμ 介质内表面处的磁化电流密度 ()11211R I M i rS π-==μ介质外表面处 ()2212R Ii r S π-=μ3. 一个磁导率为μ1的无限长均匀磁介质圆柱体,半径为R 1.其中均匀地通过电流I .在它外面还有一半径为R 2的无限长同轴圆柱面,其上通有与前者方向相反的电流I ,两者之间充满磁导率为μ2的均匀磁介质.求磁感强度的大小B 对到轴的距离r 的分布.解:由安培环路定律 ∑⎰=⋅iI l H ϖϖd ,有21221122R Irr r R I H π=ππ⋅π= 0<r <R 1 H 2 = I / (2πr ) R 1<r <R 2H 3 = 0 r >R 2 ∵ B = μH ∴ 有B 的分布:()21112/R Ir B π=μ 0<r <R 1B 2 = μ2I / (2πr ) R 1<r <R 2B 3 = 0 r >R 24. 一铁环的中心线周长为0.3 m ,横截面积为1.0×10-4 m 2,在环上密绕300匝表面绝缘的导线,当导线通有电流3.2×10-2 A 时,通过环的横截面的磁通量为2.0×10-6 Wb .求: (1) 铁环内部的磁感强度; (2) 铁环内部的磁场强度; (3) 铁的磁化率; (4) 铁环的磁化强度.解:(1) 2102-⨯==SB ΦT(2) n = 1000 m -1, H = nI 0=32 A/m(3) 相对磁导率 4970==HBr μμ ∴ 磁化率 χm = μr 1 = 496(4) 磁化强度 M = χm H =1.59×104 A/m四 研讨题1. 顺磁质和铁磁质的磁导率明显地依赖于温度,而抗磁质的磁导率则几乎与温度无关,为什么?R 2 μ2 I O Oμ2μ1 R 2 R 1 俯视图参考解答:顺磁质的磁性主要来源于分子的固有磁矩沿外磁场方向的取向排列。
第15章 磁介质的磁化 参考答案
一、选择题
1(C),2(B),3(B),4(C),5(D)
二、填空题
(1). -8.88×10-6 ,抗 . (2). 铁磁质,顺磁质,抗磁质. (3). 2.50×10-4 A/m
(4). 各磁畴的磁化方向的指向各不相同,杂乱无章.
全部磁畴的磁化方向的指向都转向外磁场方向. (5). 矫顽力大,剩磁也大;例如永久磁铁. (6). 矫顽力小,容易退磁.
三 计算题
1. 半径为R 、通有电流I 的一圆柱形长直导线,外面是一同轴的介质长圆管,管的内外半径分别为R 1和R 2,相对磁导率为μr .求:
(1) 圆管上长为l 的纵截面内的磁通量值; (2) 介质圆管外距轴r 处的磁感强度大小.
解: (1) r
I
H π=
2 r I B r π=20μμ
r l r
I R R r d 2210⎰π=μμΦ120ln 2R R Il r ⋅π=μμ
(2) r
I
B π=20μ ,与有无介质筒无关
2. 一根无限长的圆柱形导线,外面紧包一层相对磁导率为μr 的圆管形磁介质.导线半径为R 1,磁介质的外半径为R 2,导线内均匀通过电流I .求∶
(1) 磁感强度大小的分布(指导线内、介质内及介质以外空间). (2) 磁介质内、外表面的磁化面电流密度的大小.
解∶(1) 由电流分布的对称,磁场分布必对称.把安培环路定理用于和导线同心的各个圆周环路.在导线中 (0<r <R 1) 2
2
1
12r R I r H π⋅π=π⋅ ∴ 2112R Ir
H π=
, 2
1
01012R Ir H B π==μμ 在磁介质内部 (R 1<r <R 2)
I r H =⋅π22,r
I
H π=
22,r I B r π202μμ=.
在磁介质外面 (r >R 2) r
I
H π23=, r I B π=203μ.
(2) 磁化强度 ()r
I r I
r I
H B
M r
r π-=π-
π=
-=
21220μμμ 介质内表面处的磁化电流密度 ()1
1211R I M i r
S π-==μ
介质外表面处 ()2
212R I
i r S π-=
μ
3. 一个磁导率为μ1的无限长均匀磁介质圆柱体,半径为
R 1.其中均匀地通过电流I .在它外面还有一半径为R 2的
无限长同轴圆柱面,其上通有与前者方向相反的电流I ,
两者之间充满磁导率为μ2的均匀磁介质.求磁感强度的大小B 对到轴的距离r 的分布.
解:由安培环路定律 ∑⎰=⋅i
I l H ϖ
ϖd ,有
2
1
221122R Ir
r r R I H π=ππ⋅π= 0<r <R 1 H 2 = I / (2πr ) R 1<r <R 2
H 3 = 0 r >R 2 ∵ B = μH ∴ 有B 的分布:
()
21112/R Ir B π=μ 0<r <R 1
B 2 = μ2I / (2πr ) R 1<r <R 2
B 3 = 0 r >R 2
4. 一铁环的中心线周长为0.3 m ,横截面积为1.0×10-4 m 2,在环上密绕300匝表面绝缘的
导线,当导线通有电流3.2×10-2 A 时,通过环的横截面的磁通量为2.0×10-6 Wb .求: (1) 铁环内部的磁感强度; (2) 铁环内部的磁场强度; (3) 铁的磁化率; (4) 铁环的磁化强度.
解:(1) 2102-⨯==
S
B Φ
T
(2) n = 1000 m -1, H = nI 0=32 A/m
(3) 相对磁导率 4970==
H
B
r μμ ∴ 磁化率 χm = μr 1 = 496
(4) 磁化强度 M = χm H =1.59×104 A/m
四 研讨题
1. 顺磁质和铁磁质的磁导率明显地依赖于温度,而抗磁质的磁导率则几乎与温度无关,为什么?
R 2 μ2 I O O
μ2
μ1 R 2 R 1 俯视图
参考解答:
顺磁质的磁性主要来源于分子的固有磁矩沿外磁场方向的取向排列。
当温度升高时,由于热运动的缘故,这些固有磁矩更易趋向混乱,而不易沿外磁场方向排列,使得顺磁质的磁性因磁导率明显地依赖于温度。
铁磁质的磁性主要来源于磁畴的磁矩方向沿外磁场方向的取向排列。
当温度升高时,各磁畴的磁矩方向易趋向混乱而使铁磁质的磁性减小,因而铁磁质的磁导率会明显地依赖于温度。
当铁磁质的温度超过居里点时,其磁性还会完全消失。
至于抗磁质,它的磁性来源于抗磁质分子在外磁场中所产生的与外磁场方向相反的感生磁矩,不存在磁矩的方向排列问题,因而抗磁质的磁性和分子的热运动情况无关,这就是抗磁质的磁导率几乎与温度无关的原因。
2. 在实际问题中用安培环路定理∑⎰=⋅0d I l H L
ϖ
ϖ计算由铁磁质组成的闭合环路,在得出H
后,如何进一步求出对应的B 值呢?
参考解答:
由于铁磁质的μ r 不是一个常数,因此不能用B =μr μ0H 来进行计算,而是应当查阅手册中该铁磁材料的B -H 曲线图,找出对应于计算值H 的磁感强度B 值.
3. 磁冷却。
将顺磁样品(如硝酸镁)在低温下磁化,其固有磁矩沿磁场排列时要放出能量以热量的形式向周围环境排出。
然后在绝热的情况下撤去外磁场,这样样品温度就要降低,实验中可降低到10-6K 。
试解释为什么样品绝热退磁时会降温。
参考解答:
磁冷却的原理和过程可以分几步说明如下:
(1) 把顺磁样品放入低温环境中(如温度1K 的He 气,He 气又和周围的液He 维持1K 下的热平衡)。
(2) 加外磁场(磁感强度约1T ),使顺磁样品等温磁化,顺磁质的固有磁矩在外磁场的作用下会排列起来。
在此过程中,外界对磁场做功,顺磁质的内能增加;同时样品放出热量,被周围的He 气吸收,整个系统仍维持1K 的温度不变。
(3) 迅速抽出样品周围的He 气,使样品处于绝热隔离状态。
(4) 去掉外磁场,顺磁质的磁场又趋于混乱。
此过程中,样品对外做功,内能减少,样品温度下降。
一般情况下,样品的温度可以将到10-6K 。
4. 高压容器在工业和民用领域都有着非常广泛的应用,如锅炉、储气罐、家用煤气坛等。
由于高压容器长期的使用、运行,局部区域受到腐蚀、磨损或机械损害,从而会形成潜在的威胁. 因此世界各国对于高压容器的运行都制定了严格的在役无损检测标准,以确保高压容器的安全运行。
请根据所学的知识,探索一种利用铁磁材料实现无损探伤的方法。
参考解答:
目前无损检测一般采用的方法有磁粉探伤、超声波探伤和X 射线探伤等方法。
磁粉探伤依据的是介质表面磁场分布的不连续性,可采用磁粉显示;超声波和X 射线探伤利用了波动在介质分界面反射的现象. 这些方法有的仪器结构复杂、操作繁琐,有的数据处理麻烦、价格较高,对于家用容器的检测就更为不方便.
根据LC 振荡电路的磁回路特性,一旦介质内部出现裂纹,将会引起磁导率的突变,从而使回路的电磁参数发生变化.将这一结果用于铁磁
材料表面和内部伤痕、裂纹的检测中,其检测方法原理简单,操作方便,检测灵敏度高。
LC 磁回路测量原理:
磁回路的基本模型如图所示。
A 是带线圈的磁芯, M 是待检测的材料,如容器壁。
磁回路最基本的规律是安培环路定理:
∑⎰=⋅i L I l H ϖ
ϖd . 假定整个回路采用高导磁率材料组成,而且回路中绕有N 匝线圈,线圈中电流为I ,若同一种材料中的磁场强度相同,则环路定理就可以写成:
∑∑==i
i i i i l
B l H NI μμ0
式中H i 总是沿l i 方向。
当回路中第i 段的截面积为S i 时, B i S i =φi ,由于环路内各处截面的磁通都相同, φi =φ.于是有:
.000∑∑∑∑====i i i
i i i i i i i i i S l S l l B l H NI μμφμμφμμ
上式中令:,m NI ε= ∑
=m i
i i
R S l μμ0 分别为磁回路的磁动势和磁阻,
则 )1(----=
m
m
R εφ
另一方面,根据磁回路中的自感电动势定义:
t
N t I L d d d d φε-
=-=,由式(1)得到:.d d d d 22
m m R N I R I N I N L ===φ 假定由该回路与电容C 组成LC 振荡电路, 电路的振荡频率f 为:
)2(2121----==
N
C R LC f m ππ 由式(2)可见, 在回路几何参数一定的情况下, 振荡频率由回路中的磁导率决定. 在磁回路图中,假定由容器壁M 与带线圈的磁芯A 组成回路,若维持几何参数不变,只要容器壁是均匀的,那么不同地方的回路振荡频率便相同. 在材料内部一旦出现气泡、裂纹, 则在其边界部位磁导率出现较大变化, 振荡频率就会出现跳变. 据此就可以探测到材料表面和内部的伤痕、裂纹.。