数学期望与方差
- 格式:ppt
- 大小:1.39 MB
- 文档页数:58





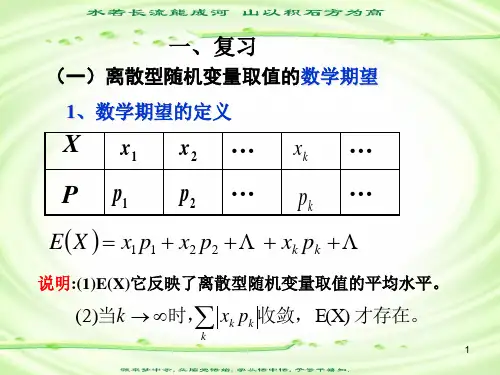



数学期望和方差的存在性问题1. 随机变量的数学期望未必都存在在数学期望的定义中,要求级数绝对收敛或积分绝对可积,我们知道,绝对收敛的级数一定收敛,绝对可积的函数一定可积。
反之都不真,故有数学期望不存在的随机变量存在。
(1) 离散的例子设随机变量X 取值 ,2,1,2)1(1=-=-k k x kk k ,相应的概率为,2,1,21==k p k k 由于∞==∑∑∞=∞=111||k k k k k p x ,所以X 的数学期望不存在 然而2ln 41312111)1(111=+-+-=-=∑∑∞=-∞= k p x k k k k k 若把上式左边级数中的各项进行重排,会收敛到不同的数 例如:2ln 2341715121311=+-++-+2ln 2181613141211=+--+-- 一个随机变量的数学期望只能是一个数,因此数学期望定义中要求的绝对收敛是必要的,它们可以保证k x 顺序的变化不影响数学期望中级数的收敛性(2) 连续的例子,见教材P .141 例5 柯西(Cauchy )分布2. 随机变量的方差未必都存在按定义 2))(()(X E X E X D -=,由于方差被定义为一种特殊形式(即随机变量X 的函数)的数学期望,而随机变量及随机变量函数的数学期望都未必存在,所以随机变量的方差也未必存在。
本章1中所举两例中的随机变量的方差都不存在.3. 数学期望存在但方差不存在参数为n 的t 分布的密度函数是 +∞<<-∞+Γ+Γ=+-x n x n n n x f n n ,)1()2()21()(212π设随机变量)2(~t X ,则其密度函数 2322)21(42)(-+=x x f ⎰+∞∞-==0)()(2dx x xf X E2X 的数学期望不存在,所以X 的方差不存在关于t 分布,其矩有一个特点,当r<n 时,有矩)(r X E ,但)(n X E 不存在,而且当n>2时,0)(=X E ,2)()(2-==n n X E X D ,故在n=2时,∞=)(X D .。

正态分布数学期望和方差
正态分布的期望和方差:求期望:ξ,期望:Eξ=x1p1+x2p2+……+xnpn。
方差;s²,方差公式:s²=1/n[(x1-x)²+(x2-x)²+……+(xn-x)²](x上有“-”)。
正态分布,也称“常态分布”,又名高斯分布,最早由A。
棣莫弗在求二项分布的渐近公式中得到。
C。
F。
高斯在研究测量误差时从另一个角度导出了它。
P。
S。
拉普拉斯和高斯研究了它的性质。
是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。
方差
方差是在概率论和统计方差衡量随机变量或一组数据时离散程
度的度量。
概率论中方差用来度量随机变量和其数学期望(即均值)之间的偏离程度。
统计中的方差(样本方差)是每个样本值与全体样本值的平均数之差的平方值的平均数。
在许多实际问题中,研究方差即偏离程度有着重要意义。
方差是衡量源数据和期望值相差的度量值。

概率论中的期望与方差概率论是一门研究随机现象的数学理论。
在概率论中,期望和方差是两个重要的概念。
本文将围绕这两个概念展开阐述,并探讨它们在概率论中的应用。
一、期望的定义与性质期望是对随机变量的平均值的度量,反映了随机变量的平均水平。
设随机变量X的分布律为P(X=x),则X的期望E(X)定义为∑[x·P(X=x)]。
期望具有线性性质,即对于任意常数a和b,E(aX+b)=aE(X)+b。
期望在概率论中有着广泛的应用。
在统计学中,期望被用于描述样本均值的性质。
在金融领域,期望被用于计算资产收益的预期值。
在工程学中,期望被用于评估系统的性能。
二、方差的定义与性质方差用于衡量随机变量的离散程度。
设随机变量X的分布律为P(X=x),则X的方差Var(X)定义为∑[(x-E(X))^2·P(X=x)]。
方差的算术平方根称为标准差。
方差的计算是概率论中的重要内容。
方差衡量了随机变量与其期望之间的差异程度,越大表示随机变量值的分散程度越大。
方差的应用包括金融学中的风险度量、质量控制中的异常度量等。
三、期望与方差的关系期望和方差是概率论中两个紧密相关的概念。
根据方差的定义可得,Var(X)=E[(X-E(X))^2]。
这说明方差是对随机变量离散程度的度量,同时也可以看作是随机变量与其期望之差的平方的期望。
期望和方差之间存在一定的关系。
例如,对于两个独立随机变量X和Y,有Var(X+Y)=Var(X)+Var(Y)。
这个性质被称为方差的可加性。
另外,若常数a和b分别为aX和bY的系数,则Var(aX+bY)=a^2·Var(X)+b^2·Var(Y)。
四、期望与方差的应用期望和方差在概率论中有着广泛的应用。
以期望为例,它可以用于计算随机变量的平均值,进而评估随机事件的结果。
在统计学中,期望被用于估计总体参数,如样本均值是总体均值的无偏估计。
方差的应用也是多种多样的。
在金融学中,方差被用于度量资产的风险程度。