带父节点的二叉链表字符串表达在RAPTOR中建立二叉树
- 格式:ppt
- 大小:3.21 MB
- 文档页数:41

二叉排序树的构造方法-回复标题:二叉排序树的构造方法详解正文:二叉排序树(Binary Search Tree,简称BST),又称二叉查找树或二叉搜索树,是一种特殊的二叉树数据结构。
其特殊性在于,对于任意一个节点,其左子树中的所有节点的值均小于该节点,而右子树中所有节点的值均大于该节点。
这种特性使得在二叉排序树上进行查找、插入和删除等操作具有较高的效率。
接下来,我们将详细阐述如何从无到有,一步步构建一棵二叉排序树。
# 一、理解二叉排序树的基本概念首先,每个节点包含三个基本元素:键(Key)、左子树指针(left)和右子树指针(right)。
键是节点存储的数据元素,用于比较大小;左子树指针指向键值小于当前节点的子树,右子树指针则指向键值大于当前节点的子树。
# 二、二叉排序树的构造步骤1. 初始化:创建一个空树作为根节点。
如果待插入的数据集为空,则构造完成的二叉排序树即为空树。
2. 插入节点:- 对于每一个待插入的数据元素key,我们从根节点开始遍历二叉排序树。
- 如果根节点为空,那么新插入的节点就成为新的根节点。
- 如果key小于当前节点的键值,且当前节点的左子树不为空,继续在左子树中递归执行插入操作;若左子树为空,则直接将key插入为当前节点的左孩子节点。
- 如果key大于当前节点的键值,同理,在右子树中执行上述操作。
- 这样,通过不断比较并移动至合适的子树,最终找到合适的位置插入新的节点,确保插入后二叉排序树的性质依然保持。
3. 实例演示:假设我们要构造一棵包含[30, 20, 40, 10, 50]序列的二叉排序树。
首先,30作为第一个元素插入,成为根节点;接着,20比30小,所以插入为30的左孩子;然后,40比30大,插入为30的右孩子;以此类推,直到所有元素插入完毕。
# 三、代码实现以下是一个简单的Python示例,展示了如何构造一个二叉排序树:pythonclass Node:def __init__(self, key):self.left = Noneself.right = Noneself.val = keyclass BST:def __init__(self):self.root = Nonedef insert(self, val):if not self.root:self.root = Node(val)else:self._insert(val, self.root)def _insert(self, val, node):if val < node.val:if node.left is None:node.left = Node(val)else:self._insert(val, node.left)elif val > node.val:if node.right is None:node.right = Node(val)else:self._insert(val, node.right)# 若val等于已存在节点的值,此处可根据需求决定是否允许重复键值# 构造过程bst = BST()data = [30, 20, 40, 10, 50]for item in data:bst.insert(item)总结来说,二叉排序树的构造是一个基于比较和递归的过程,按照特定规则将元素插入到正确的位置,从而形成满足排序特性的二叉树结构。

课程题目:按给定的先序序列来建立二叉树一、需求分析1、题目要求1.1 存储结构: 以二叉链表作为二叉树的存储结构1.2 二叉树的创建:以给定的先序序列来创建二叉树1.3 输出二叉树: 以中序和后序序列输出二叉树的结点2、测试数据:A B $ D G $ $ $ C E $ H $ $ F $ $($表示空格符号)二、概要设计ADT BinaryTree {数据对象D: D是具有相同特性的数据元素的集合。
数据关系: R1={ <a i-1,a i>|a i-1,a i ∈D, i=2,...,n }数据关系 R:若D为空集,则称为空树;否则:(1) 在D中存在唯一的称为根的数据元素root,(2) 当n>1时,其余结点可分为m (m>0)个互不相交的有限集T1, T2, …, Tm, 其中每一个子集本身又是一棵树,称为根root的子树。
基本操作:InitStack(SqStack &s) //初始化栈StackElemty(SqStack &s) //判断栈是否为空Push(SqStack &s,BiTree e) //将元素e进栈Pop(SqStack &s,BiTree &e) //出栈,栈顶元素返回给eCreateBiTree(BiTree &t) //用先序建立一个二叉树,空格表示空树InOrderTraverse(BiTree t,Status(* Visit)(TElemType e))//用非递归方式实现中序遍历,对每个元素调用函数visitPostorderTraverse(BiTree t) //用递归方式实现后序遍历} ADT BinaryTree三、详细设计#include <stdio.h>#include <stdlib.h>typedef int Status;typedef char TElemType;#define OK 1#define ERROR 0#define OVERFLOW -2#define STACK_INIT_SIZE 50#define STACKINCREMENT 10typedef struct BiTNode{//树二叉链表的存储结构TElemType data;struct BiTNode *lchlid,*rchlid;}BiTNode,*BiTree;typedef struct{//栈的存储结构BiTree *base;BiTree *top;int stacksize;}SqStack;Status InitStack(SqStack &s){//初始化栈s.base=(BiTree *)malloc(STACK_INIT_SIZE * sizeof(BiTree));if(!s.base) exit(OVERFLOW);s.top=s.base;s.stacksize=STACK_INIT_SIZE;return OK;}Status StackElemty(SqStack &s){//判断栈是否为空if(s.base!=s.top)return ERROR;return OK;}Status Push(SqStack &s,BiTree e){//将元素e进栈if(s.top-s.base>=s.stacksize){ //追加分配s.base=(BiTree*)realloc(s.base,(s.stacksize+STACKINCREMENT)*sizeof(BiTree)); if(!s.base) exit(OVERFLOW);s.top=s.base+s.stacksize;s.stacksize+=STACKINCREMENT;}*s.top++=e;return OK;}Status Pop(SqStack &s,BiTree &e){//出栈,栈顶元素返回给eif(s.top==s.base) return ERROR;e=*--s.top;return OK;}Status CreateBiTree(BiTree &t){//用先序建立一个二叉树,空格表示空树TElemType ch;scanf("%c",&ch);if(ch==' ') t=NULL;else{if(!(t=(BiTNode *)malloc(sizeof(BiTNode))))exit(OVERFLOW);t->data=ch; //生成根结点CreateBiTree(t->lchlid); //构造左子树CreateBiTree(t->rchlid); //构造右子树}return OK;}Status Visit(TElemType e){//访问函数printf("%c",e);return OK;}Status InOrderTraverse(BiTree t,Status(* Visit)(TElemType e)) {//用非递归方式实现中序遍历,对每个元素调用函数visit SqStack s;InitStack(s); //建立一个栈存储二叉树的结点BiTree p=t;while(p||!StackElemty(s)){if(p){//根指针进栈,遍历左子树Push(s,p);p=p->lchlid;}else{//根指针退栈,访问根结点,遍历右子树Pop(s,p);if(!Visit(p->data)) return ERROR;p=p->rchlid;}}printf("\n");return OK;}Status PostorderTraverse(BiTree t){//用递归方式实现后序遍历if(t){PostorderTraverse(t->lchlid); //遍历左子树PostorderTraverse(t->rchlid); //遍历右子树printf("%c",t->data); //访问结点}return OK;}void main(){BiTree t;printf("请输入一串字符:\n");CreateBiTree(t);printf("中序遍历结果为:\n");InOrderTraverse(t,Visit);printf("后序遍历结果为:\n");PostorderTraverse(t);printf("\n");}四、调试分析1、调用基本函数时要注意函数参数类型的变化,如此程序中Pop和Push2、运行程序时要正确输入,才能有结果3、define一个常量时,后面不用加分号4、关于后序遍历,用非递归的方式编写时出现错误,改写成递归调用了5、要注意一些细节,比如分号,引号、还有书写问题6、编程时一定要耐心,程序不可能一次编写成功,需要经过不断调试才能发现并改正错误7、时间复杂度:InitStack( ) O(1)StackElemty( ) O(1)Push( ) O(1)Pop( ) O(1)CreateBiTree( ) O(n)InOrderTraverse( ) O(n)PostorderTraverse( ) O(n)五、测试结果六、附录源程序文件名清单:stdio.h //标准输入输出函数头文件stdlib.h //标准库头文件。

设计以先序遍历的顺序建立二叉树的二叉链表存储结构的算法一、算法简介二叉树是一种重要的树形结构,它的建立方式有多种,其中一种是按照先序遍历的顺序建立二叉树。
这种方式需要将先序遍历序列和二叉树的存储结构相结合,采用二叉链表存储结构。
具体流程是按照先序遍历序列的顺序依次创建二叉树的各个节点,同时使用二叉链表结构保存每个节点的数据和指针信息。
二、算法实现算法的实现主要包括初始化二叉树、创建节点、建立二叉树等步骤,下面对这些步骤进行详细描述。
1. 初始化二叉树初始化二叉树需要创建一个根节点,同时将根节点的左右指针指向NULL,表示二叉树为空。
2. 创建节点创建节点需要通过输入元素数据来创建,同时节点的左右指针也需要初始化为NULL。
3. 建立二叉树建立二叉树是按照先序遍历序列来实现的,具体流程如下:(1)读入当前节点的元素数据,创建节点,并将其作为当前节点。
(2)判断当前节点的元素数据是否为结束符号(这里结束符号可以指定),如果是,则返回NULL。
(3)递归创建当前节点的左子树,将左子树的根节点赋值给当前节点的左指针。
(4)递归创建当前节点的右子树,将右子树的根节点赋值给当前节点的右指针。
(5)返回当前节点。
三、算法优化虽然上述算法实现简单明了,但它有一个缺点,即无法处理空节点的情况,如果输入的先序遍历序列中存在空节点,那么该算法就无法建立正确的二叉树了。
因此,可以在输入的先序遍历序列中使用一个特殊的符号(如#)表示空节点,在建立节点时,如果遇到该符号,则将该节点的指针设置为NULL即可。
四、算法总结按照先序遍历的顺序建立二叉树是一种基于二叉链表存储结构的建树方式。
它通过递归的方式构建整个二叉树,同时为了处理空节点的情况,还需要对输入的先序遍历序列进行特殊处理。
该算法的效率较高,适用于对先序遍历序列已知的情况下建立二叉树。

二叉排序树的实现总结
二叉排序树,也称二叉搜索树,是一种常见的数据结构,常用于快速查找和插入操作。
它的实现基于二叉树的特性,即每个节点最多有两个子节点,并且左子节点的值小于父节点的值,右子节点的值大于父节点的值。
在实现二叉排序树时,我们需要定义一个节点类,包含一个值属性和两个子节点属性。
通过递归操作,我们可以将新的值插入到二叉排序树中,确保树的有序性。
具体的插入操作如下:
1. 如果树为空,将新值作为树的根节点。
2. 如果新值小于当前节点的值,继续在左子树中插入。
3. 如果新值大于当前节点的值,继续在右子树中插入。
4. 重复上述步骤,直到找到一个空的位置,将新值插入为叶子节点。
通过上述插入操作,我们可以构建一个二叉排序树,可以快速地进行查找和插入操作。
对于查找操作,我们只需从根节点开始,比较目标值与当前节点的值的大小关系,根据大小关系选择左子树或右子树进行进一步查找,直到找到目标值或遇到空节点。
二叉排序树的优点是在有序性的基础上实现了高效的查找和插入操作。
但是,如果插入的值不是随机分布的,而是按照某种特定的顺序插入,可能会导致树的不平衡,使得查找和插入操作的效率下降。
为了解决这个问题,可以使用平衡二叉树的变种,如红黑树或AVL
树。
这些树在插入和删除操作时会进行自平衡,以保持树的平衡性,提高操作效率。
二叉排序树是一种简单而高效的数据结构,适用于快速查找和插入操作。
它的实现基于二叉树的特性,通过递归操作可以构建一个有序的树。
然而,为了保持树的平衡性,可以使用其他高级的平衡树结构。

试写出在链式存储结构上建立一棵二叉树的算法对于链式存储结构的二叉树,需要定义一个节点结构体来表示每个节点:```ctypedef struct node {int data;struct node *left;struct node *right;} node;```其中,data 表示节点的数据,left 和right 分别表示节点的左子节点和右子节点。
接下来,我们可以设计一个函数来创建一棵二叉树,算法步骤如下:1. 首先创建一个新节点,并让用户输入节点的数据。
2. 如果当前二叉树为空,则将新节点插入到根节点。
3. 否则,从根节点开始遍历二叉树。
4. 如果新节点的数据小于当前节点的数据,则继续遍历左子树。
5. 如果新节点的数据大于当前节点的数据,则继续遍历右子树。
6. 直到找到一个空位置,将新节点插入到该位置。
以下是一个示例代码实现:```c#include <stdio.h>#include <stdlib.h>typedef struct node {int data;struct node *left;struct node *right;} node;node *create_node(int data) {node *new_node = (node *)malloc(sizeof(node));new_node->data = data;new_node->left = NULL;new_node->right = NULL;return new_node;}node *insert_node(node *root, int data) {if (root == NULL) {return create_node(data);}else if (data < root->data) {root->left = insert_node(root->left, data);}else if (data > root->data) {root->right = insert_node(root->right, data);}return root;}void inorder_traversal(node *root) {if (root != NULL) {inorder_traversal(root->left);printf("%d ", root->data);inorder_traversal(root->right);}}int main() {node *root = NULL;int n, data;printf("Enter the number of nodes: ");scanf("%d", &n);printf("Enter the data of each node: ");for (int i = 0; i < n; i++) {scanf("%d", &data);root = insert_node(root, data);}printf("Inorder Traversal: ");inorder_traversal(root);printf("\n");return 0;}```该程序首先让用户输入二叉树的节点数量和每个节点的数据,然后调用insert_node 函数来插入节点,并最终输出中序遍历的结果。
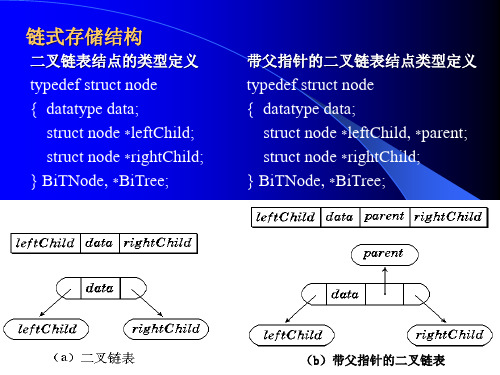
简述二叉链表的类型定义二叉链表是一种常见的数据结构,它是由节点组成的树形结构,每个节点最多有两个子节点,分别称为左子节点和右子节点。
二叉链表的类型定义包括节点结构体和二叉链表结构体两部分。
节点结构体定义节点结构体是二叉链表中最基本的数据单元,它包含三个成员变量:数据域、左子节点指针和右子节点指针。
其中,数据域用于存储节点的数据,左子节点指针和右子节点指针分别指向节点的左子节点和右子节点。
节点结构体的类型定义如下:```typedef struct BiTNode {int data; // 数据域struct BiTNode *lchild; // 左子节点指针struct BiTNode *rchild; // 右子节点指针} BiTNode, *BiTree;```在上面的代码中,BiTNode是节点结构体的别名,BiTree是指向节点结构体的指针类型。
节点结构体中的成员变量lchild和rchild都是指向节点结构体的指针类型,它们分别指向节点的左子节点和右子节点。
二叉链表结构体定义二叉链表结构体是由节点组成的树形结构,它包含一个指向根节点的指针。
二叉链表结构体的类型定义如下:```typedef struct {BiTree root; // 指向根节点的指针} BiTreeStruct;```在上面的代码中,BiTreeStruct是二叉链表结构体的别名,它包含一个指向根节点的指针root。
root指针指向节点结构体,表示二叉链表的根节点。
二叉链表的操作二叉链表是一种常见的数据结构,它支持多种操作,包括创建二叉链表、遍历二叉链表、插入节点、删除节点等。
下面我们将介绍二叉链表的常见操作。
1. 创建二叉链表创建二叉链表的过程就是构建二叉树的过程。
我们可以通过递归的方式来创建二叉链表。
具体步骤如下:1. 如果当前节点为空,则返回NULL。
2. 创建一个新节点,并将数据存储到新节点的数据域中。
第六章树和二叉树(下载后用阅读版式视图或web版式可以看清)习题一、选择题1.有一“遗传”关系:设x是y的父亲,则x可以把它的属性遗传给y。
表示该遗传关系最适合的数据结构为( )。
A.向量B.树C图 D.二叉树2.树最合适用来表示( )。
A.有序数据元素 B元素之间具有分支层次关系的数据C无序数据元素 D.元素之间无联系的数据3.树B的层号表示为la,2b,3d,3e,2c,对应于下面选择的( )。
A. la (2b (3d,3e),2c)B. a(b(D,e),c)C. a(b(d,e),c)D. a(b,d(e),c)4.高度为h的完全二叉树至少有( )个结点,至多有( )个结点。
A. 2h_lB.h C.2h-1 D. 2h5.在一棵完全二叉树中,若编号为f的结点存在右孩子,则右子结点的编号为( )。
A. 2iB. 2i-lC. 2i+lD. 2i+26.一棵二叉树的广义表表示为a(b(c),d(e(,g(h)),f)),则该二叉树的高度为( )。
A.3B.4C.5D.67.深度为5的二叉树至多有( )个结点。
A. 31B. 32C. 16D. 108.假定在一棵二叉树中,双分支结点数为15,单分支结点数为30个,则叶子结点数为( )个。
A. 15B. 16C. 17D. 479.题图6-1中,( )是完全二叉树,( )是满二叉树。
10.在题图6-2所示的二叉树中:(1)A结点是A.叶结点 B根结点但不是分支结点C根结点也是分支结点 D.分支结点但不是根结点(2)J结点是A.叶结点 B.根结点但不是分支结点C根结点也是分支结点 D.分支结点但不是根结点(3)F结点的兄弟结点是A.EB.D C.空 D.I(4)F结点的双亲结点是A.AB.BC.CD.D(5)树的深度为A.1B.2C.3D.4(6)B结点的深度为A.1B.2C.3D.4(7)A结点所在的层是A.1B.2C.3D.411.在一棵具有35个结点的完全二叉树中,该树的深度为( )。
⼆叉排序树的创建⼆叉查找树(Binary Search Tree)⼜叫⼆叉排序树(Binary Sort Tree),它是⼀种数据结构,⽀持多种动态集合操作,如 Search、Insert、Delete、Minimum 和 Maximum 等。
⼆叉查找树要么是⼀棵空树,要么是⼀棵具有如下性质的⾮空⼆叉树:1. 若左⼦树⾮空,则左⼦树上的所有结点的关键字值均⼩于根结点的关键字值。
2. 若右⼦树⾮空,则右⼦树上的所有结点的关键字值均⼤于根结点的关键字值。
3. 左、右⼦树本⾝也分别是⼀棵⼆叉查找树(⼆叉排序树)。
可以看出,⼆叉查找树是⼀个递归的数据结构,且对⼆叉查找树进⾏中序遍历,可以得到⼀个递增的有序序列。
⾸先,我们来定义⼀下 BST 的结点结构体,结点中除了 key 域,还包含域 left, right 和 parent,它们分别指向结点的左⼉⼦、右⼉⼦和⽗节点:typedef struct Node{int key;Node* left;Node* right;Node* parent;} *BSTree;⼀、BST的插⼊与构造⼆叉查找树作为⼀种动态结构,其特点是树的结构通常不是⼀次⽣成的,⽽是在查找过程中,当树中不存在结点的关键字等于给定值时再进⾏插⼊。
由于⼆叉查找树是递归定义的,插⼊结点的过程是:若原⼆叉查找树为空,则直接插⼊;否则,若关键字 k ⼩于根结点关键字,则插⼊到左⼦树中,若关键字 k ⼤于根结点关键字,则插⼊到右⼦树中。
/*** 插⼊:将关键字k插⼊到⼆叉查找树*/int BST_Insert(BSTree &T, int k){if(T == NULL){BSTree T = new BstNode;T->key = k;T->left = NULL;T->right = NULL;return 1; // 返回1表⽰成功}else if(k == T->key)return 0; // 树中存在相同关键字else if(k < T->key)return BST_Insert(T->left, k);elsereturn BST_Insert(T->right, k);} 构造⼀棵⼆叉查找树就是依次输⼊数据元素,并将它们插⼊到⼆叉排序树中的适当位置。