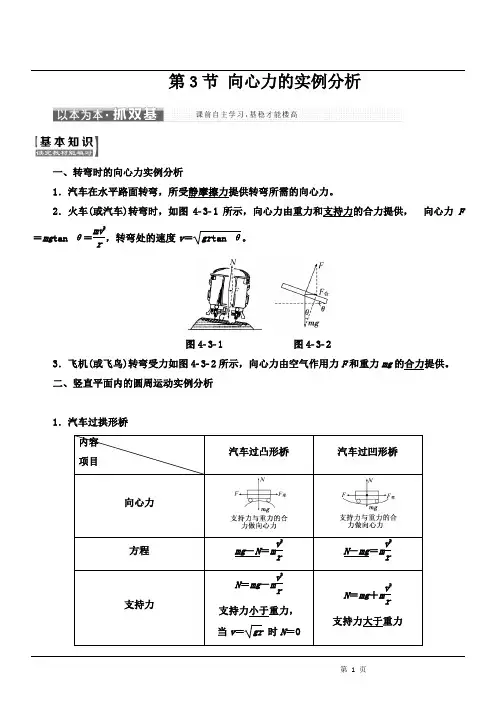
第3节 向心力的实例分析一、转弯时的向心力实例分析1．汽车在水平路面转弯，所受静摩擦力提供转弯所需的向心力。
2．火车(或汽车)转弯时，如图431所示，向心力由重力和支持力的合力提供， 向心力 F＝mg tan θ＝mv 2r，转弯处的速度v ＝gr tan θ。
图431 图4323．飞机(或飞鸟)转弯受力如图432所示，向心力由空气作用力F 和重力mg 的合力提供。
二、竖直平面内的圆周运动实例分析1．汽车过拱形桥2．过山车(在最高点和最低点)(1)向心力来源：受力如图433所示，重力和支持力的合力提供向心力。
图433(2)向心力方程在最高点：N ＋mg ＝m v 2r ，v 越小，N 越小，当N ＝0时v min ＝gr 。
在最低点：N －mg ＝m v 2r。
1．自主思考——判一判(1)火车转弯时的向心力是火车受到的合外力。
(×) (2)火车以恒定速率转弯时，合外力提供向心力。
(√) (3)做匀速圆周运动的汽车，其向心力保持不变。
(×)(4)汽车过拱形桥时，对桥面的压力一定大于汽车自身的重力。
(×)(5)汽车在水平路面上行驶时，汽车对地面的压力大小等于自身的重力大小。
(√) 2．合作探究——议一议(1)假定你是一个铁路设计的工程师，你打算用什么方法为火车转弯提供向心力？提示：要根据弯道的半径和规定的行驶速度，确定内外轨的高度差，使火车转弯时所需的向心力几乎完全由重力G 和支持力N 的合力来提供。
(2)如图434所示，滑冰运动员转弯时为什么要向转弯处的内侧倾斜身体？图434提示：倾斜身体是为了获得冰面对运动员向内侧的静摩擦力，从而获得做圆周运动所需要的向心力。
(3)过山车和乘客在轨道上的运动是圆周运动，如图435所示，过山车驶至轨道的顶部，车与乘客在轨道的下方，为什么车与乘客不会掉下来？图435提示：过山车驶至轨道的顶部时，车所受的重力和轨道的弹力的合力提供车做圆周运动的向心力，满足车做圆周运动的条件，而非近心运动或自由落体运动。
1．火车车轮的特点火车的车轮有凸出的轮缘，火车在铁轨上运行时，车轮与铁轨有水平与竖直两个接触面，这种结构特点，主要是避免火车运行时脱轨，如图436所示。
图4362．圆周平面的特点弯道处外轨高于内轨，但火车在行驶过程中，重心高度不变，即火车的重心轨迹在同一水平面内，火车的向心加速度和向心力均沿水平面指向圆心。
3．向心力的来源分析在实际的火车转弯处，外轨高于内轨，火车转弯所需的向心力完全由重力和支持力的合力提供，即mg tan θ＝m v2R，如图437所示，则v＝gR tan θ。
其中R为弯道半径，θ为轨道所在平面与水平面的夹角，v为转弯处的规定速度。
图4374．转弯时速度与轨道侧压力的关系(1)当火车行驶速度v＝gR tan θ时，重力和弹力的合力提供向心力，轮缘对内、外轨无侧压力。
(2)当火车行驶速度v＞gR tan θ时，轮缘对外轨有侧压力。
(3)当火车行驶速度v＜gR tan θ时，轮缘对内轨有侧压力。
[特别提醒] 火车做圆周运动的圆周平面是水平面，而不是斜面；火车做圆周运动的向心力沿水平方向指向圆心，而不是斜向下方。
[典例] 质量为m的火车以恒定的速率在水平面内沿一段半径为R的圆形轨道转弯，如图438所示，已知路面有一定的倾角。
当火车以速率v0在此弯道上转弯时，车轮对轨道的侧压力恰好为零。
如果火车以实际速率v(v>v0)在此弯道上转弯时，车轮将施于铁轨一个与枕木平行的压力F，试求侧压力F的大小。
图438[审题指导]第一步：抓关键点关键点获取信息车轮对轨道的侧压力恰好为零重力和支持力的合力充当向心力实际速率v>v0平行于枕木向下的弹力、重力、支持力的合力充当向心力第二步：找突破口以火车为研究对象，火车做圆周运动的平面是水平的，故合力(向心力)沿水平方向，对火车以速率v0和v在此弯道转弯时受力分析，结合牛顿第二定律列方程可求侧压力F的大小。
[解析] 用α表示路面与水平面的夹角，当火车以速率v0转弯时有mg tan α＝mv02 R①当火车以实际速率v转弯时，车轮对外轨的侧压力与外轨对车轮的侧压力是一对相互作用力，此时有N sin α＋F cos α＝mv2 R②N cos α－F sin α＝mg③联立①②③式，解得F＝v2－v02mg v04＋g2R2。
[答案] v2－v02mg v04＋g2R2火车转弯问题的解题方法(1)对火车转弯问题一定要搞清合力的方向，指向圆心方向的合外力提供物体做圆周运动的向心力，方向指向水平面内的圆心。
(2)弯道两轨在同一水平面上时，向心力由外轨对轮缘的挤压力提供。
(3)当外轨高于内轨时，向心力由火车的重力和铁轨的支持力以及内、外轨对轮缘的挤压力的合力提供，这还与火车的速度大小有关。
1．火车在拐弯时，关于向心力的分析，正确的是( )A ．由于火车本身作用而产生了向心力B ．主要是由于内外轨的高度差的作用，车身略有倾斜，车身所受重力的分力产生了向心力C ．火车在拐弯时的速率小于规定速率时，内轨将给火车侧压力，侧压力就是向心力D ．火车在拐弯时的速率大于规定速率时，外轨将给火车侧压力，侧压力作为火车拐弯时向心力的一部分解析：选D 火车正常拐弯时，重力和支持力的合力提供向心力，故A 、B 错误；当拐弯速率大于规定速率时，外轨对火车有侧压力作用；当拐弯速率小于规定速率时，内轨对火车有侧压力作用，此时，火车拐弯所需的向心力是重力、支持力和侧压力的合力来提供，故C 错误，D 正确。
2．火车在某个弯道按规定运行速度40 m/s 转弯时，内、外轨对车轮皆无侧压力。
若火车在该弯道实际运行速度为30 m/s ，则下列说法中正确的是( )A ．仅内轨对车轮有侧压力B ．仅外轨对车轮有侧压力C ．内、外轨对车轮都有侧压力D ．内、外轨对车轮均无侧压力解析：选A 火车在弯道按规定运行速度转弯时，重力和支持力的合力提供向心力，内、外轨对车轮皆无侧压力。
若火车的运行速度小于规定运行速度时，重力和支持力的合力大于火车需要的向心力，火车有做近心运动趋势，内轨对车轮产生侧压力，重力、支持力和内轨的侧压力的合力提供火车做圆周运动的向心力，故A 正确。
3．修铁路时，两轨间距是1 435 mm ，某处铁路转弯的半径是300 m ，若规定火车通过这里的速度是72 km/h 。
请你运用学过的知识计算一下，要想使内外轨均不受轮缘的挤压，内外轨的高度差应是多大？解析：火车受到的支持力和重力的合力指向轨道圆心做向心力，如图所示。
图中h 为两轨高度差，d 为两轨间距，mg tan α＝m v 2r ，tan α＝v 2gr，又由于轨道平面和水平面间的夹角一般较小，可近似认为tan α＝sin α＝hd。
因此，hd＝v2gr，又v＝72 km/h＝20 m/s，则h＝v2dgr＝202×1.4359.8×300m＝0.195 m。
答案：0.195 m1．细绳模型如图439所示，细绳系的小球或在轨道内侧运动的小球，在最高点时的临界状态为只受重力，由mg＝m v2r，得v＝gr。
图439在最高点时：(1)v＝gr时，拉力或压力为零。
(2)v>gr时，物体受向下的拉力或压力，并且随速度的增大而增大。
(3)v<gr时，物体不能达到最高点。
(实际上球未到最高点就脱离了轨道)即绳类在最高点的临界速度为v临＝gr。
2．轻杆模型如图4310所示，在细轻杆上固定的小球或在管形轨道内运动的小球，由于杆和管能对小球产生向上的支持力，所以小球能在竖直平面内做圆周运动的条件是在最高点的速度大于或等于零，小球的受力情况为：图4310(1)v＝0时，小球受向上的支持力N＝mg。
(2)0<v<gr时，小球受向上的支持力且随速度的增大而减小。
(4)v >gr 时，小球受向下的拉力或压力，并且随速度的增大而增大。
即杆类的最高点的临界速度为v 临＝0。
[特别提醒](1)细绳模型和轻杆模型在竖直平面内做圆周运动，恰能通过最高点的速度条件不同。
(2)两个模型都是根据向心力的特点确定临界条件。
[典例] 杂技演员在做“水流星”表演时，用一根细绳系着盛水的杯子，抡起绳子，让杯子在竖直平面内做圆周运动。
如图4311所示，杯内水的质量m ＝0.5 kg ，绳子总长l ＝120 cm 。
求：图4311(1)在最高点水不流出的最小速率。
(2)水在最高点速率v ＝3 m/s 时，水对杯底的压力大小。
[思路点拨] 解答本题应把握以下两点： (1)水在最高点不流出的受力条件。
(2)水和杯子做圆周运动的向心力来源。
[解析] (1)在最高点水不流出的条件是重力不大于水做圆周运动所需要的向心力，即mg ≤m v 2l2，则所求最小速率v 0＝g l2＝9.8×0.6 m/s ＝2.42 m/s 。
(2)当水在最高点的速率大于v 0时，只靠重力提供向心力已不足，此时杯子底对水有向下的力，设为N ，由牛顿第二定律有N ＋mg ＝m v 2l 2，即N ＝m v 2l2－mg ＝2.6 N由牛顿第三定律知，水对杯子的作用力N ′＝N ＝2.6 N ，方向竖直向上。
[答案] (1)2.42 m/s (2)2.6 N三步分析竖直平面内的圆周运动(1)确定圆周运动的类型：是绳模型还是杆模型。
(2)确定物体过最高点的临界条件。
(3)分析物体受力情况，根据牛顿第二定律及向心力的公式列式求解。
1.一辆满载的卡车在起伏的公路上匀速行驶，如图4312所示，由于轮胎过热，容易爆胎。
爆胎可能性最大的地段是( )图4312A．A处B．B处C．C处 D．D处解析：选D 在A、B、C、D各点均由重力与支持力的合力提供向心力，爆胎可能性最大的地段为轮胎与地面的挤压力最大处。
在A、C两点有mg－F＝m v2R，则F＝mg－mv2R<mg；在B、D两点有F－mg＝m v2R，则F＝mg＋mv2R>mg，且R越小，F越大，故F D最大，即D处最容易爆胎。
