应用数理统计第二章参数估计(3)区间估计
- 格式:ppt
- 大小:832.00 KB
- 文档页数:26


第二章 参数估计【学习目标】1、掌握矩估计的替代原则;会求已知分布中未知参数的矩估计(值)2、熟练掌握极大似然估计的思想及求法3、估计量的评价标准:无偏性、有效性、相合性的定义4、统计量的无偏性的判断;两个无偏估计的有效性判断;会用Fisher 信息量及c-R 下界进行统计量的UMVUE 充分性判断5、掌握区间估计的定义6、单个正态总体均值的区间估计(包括方差已知、方差未知);单个正态总体方差的区间估计(包括均值已知、均值未知)7、两个正态总体均值差的区间估计(方差未知);两个正态总体方差比的区间估计 8、单侧置信区间的求法 【典型例题讲解】例1、设1,,n X X 是来自均匀分布(,1)U θθ+的总体的容量为n 的样本,其中θ-∞<<+∞为未知参数,试证:θ的极大似然估计量不止一个,例如1(1)ˆXθ=,2()ˆ1n X θ=-,3(1)()11ˆ()22n XXθ=+-都是θ的极大似然估计。
解:(,1)U θθ+分布的密度函数为11()0x f x θθ≤≤+⎧=⎨⎩其他似然函数(1)()11()0n x x L θθθ≤≤≤+⎧=⎨⎩其他由于在(1)()1n x x θθ≤≤≤+上()L θ为常数,所以凡是满足:(1)()ˆˆ1n x x θθ≤≤≤+的ˆθ均为θ的极大似然估计。
从而(1)1(1)ˆX θ=满足此条件,故1(1)ˆX θ=是θ的极大似然估计;(2)由于()(1)1n X X -≤,故2()(1)()2ˆˆ11n n X X X θθ=-≤≤=+,所以2()ˆ1n Xθ=-为θ的极大似然估计;(3)由于()(1)1n X X -≤,故(1)()(1)12n X X X +-≤,(1)()()12n n X X X ++≥,从而有3(1)()(1)()(1)()31111ˆˆ()()12222n n n XXXXXXθθ=+-≤≤≤++=+,故3ˆθ也为θ的极大似然估计。


《应用数理统计》教学大纲课程名称:应用数理统计英文名称:Application of Mathematical Statistics课程编号:00907701课程学时:32课程学分:2课程性质:学位课适用专业:全校各专业预修课程:高等数学,线性代数(大学工科), 概率论与数理统计(大学工科)大纲执笔人:周大勇一、课程目的与要求本课程讨论基础数理统计的数学理论和方法,包括数理统计的基本概念,抽样分布,参数估计,假设检验,方差分析,回归分析,正交试验和质量控制初步,为众多学科专业需要较多统计工具的研究生,提供随机数学方面的训练,打下扎实的基础。
数理统计是关于数据资料的收集﹑整理﹑分析和推断的学科,通过对本课程的学习,使学生在本科工程数学的基础上,进一步较收入地掌握数理统计的基本理论和方法,培养运用数理统计的方法分析和解决有关实际问题的能力,并为今后学习后继课程打下必要的基础。
二、教学内容及学时安排第一章抽样和抽样分布 4 学时一、母体和子样二、一些常用的抽样分布第二章参数估计 8学时一、点估计和估计量的求法二、估计量的好坏标准三、区间估计第三章假设检验 8学时一、假设检验初述,二类错误二、检验母体平均数三、检验母体方差四、单侧假设检验五、分布假设检验第四章方差分析、正交试验设计 6学时一、一元方差分析二、二元方差分析三、正交试验设计第五章回归分析 6学时一、一元线性回归中的参数估计二、一元线性回归中的假设检验和预测三、可线性化的意愿非线性回归三、教材及主要参考书1、杨虎,刘琼荪,钟波《数理统计》高等教育出版社,20042、汪荣鑫《数理统计》西安交通大学出版社,19863、吴翊,李永乐,胡庆军《应用数理统计》国防科大出版社,19954、朱勇华,邰淑彩,孙韫玉《应用数理统计》武汉大学出版社,20005、茆诗松、王静龙《数理统计》华东师范大学出版社,1990。






12.4 区间估计一、 区间估计的概念参数的点估计是用θ的一个估计值),,(ˆ1n x x θ估计未知参数θ.优点: 简便、直观缺点:没有反映估计的精确度,也未给出估计值的偏差范围。
为了弥补点估计的不足,可采用另一种估计方式—-区间估计。
定义2.11. 设总体X 的分布函数为θθ),,(x F 为未知参数,),,,(21n X X X 是来自总体X 的样本。
如果存在两个统计量),,,(ˆˆ2111n X X X θθ=,),,,(ˆˆ2122n X X X θθ=,对于给定的(01)αα<<,使得αθθθ−=<<1}ˆˆ{21P (2.33) 则称区间(1ˆθ,2ˆθ)为参数θ的置信度为α−1的置信区间,1ˆθ称为置信下限,2ˆθ称为置信上限。
所谓θ的区间估计,就是要在给定α值的前提下,去寻找两个统计量1ˆθ和2ˆθ,使其满足式(2.33)。
如何寻找θ的置信区间?2下面给出寻求未知参数θ的置信区间的一般步骤: 寻求未知参数θ的置信区间的一般步骤:(1). 设法找到一个包含样本1(,,)n X X …和待估参数θ的函数12(,,,;)n U U X X X θ= ,除θ外U 不含其他未知参数,U 的分布可求出且与θ无关; (2). 对于给定的置信度α−1,由等式{}1P c U d α<<=−适当地确定两个常数c, d ;(3). 求解不等式 12(,,,;)n c U d θ<ΧΧΧ<得 1ˆθ12212ˆ(,,,)(,,,)n n θθΧΧΧ<<ΧΧΧ 从而有1ˆ{P θ12212ˆ(,,,)(,,,)}1n nθθαΧΧΧ<<ΧΧΧ=− 故(1ˆθ,2ˆθ)就是所求的置信区间。
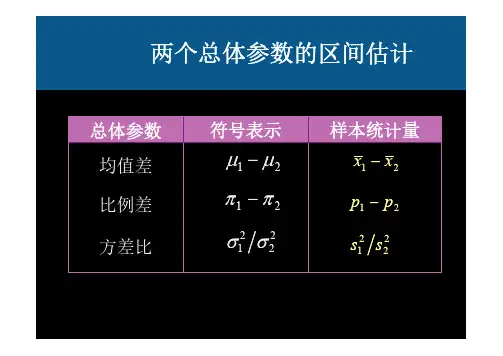
二、数学期望的置信区间1、已知DX ,求EX 的置信区间设总体X 服从正态分布N(µ,2σ),其中2σ已知。
现求总体均值µ的置信区间.设12,,,n ΧΧΧ 是来自总体X 的样本,自然用X 对µ作为点估计,因为,2(,)nN σµΧ∼故3X U =由正态分布表(附表1)可知,对于给定的α,存在一个值2u α,使得 2{||}1P U u αα<=−这里2u α是标准正态分布的α/2上侧分位数。
参数估计和区间估计是数学统计中非常重要的概念和方法,在众多统计应用领域都有广泛的应用。
通过参数估计和区间估计,我们可以利用样本数据估计总体中的未知参数,并且得到这些参数的可信区间。
参数估计是指根据样本数据对总体参数进行估计。
总体参数可以是总体均值、总体比例、总体方差等。
而样本数据是从总体中随机抽取的一部分数据。
通过计算样本数据的统计量,如样本均值、样本比例等,我们可以利用这些统计量对总体参数进行估计。
通常情况下,样本估计量与总体参数并不完全相等,而是存在一定的误差。
因此,我们需要对估计值进行修正,使得估计值更接近于总体参数的真实值。
参数估计的常用方法包括最大似然估计和矩估计等。
在参数估计的基础上,我们可以利用区间估计来研究估计值的可信程度。
区间估计是指通过样本数据对总体参数给出一个区间估计范围,这个范围称为置信区间。
置信区间是根据概率理论和统计推断方法计算出来的,它表示了一个参数的估计值在一定的置信水平下的范围。
在进行区间估计时,我们需要确定置信水平和置信区间的计算方法。
常用的置信水平有95%、99%等,这表示我们在统计推断中所采用的置信区间的正确性水平。
而置信区间的计算方法一般使用正态分布或t分布来进行。
区间估计的优势在于可以提供一个测量估计误差的范围。
在科学研究中,我们往往需要对实验结果进行合理的解释和判断。
如果我们只给出一个点估计,没有提供估计误差的范围,那么我们不能确定这个估计结果的可信程度。
而利用区间估计,我们可以提供一个置信水平下的范围,从而比较客观地评估估计结果的可信程度。
参数估计和区间估计在实际的统计应用中非常重要。
它们可以帮助我们从有限的样本数据中推断总体特征,并对推断结果给出一个可信程度的评估。
在社会科学、医学研究、市场调查等领域,参数估计与区间估计的方法被广泛应用于数据分析和决策制定中。
总的来说,数学统计中的参数估计与区间估计是我们对总体参数进行估计和评估的重要方法。
通过参数估计,我们可以利用样本数据对总体参数进行估计。
点估计量是有不足之处的,因为点估计量是一个随机变量,每给一个样本观测值点估计的值就会发生变化。
虽然这些点估计的值都在真值附近波动,但是因为真值是未知的,所以这些点估计,他与真值之间到底有多近,这是不得而知的,因此点估计不能反映估计的精度。
因此我们就想能不能给岀未知参数的一个估计范围,并使苴包含增值的可靠性,达到一泄的要求,这就是我们今天要给大家介绍的区间估计。
二、讲授新课:引例,估计一下某人的年龄范围。
第一种你可能会选择1岁到100岁,第二种区间估计,20岁到21岁。
很明显,第一种区间长,他的可信度高,也就是说,真值100%都在这个区间里而,但是精确度却很低。
第二种区间短,这时可信度就低,也就是说,真值是不是在这个区间里而呢?因为区间太短可能性就很低了,它的精确度却很髙。
因此,我们发现可信度和精确度是一对矛盾,提高了可信度,精确度就下降了,提高了精确度,可信度就会下降,那么在他们两者之间,我们应该如何取舍呢?统计学家奈曼提出了处理原则,先确左可以接受的可信度的前提下,尽屋的提髙我们的精确度。
因此,我们首先来确龙区间估计的可信度,区间估计的可信度也被称为苣信度,我们用1-Q来表示。
1-&我们经常90%, 95%, 99%等,表示这个区间可信的程度。
1、区间估计的槪念:设总体的未知参数为<9,也就是我们要估计的参数。
由样本xl到xn确泄了两个统计量,R和玄对于给定的实数a(Ovavl)满足<0<O2)>\-a我们就称随机区间(&,玄)为&置信度为1 - a的置信区间,其中1 - a又称为置信水平或置信槪率,a显著性水平。
1-a这个宜信水平反映了区间的可信度。
0.-0.这个区间长度反映了区间的精确度。
(在左义中,我们要特别注意定义式的理解&是貞. 值,它不是一个随机变呈:,而是一个数,它要么在这个区间范用里而,要么不在这个区间范用里而,那么这个1-a的概率又从何谈起呢?我们可以这样理解,比如我们令1-等于0.95,那么就相当于抽取了100次样本,其中有约95个包含真值,而另外的5个不包含真值。
应用数理统计方法一、前言数理统计是一门基础性的学科,它在各个领域中都有着广泛的应用。
本文将介绍数理统计的基本概念和方法,以及如何应用这些方法解决实际问题。
二、基本概念1.总体和样本总体是指研究对象的全体,样本是从总体中抽取出来的一部分。
在实际应用中,由于总体往往非常庞大,因此我们只能对样本进行研究,通过对样本的研究来推断总体的特征。
2.参数和统计量参数是描述总体特征的数字指标,如平均数、方差等;统计量则是描述样本特征的数字指标,如样本均值、样本方差等。
通过对统计量进行分析,我们可以推断出总体参数的值。
3.抽样方法抽样方法包括随机抽样、系统抽样、整群抽样等。
其中随机抽样是最常用的一种方法,在实际应用中也被广泛采用。
三、数据处理1.数据收集在进行数据处理之前,首先需要收集数据。
数据可以通过问卷调查、实验观测等方式获取。
2.数据清洗在收集到数据之后,需要对数据进行清洗。
数据清洗包括删除重复数据、填补缺失数据等,以保证数据的准确性和完整性。
3.描述统计描述统计是对收集到的数据进行总结和分析的过程。
常用的描述统计方法包括频数分布、直方图、箱线图等。
四、概率分布1.离散型随机变量离散型随机变量是指取有限或无限个值的随机变量,如二项分布、泊松分布等。
2.连续型随机变量连续型随机变量是指取任意实数值的随机变量,如正态分布、指数分布等。
五、参数估计在实际应用中,我们往往只能通过样本来推断总体参数的值。
参数估计是根据样本统计量来推断总体参数值的过程。
常用的参数估计方法包括点估计和区间估计。
六、假设检验假设检验是一种通过样本推断总体特征是否符合某种假设的方法。
假设检验包括单样本检验、双样本检验等多种类型。
七、回归分析回归分析是一种通过建立数学模型来研究变量之间关系的方法。
回归分析包括简单线性回归、多元线性回归等多种类型。
八、实例应用1.医学领域在医学领域中,数理统计被广泛应用于临床试验、流行病学研究等方面。
例如,可以利用假设检验来判断某种药物是否有效,或者利用回归分析来研究某些因素对疾病发生的影响。
《应用数理统计》吴翊李永乐第二章-参数估计课后习题参考答案(总19页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第二章 参数估计课后习题参考答案设总体X 服从二项分布()n X X X p p N B ,,,,11,,21 <<为其子样,求N 及p 的矩法估计。
解:()()()p Np X D Np X E -==1,令()⎪⎩⎪⎨⎧-==p Np S Np X 12 解上述关于N 、p 的方程得:对容量为n 的子样,对密度函数22(),0(;)0,0x x f x x x ααααα⎧-⎪=⎨⎪≤≥⎩其中参数α的矩法估计。
解:122()()a E x xx dx ααα==-⎰2222()x x dx ααα=-⎰2321221333ααααααα=-=-= 所以 133a x α∧== 其中121,21(),,,n n x x x x x x x n=+++为n 个样本的观察值。
使用一测量仪器对同一值进行了12次独立测量,其结果为(单位:mm) ,,,,,⎪⎪⎩⎪⎪⎨⎧-=-==X S p S X X p X N 2221ˆˆˆ,,,,,试用矩法估计测量的真值和方差(设仪器无系统差)。
解:()()()∑∑====-====ni ini i S XX nX D X X n X E 12210255.014025.2321设子样,,,,,是来自具有密度函数()10,1,<<=βββx f 的总体,试用矩法估计总体均值、总体方差及参数β。
解:()()()()4.22ˆ2,1,407.012.1101221========-===⎰⎰∑∑==X Xdx xdx x xf X E x f XX n S X n X ni i ni i ββββββββ参数:总体方差:总体均值:设n X X X ,,,21 为()1N ,μ的一个字样,求参数μ的MLE ;又若总体为()21N σ,的MLE 。